Coercivity mechanism of La–Nd–Fe–B lms with Y spacer layer

Jun Ma(马俊), Xiao-Tian Zhao(赵晓天), Wei Liu(刘伟), Yang Li(李阳), Long Liu(刘龙),Xin-Guo Zhao(赵新国), and Zhi-Dong Zhang(张志东)

1Shenyang National Laboratory for Materials Science,Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,China

2School of Materials Science and Engineering,University of Science and Technology of China,Shenyang 110016,China

Keywords: La-Nd-(Y)-Fe-B films,magnetization reversal mechanisms,coercivity,multilayers

1.Introduction

The rare earth (RE) permanent magnet materials have been widely used in energy and information fields,[1-3]thus,it has caused a large amount of consumption of Pr, Nd and heavy RE,accompanied by the enrichment of high-abundance RE such as La/Ce/Y.[4,5]To make more efficient use of RE resources and reduce costs, high-abundance RE elements are gradually applied to the permanent magnet industry.[6,7]

However, the intrinsic magnetic properties of the main phase RE2Fe14B with high abundance of RE elements are far inferior to those of Pr2Fe14B and Nd2Fe14B.[8]For the Y element,within a certain range,the Y addition can improve the coercivity and the thermal stability of the magnet.[6,9]However, the excessive Y addition can lead to a significant attenuation of magnetic properties.[10]In magnetic films, tuning the magnetic properties can be achieved by constructing different multilayers structures.By introducing Nd/Nd-Cu/Ta interlayer into Nd-Fe-B multilayer films, the grain orientation and coupling state are improved to obtain high magnetic properties.[11-14]For the La-Nd-Fe-B system,the corresponding La-substituted Nd permanent magnet block is fabricated,and the results show that high saturation magnetization can be retained.[15]The isotropic films are also prepared,[16]the out-of-plane(OOP)preferred orientation thin film remains to be studied.For Y element,the main phase formation energy of Y is lower than that of La and Nd,[17]and it is more inclined to enter the main phase.[18]The effect of Y element on phase formation,structure,and magnetization reversal mechanism in La-Nd-Fe-B films remains to be further explored.

In this study,out-of-plane preferred orientation magnetic films of La-Nd-(Y)-Fe-B films were prepared by magnetron sputtering.The effects of a Y spacer layer on the phase formation,magnetic properties and magnetization reversal of La-Nd-(Y)-Fe-B films were investigated systematically.

2.Experiments and methods

Nominal composition (La0.3Nd0.7)16Fe72B12was chosen as the experimental target component and prepared by powder metallurgy.The sources materials used in the target are commercial with a purity of 99.99%.All the films were prepared by direct current (DC) magnetron sputtering.The films structures are as follows:Si (001)/Ta (40 nm)/(La0.3Nd0.7)16Fe72B12(150 nm)/Y(xnm)/(La0.3Nd0.6)16Fe72B12(150 nm)/Ta (40 nm),xis the thickness of Y, which is 0 nm, 10 nm, 20 nm, and 50 nm respectively.The four samples are named Y0, Y10, Y20, and Y50.Ta, as a buffer layer and covering layer, is a commercial target with a 99.95% purity.The base vacuum was 1.5×10-5Pa, and the sputtering atmosphere was Ar, and the pressure was maintained at 0.11 Pa.The sputtering rates of (La0.3Nd0.7)16Fe72B12and Ta targets were 4.72 A/s and 1.58 A/s, respectively.The substrate was heated and maintained at 500°C,and after depositing the Ta covering layer of 40 nm, the final films were obtained by annealing at 650°C for 20 min.

The magnetic hysteresis loops,the data for the micromagnetic analysis and FORC were all obtained by a superconducting quantum interferometer device (SQUID) (Quantum Design,San Diego,CA,USA).X-ray diffractometer(XRD)with Cuα1 radiation(λ=0.154056 nm)was applied to analyze the phases composition(Rigaku Smartlab D/Max 260).A ZEISS SUPRA 55 SAPPHIRE field-emission scanning electron microscope(FESEM)was used to analyze the element distribution.

3.Results and discussion

Figure 1 shows the hysteresis loops in the in-plane (IP)and OOP directions at 300 K.As the thickness of the spacer layer increases, theJvalues first decrease and then increase in the IP and OOP directions.The maximumJis 1.099 T of Y50 in the OOP direction.For the maximum magnetic energy product((BH)max),it also shows that as the thickness of the Y spacer layer increases,the value decreases first and then increases.The (BH)maxof Y10 is 7.02 MGOe, and those of the other three samples are all about 12 MGOe.The(BH)maxof Y0 and Y50 are basically the same.With increasing thickness of the Y spacer layer,the coercivities at 300 K are 1.14 T,1.36 T,0.952 T,and 0.614 T,respectively.Y10 has the maximum coercivity of 1.36 T, which is 20% higher than that of Y0(1.14 T).It can be seen that the Y spacer layer with different thickness has an effect on the coercivity of La-Nd-Fe-B films.For the four samples, there is perpendicular magnetic anisotropy (PMA) by comparing the difference OOP and IP loops.

Fig.1.Hysteresis loops of(a)Y0,(b)Y10,(c)Y20,and(d)Y50 samples in out-of-plane and in-plane directions at 300 K.

Figure 2 shows the demagnetization curves, coercivity,and saturation magnetization of the films at different temperatures.For Y10,the coercivity is 2.48 T at 150 K and 0.938 T at 380 K, which is higher than that of other samples at the same temperature.This also shows that a suitable thickness of Y spacer layer can improve the coercivity of La-Nd-Fe-B at temperature range of 150 K-380 K.Additionally, with increasing Y thickness, the saturation magnetization and remanence first decrease and then increase, which needs to be further explained.Meanwhile, the enhancement mechanism of coercivity remains to be further elaborated.

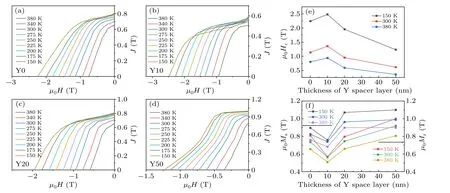
Fig.2.Demagnetization curves from 150 K to 380 K of(a)Y0, (b)Y10, (c)Y20, (d)Y50,(e)variation of coercivity, and(f)saturation magnetization and remanence with different thicknesses of Y spacer layer at different temperatures.

To explore the existing state of Y spacer layer in the film and its in uence on the phase formation of samples,the XRD patterns, SEM images, and the corresponding EDX mapping of Y element are shown in Fig.3.The diffraction peaks of the films are mainly from tetragonal RE2Fe14B phase.Due to the large atomic radius of La,[19]the main phase RE2Fe14B is instability, the La-B phase still presents in Fig.3(a).With increasing thickness of the spacer layer, the diffraction peak strength of La-B phase reaches a maximum at Y10, and then gradually decreases.The XRD data are used to semiquantitatively calculate the phase in the film,the results show that the proportion of La-B phase in the four samples increases first and then decreases with increasing thickness of the Y spacer layer, which corresponds to the trend of the saturation magnetization in Fig.2(f).The diffraction intensity of peak (006) has been consistently weakened after increasing the spacer layer thickness.On the one hand,the excessive RE will weaken the growth ofc-axis texture.[20]On the other hand,with increasing thickness of the Y spacer layer,Y further diffuses and the misaligned grains increase.The angles corresponding to the characteristic peaks(004),(105)and(006)of RE2Fe14B increase firstly and then decrease, the corresponding lattice size decreases first and then increases.By inspecting the relevant lattice parameterc/ashown in Fig.3(c),combined with the distribution of Y element in Figs.3(d)-3(f), it is concluded that the Y spacer layer diffuses and participates in the phase formation of the films.With the addition of Y spacer layer, in the initial stage, since Y has a smaller main phase formation energy than La, Y tends to replace La and participates in the formation of the main phase.Since La is replaced by Y, more La-B phases are formed.With further increasing the thickness of the Y spacer layer,more Y participates in the formation of the main phase.Due to the shrinkage effect of lanthanide elements,the atomic radius of Y is smaller than that of La,the lattice size is reduced,and the stability of the main phase is increased,so that La can further participate in the formation of the main phase,which is similar to the results of La-Ce co-doping in Nd2Fe14B,[21]corresponding to the decrease of the proportion of La-B phase.In conclusion,the Y spacer layer can participate in the formation of the main phase without significantly changing thec-axis orientation of the film, and plays an important role in regulating the formation of the La-B phase.

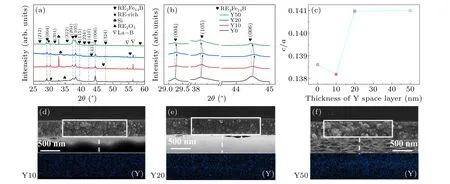
Fig.3.(a)XRD patterns of Y0, Y10, Y20, and Y50, (b)enlarged XRD patterns for(004), (105)and(006)characteristic peaks of RE2Fe14B,(c)the dependence of lattice parameter c/a of 2:14:1 tetragonal phase on thickness of Y spacer layer,(d)-(f)the cross-sectional SEM images of different Y spacer layer thicknesses and the corresponding EDX mapping of the element Y taken from the white rectangular region.

In order to better understand the effect of Y spacer layer on the coercivity,the coercivity mechanism is fitted by micromagnetic theory[23,24]using the magnetic parameters in Fig.2 and the parameters in related reports.For the micromagnetic theory, when the coercivity mechanism is dominated by nucleation mechanism,it can be handled with the following formula:

whereHc,Ha,Neff, andMsare coercivity, anisotropy field,effective local demagnetization factor, and saturation magnetization,respectively.The data ofHaof La2Fe14B,Nd2Fe14B,and Y2Fe14B are obtained from related reports.[8]And the anisotropy fields are averaged based on the atomic ratio of RE elements in the targets.Neffdefined as the local effective demagnetization factor is a microstructural coefficient,which describes the demagnetization effect of grain surfaces and volume charges.αis the microstructure parameter in the actual magnet,α=αKαφ; the coefficientαφis related to the crystal grains deviating from thec-axis,expressing the decrease in the nucleation field caused by misaligned crystal grains;αKis related to the non-uniform defect region,indicating a decrease in the nucleation field due to the grain damage on the surface of the magnet and the imperfect internal grain.αKandαφcan be expressed by the following formulas:

whereφis the angle between the external field and thec-axis,δB, ΔK,A, andr0are defined as the width of Bloch domain wall,the reduction of magneto-crystalline anisotropy constant in defect region,the exchange constant,and the half width of the planar defect region, respectively.In micromagnetic theory, whenαK＞0.3, the coercivity mechanism should be a nucleation mechanism;whenαK＜0.3,the coercivity may be determined by pinning mechanism or by nucleation mechanism.Typically,the nucleation mechanism is considered in the following two situations:[23,25]considering the uniform magnetization inversion, the results are shown in Figs.4(a)-4(d),however the fitting magnetic parameters are not within a reasonable range (0＜αK＜1), and the linear fitting interval is narrow.Considering that the magnetic particles are strongly coupled and the anisotropy axis is not strictly along thec-axis,one reversed magnetic moment would lead to the joint reversal of the surrounding magnetic moments,based on this case,αφ=αminφ, the fitting results are demonstrated in Figs.4(e)-4(h).The values ofαKare 0.761, 0.770, 0.732, and 0.523,respectively, indicating that the nucleation mechanism is the dominant mechanism of the coercivity of the four films.At the same time,the values ofNeffobtained by fitting are 1.41,1.33,1.29, and 0.923.For Y10, the values ofαKandNefftogether make it obtain high coercivity.Therefore, the fit parameters are in a reasonable range, with a linear temperature range of 200 K-380 K,the coercivity in the four films is dominated by nucleation mechanism.In short, the coercivity mechanisms are deeply dominated by the nucleation mechanism.Moreover,with increasing thickness of the Y spacer layer,αKfirst increases and then decreases, whileNeffis decreasing, which together make the coercivity of Y10 greater than that of Y0.

Fig.4.(a)-(d)Plots of Hc/Ms versus Ha/Ms for Y0,Y10,Y20,and Y50 for testing the nucleation mechanism where the magnetization process is uniform,(e)-(h)the plots of Hc/Ms versus αminφ Ha/Ms to test the nucleation mechanism taking the in uence of misaligned grains into account.

For FORC method, the magnetization of the sample is first saturated, then the external magnetic field is reduced to the reversal field (Hr), and then the field measurement is carried out fromHrto saturation field.In this way, hundreds of minor loops can be obtained to form the FORC diagram.And the magnetization isM(H,Hr)(H ≥Hr), whereHis the applied magnetic field.The FORC distribution parameter is defined as[26-28]

The magnetization reversal processes of the films are further studied by the FORC method.Figure 5 shows the corresponding FORC graph of the four samples at 300 K.The left side of the graph shows the normalized FORC, and the graphs in the middle are the corresponding contour graphs in their own graphics.The distribution ofρ=0 indicates that the magnetization process is reversible.The distribution ofρ ̸=0 indicates that the magnetization process is irreversible.[29]All the samples start irreversible magnetization process from their corresponding point 1; andρreaches a maximum at point 2;at point 3,ρgradually goes to the plane ofρ=0.Y10 has the largest initial field of the irreversible inversion in the four samples, which is-0.75 T, indicating that its magnetic moment is not easily reversed.In all films, the non-zero tailing pairs appear in the magnetic field after point 3, corresponding to the characteristics of nucleation mechanism,[30]which is consistent with the previous fitting results by the micromagnetic theory.

FORC method can be used to characterize the magnetic interaction and coercivity distribution by transforming the coordinate system as follows:

In this coordinate system, the distribution of peak alongµ0Hc＞0 represents the distribution of coercivity,without considering the interaction between particles.And theµ0Hurepresents the distribution of mean interaction filed.[31]Along the direction ofµ0Huaxis,whenρmaxis distributed in the positive direction ofµ0Hu,the average interaction is dipole interaction,otherwise, it is the exchange interaction.The related results are shown in Figs.6(i)-6(l), and the distribution of coercivity also corresponds to the coercivity at room temperature in Fig.1.In Y10, the coercivity distribution of the film is more concentrated.For the magnetic interaction between particles,the positions ofρmaxshow that dipole interaction dominates in all the samples,which increases firstly and then decreases,and Y10 has the largest dipole interaction, indicating that the exchange interaction in the film also correspondingly reduces and therefore the coercivity of Y10 increases.So, the high dipole interaction of the Y10 sample can serve as a new reason to explain its high coercivity.

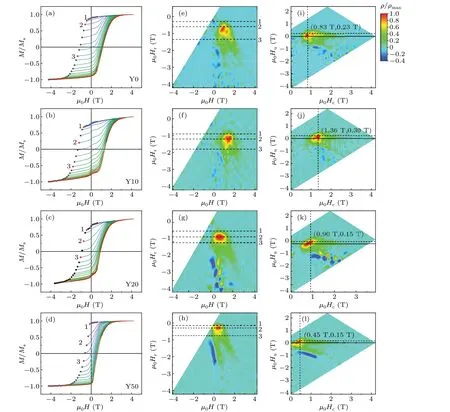
Fig.5.(a)-(d) FORCs (normalized to 1) along out-of-plane direction of the four films, (e)-(h) corresponding contour plots distribution in theµ0Hr-µ0H coordination,and(i)-(l)FORCs distribution in theµ0Hb-µ0Hc coordination of films Y0,Y10,Y20,and Y50,respectively.

4.Conclusion

In summary,in La-Nd-Fe-B films,with increasing thickness of the Y spacer layer, Y can regulate the formation of La-B phase.Combined with the results of micromagnetic fitting and FORC, it can be determined that all the samples are dominated by the nucleation mechanism.Magnetic interactions in the thin films are also dominated by the dipole interaction.Due to thec-axis preferred orientation,good magnetic microstructure parameters and dipole interaction,Y10 has the highest coercivity at 150 K-380 K.All the results are beneficial for understanding the coercivity mechanism and magnetization process of permanent magnets with Y.

Acknowledgments

Project supported by the National Key Research and Development Program of China (Grant No.2021YFB3500303)and the National Natural Science Foundation of China(Grant Nos.52031014 and 51971219).