灰狼算法优化SVR的10kV配网线损率预测研究

杨正宇,沈志强,郑成源

(1.云南电力试验研究院(集团)有限公司,云南 昆明 650217;2.云南电网有限责任公司临沧供电局,云南 临沧 677000;3.云南电网有限责任公司电力科学研究院,云南 昆明 650217)

0 引 言

电网的线损率是一个综合性、全面性的评价指标,其不仅可以反映一个单位或一个区域的供电经济性,也可以间接反映供电的技术条件和管理水平[1]。有效控制线损率、降低线路损耗、实现电网经济运行是电力企业现代化管理的核心内容[2],因此,对线损率进行准确预测,及时对高损线路进行巡检维护,有利于降低供电成本,保证电网经济稳定地运行。

近几年来,有关配电网线损、线损率的计算与预测研究变得愈发活跃[3-7]。传统常用的统计线损的理论计算方法有均方根电流法、平均电流法等。虽然线损的理论计算在一定条件下能够取得较好的效果,但是由于理论计算条件较为理想,现实中部分电力数据较难获取等问题,实际来说并不具有代表性。随着计算机、人工智能技术的发展及其在电力系统中的运用,许多新的方法被用于线损计算中[8-9]。

该文以10 kV配电网运行数据为基础,对原始数据进行必要的预处理操作,以马氏距离为异常值的判定标准,采用卡方分布确定异常阈值,对原始数据中的异常值进行剔除,为下文的建模分析打下基础。然后通过主成分分析对所选特征进行降维处理,利用灰狼优化算法具有强搜索性、强遍历性的优点与支持向量机回归模型相结合,对支持向量机回归模型的惩罚因子c和核函数g进行优化[10-11]。之后将处理好的特征量作为输入建立模型,最终通过云南电网某供电所真实电力数据对模型的预测效果进行验证。

1 GWO-SVR模型数学理论

1.1 支持向量机回归

相比于约束较为严格的SVM分类,回归则比较宽松[12-13]。对于回归问题,给定训练数据D={(x1,y1),(x2,y2),…,(xm,ym)},需要构建一条以f(x)为中心,宽度为2ε的隔离带,当训练样本落入此隔离带时,认为预测是正确的,即仅当f(x)与y之间的差异绝对值大于ε时才计算损失。在图1中,认为落入两条虚线中的样本残差为零,也就是它们的误差是可以容忍的。需要做的就是找到这两条合适的虚线边界,目的是使在虚线外的样本到虚线的直线距离ζ最小,最后再对区域外的点进行回归,其中损失函数如式1所示：

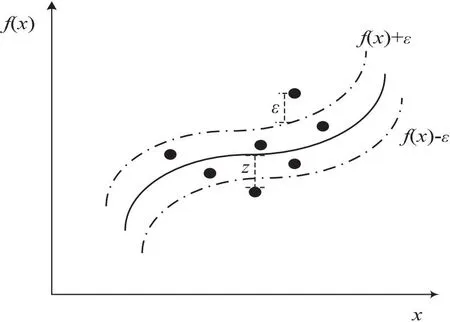
图1 支持向量机回归原理

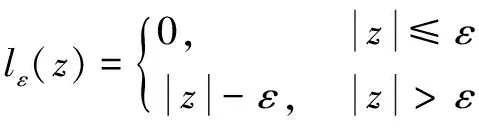
(1)

式中：z为数据点到f(x)的距离;ε为误差阈值。

s.t.f(xi)-yi≤ε+ξi

(2)

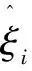
在此基础上引入拉格朗日乘子并对其求偏导,并将结果带入SVR对偶问题,可得出SVR解的公式为：

(3)

径向基核函数(RBF)是常用的核函数,其函数表达式为：

K(xi,xj)=exp(-r‖xi-xj‖2),r>0

(4)

式中：r为函数的宽度参数,控制了函数的径向作用范围。

1.2 灰狼优化算法的数学描述

在灰狼优化算法中,狼群中每一头灰狼代表了种群的一个潜在解。为了描述灰狼的社会等级,将α狼的位置视为最优解;将β和δ狼的位置分别作为优解和次优解;w狼的位置作为其余的候选解。在GWO算法中,由α,β,δ引导狼群搜索,而w跟随前面的3种狼。灰狼优化算法的原理如图2所示。

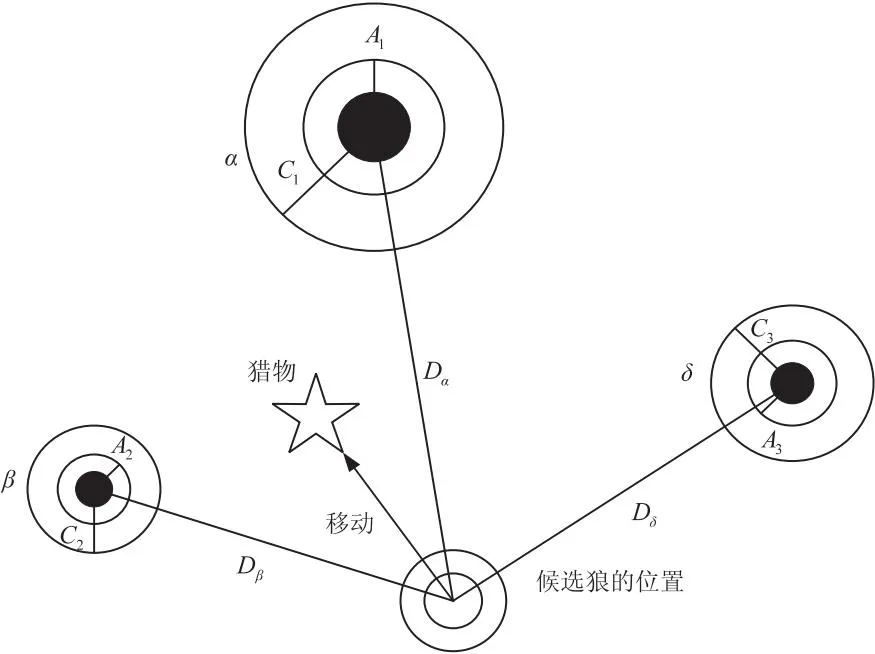
图2 灰狼优化算法原理

灰狼狩猎时需要包围猎物,包围的数学描述为：

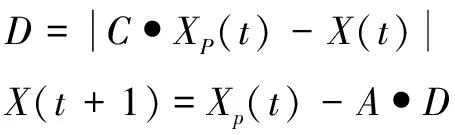
(5)

式中：t为当前迭代次数;A和C为协同系数向量;XP为猎物的位置;X为灰狼的位置。该文引入一种随迭代次数增加而线性变化的收敛因子α,向量A和C与收敛因子α的计算方式如下：

(6)

式中：α的分量在迭代过程中从2线性减少到0,it为当前的迭代次数,Maxit为设置的最大迭代次数,r1,r2是[0,1]之间的随机向量。

在狩猎阶段中狩猎通常由α狼引导,β和δ也可能偶尔参与狩猎行为,在每次迭代过程中,保留迄今为止获得的最优的三个解(α,β,δ的位置),迫使其他狼(w)根据最优的搜索位置采用以下公式对它们的位置进行更新：

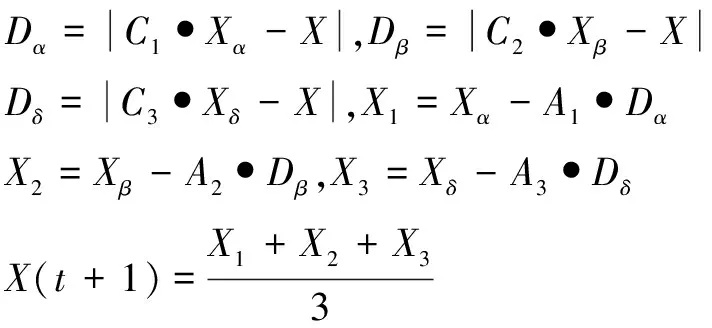
(7)

式中：Dα,Dβ,Dδ分别表示当前候选灰狼与最优三条狼之间的距离,C1,C2,C3,A1,A2,A3皆为系数向量,Xα,Xβ,Xδ分别为三种狼的原始位置,X1,X2,X3分别为三种狼更新后的位置。

为了描述接近猎物,根据式6,通过逐渐减少α的值,A的值也随之波动。当A的随机值在[-1,1]中时,搜索狼可以是候选狼的当前位置和猎物之间的任何位置。灰狼主要根据α,β和δ狼的位置搜索,为了模拟搜索的分散性,利用A大于1或A小于-1的随机值来迫使搜索狼远离猎物,这样会使GWO算法强调勘探,更有利于全局搜索。

1.3 GWO-SVR预测模型

基于GWO-SVR的线损率预测流程包括数据预处理、初始化种群、灰狼位置寻优等过程,具体步骤如下：

(1)数据预处理：对数据的预处理环节是分析研究的首要步骤,包括缺失值填补、异常值分析删减等操作,同时利用PCA对原始数据进行降维处理。

(2)设定算法初始值：此处所需设定的参数包括种群规模、最大迭代次数、数据维度以及SVR中核函数g以及惩罚因子c(取值范围)。

(3)模型中导入训练集数据,初始化种群,以适应度作为评价函数值,不断更新灰狼的位置信息,寻找参数最优的灰狼坐标。

(4)以最大迭代次数为运行的截止条件,当运行次数达到设定值后,得到支持向量机回归最优参数,代入回归预测模型。

(5)模型中导入测试集数据,利用相应指标对模型的预测效果进行评价。

GWO算法优化SVR模型的流程如图3所示。

图3 GWO算法优化SVR模型流程

2 数据预处理

2.1 基于马氏距离的异常值检验

在所获取的真实电力数据中,一般来说会存在数据重复以及数据缺失的情况,若不经过数据的清洗而直接使用的话效果往往会适得其反。该文采用“热卡填充法”对原始数据中的缺失值进行填补,对于离群值采用删除相应值并采用缺失值的填补办法对其值进行修正处理。所收集的数据特征如表1所示。

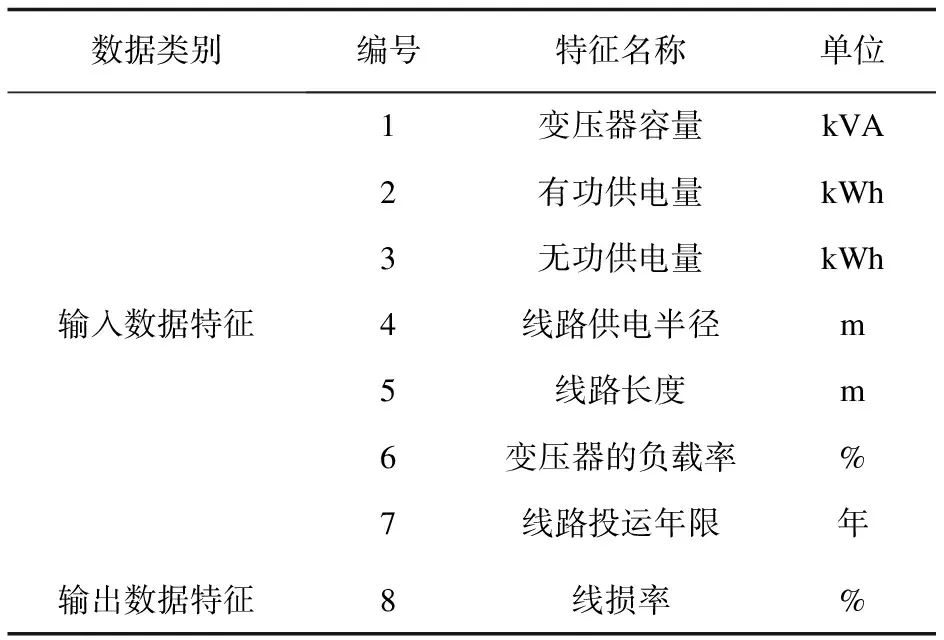
表1 模型输入输出特征类型

与目前常用的聚类方法欧氏距离不同,马氏距离可以应对高维线性分布的数据中各维度间非独立、同分布的问题[14]。对于一个均值为μ=(μ1,μ2,…,μp)T,协方差矩阵为Σ的多变量矢量x=(x1,x2,…,xp)T,其马氏距离为：

(8)

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量：

(9)

该文所采用的数据均来自云南电网某供电所,共涉及10条10 kV配电线路共计1 200组电力数据,根据置信水平α=0.95对应卡方分布置信区间,以输入特征量确定检验的自由度为7(输入模型的特征个数),通过卡方分布计算可得卡方检验阈值为14.07。由于马氏距离服从卡方分布,笔者认为马氏距离大于14.07的数据即为异常值并予以剔除,达到提高样本质量的目的。基于马氏距离的异常样本检测的结果示意图如图4所示。

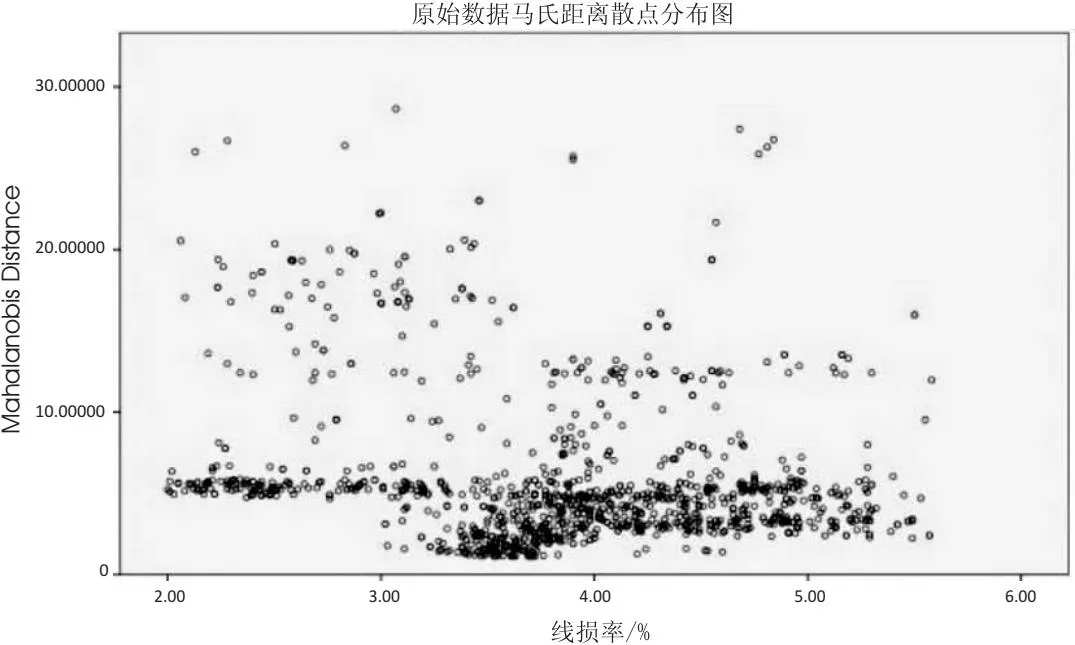
图4 马氏距离的异常样本检测的结果

2.2 数据降维处理

数据降维具有减少数据维度和需要的存储空间、节约模型训练计算时间、去掉冗余变量,提高算法的准确度等优点[15-16],其通过一定的手段和方法,降维重组成一组新的维度较少的主成分综合指标,作为替代指标中原本的主成分数据集。表2给出了实际线损率数据经过 PCA 算法处理之后的前4个主成分的特征占比累计贡献率。

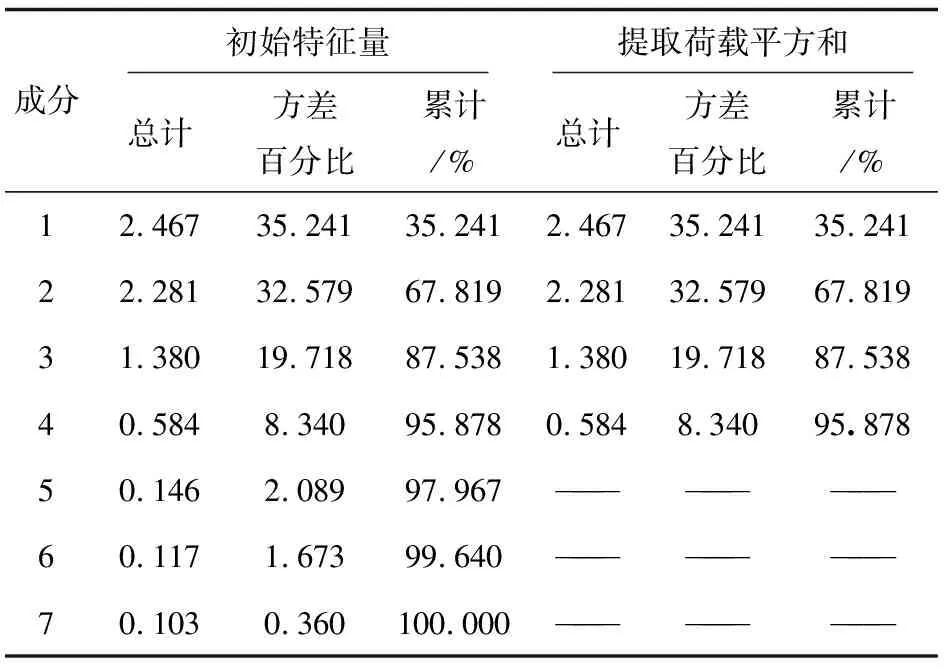
表2 总方差解释

PCA处理之后原始数据被重新组合成新的互不相关的特征量。由表2可知,前4个主成分的累计特征占比为95.878%,大于90%,也就是说明原始数据中绝大部分有效信息被成功提取。因此,选用这4个新的主成分数据来对原来所选的7维数据进行替代。经过数据重构后的主成分因子荷载如表3所示。

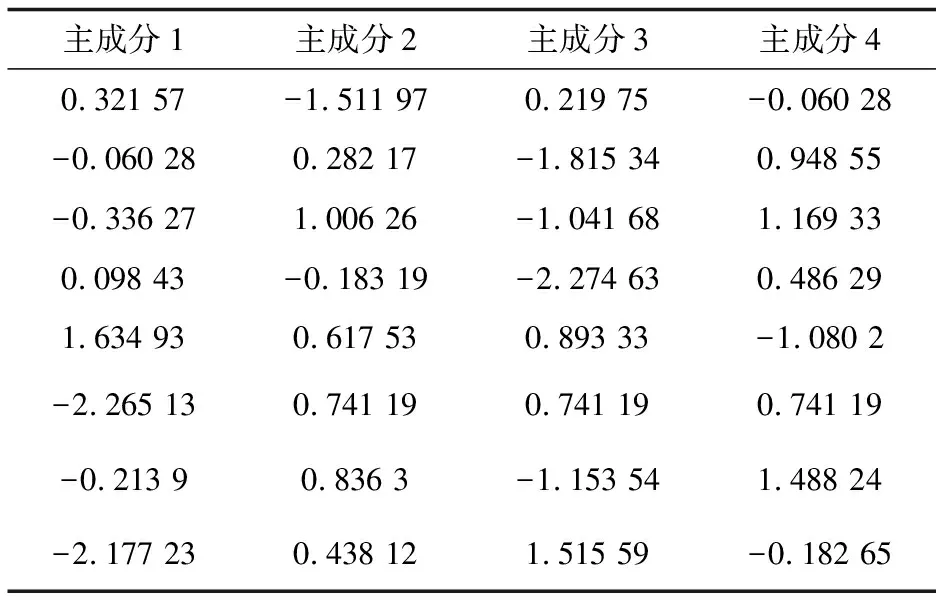
表3 主成分因子荷载

2.3 GWO-SVR预测模型初始参数的选择

SVR模型具有能处理高维非线性问题的优点,但是相应的运算和存储量都会有很大的消耗。在群智能优化算法中,种群数量的取值一般为20～40,粒子数量越多,搜索范围越大,越容易找到全局最优解,但相应的算法运行时间也越长。为了保证模型的运算效率,该文初始种群规模选择20,并且限制迭代次数最大为100代。

在支持向量机模型中,当所选参数趋于无穷大时,代表着不允许出现分类误差的样本存在,因为这将是一个过拟合问题,当所选参数趋于0时,不再关注分类是否正确,只要求间隔越大越好,那么将无法得到有意义的解且算法不会收敛。因此,灰狼优化算法针对的目标即SVR模型的参数(惩罚因子c和核函数g)需要在运算中给予限制,文中设定参数的取值范围在0.01至100之间。

文中初始数据设定情况如表4所示。

表4 算法初始化参数设定

3 实验结果及分析

3.1 预测模型评价指标

常用的评价指标包括均方根误差、平均绝对误差和相对误差,其计算方式如下所示：

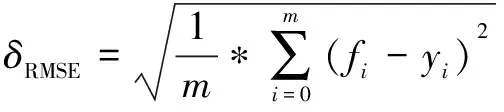
(10)

(11)

δ=(fi-yi)*100%

(12)

式中,m代表数据集的样本总量,fi和yi分别代表真实值和预测值。在模型运算结果的分析中,经常使用上述指标来评价所建立模型的优劣程度,预测结果的评价指标越小,说明测试集的预测精度越准确,也从侧面反映了所建模型是理想的。因此,将上述的评价指标用于之后的预测模型的性能评价之中。

3.2 基于支持向量机回归的线损率预测结果分析

文中使用留出法(Hold-Out)以8∶2的比例划分训练集以及测试集。经过支持向量机回归所得到的预测结果如图5所示。

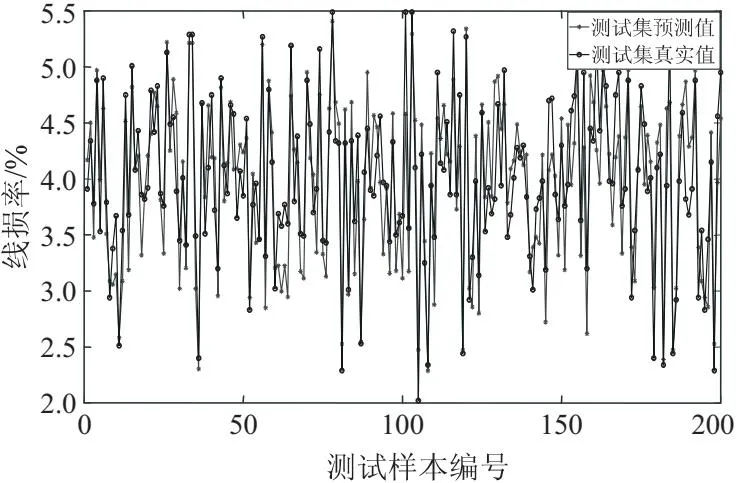
图5 SVR模型预测值与真实值对比

通过图5可以看出,图中两条线分别代表线损率测试集的预测值以及真实值,在图中两线表现出重合度忽高忽低的画面,说明所建立的SVR模型虽然能在一定程度上对线损率进行预测,但是预测性能还有待提高。为了进一步描述模型的预测性能,文章引入了预测残差以及相对误差,如图6和图7所示。通过预测残差可以看出,在模型的预测过程中线损率残差虽然围绕0值上下波动,但是部分测试样本的波动范围过大,相对误差表现出其最大相对误差为27.4%。通过利用上述所建立的评价指标计算可知,支持向量机回归预测模型的均方根误差为0.389 1,平均绝对误差为0.330 5。

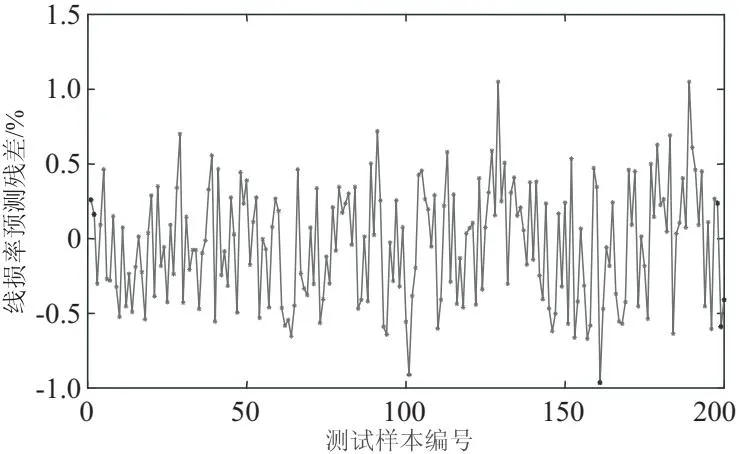
图6 SVR模型预测残差

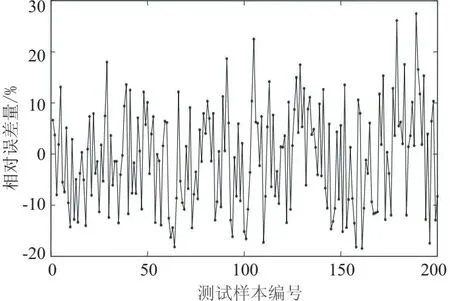
图7 SVR模型预测相对误差

3.3 灰狼算法优化支持向量机的线损率预测

文中选用均方误差作为优化的适应度函数值,其适应度函数(目标函数值)如式13所示：

(13)

式中,m代表数据集的样本总量,yi和yj分别是真实值和预测值,适应度值越小说明模型的拟合程度越高。根据表4所设定参数对模型赋予初值,经过10次仿真运算求平均得到模型的适应度曲线如图8所示。

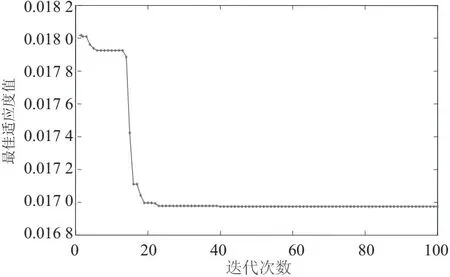
图8 GWO-SVR模型适应度曲线

由图8可以看出,在迭代次数设置为100次的情况下,模型经过20次搜索就能达到一个最优值附近,同时在搜索前期经过少数几次搜索就能寻找到更优的值,逐渐向最优值逼近,体现了灰狼优化算法的搜索性强,搜索范围广且利于跳出局部最优的优点,这也满足在模型建立时低成本、省时间的要求。使用GWO-SVR模型对实际线损率测试集数据进行仿真的结果如图9所示。

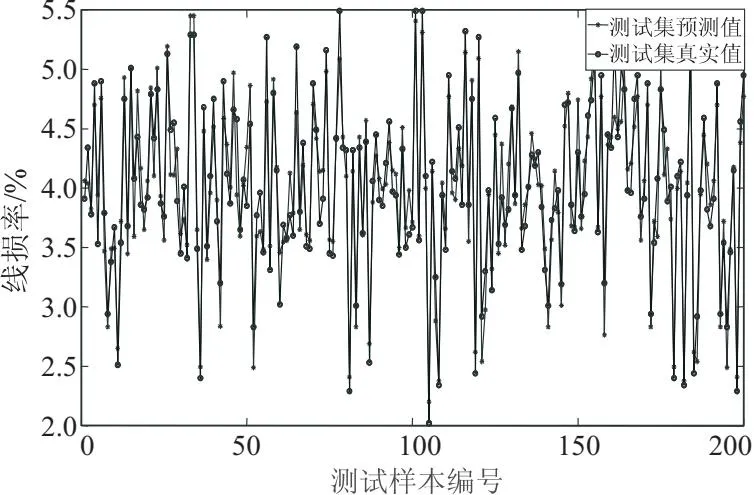
图9 GWO-SVR模型预测值与真实值对比

如图9所示,将GWO-SVR的线损率预测结果可视化,在200个测试集样本进行测试过程中,可以看到在样本实际测试的过程中的折线图基本重合,代表着预测值与实际值较为接近。图10为测试数据的残差,可看出测试数据的残差值围绕0上下波动,且大多数预测残差都在0值附近,说明预测的效果较为理想。根据上文所提及的评价指标来看,预测模型均方根误差为0.233 2,平均绝对误差为0.195 8。图11为预测模型的相对误差,图中显示最大的相对误差为14.4%,相对于原本的支持向量机模型来说,GWO-SVR模型具有更优异的预测性能,均方根误差与平均绝对误差相对于单一的SVR模型分别降低了0.155 9和0.134 7,并且最大相对误差都在15%以内。

图10 GWO-SVR模型预测残差

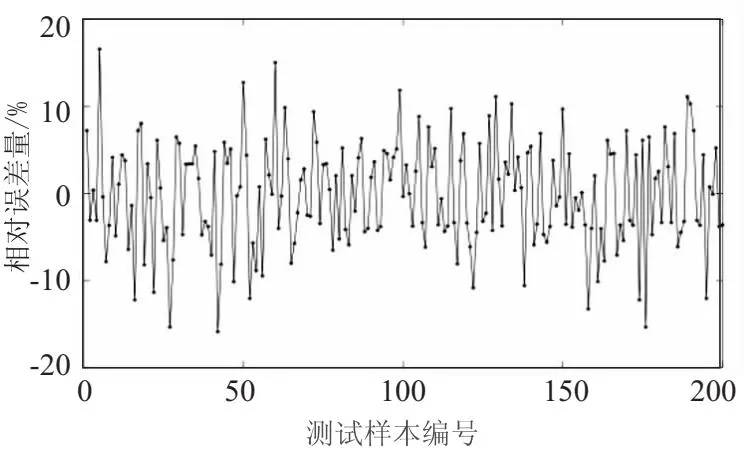
图11 GWO-SVR模型预测相对误差

为了验证文中模型在10 kV配电网线损率预测方面的优异性能,表5为该模型与传统预测模型SVR、BP神经网络、ABC-SVR对于同一样本的预测结果比较,可以看出GWO-SVR模型具有最高的预测精度以及最快的运算速率。

表5 各模型运算结果对比

4 结束语

提出基于灰狼算法优化支持向量机回归的10 kV配电网线损率预测方法,利用主成分分析法对经过预处理之后的数据进行降维,在提取数据有效信息的情况下减少模型的复杂程度,最终利用灰狼优化算法对支持向量机回归的惩罚因子c和核函数g进行优化。通过仿真实验,绘制出模型的预测值与实际值的对比图,最后从模型的评价指标出发,对比文中4类模型对于10 kV配电网线损率的预测性能,验证了所建立的模型在10 kV配电网线损率预测方面的有效性。