基于交互基函数的数据流聚类算法研究

黄承宁,李 莉,姜丽莉,徐平平

(1.南京工业大学浦江学院,江苏 南京 211222;2.东南大学 信息科学与工程学院,江苏 南京 210096)

0 引 言

数据流是一种潜在的海量、连续、快速的数据信息序列,引起了数据挖掘领域的极大关注和研究热潮[1]。在人类生活的各个方面都存在数据流,如网络媒体传输的监测信息、煤矿传感器传输的信息、网站信息、金融和证券公司产生的经济信息、天气预报信息等。由于这种形式的数据海量且实时更新,传统的聚类方法无法对其进行处理,因此迫切需要新的聚类方法[2]。目前,已经有很多数据流聚类方法被提出,不过均根据传统数据的聚类算法扩展而来,且均没有考虑到特征之间的关系。

该文提出将交互基函数(IBFs)引入数据流聚类,结合模糊ART算法,考虑特征的自交互与交叉交互,以相对较低的计算成本生成灵活决策边界来找到最优聚簇,实现了聚类高精度与低错误率,提高了算法的数据流聚类质量。

1 数据流聚类与自适应谐振理论

1.1 数据流聚类

数据流具有内在的特性,包括无限大小、时间顺序和动态变化。与传统的数据挖掘相比,数据流挖掘只是在满足单次通过、实时响应、有界内存和概念漂移检测等约束条件下产生近似结果。

数据流(DS)定义为数据对象或样本序列或为一个带有时间戳(Time Stamp)的多维数据点集合：DS={x1,x2,…,xn},其中xn为第n个到达的数据对象(实际应用中n的取值可以为无限大[3-4])。其中每个数据点是一个d维的数据记录,其到达时间为ti。

数据流聚类将DS中的相似对象划分为一个或多个组(称为“簇”,Cluster),划分后,同一簇中的元素彼此相似,但相异于其他簇中的元素。

针对高维、动态、实时的特点,目前不少研究者都已经提出了许多有效的数据流聚类算法,但数据流信息是不确定的,总是存在离群点且包含噪声[5],传统的聚类方法无法对其进行处理,因此发现新的数据流聚类方法越来越迫切。

目前从实际应用看,数据流聚类基本都面临着许多共性问题[6-7]：(1)内存有限：数据流中的数量往往是庞大的,不可能在内存和硬盘中存储整个数据流;(2)一次扫描：因为巨大的数据量,传统的扫描方法不再适用,在对数据的访问只能单次线性,也就是只按顺序依次读取一次,不能进行随机访问;(3)实时响应：大多数应用程序要求快速响应,因此挖掘应该是一个连续的在线过程;(4)概念漂移：数据分布经常随时间变化。目前典型的数据流聚类算法包括REPSTREAM,ACSC,G-Stream,MR-Stream,CellTree以及RPGStream等[8]。

1.2 自适应谐振理论

自适应谐振理论(ART)[9]是一种学习模型,它模拟人脑捕获,识别和记忆有关对象和事件的信息,既是一种认知理论,也是一种关于大脑如何在不断变化的世界中快速学会分类、识别和预测物体和事件的神经理论。该文提出的算法便是在模糊自适应谐振理论基础上引入交互基函数(IBFs)[10]扩展进行数据流聚类,从而提升聚类精度与质量。

模糊自适应谐振理论的体系结构由用于接收输入模式的输入层F1和用于聚类的类别层F2组成[11],如图1所示,输入层F1包含的输入向量被提交到网络,与识别层F2中各个类簇的权值向量进行相似度比较并归类。

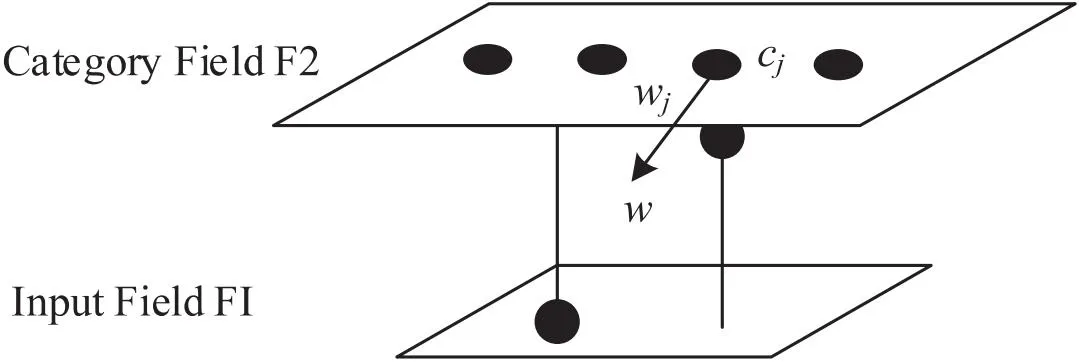
图1 模糊ART结构

模糊ART使用模糊算法并引入一个“补编码”[12]来解决“类别扩散”问题。模糊ART执行步骤如下：

(1)类别选择：对于每个输入模式I,模糊ART根据选择函数为识别层F2中的每个聚簇计算一个选择值,并标识具有最大值的聚簇为获胜聚簇,第j个簇的选择函数定义为：

(1)

(2)模板匹配：使用匹配函数Mj*评估输入模式I与获胜聚簇Cj*之间的相似性,该函数定义为：

(2)

如果获胜聚簇Cj*满足警戒标准Mj*≥ρ,会发生谐振,从而导致步骤3的中心学习。否则,将在其余聚类中选择新的获胜聚簇。如果没有获胜聚簇满足警戒标准,则将生成一个新的聚簇来对输入模式进行编码。

(3)中心学习：如果Cj*满足警戒标准,其对应的权重向量Wj*将通过函数进行更新,定义为：

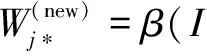
(3)

模糊ART中基于警戒准则计算的簇的VR是由特征空间中与簇关联的区域几何定义的,它从几何上解释了模糊ART的警戒准则,认为落入VR的输入模式与相应的簇相似,而VR的形状和功能行为则取决于补编码的使用[13]。

2 基于交互基函数的数据流聚类

2.1 交互基函数

如前所述,用于训练的特征构成了问题的基础向量。例如,当特征数量p=2时,搜索空间是由特征的正交轴形成的平面,每个特征都是一个基向量。三个特征形成三维基础,以此类推。如果把一个特征看作一个基向量,基函数就是一个变换。在最简单的情况下,基函数可以是等式：

f(X)=X

(4)

多项式函数的一个特殊情况,即当a=1：

f(X)=Xa

(5)

f(X)=(1-X)a

(6)

也可以定义其它基函数,例如指数：

f(X)=(eX)a

(7)

回归分析中常用的是基函数,它们具有改变回归平面性质的作用。例如,从恒等式到变量的平方的转换具有将回归线变为抛物线的效果。但DTs(决策树)[14]中基函数的使用并没有同样的效果。考虑K个实函数bi的一般情况：R→R,i=1,2,…,K,称{f1,f2,…,fK}为一组基函数。然后利用基函数得到的T个新特征扩充p个特征集：

X*=(X1,…,Xp,Xp+1,…,Xp+T)

(8)

并且X*∈RP+T,Xp+i=fsi(Xji),i=1,2,…,T,si∈{1,2,…,K},ji∈{1,2,…,p}。

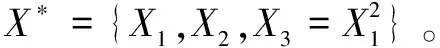
由于基函数在原基中仍然产生正交划分,笔者的建议是在构造X*时使用两个或多个特征之间的交互信息。这些交互不同于自交互,可以通过一组D函数来识别,这些M函数通过基函数来再现特征变换的功能交互,这些交互函数被定义为：

hhi：Rpk→Rh

(9)

(b1(X1),b1(X2),…,bk(Xp))

(10)

此设置下,定义：

X*=(X1,…,Xp,Xp+1,…,Xp+D)

(11)

Xp+i=hi(b1(X1),b1(X2),…,bk(Xp))
i=1,2,…,D

(12)

通过将标准递归划分方法应用X*上,并考虑到特征之间的相互作用,在X上的投影将提供一个斜划分(最终也可能是非线性的)。

IBFs提供的框架不仅允许诱导出斜划分,还允许诱导出非线性决策边界[16-17]。这是通过在数据集中特征生成的子空间X=(X1,X2,…,Xp)中投影方程hi(b1(X1),b1(X2),…,bk(Xp))=a来完成的。

2.2 基于交互基函数的数据流聚类算法

基于交互基函数的特性,在实验中将IBFs引入模糊ART,提出IBFs_ART算法,用于对数据流进行聚类。通过对原始输入特征进行分数阶变换,诱导出单一的超参数,在实现上比模糊ART更具灵活性,且进一步提升聚类精度。

IBFs_ART算法通过分数阶交互基函数(IBFs)对模糊ART进行了扩展,提出了一种新的生成柔性决策边界的策略。目标是评估IBFs在IBFs_ART中的表现。当样本x={x1,x2,…,xd}即将到来时,每个特征在[0,1]中被归一化。对于IBFs,用d个新特征来扩大d个特征的集合：

x*=(x1,x2,…,xd,xd+1,xd+2,…,x2d)

(13)

其中,使用自交互时x*∈R2d,xd+j=fp(xj),p∈{1,2,…,K}。使用交叉交互时xd+j=g1(f1(x1),f2(x2),…,fK(xd))。

考虑如下函数：

f1(xj)=(xj)a

(14)

f2(xj)=(1-xj)a

(15)

f3(xj)=(exj)a

(16)

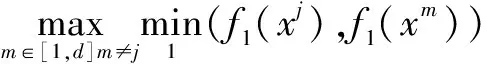
(17)

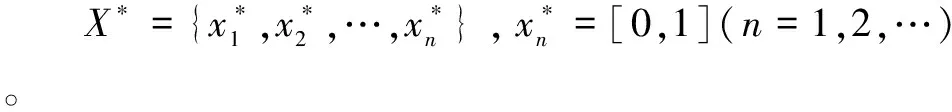
IBFs_ART算法如下所示：

输入：DS={x1,x2,…,xn}

输出：节点集合C={c1,c2,…,cn}和权值W={Wc1,Wc2,…,Wcn}

(1)：for eachxn

(4)：使用公式1计算选择函数,求出活动节点Λ(Λ∈C)

(5)：从活动节点中查找获胜聚簇J：J=argj∈Λmax(Tj)

(6)：使用公式2计算匹配函数;

(7)：if获胜聚簇J满足Mj≥ρ

(8)：使用学习函数(3)更新获胜聚簇J

(9)：else

(10)：类别J：Λ←Λ-J

(11)：if活动节点Λ≠∅then

(12)：返回执行第5步

(13)：else

(14)：J=|C|+1

(15)：创建新的聚类：C←C∪J

(16)：初始化新的聚类：wj=I

(17)：end if

(18)：end if

(19)：end if

3 实验与结果

3.1 实验环境

本次实验计算机配置为Inter Core i7-7500U 2.90 GHz处理器和4 GB内存,Windows10 操作系统,所有比较程序均在MATLAB上设计和运行。

3.1.1 数据集

为了对聚类的有效性进行更好的评价,在实验中采用了人工数据集和真实数据集,见表1。

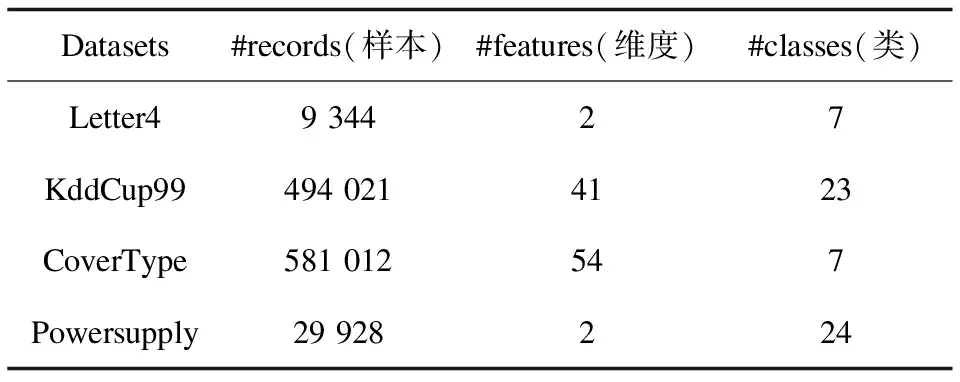
表1 数据集

Letter4由Java代码https：//github.com/feldob/生成。它包括9 344个样本,2个维度和7个类。

KddCup99来源于林肯实验室的一项入侵检测评估项目,仿真各种不同的用户类型、网络流量和攻击手段,记录了9周内TCP网络连接和系统审计数据。包含约50万条连接记录,这些记录含1种正常的标识类型和22种训练攻击类型,共有23个类,每个连接记录包含41个维度。

CoverType来源于某国家森林的四片荒野区域的观测。共包含581 012条记录,分为7种类型,每条观测记录包含54个维度。

Powersupply来源于意大利某电力公司的供电数据,记录两个电能：来自主电网的电能和来自其他电网的电能。该流包含2015年至2018年三年供电记录。数据变化主要来自季节、天气、一天的时间(例如早晚),以及工作日和周末的差异。它由29 928个样本,2个维度,24个类组成。

3.1.2 聚类评价指标

为了评价算法性能,引入了三种评价指标：

(1)Accuracy(purity)。

(18)

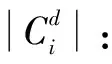
(2)NMI(normalized mutual information)。

NMI是一个量化两个分布之间共享的统计信息的对称度量,当类簇标签和样本类别之间存在一对一的映射时,NMI值达到最大为1.0。A为真实聚簇A={A1,A2,…,Ak},B为通过某个聚类算法得到的聚簇B={B1,B2,…,Bh},C为混淆矩阵,C中的元素Cij表示既在A中又在B中的样本个数。

(19)

其中,CA(CB)为聚簇A,B同时在矩阵C中的簇数目,Ci.(C.j)为C中第i行的元素和;N为样本个数。

(3)RI(rand index)。

RI(兰德指数)的计算公式为：

(20)

3.2 实验结果

首先评价IBFs_ART的聚类质量,并从Acc,NMI和RI三个方面与G-Stream(警戒参数较多)以及模糊ART(Fuzzy ART,只有一个警戒参数)进行了比较。对于自交互,使用公式5～7,对于特征交互,使用以下三个函数：

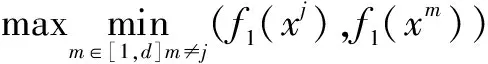
(21)

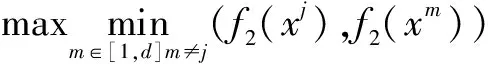
(22)

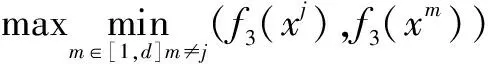
(23)

每个算法重复实验10次,聚类结果如表2～4所示。通过实验,发现取不同的ρ值,IBFs_ART算法从三个方面的评价几乎都可以找到一个a值(选取1/2和1/4值),使其性能指标均优于模糊ART,且性能指标得到不小提升,验证了IBFs_ART算法的优越性。

表2 IBFs_ART和其他数据流聚类算法Acc比较结果

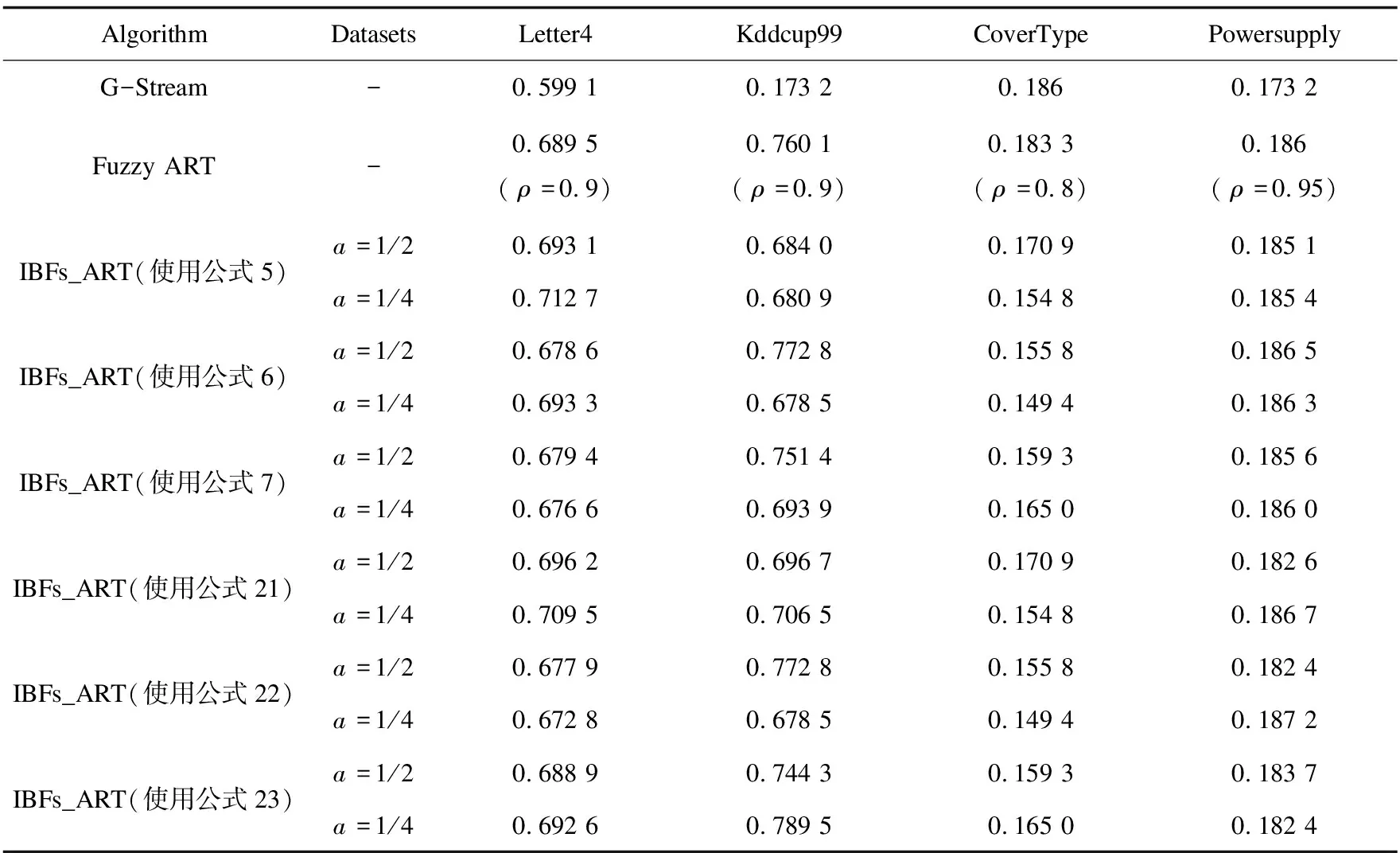
表3 IBFs_ART和其他数据流聚类算法NMI比较结果

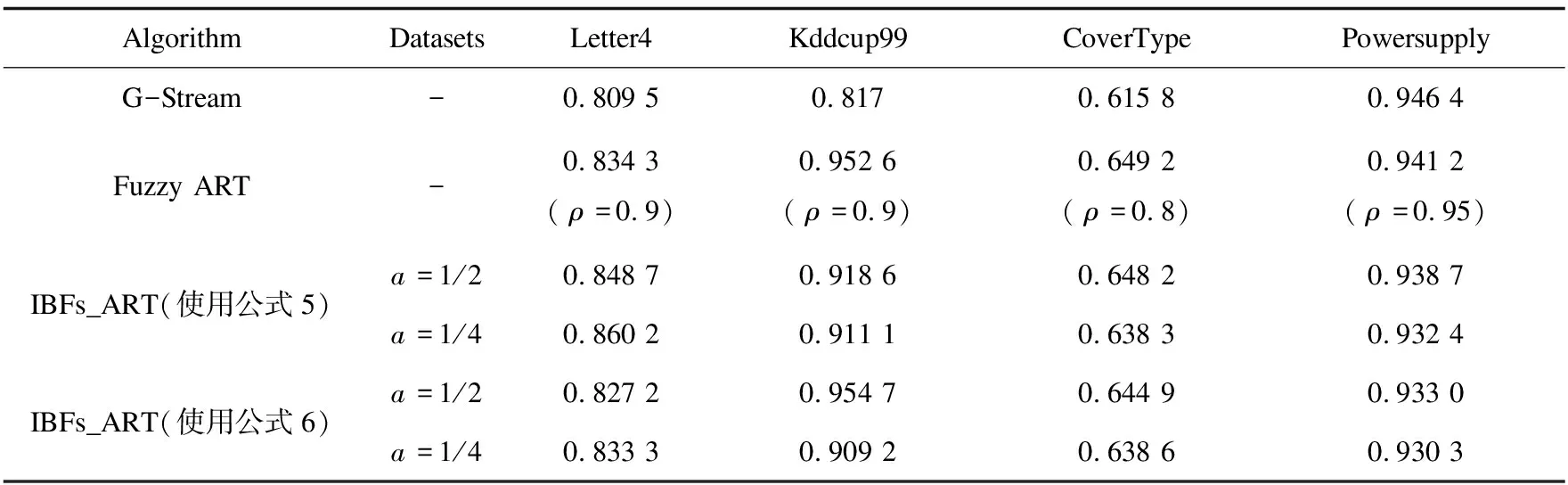
表4 IBFs_ART和其他数据流聚类算法RI比较结果

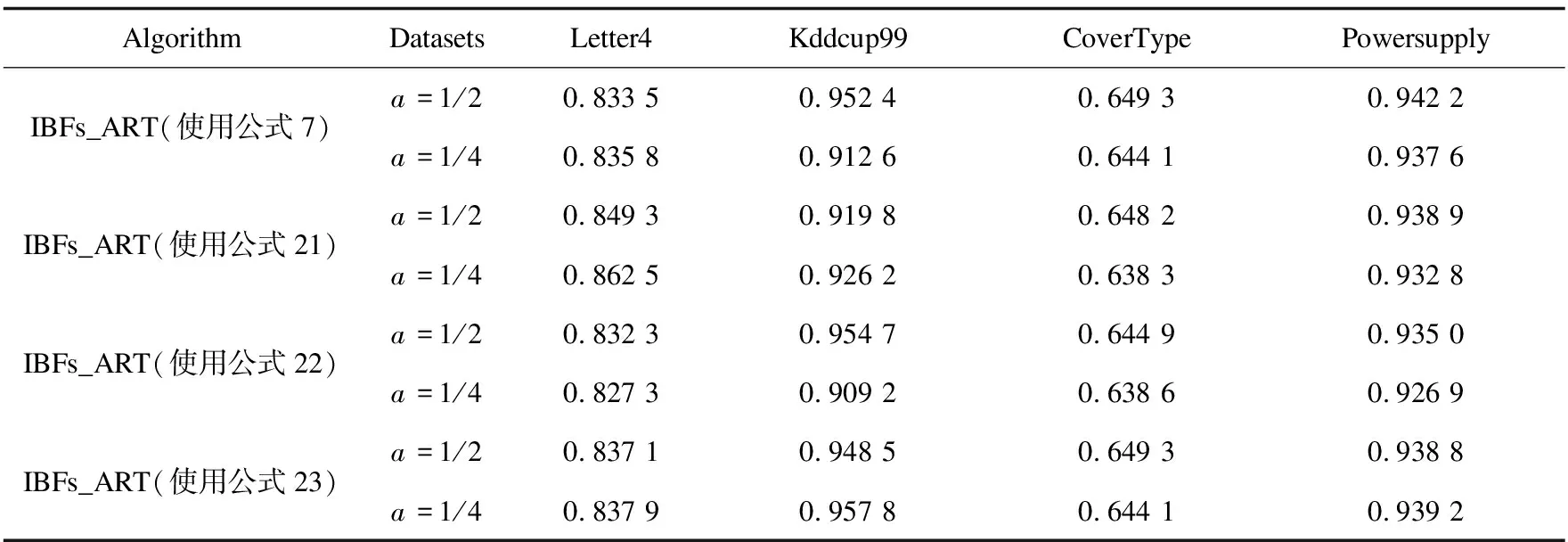
续表4

通过实验评估了不同警戒参数ρ的IBFs_ART的性能,该参数控制了当输入样本与类别发生共振时,随后是否允许该类别学习样本。实验中选择合理的警戒值ρ可以允许发现有用的簇,而不需要对许多敏感参数值进行微调。图2～5显示了IBFs_ART在4个数据集上使用Acc,NMI和RI三个评价指标展示警戒参数ρ的敏感性。

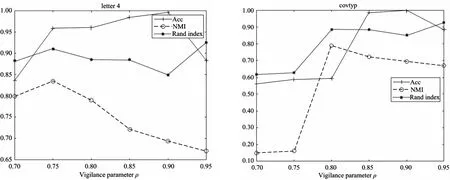
图2 IBFs_ART对于Letter4数据集ρ的敏感性 图3 IBFs_ART对于Kddcup99数据集ρ的敏感性

图4 IBFs_ART对于CoverType数据集ρ的敏感性 图5 IBFs_ART对于Powersupply数据集ρ的敏感性

通过实验,首先评价了IBFs_ART的聚类质量,并从Acc,NMI和RI三个方面将G-Stream以及模糊ART方法进行了比较,并且IBFs_ART同时采用了自交互与交叉交互。其次,采用不同的警戒参数值进行实验,证明了警戒参数对算法的影响。大量的数据结果证明,IBFs_ART可以达到更好的聚类效果与更高性能。

4 结束语

数据流是一种潜在的海量、连续、快速的数据信息序列,引起了数据挖掘领域的极大关注和研究热潮。而聚类又是数据挖掘的有效工具,因此数据流聚类无疑是数据流挖掘研究的重点。该文将交互基函数引入到模糊ART中,构造IBFs_ART算法,经过和原先算法的对比实验,验证了该算法能够提高聚类精度且只需要较低的计算成本,在Acc,NMI和RI三个方面都比传统算法模型更好,且底层模糊ART递增执行聚类的过程并没有改变,也就意味着IBFs_ART算法可以在任何算法中实现,可用于数据流聚类算法的任何扩展。