超大型组合翼伞与超大型连续翼伞的气动性能对比分析
2024-03-24段非张红英李正达陆伟伟
段非 张红英 李正达 陆伟伟
(1 南京航空航天大学航空学院飞机设计技术研究所,南京 210016)
(2 航宇救生装备有限公司,襄阳 441003)
0 引言
在空投空降领域中,随着回收物质量和尺寸的逐渐增大,需要翼伞的面积足够大,才能使回收物在有限的高度损失下获得足够小的稳定速度。当翼伞伞衣面积达到800 m2时,一般可认为是超大型翼伞。目前超大型翼伞按照组合形式可以分为超大型组合翼伞和超大型连续翼伞。顾名思义,超大型连续翼伞的伞衣是连续不断的,在制造、组装、运输等方面会面临很多困难。而模块化的翼伞,即超大型组合翼伞,可以单独更换受损模块,节省大量成本,所以超大型翼伞的模块化必定是未来的发展趋势。在性能方面,组合翼伞由于组合处的特殊性,对翼伞开伞、充气等方面都会有明显的优势,而且在组合处有气流补充,在性能上具有优越性。
目前国内外对大型翼伞已经进行了初步的研究。1998 年,美国NASA 启动了X-38 飞行器研制计划,旨在测试用于为国际空间站建造乘员返回飞行器的技术,其中就包括不同尺寸的大型翼伞[1-5]。这些翼伞在无人飞行器和载人返回飞行器计划中都承担着重要的作用,是大型冲压式翼伞最具代表性的应用。国外的研究主要从翼伞外形以及理论方法两方面展开。在外形上主要关注翼伞的前缘、后缘配置以及扰流装置对翼伞气动性能的影响[6-10]。在数值方法上,研究了非线性有限元方法、时间步长以及求解器参数选择等内容对翼伞气动性能的影响[11-19]。国内对大型翼伞的研究主要从理论推导、计算流体力学仿真、空投试验等方面进行的,研究了翼伞鼓包、下拉情况下的气动性能、翼伞侧力系数以及不同的归航算法等内容[20-24]。
目前国内外关于超大型组合翼伞气动性能的研究还非常少,因此,本文以超大型组合翼伞为研究对象,通过数值模拟的方法,研究超大型组合翼伞与连续翼伞在升阻力系数、升阻比等性能参数及不同区域气动受载上的差别。
1 数值计算方法
1.1 控制方程
翼伞的控制方程为N-S 方程,表达式为
式中u为速度矢量;ρ为密度;t为时间;ui表示速度在x轴方向的分量;p是流体微元体上的压力;μ是动力粘度;S为广义源项。
由于平均N-S 方程具有不封闭性的特点,需引入湍流模型来对方程组进行封闭处理。而标准的Kepsilon 湍流模型具有较好的稳定性和经济性以及较高的计算精度,因此它是湍流模型中应用范围最广的模型。同时,该模型还具有很好的鲁棒性,适于初始迭代、设计选型和参数研究。
1.2 超大型翼伞模型建立
本文以836 m2的翼伞为例,研究超大型组合翼伞和超大型连续翼伞的气动性能,尺寸参数如表1 所示。

表1 超大型翼伞尺寸参数表Tab.1 Dimension parameter table of oversize parafoil
836 m2超大型组合翼伞由2 个11 腔室翼伞,2 个14 腔室翼伞和1 个13 腔室翼伞组成,共有63 个气室,由58 个承载肋片连接上下翼面。同时超大型组合翼伞的连接方式为上翼面均匀选取9 个节点,下翼面选取与伞绳连接的7 个节点(除前后缘的点)进行共结点连接。定义中间气室沿展向的中心面为中轴面,整具伞沿着中轴面对称,组合处最大间距为0.288 m。
836 m2超大型连续翼伞共有63 个气室,由62 个承载肋片连接上下翼面,对称面定义及整体组合方式与超大型组合翼伞相同。
根据上述建模方法,得到两种超大型翼伞模型如图1 所示。两种翼伞下拉位置处的气室建模方法相同,其中参与下拉操作的气室翼型如图2 所示,翼型下翼面后四分之一参与变形,上翼面选取适当部分参与变形,翼型尾缘点位置满足以下两个约束:

图1 超大型翼伞无下拉模型Fig.1 Oversize parafoil without pull-down model
图2 下拉气室的翼型Fig.2 Airfoil of pull-down chamber
1)翼型尾缘点与翼伞伞绳汇合点的距离满足下拉后的操纵绳绳长;
2)翼型中上下翼面的长度与下拉前保持一致。
本文研究的冲压式翼伞近似于平滑的壁面,来流速度v=20 m/s,雷诺数Re=ρ·v·d/μ=2.19×107(其中v、d分别代表流体的流速和特征长度)。本文的气动计算可以合理假设为定常不可压湍流流动,选用K-epsilon 标准湍流模型进行求解。
1.3 计算方法准确性验证
目前计算流体力学(Computational Fluid Dynamics,CFD)方法虽然在快速发展,但结果会受网格、参数、模型算法等因素影响,造成一定的数值误差,因此需要进行试验验证。由于目前对超大型翼伞的研究还比较少,没有合适试验数据可以作为仿真计算的参考,因此本文参考相同翼型的其他翼伞,对本文的数值模拟方法进行算例验证。Desabrais 选择美军常用的MC-4 翼伞作为研究对象,分别进行了风洞试验和空投试验。该试验选用的翼伞模型为半刚性模型,即建立坚固的翼型肋片并选用柔性织物作为伞衣的材料,通过在伞衣上布置的细线观察翼伞周围空气的流动情况[25]。试验是在麻省理工学院莱特兄弟风洞进行的,这是一个封闭的回流式风洞。风洞中的气流速度设置为12.0 m/s,得出雷诺数Re=8.2×105。实物图如图3 和图4 所示。该实验思路严谨、方法科学结果合理。因此参考Desabrais 所做的风洞试验,验证本文模型的合理性和适用性,并验证网格的无关性,验证仿真计算方法的准确性。

图3 风洞试验翼伞模型内部刚性结构Fig.3 Internal rigid structure of the wind tunnel test parafoil model

图4 风洞试验测试过程中的翼伞模型照片Fig.4 Photos of the parafoil model during the wind tunnel test process
1.3.1 湍流适用性验证
本文参考上述文献中的模型数据,建立三维翼伞仿真模型。选用相同翼型作为肋片截面,设置14 个半气室,每个半气室宽为0.143 m。翼伞展长为2 m,弦长为1 m,展弦比为2∶1,面积为2 m2,三维仿真模型如图5 所示。
图5 三维翼伞仿真模型Fig.5 3D parachute simulation model
选择翼伞飞行时较为稳定的2°攻角和8°攻角作为参考,进行CFD 仿真计算,设置每2°一个攻角,共四种工况。选择雷诺平均N-S 方程作为控制方程,采用有限体积法作为离散化方法。本文选择目前计算流体力学常用的一方程模型S-A 模型、两方程k-ω SST 模型与k-ε 标准模型进行湍流无关性验证。
由于试验过程中翼伞受气动干扰、空气摩擦等方面的影响,整体受到的阻力不稳定性较大。因此本文选定对翼伞气动性能起决定性影响的升力系数作为对比参数,进行固定来流速度、不同攻角时的仿真计算,并将得到的仿真计算结果与文献中的风洞试验结果相对比,结果如图6 所示。考虑到计算成本及主要分析对象,计算过程中假定翼伞模型为刚性且伞衣透气性为0。
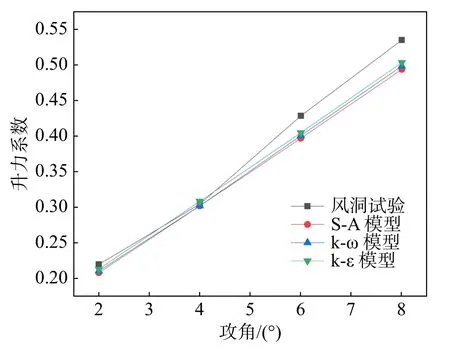
图6 风洞试验与仿真模拟结果对比Fig.6 Comparison of wind tunnel test and simulation
翼伞升力系数的仿真结果与风洞试验结果非常接近,在攻角α= 4°时误差最小,在α=8°时误差略大。不同湍流模型仿真的结果非常接近。k-ε 标准模型计算结果与风洞试验结果更为接近,误差最小时仅为1.22%,最大时为5.89%,较之一方程模型S-A 模型与两方程k-ωSST 模型误差更小,可以验证本文选择k-ε 标准模型的合理性。
导致仿真结果与风洞试验结果产生误差的原因有很多,比如试验采用的柔性伞衣的非线性动力学结构与仿真刚性结构的差异;试验中伞衣张开后的鼓包结构与仿真中未鼓包结构的差异;实验过程中的试验件加工误差、测量误差、环境因素等问题;以及仿真计算过程中的模型误差、舍入误差、截断误差等等。因此,此误差在可以接受的范围,足以证明本文的数值模拟方法在翼伞气动性能问题上有较高的准确性。
1.3.2 网格无关性验证
为了确保计算过程中网格数量不会对计算结果造成影响,在前节的基础上进行网格无关性验证。建立多个不同的网格模型,网格量范围为3.3×105~2.2×106。以α=4°时的计算工况为例,将计算得到的升力系数与风洞试验结果进行对比,误差如表2 所示。

表2 网格无关性验证Tab.2 Grid independence verification
从表中可以看出,不同网格量得到的仿真结果与风洞试验误差很小,误差范围为0.89%~2.63%,可以说明计算结果与网格数量无关。综合计算精度、计算耗费等问题,选择1.78×105网格量的设置作为本文网格模型建立的方法。
2 组合翼伞与连续翼伞无下拉状态气动性能对比
将超大型连续翼伞和超大型组合翼伞无下拉情况的气动特性仿真结果进行对比,分析它们的异同。本文对仿真模拟做出以下假设:1)翼伞计算模型均做刚性化处理;2)认为伞衣材料透气性为零;3)忽略伞绳对气动力的影响,伞绳不参与气动计算;4)在流动情况确定的条件下,做定常流动处理。
2.1 气动特性对比
升阻力系数参考面积为836 m2,动压为245 Pa,参考长度为16 m,俯仰力矩取距点为翼伞对称面内翼型的前四分之一弦线处,以前缘向下转动为正向。将连续伞与组合伞的升阻力系数、升阻比和俯仰力矩系数对比,如图7 所示。攻角α的取值为-8°~28°,每4°为一个工况。
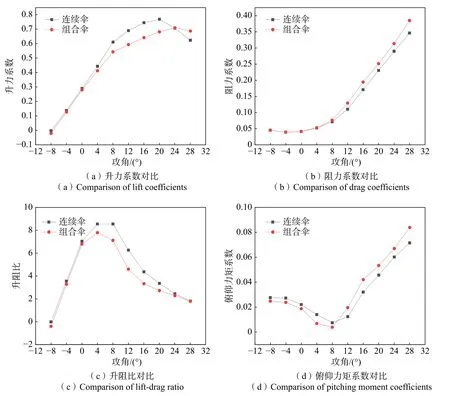
图7 连续伞与组合伞无下拉状态气动参数对比Fig.7 Comparison of aerodynamic performance between two parafoil without pull-down
图8 为连续伞与组合伞无下拉状态二维流场对比,从图中可以看出,上翼面前缘为高压区,气流绕过上翼面最高点,压强显著下降,形成低压区。随着攻角增大,上翼面低压区的位置前移,切口处的压强增大。小攻角时,上翼面流动非常平缓,气流附体效果非常好,没有流动分离,因此连续伞和组合伞的升、阻力系数相差无几(见图7(a)、(b))。在α=4°时两具伞升阻比达到最大(见图7(c)),下翼面前缘切口附近产生了分离气泡,这是翼伞特有的绕流流态。事实上,由于切口处气流受滞止压力外翻形成较大的切口处法向速度,在整个考察攻角范围内前缘切口下缘均会有规模不等的分离气泡,随着迎角增大逐渐减弱(见图8)。从α=4°开始,连续伞升力系数开始比组合伞的升力系数大一些,这是因为组合伞后缘的附体效果较差,开始出现边界层分离的情况,而连续伞的附体效果较好,所以升力系数略大。两具伞沿前缘切口压力梯度均较大,且气室内压力很高变化很小,这是保持翼伞剖面翼型的动力。
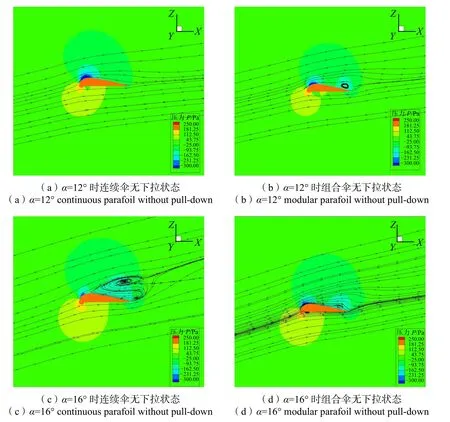
图8 连续伞与组合伞无下拉状态二维流场对比Fig.8 Comparison of two-dimensional flow field of two parafoil without pull-down
随着攻角的增大,上翼面逐渐出现流动分离的情况。组合翼伞气流附体效果较好,在α=12°时(见图8(a)、(b)),由于组合处有气流补充,与上翼面附体气流相遇,后缘处会产生一个小的附着涡,之后逐渐消失。对于连续伞,气流分离的情况首次在α=16°时出现(见图8(c)、(d)),会在翼伞上部出现一个附着涡,在后缘处形成一个自由涡。而在攻角增大的过程中,上翼面前缘处的附着涡和后缘处的自由涡也随之增大,尤其是附着涡增大更加明显。组合翼伞的附着涡并不会随着攻角的增大而有明显的变化,只有后缘处的自由涡会因为攻角的增大逐渐增大。与连续翼伞相比,组合翼伞自由涡要明显小很多,附着涡则相对较大。这是因为组合翼伞会有部分气流通过组合处从下翼面补充到上翼面低压区,而连续翼伞气流只能从下翼面流出。攻角增大过程中,组合伞上翼面组合处低压区变小,尾部有气流从下翼面流至上翼面,导致升力下降。攻角继续增大,组合伞上翼面整体低压区变小,组合处的区别对整体升力的影响也随之变小,组合伞与连续伞升力系数趋于相近。连续翼伞的流动分离现象比组合翼伞要明显很多,这正是组合处可以有气流补充带来的影响。
连续伞与组合伞的阻力系数整体差距较小,特别是负攻角和小攻角情况下,最小阻力系数均在α=0°左右。连续伞和组合伞升阻比趋势基本相同,均为先增后降,最大升阻比在α=8°附近。由于升力系数和阻力系数在α=8°时两伞出现差异,所以升阻比也在此攻角下有较大差异。组合伞与连续伞的俯仰力矩系数趋势相同(见图7(d))。在α=8°之前,连续伞的俯仰力矩系数较大,之后,则组合伞较大。由翼伞静稳定条件可知,当俯仰力矩系数斜率为负时翼伞稳定,所以在α=8°之前,翼伞基本稳定。
2.2 三维流场对比
从三维流场图来看,小攻角时翼伞上下翼面前缘均有负压区,说明此处流速比较大。随着攻角的增大,上翼面负压区逐渐减小,位置前移,下翼面负压区消失,压力分布相对均匀。组合伞负压区面积比连续伞要略小,导致组合伞升力小于连续伞。翼伞中间气室内的压力比边缘气室更大,因此边缘气室前方压力会小一些,进而导致边缘气室内部压力较小。小攻角下,两伞的流动附体效果明显,基本没有流动分离情况。随着攻角增大,翼伞中间气室的上表面有明显的流动分离情况,攻角越大,流动分离越严重。边缘气室尾部尖端会有涡流产生,下表面压强大于上表面,产生下洗流过程中会产生此涡流,攻角越大,涡流强度越大。由于下洗作用的存在,边缘气室提供的升力会小于中间气室。连续伞在α=16°时产生流动分离(见图9),而组合伞由于组合处有气流补充至上翼面,虽然降低了升力,但同时也延缓了流动分离,所以在α=24°时才失速,升力最大值出现在α=24°。

图9 连续伞与组合伞无下拉状态16°攻角三维流线图Fig.9 Three dimensional streamline diagram of two parafoil without pull-down at 16 ° angle of attack
3 组合翼伞与连续翼伞下拉状态气动性能对比
本章对超大型连续翼伞与超大型组合翼伞单侧下拉与双侧下拉状态下的气动特性仿真结果进行对比分析。
3.1 单侧下拉气动特性对比
单侧下拉参数设置与无下拉状态相同。单侧下拉时超大型连续翼伞与超大型组合翼伞气动计算结果如图10 所示。
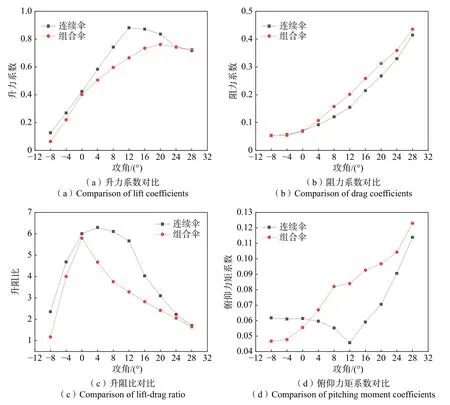
图10 连续伞与组合伞单侧下拉状态气动参数对比Fig.10 Comparison of aerodynamic parameters between two parafoil in single side pull-down
从升力系数对比图可以看到,对于负攻角,连续伞和组合伞的升力系数差别不大。从流场上看,组合伞的低压区面积要比连续伞略小,这也是组合伞升力系数更小的原因。随着攻角的增大,连续伞上翼面上部出现附着涡,后缘处出现自由涡,两处的涡大小相同,且涡的大小并不随着攻角的增大而增大。连续伞的升力系数增大趋势更加明显,从流场上看,在α=12°时(见图11(a)、(b))上下翼面压差最大,升力达到最大值,随后逐渐减小(见图11(c)、(d))。而组合伞增幅始终比较平滑,在α=20°时(见图11(e)、(f)),仅出现了后缘处的自由涡,这是因为组合伞在组合处有气流补充,降低了上翼面低压区的压强,达到最大升力系数。两具伞的阻力系数都保持随攻角的增大而逐渐增大,差别并不明显。
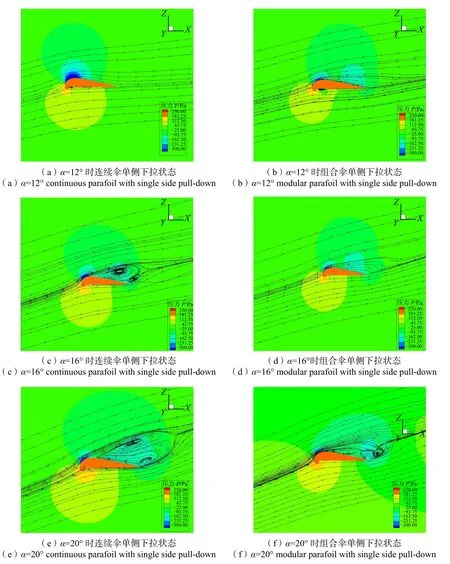
图11 连续伞与组合伞单侧下拉状态二维流场对比Fig.11 Comparison of two-dimensional flow field of two parafoil in single side pull-down
由于升力系数的差异,所以升阻比也产生了明显不同。升力在小攻角下增幅较为明显,之后增幅放缓;而阻力系数增幅较为平均,因此升阻比出现了先增大后减小的趋势。不同的是,连续伞的最大升阻比出现在α=8°附近,而组合伞的最大升阻比出现在了α=4°附近。两具伞的俯仰力矩系数差别明显。连续伞先减小后增大,在α=12°时最小。而组合伞俯仰力矩系数保持增大的趋势,虽然在α=0°之前,组合伞俯仰力矩系数较小;但在α=4°之后,组合伞始终比连续伞要大。在流场图中可以明显看到,α=12°时,连续伞的低压区只分布在翼伞前缘。而组合伞的低压区除了翼伞前缘,在翼伞后缘附近也有分布,使得翼伞在弦向增加了一个力矩,因此组合伞在α=12°时俯仰力矩系数取到最小值,这与无下拉时翼伞的俯仰力矩系数变化趋势相似,说明组合伞受下拉的影响更小,在α=12°之前组合伞基本保持静稳定。
从图12 的三维流线图可以看出,在小攻角时,连续伞上翼面低压区主要在翼伞前缘附近沿展向均匀分布,其余低压区集中在下拉一侧的翼尖处。随着攻角的增大,前缘低压区呈现中间减少两边增加的趋势,攻角越大,前缘中间的低压区越小。同时,最外侧气室上表面的低压区逐渐增大,导致边缘气室的上下表面压差增加。所以气流更多地从翼伞两侧向上绕流,两侧翼尖出现涡流,攻角越大,涡流越明显。受到下拉的影响,下拉一侧涡流明显。这是由于下拉改变了翼型从而改变了翼伞两侧的升力,翼伞得以转弯。
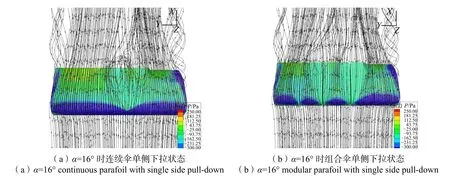
图12 连续伞与组合伞单侧下拉状态16°攻角三维流线图Fig.12 Three dimensional streamline diagram of two parafoil in single side pull-down at 16 ° angle of attack
3.2 双侧下拉气动特性对比
双侧下拉参数设置与无下拉状态相同,结果如图13 所示。组合伞与连续伞在双侧下拉时升力系数差别不大。升力系数先增大后减小,在α=12°时出现最大升力系数。在α=16°时(见图14(a)、(b)),连续伞出现了流动分离的情况,上翼面分别出现了一个自由涡和一个附着涡。而组合伞在α=16°时,并没有出现涡,气流附体效果很好。到α=24°时(见图14(c)、(d)),两具伞上翼面的涡流都发生了明显变化。连续伞前缘处的附着涡显著增大,并且位置上移,后缘处的自由涡逐渐减小,低压区集中在翼伞上表面。而组合伞逐渐开始出现流动分离情况,后缘处的自由涡逐渐增大,低压区则主要出现在翼伞后缘处附近。两具伞的阻力系数都随着攻角的增大而均匀增大。由于组合伞升力略小,阻力略大,导致升阻比明显小于连续伞。但两具伞升阻比变化趋势相同,最大升阻比在0°~4°之间。在大攻角下,二者差距逐渐减小。而两具伞的俯仰力矩系数变化趋势也几乎相同,均随攻角逐渐增大。

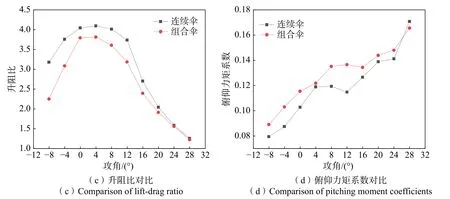
图13 连续伞与组合伞双侧下拉状态气动参数对比Fig.13 Comparison of aerodynamic parameters between two parafoil with double side pull-down state
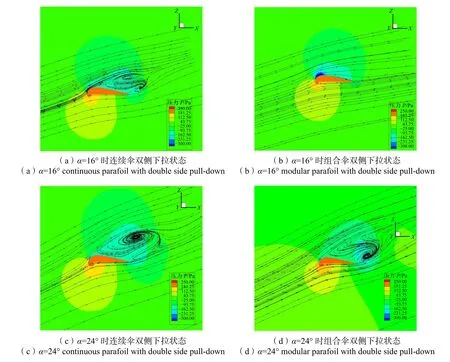
图14 连续伞与组合伞双侧下拉状态二维流场对比Fig.14 Comparison of two-dimensional flow field of two parafoil with double side pull-down
4 结论
本文对超大型连续翼伞和超大型组合翼伞进行仿真计算,将气动性能进行对比,得到如下结论:
1)相比连续翼伞,组合翼伞虽然最大升力较小,但是有更大的失速攻角,极大地减缓了翼伞的流动分离情况,组合伞的升阻比也因此有所减小。
2)在α=16°时,连续伞已经出现流动分离的情况,在上翼面出现了两个涡。而组合伞由于气流补充,气流的附体效果很好,在α=16°并未出现分离的情况,没有涡的产生。因此组合翼伞更适合大攻角的飞行状态。
3)气流在通过组合处后会先向低压区补充,所以组合伞在组合处附近的压力略大,低压区主要分布在各个模块的中部。
4)组合伞受单侧下拉的影响更小,有更好的稳定性,在α=12°之前组合伞基本保持静稳定。
