城市轨道交通线路建设时序研究

葛馨茹

摘 要：为合理决策轨道交通建设时序，将城市轨道交通线路建设时序的确定视为多因素决策问题，提出基于Pythagorean模糊熵的优劣解距离法。将传统的一次性静态建设时序确定过程转化为多次动态决策，综合考虑决策者在不同时段对决定线路建设时序的各影响因素重视程度不同，为影响因素指标赋权，计算各时段未确定建设时序的線路与理想解的综合贴近度，进而确定线路建设时序。应用所提出的决策方法确定重庆市城市轨道交通第四期规划线路建设时序，与实际规划时序基本一致。

关键词：城市轨道交通 线路动态建设时序 Pythagorean模糊熵 TOPSIS模型

城市轨道交通建设具有周期性长、成本较高、建成后调整难度大等特性，合理且具有前瞻性的线网规划至关重要。目前，国内外学者对于城市轨道交通项目建设时序确定的研究相对较少。概括来讲，已有的研究思路主要归为两类，一类是引入某种思想或是基于某种决策方法，量化各线路的重要程度，进而对其建设优先级加以排序；另一类是从线网整体角度分析，构建成本—效益模型，计算不同建设顺序所对应的成本与效益，选择综合效益最大的建设方案。文献[1]引入格序决策理论，依据灰色关联分析法，比较各条线路与理想方案的综合偏差大小，确定建设时序。文献[2]对线路各站点建立节点重要性指标，量化加权累加得到各线路重要度，依据评价结果确定建设时序。文献[3]基于累计前景理论，构建成本-效益最大化优化模型，计算不同建设时序的线网建设方案的综合前景值，确定最优建设时序方案。尽管现有研究成果可以一定程度上帮助轨道交通建设时序决策者有效度量线网中各线路的相对重要性，但多关注静态层面，确定建设时序时没有考虑线路逐渐网络化的动态过程，忽视优先建设线路对其余规划线路的影响。

因此，本文将传统的一次性静态建设时序确定过程动态化，将其转化为多次动态决策，且考虑不同建设时段决策者对各影响因素重视程度的差异，对规划线路的建设时序进行综合确定，使决策结果更贴近工程实际。

1 建设时序影响因素指标体系构建

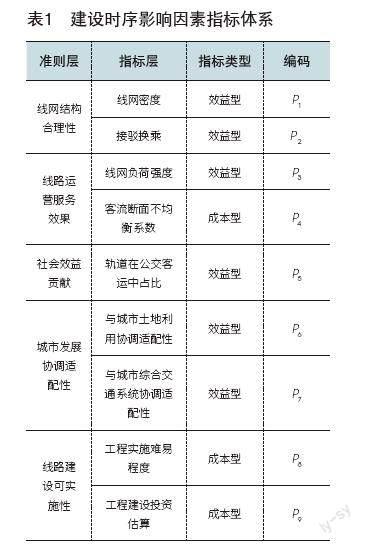
合理的构建线路建设时序影响因素指标体系是科学确定建设方案的前提，对影响因素的选取既要全面分析，又不应繁复冗杂。本文重点梳理提炼文献[4-6]中的共性指标，并结合上海、北京、西安、柳州等城市轨道交通线网规划综合评价中所采用的指标体系，从线路的结构性、线路运营后对居民出行需求的满足性、线路建设的可实施性、线路建设对社会效益的贡献情况以及线路建设与城市发展的协调适配性等角度，构建线路建设时序影响因素指标体系，具体各级评价指标如表1所示。

2 线路建设时序动态决策模型构建

城市轨道交通线路建设时序的确定可以归结为多属性决策问题。考虑到在线路成“网”过程的不同阶段中，决策者对于线路建设时序各影响因素指标的重视程度并非一成不变，而是动态变化的，采用Pythagorean模糊熵构建非线性规划模型[15，16]，确定随着建设优先级较高线路的建成，不同阶段线路建设时序各影响因素指标的权重，得到各阶段相应的决策矩阵，应用理想解法计算各线路在不同建设阶段的正负理想解距离，依据与理想方案贴进度大小确定线路建设时序。

2.1 线路建设时序决策问题描述

假设城市轨交线网规划近期建设n条线路，线路集为，建设时段为，不同建设时段权重集，线网建设时序影响因素集为，影响因素权重集。用Zij表示线路li中第j项影响因素相对应的评价值，其中，。那么线路集L的原始各影响因素评价矩阵为。

通常各影响因素的评价值量纲不同，对其加以无量纲标准化处理。

2.2 确定指标权重

线路建设时序各影响因素权重的设定，除了要兼顾各影响因素指标间的客观内在联系与专家的自身经历和主观经验，还需考虑到建设优先级较高的线路实施运营后，对未建设的既有规划线路后续建设时序的影响。本文引入Pythagorean模糊数的概念，用表示线路在建设时序影响因素下的指标评价值，其中tm时段线路li对影响因素pj的满意度用表示，线路li对影响因素pj的不满意度用表示。

2.2.1 确定建设时段权重

本文对线路不同建设时段赋权重点考虑城市发展现状及近期规划，淡化对远期城市发展规划的考量，参照文献[7]，应用泊松分布法逆形式确定权重。

则有不同建设时段权重集，其中表示tm时段的时间权重，约束条件为：。

2.2.2 确定不同时段建设时序影响因素

对于城市轨道交通线路建设时序的确定，各影响因素评价指标的重要程度不同，在线路网络化过程的不同时段，决策者对线路建设时序决策属性的重点也会有所改变，因此对不同时段不同影响因素指标赋予的权重也有一定的差别。本文对不同时段建设时序各影响因素权重的具体计算过程如下：

建立建设过程中tm时段的Pythagorean模糊决策矩阵。

计算建设过程中tm时段线路建设时序影响因素的Pythagorean模糊熵。

其中，表示对线路j属性决策犹豫度，

构建各时段线路建设时序影响因素权重的最优化模型。

式中，表示tm时段线路建设时序影响因素pj对应的属性权重，约束条件为：。

2.3 建设时序决策矩阵

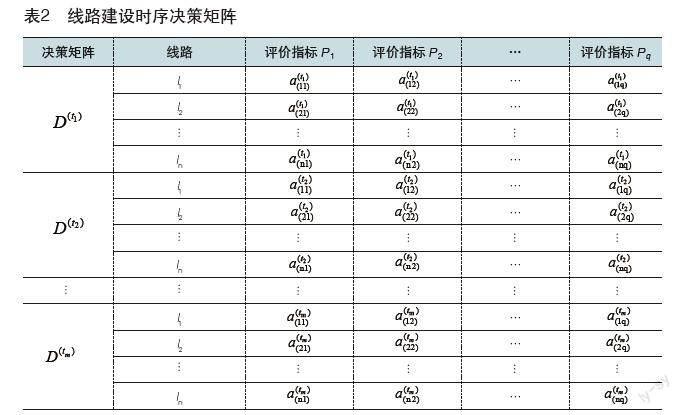
依照城市轨道交通线路建设各时段的Pythagorean模糊决策矩阵，整理可得到n条规划线路q个影响线路建设时序指标的m个时段的Pythagorean模糊决策矩阵，如表2所示。

2.4 线路建设时序排序决策步骤

（1）将线路建设中各时段的Pythagorean模糊矩阵整理为Pythagorean综合模糊矩阵。

（2）依照式（3）计算建设时段权重。

（3）分别计算各时段Pythagorean模糊加权决策矩阵的正理想解方案与负理想解方案，其中。

（4）分别计算规划中尚未确定建设时序的各条线路li在某一相同时段评价值到正理想解方案M+与负理想解方案M-的距离，本文采用欧氏距离（Euclidean distance）来度量。

（5）分别计算规划中尚未确定建设时序的各条线路li在同一时段评价值与理想解的综合贴进度Ci，按照Ci数值大小排序来确定各条线路的建设时序。

3 实例分析

2020年，《重庆市城市轨道交通第四期建设规划（2020～2025年）》获国家发展和改革委员会批复。本文选取其中规划第一批需要建设的9条线路（4号线西延伸段、6号线重庆东站延伸段、7号线一期、8号线一期、15号线、17号线一期、18号线渝中区延伸段、24号线一期、27号线），参照重庆市统计局公示的资料及各线路工程可行性客流预测与分析报告获取交通影响指标数据，应用本文所构建的动态决策模型确定线路建设顺序。

对9条线路进行编号，如表3所示。

对线路建设时序影响因素指标进行无量纲标准化计算，按照式（4）、（5）、（6），得到各时段影响因素的权重，本文将这9条规划线路建设时序划分为4个阶段，计算t1～t4各时段的Pythagorean综合模糊矩阵，结果如表4所示。

依据式（3），令，计算得到不同建设时段权重，如表5所示。

依据各时段Pythagorean模糊加权决策矩阵和Pythagorean模糊数的基本运算，计算时序加权矩阵，依据式（7）、（8）、（9），首先计算t1时段，规划中各条线路l1到正理想解方案M+与负理想解方案M-的距离，计算与理想解的综合贴近度Ci，如表6所示。

由t1时段各线路综合贴进度大小可知线路l1最为贴近理想解，确定最先建设线路l1。接下来计算t2时段尚未确定建设时序的各条线路li到正理想解方案M+与负理想解方案M-的距离，计算与理想解的综合贴进度Ci，直至t4时段。

将计算得到的各条线路li在某一相同时段评价值与理想解的综合贴度Ci，按照综合贴进度Ci数值大小排序来确定各条线路的建设时序为：l1>l2l3l5l7> l4> l6l8l9。

《重庆市城市轨道交通第四期建设规划（2020～2025年）》中实际规划情况为：规划4号线西延伸段、6号线重庆东站延伸段于2023年建成，7号线一期、15号线、18号线渝中区延伸段于2024年建成，8号线一期于2025年建成，17号线一期、24号线一期和27号线于2026年建成。

4 结语

（1）本文将城市轨道交通线路建设时序的确定转化为多因素动态决策问题，提出基于Pythagorean模糊熵的优劣解距离法，计算各时段各线路与理想解的综合贴近度，排序确定线路建设时序。

（2）对线路建设时序影响因素指标赋权，兼顾各影响因素指标间的客观内在联系及专家的主观经验，并考虑到线路网络化过程的不同建设时段，决策者对各影响因素重视程度不同，引入Pythagorean模糊数的概念，为不同时段影响因素指标赋权。

（3）考虑到线路网络化过程中，建设优先级较高的线路实施运营后，对未建设的既有规划线路后续建设时序的影响，将传统的一次性静态建设时序确定过程转化为多次动态决策，逐步计算未确定建设时序的规划线路与理想解的综合贴进度，选择相对较为迫切的建设线路。

（4）应用所提出的线路建设时序决策方法，确定重庆市城市轨道交通第四期规划线路建设时序，与实际规划时序基本一致，验证本文所提出的决策方法具有实际应用价值。

（5）本文所提出的城市轨道交通线路动态建设时序确定方法只能判断各线路的建设先后顺序，无法确定规划线路的建设时机，还有待后续深化研究。

参考文献：

[1]张桐，金键，沈犁，等.基于灰色格序决策理论的城市轨道交通建设项目时序确定方法[J].城市轨道交通研究，2016，19（10）：102-105+133.

[2]张鹍鹏.节点重要度理论下的轨道交通线路建设时序模型分析[J].现代电子技术，2021，44（23）：126-129.

[3]郭延永，刘攀，吴瑶.基于累计前景理论的城市轨道交通建设时序[J].交通运输系统工程与信息，2013，13（04）：29-35.

[4]孙然然，陈家旭，李晓璐，张彭，朱广宇.面向运营安全的城市轨道交通线网性能综合评价[J].科学技术与工程，2020，20（36）：15067-15073.

[5]呂颖.都市圈综合轨道交通线网布局评价指标研究[J].铁道标准设计，2021，65（04）：25-30+35.

[6]石红国，贺玉姣.基于D-S证据理论的城市轨道交通线网规划评价研究[J].铁道运输与经济，2018，40（02）：87-93.

[7]陈德江，王君，张浩为.基于直觉模糊多属性决策的动态威胁评估模型[J].计算机科学，2019，46（04）：183-188.