CAUCHY TYPE INTEGRALS AND A BOUNDARY VALUE PROBLEM IN A COMPLEX CLIFFORD ANALYSIS*

(曹南斌)

School of Mathematics and Science, Hebei GEO University, Shijiazhuang 050031, China E-mail: caonanbin@163.com

Zunfeng LI (李尊凤)† Heju YANG (杨贺菊)

College of Science, Hebei University of Science and Technology, Shijiazhuang 050018, China E-mail: zunfeng928@163.com; earnestqin@163.com

Yuying QIAO (乔玉英)

School of Mathematical Sciences, Hebei Normal University, Shijiazhuang 050024, China E-mail: yuyingqiao@163.com

Abstract Clifford analysis is an important branch of modern analysis; it has a very important theoretical significance and application value, and its conclusions can be applied to the Maxwell equation, Yang-Mill field theory, quantum mechanics and value problems.In this paper, we first give the definition of a quasi-Cauchy type integral in complex Clifford analysis, and get the Plemelj formula for it.Second, we discuss the H¨older continuity for the Cauchy-type integral operators with values in a complex Clifford algebra.Finally, we prove the existence of solutions for a class of linear boundary value problems and give the integral representation for the solution.

Key words Clifford analysis; Cauchy type integral; Plemelj formula; H¨older continuous;boundary value problems

1 Introduction

Boundary value problems are always a hot topic in mathematics and physics.Singular integral operators are useful for solving boundary value problems for partial differential equations;they are the core components of the solutions of boundary value problems.Since the 1960’s,Vekuaet al.began to study the singular integral operators on the complex plane, and established a set of basic theories for singular integral operators [1,2].Because of the importance of these theories, they have attracted the attention of many scholars.Both mathematical theory and practical problems need the classical complex analysis in order to develop into higher dimensional space [3].

Clifford analysis is one of the important generalizations of classical complex analysis in higher space, and it has important theoretical significance and application value [4-8].There are many significant applications in neural networks [5,6], and signal processing [7].Vekua and coauthors studied the dynamics of anti-periodic solutions on Clifford-valued high-order Hopfield neural networks with multi-proportional delays.In 2018, Liuet al.developed a Clifford algebra valued boundary element method to solve the three-dimensional problems of elasticity numerically, and obtained a system of algebraic equations.Moreover, numerical results of interior and exterior problems with smooth and nonsmooth boundaries were derived using the linear interpolation isoparametric and triangular elements,and the Gauss quadrature verified the accuracy of the singularity-free boundary element method [8].

Developments in the study of Clifford singular integral operators have made it possible to apply Clifford analysis techniques as a tool for studying a variety of boundary problems.In particular, some properties of the Cauchy type integral and the Plemelj formula play an important role in solving boundary value problems.Duet al.discussed the boundary behavior for the Cauchy-type integrals with values in a Clifford algebra,and obtained a Sochocki-Plemelj formula and Privalov-Muskhelishvili theorems for the Cauchy-type integral taken over a smooth surface by a rather simple method [9].

Lianetet al.proved that the higher order Lipschitz classes behave invariantly under the action of a singular integral operator naturally arising in a polyanalytic function theory.Then they provided a generalization of the well-known theorem by Joseph Plemelj and Ivan Privalov[10].

In recent years, a great deal of work about the integral expressions and properties of the regular functions, the Plemelj formula and boundary value problems in real Clifford analysis have been presented [11-21].

In 2018, Liet al.constructed an analogue of the Bochner-Martinelli kernel based on the theory of functions of several complex analysis and obtained the Cauchy integral formula in a complex Clifford analysis; this gave the integral representation of the regular function in the complex Clifford analysis [22].In the same year, Liet al.studied the properties of T operators with a B-M Kernel in complex Clifford analysis[23].These conclusions enriched the theoretical knowledge of the complex Clifford analysis and laid the solid and powerful foundation which this paper is built.In this paper, we will study quasi-Cauchy integrals and their applications to boundary value problems in complex Clifford analysis.

The rest of this paper is organized as follows: in Section 2, we briefly introduce Clifford algebra, the definition of complex regular functions, and the conclusions to be used in this article.In Section 3, we give the definition of a quasi-Cauchy type integral in complex Clifford analysis.We get the Plemelj formula of the quasi-Cauchy type integral with a B-M kernel in complex Clifford analysis.In Section 4, we discuss the H¨older continuity the Cauchy-type integral operators with values in complex Clifford algebra.In Section 5, we prove the existence of solutions for a class of linear boundary value problems and give the integral representation for the solution.

2 Preliminaries

We introduce the Dirac operator

Remarks:Dlf(z)=0 is also written asDf(z)=0;Drf(z)=0 is also written asf(z)D=0.

Lemma 2.3([22] Stokes formula in the complex Clifford analysis) Suppose that Ω⊂Cn+1is a bounded domain,and thatf,g ∈C1(Ω,Cl0,n).Then,for eachn+1 chain Γ⊂Cn+1,

where dvz= dx0∧dx1∧···∧dxn ∧dy0∧dy1∧···∧dyn,xj ∈R,yj ∈R,j= 0,1,···,n,zj=xj+iyj, dσz=dσ1z+dσ2z.

Lemma 2.4([22] Cauchy Integral Formula) Suppose that Ω and Γ are as above, and letfbe complex right regular in Ω.Then for each Γ⊂Ω, and for anyz ∈Γ,

Lemma 2.5([22]) For anyξ/=z,

Let Ω⊂R2n+2(～=Cn+1) be a nonempty bounded domain, whose boundary∂Ω is an oriented differentiable and compact Liapunov surface (see [24]).LetN0∈∂Ω be a fixed point.We take a coordinate system with the origin atN0and let the outward normal direction of∂Ω atN0have the direction of the positiveξ2n+1axis.Then the surface∂Ω can be written asξ2n+1=ξ2n+1(ξ0,ξ1,···,ξ2n), andξ2n+1has partial derivatives onξi(i=0,1,···,2n).We take a polar coordinate atN0with

Φf(z) is a normal integral whenz ∈Cn+1∂Ω; Φf(z) is a singular integral whenz ∈∂Ω.

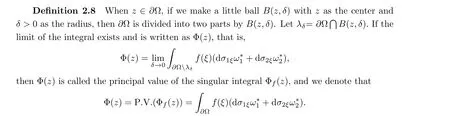
In the next sections we use the convention thatM, with certain subscripts, denotes a constant,depending on some functions,sets or parameters,and that its value may change from time to time.

3 Plemelj Formula

This conclusion can be proven by Lemmas 2.3 and 2.5.

From Theorem 3.1 and Lemma 2.4 we can easily get the following conclusions.

Corollary 3.2 Suppose that Ω,Uare as described in Theorem 3.1, and that∂Ω is a smooth, compact, and orientable Liapunov surface.Then

The theorem is proven.□

The following results can be obtained from the proof process of Theorem 3.3:

Corollary 3.4Suppose that Ω,Uand∂Ω are as described in Corollary 3.2.Whenz ∈∂Ω, we have that

Make a open ballB(z0,δ) withzas the center andδ ＞0 as the radius.Then∂Ω is divided into two parts byB(z0,δ).The part located on the surface∂Ω and inside the ballB(z0,δ) is denoted asλδ, so

Thus, for arbitraryε ＞0, there is a constantρ ＞0, when 0＜δ ＜ρ, such thatI12＜Mε.Take a fixed constantδsuch that 0＜δ ＜ρ, and whenξ ∈∂Ωλδ, by Lemma 2.6,

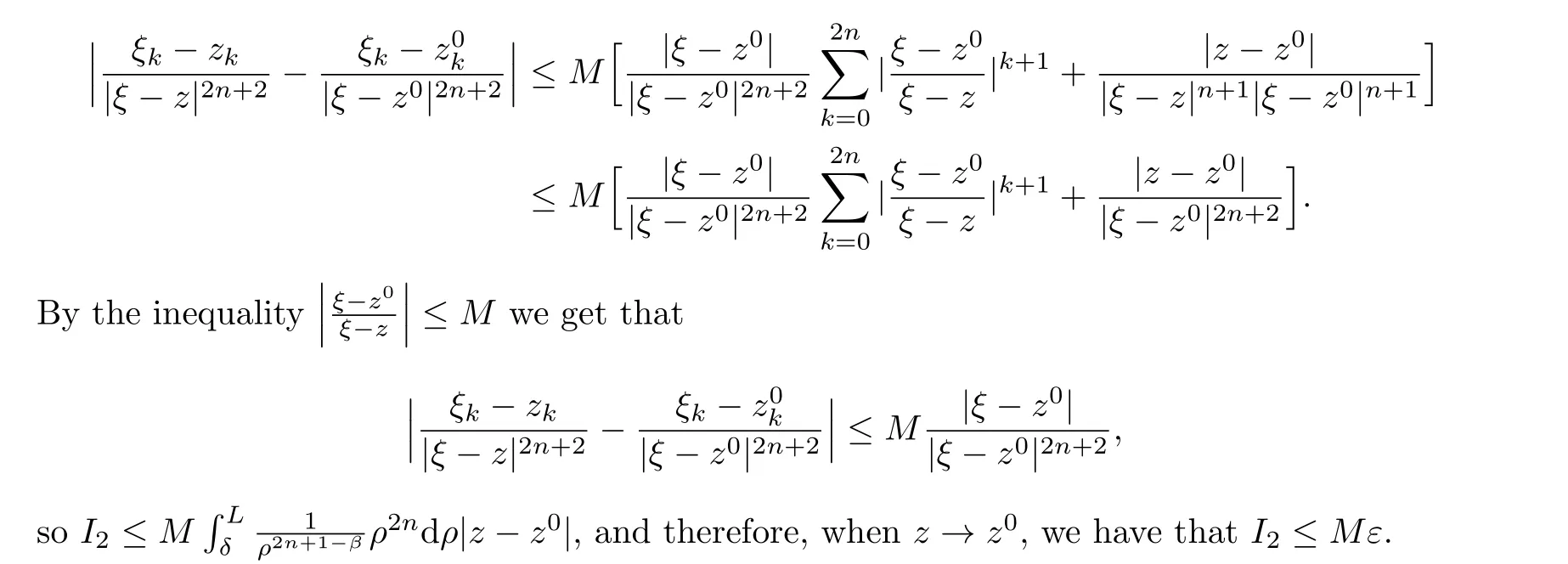
In summary, the conclusion holds whenz →z0is not in the direction of the tangent plane atz0∈∂Ω.

Case 2Suppose thatz →z0along the tangent plane atz0∈∂Ω.Chooseξ ∈∂Ω such that it satisfies|ξ-z|→0 and|ξ-z0|→0 at the same time.Since Ψ is uniformly continuous on∂Ω, for arbitraryε ＞0, we have that

when|ξ-z| and|ξ-z0| are small sufficiently.

Thus,|Ψ(z)-Ψ(z0)|≤|Ψ(z)-Ψ(ξ)|+|Ψ(z0)-Ψ(ξ)|≤ε.Therefore, the conclusion also holds along the direction of the tangent plane atz0∈∂Ω, whenz →z0.□

Theorem 3.6(Plemelj formula) Suppose that Ω,Uand∂Ω are as described in Theorem 3.1.Iff ∈H(β,∂Ω,Cl0,n(C)), then, for arbitraryz0∈∂Ω, we have that

Therefore,the equality(3.2)is established.From the equality(3.2),we can deduce that equality(3.3) is also established.□

4 H¨older Continuity of the Cauchy-type Integral

LetH(β,∂Ω,Cl0,n(C)) be the set of all H¨older continuous functions defined in∂Ω∈Cn+1with values in the Clifford algebraCl0,n(C).For anyf ∈H(∂Ω,β,Cl0,n(C)), we define that‖f‖β=C(f,∂Ω)+H(f,∂Ω,β), where

Theorem 4.1Letting Ω⊂Cn+1be a bounded domain,U ⊂Cn+1is a domain satisfying Ω⊂U, and the boundary∂Ω of Ω is a smooth compact orientable Liapunov surface.Iff ∈H(β,∂Ω,Cl1,n(C)), then Φ-f(z) isβ-H¨older continuous on∂Ω.

ProofTo prove that Φ-f(z) isβ-H¨older continuous, we just have to prove that there is a constantM19such that|Φ-f(z1)-Φ-f(z2)|≤M|z1-z2|β,(0＜β ＜1)holds,for anyz1,z2∈∂Ω.

Letting|z1-z2|=δ, construct a ballB(z1,3δ) withz1as the center and 3δas the radius.Then∂Ω is divided into two parts byB(z1,3δ).The part located on the surface∂Ω and inside the ballB(z1,3δ) is denoted asλ3δ, and outside the ballB(z1,3δ) is denoted as∂Ωλ3δ.To discuss the H¨older continuity,we need to consider that the conclusions can be established whenδ=|z1-z2| is small enough.Suppose that 6δ ＜d, wheredis the constant in the Liapunov surface definedd.Then,

Applying the generalized polar transformation toI1, we get that

Using a direct calculation, we obtain thatI32≤MH(f,∂Ω,β)|z1-z2|β.

Using a calculation similar as to that forI3, we get thatI4≤MH(f,∂Ω,β)|z1-z2|β.

To sum up, when 6|z1-z2|＜d, we have that

Proof From the definition of norm of a H¨older continuous function and Theorem 4.1, we get that

By Theorems 4.2 and 4.3, we get that

From Theorem 4.3 and Theorem 4.4, we have that

whereMis a constant independent off.□

Theorem 4.6 Letting Ω,∂Ω,Ω+= Ω be as stated above,‖Φf‖β ≤M‖f‖β, whereMis a constant independent off.

5 Linear Boundary Value Problem

Then

ProofBy direct calculation,we get that Φfis a complex right regular function inCn+1∂Ω.By Theorems 4.5 and 4.6, we can prove that (b) and (c) are true.□

Theorem 5.3Leta,b,g ∈H(∂Ω,β,Cl0,n(C)) and satisfy that

Letting 6δ ＜d,δ ＞0, wheredis a constant, construct a ballB(z,3δ) withzas the center and 3δas the radius, where the part of∂Ω is in the ballB(z,3δ) denoted asλ3δ, and the part of∂Ω is out the ballB(z,3δ) denoted as∂Ωλ3δ.Then

With regard toI1,

where

soFis a compression mappingT →T.There is a unique functionf ∈Tfrom the fixed point principle of the compression mapping such thatF(f)=f.

Hencefis the solution of equation (5.2), and Φfis the solution of Problem I, where

Conflict of InterestThe authors declare no conflict of interest.