THE INTERIOR TRANSMISSION EIGENVALUE PROBLEM FOR AN ANISOTROPIC MEDIUM BY A PARTIALLY COATED BOUNDARY*

(向建立)

Three Gorges Mathematical Research Center, College of Science, China Three Gorges University,Yichang 443002, China E-mail: xiangjianli@ctgu.edu.cn

Guozheng YAN (严I政)†

School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China E-mail: yangz@ccnu.edu.cn

Abstract We consider the interior transmission eigenvalue problem corresponding to the scattering for an anisotropic medium of the scalar Helmholtz equation in the case where the boundary ∂Ω is split into two disjoint parts and possesses different transmission conditions.Using the variational method, we obtain the well posedness of the interior transmission problem, which plays an important role in the proof of the discreteness of eigenvalues.Then we achieve the existence of an infinite discrete set of transmission eigenvalues provided that n ≡1, where a fourth order differential operator is applied.In the case of n /≡1, we show the discreteness of the transmission eigenvalues under restrictive assumptions by the analytic Fredholm theory and the T-coercive method.

Key words interior transmission eigenvalue; anisotropic medium; partially coated boundary; the analytic Fredholm theory; T-coercive method

1 Introduction

complex-valued scalar function such that Re(n)＞0 and Im(n)≥0.Then we can formulate the interior transmission problem as follows:

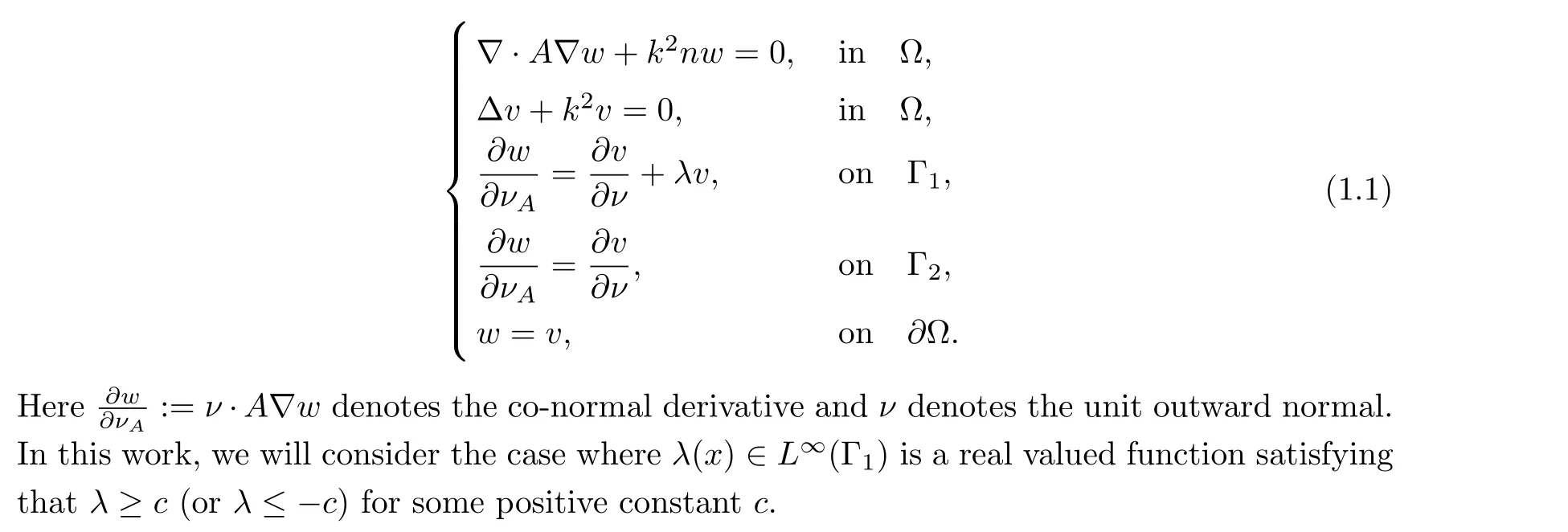
Definition 1.1Values ofk ∈C for which the homogeneous interior transmission problem (1.1) has a nontrivial solution pairw ∈H1(Ω) andv ∈H1(Ω) are called transmission eigenvalues.

The transmission eigenvalue problem is a class of non-selfadjoint eigenvalue problems that first appeared in inverse scattering theory for an inhomogeneous medium, and it is a boundary value problem for a set of equations defined in a bounded domain coinciding with the support of the scattering object.Due to the theoretical importance of transmission eigenvalues in connection with the uniqueness and reconstruction results in inverse scattering theory, the study of transmission eigenvalue problems has recently become an attractive research topic.

The first issueassociated with the interior transmission problem is concerned with the case of when the problem is well-posed.There are two main approaches: the boundary integral equation method and the variational method.For the sake of mathematical and computational interest,the boundary integral equation method has been applied to recover the solvability result of isotropic media when the refractive indexnis a positive constant different from one(refer to Section 3.1.4 in the book[8],and to the paper[19,25]).Since there are great limitations in terms of using the boundary integral equation method, the variational method has been widely used for both isotropic and anisotropic obstacles under different assumptions ([5, 6, 8, 11, 14, 26]).

The second issueconcerns the discreteness of transmission eigenvalues that we can avoid them in the procedure to reconstruct the boundary from far-field or near-field pattern.Based on the spectral theory of compact operators in Hilbert spaces(see Theorem 6.8 in the book[4]),the discreteness of eigenvalues for an isotropic medium has been shown in [2, 6, 8].When it comes to the anisotropic medium, we cannot construct a compact operator, so the analytic Fredholm theory (see Section 8.5 in the book [23]) is widely used.And there has been much work based on the analytic Fredholm theory under the caseλ= 0 on Γ1, which means that the boundary is integral (see [22, 23, 32] for the isotropic inhomogeneous medium, [7] for the anisotropic medium withn ≡1, [3, 5, 16] for general anisotropic media withn/≡1, [9] for regions with cavities,[10]for absorbing media,[12]for inhomogeneous media containing obstacles,[2,28,33]for the conductive boundary, etc).

The third and most difficult issueis whether there exist eigenvalues.The first result about the existence of transmission eigenvalues was obtained by Colton and Monk in 1989 for the case of a spherically stratified medium ([24]).Subsequently, McLaughliny used the knowledge of the transmission eigenvalues to determine a radial scatterer ([29, 30]).Until 2008, P¨aiv¨arinta and Sylvester ([31]) considered the general isotropic inhomogeneous scatterer without radial symmetry and showed that there exist a finite number of transmission eigenvalues provided that the index of refraction is large enough.Soon after in 2009, Cakoni and Haddar([15]) extended their ideas to present the existence of transmission eigenvalues for isotropic inhomogeneous media and also for anisotropic media withn ≡1.And in 2010, they studied a difficult case for regions with cavities ([9]).In the same year, the paper [13] proved the existence of an infinite discrete set of transmission eigenvalues for all of the above cases of the Helmholtz and Maxwell equations, and the paper [12] considered the case for inhomogeneous media containing obstacles.Furthermore, Cakoni and Kirsch ([17]) extended the investigation to the case of anisotropic media withn/≡1, where a fourth order differential operator is no longer applicable.Recently,more and more research has been done for more complicated media([1, 2, 18, 20, 27, 28]).

In this paper, we consider an anisotropic scatterer whose boundary is split into two parts and possesses different boundary conditions (refer to the problem (1.1) for details).Given this situation, the boundary loses its symmetry and some essential Poinc´are inequalities, which will be widely used in the proof, are difficult to obtain.Hence, we assume thatλ(x)is a real valued function satisfying thatλ ≥corλ ≤-cfor some positive constantc.And we only obtain the existence of infinite discrete eigenvalues under the casen ≡1 witha*＞1,λ ≤-cora*＜1,λ ≥c(Theorem 3.2 and Theorem 3.5).For the casen/≡1, we just show the discreteness result under the assumptions thata*＞1,n*＞1,λ ≤-cor 0＜a*＜a*＜1,0＜n*＜n*＜1,λ ≥c(Theorem 4.2), and the existence is an open problem that will require further investigation.

The rest part of this paper is organized as follows: in Section 2, we will consider the wellposedness of the interior transmission problem by the variational method.Section 3 is devoted to the discreteness and existence of the transmission eigenvalues forn ≡1 where a fourth order differential operator is applied.In Section 4, we use the analytic Fredholm theory and the T-coercive method to investigate the discreteness of the transmission eigenvalues forn/≡1.

2 The Well-posedness of the Interior Transmission Problem

In this section, we establish the well-posedness of a more general interior transmission problem associated with (1.1); that is, givenℓ1∈L2(Ω),ℓ2∈L2(Ω),f1∈H-1/2(Γ1),f2∈H-1/2(Γ2) andf3∈H1/2(∂Ω), findw ∈H1(Ω) andv ∈H1(Ω) satisfying that

Note thatH-1/2(Γj):={ f|Γj:f ∈H-1/2(∂Ω)}and the norm is defined by‖～f‖H-1/2(Γj):=inf{ ‖f‖H-1/2(∂Ω)forf ∈H-1/2(∂Ω),f|Γj= ～f }(j= 1,2).Here and below, all notations possess the same meaning as defined in the introduction.We also make the following new notations:

To investigate the solvability of problem (2.1), we need to formulate a modified interior transmission problem (2.2), which turns out to be a compact perturbation of our original problem(2.1).Introducing a positive constantγwhose value will change in different cases,given two functionsℓ1∈L2(Ω),ℓ2∈L2(Ω) and boundary dataf1∈H-1/2(Γ1),f2∈H-1/2(Γ2),f3∈H1/2(∂Ω), findw ∈H1(Ω) andv ∈H1(Ω) satisfying that

The next theorem states the equivalence between problems (2.2) and (2.3); the detailed proof is the same as Theorem 3.3 in the paper [6] and Theorem 6.5 in the book [5], so we omit the proof for brevity.

Theorem 2.1The problem (2.2) has a unique solution (w,v)∈H1(Ω)×H1(Ω) if and only if the problem (2.3) has a unique solutionU=(w,v)∈H1(Ω)×W1(Ω).

Now we investigate the modified interior transmission problem in the variational formulation(2.3).

Theorem 2.2Assume thata*＞1,γ ≥a*andλ ≤-con Γ1.Then the variational problem (2.3) has a unique solutionU=(w,v)∈H1(Ω)×W1(Ω) which satisfies that

whenceA1is coercive.The detailed procedure to obtain the last inequality can be found in the paper [6] (Theorem 3.4) or in the book [8] (Lemma 3.30).The continuity ofA1follows easily from Schwarz’s inequality and the classical trace theorems.Theorem 2.2 is now a direct consequence of the Lax-Milgram Lemma applied to (2.3).□

Second, we consider the casea*＜1 andλ ≥con Γ1.To gain a different equivalent variational form, we define another Hilbert space

Theorem 2.3The problem (2.2) has a unique solution (w,v)∈H1(Ω)×H1(Ω) if and only if the problem (2.4) has a unique solution U=(w,v)∈W2(Ω)×H1(Ω).

Theorem 2.4Assume thata*＜1,a*≤γ ＜1 andλ ≥con Γ1.Then the variational problem (2.4) has a unique solution U=(w,v)∈W2(Ω)×H1(Ω) which satisfies that

On the other hand, if U=(w,v)∈W2(Ω)×H1(Ω), the assumptions thata*＜1,a*≤γ ＜1 andλ ≥cimply that

whenceA2is coercive.The proof is completed.□

Summarizing the above analysis,we can state the following result concerning the solvability of the interior transmission problem (2.1):

Theorem 2.5Assume that eithera*＞1,λ ≤-cora*＜1,λ ≥c, and thatkis not a transmission eigenvalue of the problem (1.1).Then the general interior transmission problem(2.1) has a unique solution (w,v)∈H1(Ω)×H1(Ω) which satisfies that

withC ＞0 dependent on‖λ‖L∞(Γ1).

The proof is completely the same as Theorem 3.6 in the paper [6] and Theorem 3.32 in the book [8], so we omit it here.

Remark 2.6Note that we obtain the well-posedness of the problem (2.1) under the special condition that the sign ofλhas a close relation with the value ofA.Consequently,in the following sections, we keep the assumptions of Theorem 2.5 above.And in the future,we want to discard this strict restriction onλor even consider thatλ(x) is a complex valued function.

Before we study the transmission eigenvalue problem(1.1),we first establish the uniqueness of a solution to (2.1), i.e., there are no transmission eigenvalues.

If Im(n)＞0 almost everywhere in Ω, thenw= 0 in Ω.Similarly, from the boundary condition in (2.1) and the integral representation formula,valso vanishes in Ω.The proof is complete.□

3 The Transmission Eigenvalues for n ≡1

In this section, we study the discreteness and existence of the transmission eigenvalues under the special casen ≡1, where we can obtain a fourth-order equation.Here we assume that Im(A) = 0 and eithera*＞1,λ ≤-cor 0＜a*＜1,λ ≥c.Then the transmission eigenvalue problem forn ≡1 reads as

withv ∈H1(Ω) andw ∈H1(Ω).We make the following substitutions:

Theorem 3.1Let Λ1(Ω)be the first Dirichlet eigenvalue of-Δ in Ω.Then the following hold:

1.fora*＞1 andλ ≤-con Γ1, real wave numbersk ＞0 such thatk2＜Λ1(Ω) are not transmission eigenvalues;

2.fora*＜1 andλ ≥con Γ1, real wave numbersk ＞0 such thatk2＜a*Λ1(Ω) are not transmission eigenvalues.

ProofFirst,we recall that for∇·u∈H10(Ω),using the Poincar´e inequality,we have that

and consider the operatorFkfromH(Ω)intoL2(Ω)×L2(Ω)×H-1/2(Γ1)×H-1/2(Γ2)×H1/2(∂Ω)defined by

Since (Fκ-Fk)(w,v)=((κ2-k2)nw,(κ2-k2)v,0,0,0) is compact based on the compact embedding ofH1(Ω) toL2(Ω), we conclude that the transmission eigenvalues are discrete by the analytic Fredholm theory (see Section 8.5 in the book [23]).The proof is complete.□

The following theorem provides the theoretical basis of our analysis regarding the existence of transmission eigenvalues (refer to Theorem 6.15 in the book [5] or Theorem 4.5 in the book[8]):

Theorem 3.3LetAδbe a continuous mapping from(0,+∞)to the set of bounded,self-adjoint, and coercive operators on the Hilbert spaceXand let B be a self-adjoint and nonnegative compact bounded linear operator onX.We assume that there exist two positive constantsδ0＞0 andδ1＞0 such that the following hold:

1.Aδ0-δ0B is positive onX;

2.Aδ1-δ1B is nonpositive on anℓ-dimensional subspaceWjofX.

Then each of the equationsλj(δ) =δforj= 1,···,ℓhas at least one solution in [δ0,δ1]whereλj(δ)is thej-th eigenvalue(counting multiplicity)of Aδwith respect to B, i.e., ker(Aδλj(δ)B)/={0}.

To investigate the existence of eigenvalues for the problem (3.1), we need to consider the classical transmission eigenvalue problem for a ballBρof radiusρcentered at the origin with a constant index of refractionm ＞0 andm/=1, which is formulated as

Theorem 3.5Assume thatn ≡1,Im(A)=0 anda*＞1,λ ≤-cora*＜1,λ ≥c.Then there exists an infinite set of real transmission eigenvalues for the anisotropic medium problem(3.1) with +∞as the only accumulation point.

ProofBased on the Lemma 3.4,we need only to prove the Assumption 2 in Theorem 3.3(refer to Theorem 6.20 in [5] or Theorem 4.12 in [8]).

This means that Assumption 2 of Theorem 3.3 is also satisfied, and therefore we conclude that there areM(ε) transmission eigenvalues (counting multiplicity) inside [δ0,δ1].Note thatM(ε) andkε,a-1*both go to +∞asε →0.Since the multiplicity of each eigenvalue is finite,we have shown, by lettingε →0, that there exists an infinite countable set of transmission eigenvalues that accumulate at +∞.

The proof of the second case is the same, so we omit it for brevity.□

4 The Discreteness of Transmission Eigenvalues for n/≡1

In this section, we only consider the discreteness of transmission eigenvalues (1.1) for the general casen/≡1.Based on Theorem 2.7, we assume that Im(A) = 0, Im(n) = 0, and we introduce the notations

We observe thatkis a transmission eigenvalue to(1.1)if and only if there exists a non-trivial element (w,v)∈Xsuch that

Similarly to Section 3, we want to find ak ∈C such thatGkis invertible.However, differently from the classical form, we find thatak(·,·) is not coercive for anyk ∈C.Hence, we will use the T-coercive method ([3, 21]) to show thataiκ(·,·) is T-coercive forκ ∈R{0}.

Theorem 4.1Assume that eithera*＞1,n*＞1,λ ≤-cora*＜1,n*＜1,λ ≥c.Then there existsk=iκwithκ ∈R{0}such that the operatorGkis invertible.

ProofFor the first casea*＞1,n*＞1,λ ≤-c, we consider the mappingT:X-→Xdefined byT:(w,v)-→(w,-v+2w).Note thatT2=I, and henceTis an isomorphism inX.

Then for all (w,v)∈X, we have that

For the second case 0＜a*＜a*＜1, 0＜n*＜n*＜1 andλ ≥c, the isomorphism mappingT:X-→Xis defined by

Similarly, we will used the following two inequalities:

Consideringκ0∈R{0}, thenGiκ0is invertible.SinceGk-Giκ0is a compact operator for allk ∈C, using the analytic Fredholm theory (see Section 8.5 in the book [23]), we deduce the following theorem:

Theorem 4.2Assume that eithera*＞1,n*＞1,λ ≤-cor 0＜a*＜a*＜1,0＜n*＜n*＜1,λ ≥c.Then the transmission eigenvalues of (1.1) form a discrete (possibly empty) set in C with +∞as the only possible accumulation point.

Remark 4.3For the casen/≡1 andA/≡I(Iis the identity matrix), we only obtain the discreteness under the assumption thata*＞1,n*＞1,λ ≤-cor 0＜a*＜a*＜1,0＜n*＜n*＜1,λ ≥c.The discreteness for weaker assumptions and the existence of eigenvalues are open problems.

Remark 4.4In this paper, we consider two cases:A/≡I,n ≡1 andA/≡I,n/≡1.For the third case,A ≡I,n/≡1, the discreteness and existence of transmission eigenvalues can be achieved by the same procedure as in the paper [2] where the boundary is integral.

Remark 4.5If Ω⊂R3simply connected and∇×v= 0 in Ω, then there exists a potentialpsuch thatv=∇p.Based on this fact, the results in this paper can be extended for the 3-dimensional case.

Conflict of InterestThe authors declare no conflict of interest.