基于流固耦合的输水隧洞水平旋喷拱棚挠度影响因素研究

王显

（沧州水利勘测规划设计院有限公司，河北 沧州 061000）

1 研究背景

水利工程建设对优化水资源配置，充分发挥有限水资源的价值具有十分重要的作用和意义。基于此，我国各级政府不断加大在水利工程建设领域的投入力度，建设了一大批复杂地质环境条件下的输水工程。在长距离输水工程中，输水隧洞往往是不可或缺的重要组成部分。在长距离输水隧洞建设中，经常需要穿越河谷地带，从而面临浅埋富水砂软弱地层，给工程建设的顺利进行带来诸多困扰。因此，在穿越上述地层的输水隧洞施工过程中，需要采用一定的辅助措施对围岩进行预支护。水平旋喷技术是地下洞室工程中常用的预支护手段，通常沿地下洞室的洞口周边以外插的方式分布和咬合，从而形成拱棚预支结构，该方式十分适合富水砂性地层地下洞室工程的预支护，可以有效缓解涌水、涌沙地质灾害[1]。

虽然超前水平旋喷预支护技术在富水砂性地层的地下工程建设中得到广泛应用，显示出相对于超前小导管注浆等传统预支护方式的优越性[2]，但是，其成桩工程效果受到施工工艺、地质环境等诸多因素的影响，进而影响其支护效果。目前，业界关于水平旋喷拱棚的受力特征与变形规律研究尚不完善，导致工程实践应用缺乏必要的理论依据，从而限制了该加固方式的推广和应用[3]。基于此，此次研究以某输水隧洞穿越河谷段工程为依托，利用数值模拟的方式探讨输水隧洞水平旋喷拱棚挠度的变化规律，以便为相关研究和工程实践提供必要的支持和借鉴。该段输水隧洞为马蹄形断面设计，其宽度和高度分别为4.5 m 和4.8 m，水平旋喷拱棚桩的桩径为0.5 m，相邻桩中心距为3.5 m，共需要设置25 根水平旋喷桩。

2 模型计算

2.1 有限元模型的构建

此次研究利用FLAC3D 有限元软件进行数值计算模型的构建[4]，利用上、下台阶法模拟隧洞的开挖过程[5]。为了有效消除模型边界效应可能对计算结果产生的影响，模型的横向尺寸为隧洞宽度的10 倍，下部深度为拱底向下5 倍的隧洞高度，模型上部模拟至地表，最终确定模型尺寸为45.0 m×40.0 m×50.0 m。

为保证计算精度，模型的网格划分系数取0.5，对隧洞开挖岩土体、水平旋喷拱棚及衬砌结构等关键部位进行加密处理[6]。考虑到对水平旋喷拱棚和周围岩土体采用共节点的计算方式会导致拱棚和土层之间的协同变形，从而产生较大的计算误差，因此，计算中应考虑旋喷桩和岩土体的接触效应，利用界面单元解决上述问题。界面单元可以有效提升有限元网格的柔性，防止非物理应力结果的出现，保证计算结果的精确性[7]。此次研究模型划分为21 246 个单元，22 357 个节点。

2.2 边界条件和计算参数

考虑到河谷内地表水和地下水均十分丰富，因此，在模型计算过程中将各种介质均设置为饱和状态，且保持水位高度不变[8]。模型采用软件中提供的完全流固耦合方法进行管棚轴力和挠度的计算。隧洞围岩岩土体采用实体单元模拟，其中，围岩采用小应变硬化本构模型，水平旋喷拱棚和初衬采用弹性本构模型，并将其设置为不透水材料。隧道的开挖断面设置为透水边界，水压力初始值设定为0。

模型材料参数是影响计算结果的重要因素，研究中以背景工程的地质勘查资料和相关施工规范为依据确定模型材料物理力学参数，如表1所示。

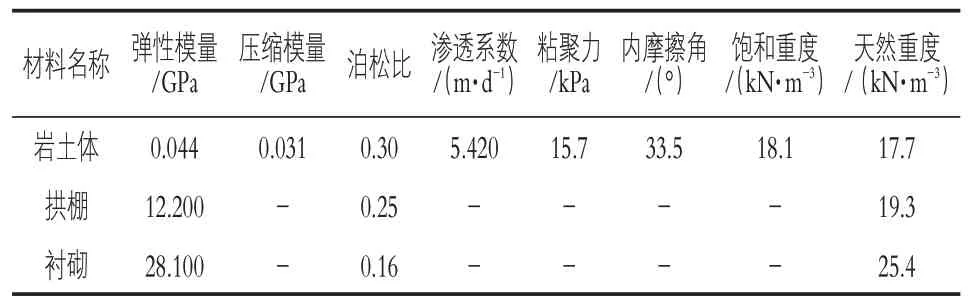
表1 模型材料物理力学参数

2.3 计算方案

结合背景工程实际和相关研究成果，本文选择地层渗透系数、地下水位和隧洞埋深等因素进行计算分析。地层渗透系数分别设置为50.000，5.000，0.500，0.050，0.005 m/d；地下水位设置为0（拱顶部位），1.0，2.0，3.0，4.0 m；隧道埋深设置为7.0，9.0，11.0，13.0，15.0 m。研究中固定两个参数值不变，以挠度为表征量，对第3 个参数不同取值条件下水平旋喷拱棚的力学特征进行模拟计算。

3 计算结果与分析

3.1 地层渗透系数

研究中保持地下水水位2.0 m、隧道埋深11.0 m不变，利用构建的有限元模型对不同地层渗透系数条件下水平旋喷拱棚的挠度进行模拟计算，从计算结果中提取出上台阶开挖进尺为10.0 m 时拱棚拱顶部位的桩体挠度，并绘制出变化曲线，见图1。由图1 可知，随着地层渗透系数的减小，拱顶部位的挠度最大值呈现出不断增大的变化特点，且挠度的最大值出现在施工开挖掌子面的后方附近；挠度并非随着地层渗透系数的减小呈现线性变化，当渗透系数减小到一定值时，挠度增长较为有限，究其原因，主要是水平旋喷桩拱棚可以发挥显著的预支护作用，使拱棚上部的地下水难以形成竖向渗流，只能通过水平方向进行渗流，而地层渗透系数的减小会抑制渗流作用的发生，导致水平旋喷拱棚的挠度增大。

图1 不同地层渗透系数挠度变化曲线

3.2 地下水位

研究中保持地层渗透系数0.500 m/d、隧道埋深11.0 m 不变，利用构建的有限元模型对不同地下水位条件下水平旋喷拱棚的挠度进行模拟计算，从计算结果中提取出上台阶开挖进尺为10.0 m 时拱棚拱顶部位的桩体挠度，并绘制出变化曲线，见图2。由图2 可以看出，在不同地下水位工况下，水平旋喷拱棚拱顶部位桩体的挠度变化规律基本一致，均呈现出先增大后减小并逐渐趋于稳定的变化趋势，挠度的最大值出现在施工开挖掌子面后方附近；随着地下水水位的升高，水平旋喷拱棚拱顶部位桩体的挠度呈现出不断增大的变化趋势，且地下水位越高，其对挠度的影响越大，由此可见，地下水水位对拱顶部位水平旋喷桩的挠度影响较大。为保证隧洞施工安全进行，对于地下水水位较高的洞段，建议采取增加旋喷桩桩径、桩间咬合厚度及注浆浆液强度的工程措施，同时，还应该加强施工掌子面的防渗处理。

图2 不同地下水位挠度变化曲线

3.3 隧洞埋深

研究中保持地层渗透系数0.500 m/d、地下水位2.0 m 不变，利用构建的有限元模型对不同隧洞埋深条件下水平旋喷拱棚的挠度进行模拟计算，从计算结果中提取出上台阶开挖进尺为10.0 m 时拱棚拱顶部位的桩体挠度，并绘制出变化曲线，见图3。由图3 可以看出，在不同隧洞埋深条件下，水平旋喷拱棚拱顶部位桩体的挠度变化规律基本一致，均呈现出先增大后减小并逐渐趋于稳定的变化趋势；挠度的最大值出现在施工开挖掌子面后方附近；随着隧洞埋深的增加，水平旋喷拱棚拱顶部位桩体的挠度呈现出不断增大的变化趋势，且增大的趋势表现出比较显著的线性特征，究其原因，主要是地下水位不变的情况下，隧洞埋深的增大会导致拱棚上部岩土体压力和地下水作用的稳步增加，旋喷桩挠度也呈现出不断增大的变化特点。因此，对于埋深较大的洞段也需要采取上文提出的工程措施，保证施工安全。

图3 不同隧洞埋深挠度变化曲线

4 结语

此次研究以具体工程为依托，利用数值模拟的方式探讨和分析了输水隧洞水平旋喷拱棚挠度影响因素及相关规律，并提出了具体的工程建议，研究结论本身对相关理论研究和工程设计具有重要的支持和借鉴作用。当然，此次研究在水平旋喷拱棚成桩效果良好的前提下展开，没有探究桩体缺陷的影响，也没有考虑水平旋喷拱棚出现漏水情况对自身受力特征的影响。显然，上述情况在工程施工中往往是不可避免的。因此，在今后的研究中需要针对上述情况进行进一步的分析研究，以获得更为全面和准确的研究成果。