利用对偶图形计算河流断面面积方法初探

董海涛，张常俊，刘晓凤

（1.黑龙江省水文水资源中心哈尔滨分中心，黑龙江 哈尔滨 150010；2.黑龙江省水文水资源中心，黑龙江 哈尔滨 150001）

0 引言

水文数据是国家重要的基础信息资源，在防汛抗旱、防灾减灾、水资源可持续利用、水利工程设计和社会经济可持续发展中有着重要的作用。流量数据是水文数据的重中之重，流量计算的一个重要参数就是河流断面面积。实际的天然河道断面非常复杂，断面线也复杂多变，一般情况下，几乎不可能直接利用其断面曲线计算面积，所以通常是以折线代替曲线，并概化成梯形进行河道断面面积的计算[1]，这也就导致了通过有限的测深垂线计算的断面面积存在偏小或偏大的现象。当然，这种现象可通过增加测深垂线数量以满足要求，但在实际当中会耗费大量的人力、物力。

为了提高断面面积的计算精度，除了增加测深垂线，还可以从计算方法上去探寻解决办法。本文以呼兰河兰西站为实际算例，引进对偶图形[2]，通过外切多边形进行面积计算，以提高断面面积计算精度，减少面积误差对流量的影响。

1 对偶图形方法的简介

在射影几何里，把点和直线叫做对偶元素，把“过一点作一直线”和“在一直线上取一点”叫做对偶运算[2]。在射影平面上，把由点和直线所组成的一个图形中的各元素改为它的对偶元素，各运算改为它的对偶运算，结果就得到另一个图形，这两个图形称为对偶图形。

在河流断面面积计算[3]中，水道河床断面线是一条曲线，通常以有限的测点连接成一条折线来代替曲线（见图1 实测线）。通过对偶计算，将此曲线通过测点的切线组成另一条折线以代替曲线（见图1 切折线），这两条折线就是对偶图形。为方便起见，称以实际测点连接的折线为点折线，以切线段组成的折线为切折线。

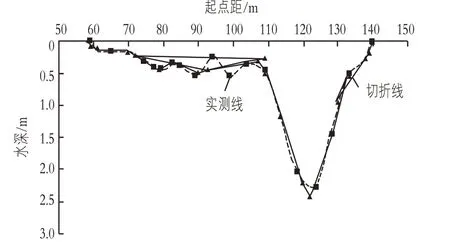
图1 呼兰河兰西断面切折线与实测点断面图

只用一条折线去代替曲线，且以有限的测点计算面积，面积偏大或偏小的概率非常大。以连续上凹断面为例，常规面积计算是利用内接多边形从一侧逼近曲线断面面积的真实值。对偶面积计算方法则是利用外切多边形，从另一侧逼近曲线断面面积。

2 断面面积的计算

一般地，河流断面线是一条曲线，有的呈现窄深形，有的呈现起伏变化的宽浅形，还有的是两种或更多种叠加形等，断面线的变化用起点距和水深/高程两个变量以函数的形式表示。

2.1 点折线面积的计算

由于断面线复杂多变，几乎无法找到具体的函数表达式，这就使得通过曲线的形式来计算断面面积的方式难以实现。在实际应用中，只能通过有限的实测点数据绘制点折线代替曲线，并概化成梯形来计算河道断面面积，这是目前面积计算普遍使用的方法。

2.2 切折线面积的计算

由于断面线复杂、测点有限，在做实测点切线时，取实测点左右相邻两点的连线为切线方程的斜率，再代入切点得出切线方程[4]，具体方法如下。

根据已知起点距和相应水深的实测数据，令一个断面起点距即横坐标x为x0，x1，x2，x3，……，xn-1，xn，xn+1，其对应的纵坐标y（水深）为y0，y1，y2，y3，……，yn-1，yn，yn+1，则除两个边点（x0，y0）（xn+1，yn+1）外，建立其他各测点（xi，yi）处的切线方程：

式中：yi为第i点水深，m；xi为第i点起点距，m；f′(xi)为第i点处切线斜率。

利用拉格朗日中值定理，以曲线某一个点前、后相邻的两个点连线作为该点曲线切线的平行线，求得各点曲线的切线斜率ki：

式中：yi+1，yi-1分别为第i+1、第i-1 测点的起点距，m；xi+1，xi-1分别为第i+1、第i-1 的测点水深，m。

由式（2）和式（3）求各切线截距：

式中：hi为通过第i测点切线的截距，m。

由式（3）和式（4）计算出每条切线方程中的截距和斜率，就可以确定通过曲线上各个测点的切线方程。相邻两切线交点利用下列方程组求得：

因为两岸水边点仅有一点，无法计算出斜率，从而无法确定切线，故原水边点仍作为切折线的水边点，而过该点与相邻切线的交点由以下方程求得：

由式（5）（6）（7）即可求得切折线的交点，从而得出切折线图形。

3 方法的改进

对于连续上凹的水道断面，利用相邻切线交点求得起点距和水深能够达到预期效果，而实际上，天然河流断面曲线变化起伏不定、非常复杂，并非是一个连续上凹的曲线，且测点高低变化不均匀，使得相邻两切线相交不在两个切点之内，导致切折线杂乱无序（见图1 切折线），利用切线相交无法得到预期效果，因而采用切线段的方式来取得切折线。取相邻两实测点起点距的平均值作为切折线的切线段端点的起点距，分别带入两实测点对应的切线方程，得其相应水深。由于相邻切线段同一起点距的两端点处水深不等，会出现两个数值，致使切折线不相交，无法形成连续的断面图，采用将两端点垂直连接的方法可以得到一个间断式的切折线（见图2 改进的切折线）。

4 面积计算实例

4.1 单次大断面计算

运用改进的切折线方法，选取该站测深线间距不是均匀相等的测次断面进行面积计算，并与点折线断面面积计算值进行比较，其中，点折线计算结果为59.8 km2，切折线计算结果为60.3 km2，相对误差为0.8%。

图2 呼兰河兰西断面改进的切折线与点折线图

4.2 多次大断面计算

选取该站畅流期共58 次流量断面面积计算成果，并与原有断面面积进行比较：相对误差为正有8 次，占总测次的14.0%；相对误差为负有5 次，占总测次的9.0%；相对误差为零有45 次，占总测次的77.0%；最大相对误差的绝对值不超1.0%，满足断面面积误差限（±3.0%）的规定。从相对误差为正的稍多于负的可以说明，该断面线虽然起伏变化，但上凹比重稍大。

5 结语

文中引进了对偶图形计算河流断面面积，在同一断面及相同测深垂线条件下，对偶面积计算方法较常规方法精度更高，可以减少面积误差对流量的影响。在实际工作中，该方法能够代替使用加倍测深垂线数的方式来检验测深垂线数目布设的合理性，从而减少日常工作量。