基于SWAN 模型下的马拉博油罐区深水波浪条件分析
2024-03-21李会兴张杰峰李子成
李会兴,张杰峰,李子成
(中国路桥工程有限责任公司,北京 100011)
引言
深水区域的波浪和风环境是海洋工程和海岸管理中极其重要的因素之一,该领域的研究对于提高海洋工程和海岸管理的效率和准确性都有着重要的作用[1]。相关领域的学者和工程师们一直在进行大量的研究和实验,并在数值模拟、试验研究和实场测量等多个方面已经取得长足的进展。
Ris 等[2]总结了历年来波浪能量输入、损耗及转换的研究成果,提出并发展了适用于海岸和河口地区的SWAN 浅水波浪数值模拟模型并进行了验证。近年来的最新研究成果合理地计入了浅水波浪破碎及非线性效应,Battjes[3]、Cavaleri[4]和Collins[5]都对此进行了大量的研究,使该模型更适用于破碎波的数值模拟。Rogers 等[6]采用S&L 和SORDUP两种新的数值计算方法,进一步减少了模式在应用于较大尺度海域时所产生的数值耗散。
本文基于第三代海浪数值模型 SWAN,以CCMP 和CFSR 数值风场为驱动,对1979 年~2014年南大西洋的波浪进行了逐年后报。基于该项数据,分析了几内亚湾周边工程外海的极值波浪条件,并与已有极值波浪条件分析成果进行了综合比较,检验了该项数据的合理性。并以“赤道几内亚马拉博油罐区项目”为例,分析了风况与波浪条件,图1 为分析点(BE 站和GEW 站)与工程区位(PBN和PGE)的位置关系。
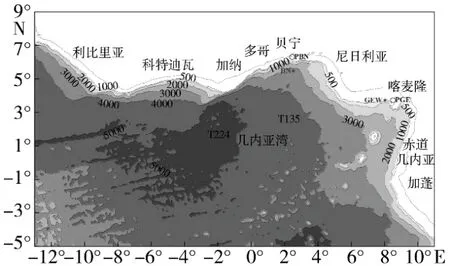
图1 几内亚湾水陆形势、工程区位以及深水波浪要素分析点位图Fig.1 The map of water and land situation,engineering location,and deepwater wave elements analysis points in the Gulf of Guinea
1 波作用量平衡方程数值模拟模型
1.1 波作用量平衡方程
SWAN 以二维作用量密度表示随机波,作用量密度N(σ,θ)与能谱密度E(σ,θ)之间关系为N(σ,θ)=E(σ,θ)。在笛卡尔坐标系下,作用量平衡方程可表示为:
方程左边第一项为N随时间的变化率;第二和第三项表示作用量密度在地理坐标空间x、y方向上的传播;第四项表示由于流场和水深所引起的作用量密度在相对频率σ空间的变化;第五项表示作用量密度在谱分布方向θ空间的传播,亦即水深及流场而引起的折射;c代表在不同方向或空间中的波速;方程右边的S代表以谱密度表示的源汇项,包括风能输入、白浪、破碎、海底摩擦、波—波非线性相互作用等物理过程。
在球坐标系下,作用量平衡方程可表示为:
其中 λ 是经度,φ 是纬度。
1.2 物理过程的处理
SWAN 模型对能量输入、耗散和非线性波波相互作用等物理过程的处理方法如下:
1)风能输入
根据Philips 的共振机制和Miles 的切流不稳定机制,将风能输入分为线性增长和指数增长两部分:Sin(σ,θ)=A+BE(σ,θ),其中A代表线性成长部分,B代表指数成长部分。
2)海底摩擦
海底摩擦引起的能量消耗与底床构成、糙率尺度、沙纹高度等因素有关,底摩阻耗散可表示为:
3)水深变浅引起的波浪破碎
室内试验和现场观测表明,当初始单峰波谱向浅水处传播时,波谱保持相似性,所以水深变浅引起的破碎总能量可以表示如下:
其中,E(σ ,θ )为总波能;D(σ ,θ )为总波能耗散率,与破波参数γ=Hmax(Hmax为在当地水深d时随机波中最大可能单个波高)密切相关。
4)白浪损耗
关于白浪引起的能量消耗,SWAN 模型采用的是Hasselmann(1974)脉动模式。
5)非线性波—波相互作用
在SWAN 模型中,对四波非线性相互作用的处理采用的是Hasselmann(1985)[7]离散迭代近似模型(DIA);对三向波相互作用的处理,采用的是Edeberky(1995)集合三相近似模型(LTA)。
6)波浪的绕射
Holthuijsen 和Booij(2003)[8]提出了以缓坡方程为理论基础的相解藕的方法,当考虑绕射的影响时,地理空间和谱空间的传播速度可表示为:
2 南大西洋1979~2014 年海浪数值后报
2.1 模型计算范围和参数选择
南大西洋海浪数值后报模型基于第三代海浪数值模式SWAN建立,模型计算的空间范围为60 °S~20 °N,60 °W~20 °E,向南包括西风带,空间网格步长为15′ × 15′,时间步长为10 min。在二维谱空间的分辨率上,频率的计算从0.03~2.0 Hz,以对数分布划分为34 个;方向分段为45,分辨率为8.0 °。在模型的物理机制上,风能的输入考虑线性增长和指数增长两部分,白浪损耗采用Komen 公式;四相波非线性相互作用采用Hasselmann 离散迭代近似模型,计算参数采用相关模式的建议值。
2.2 南大西洋海浪数值后报效果检验
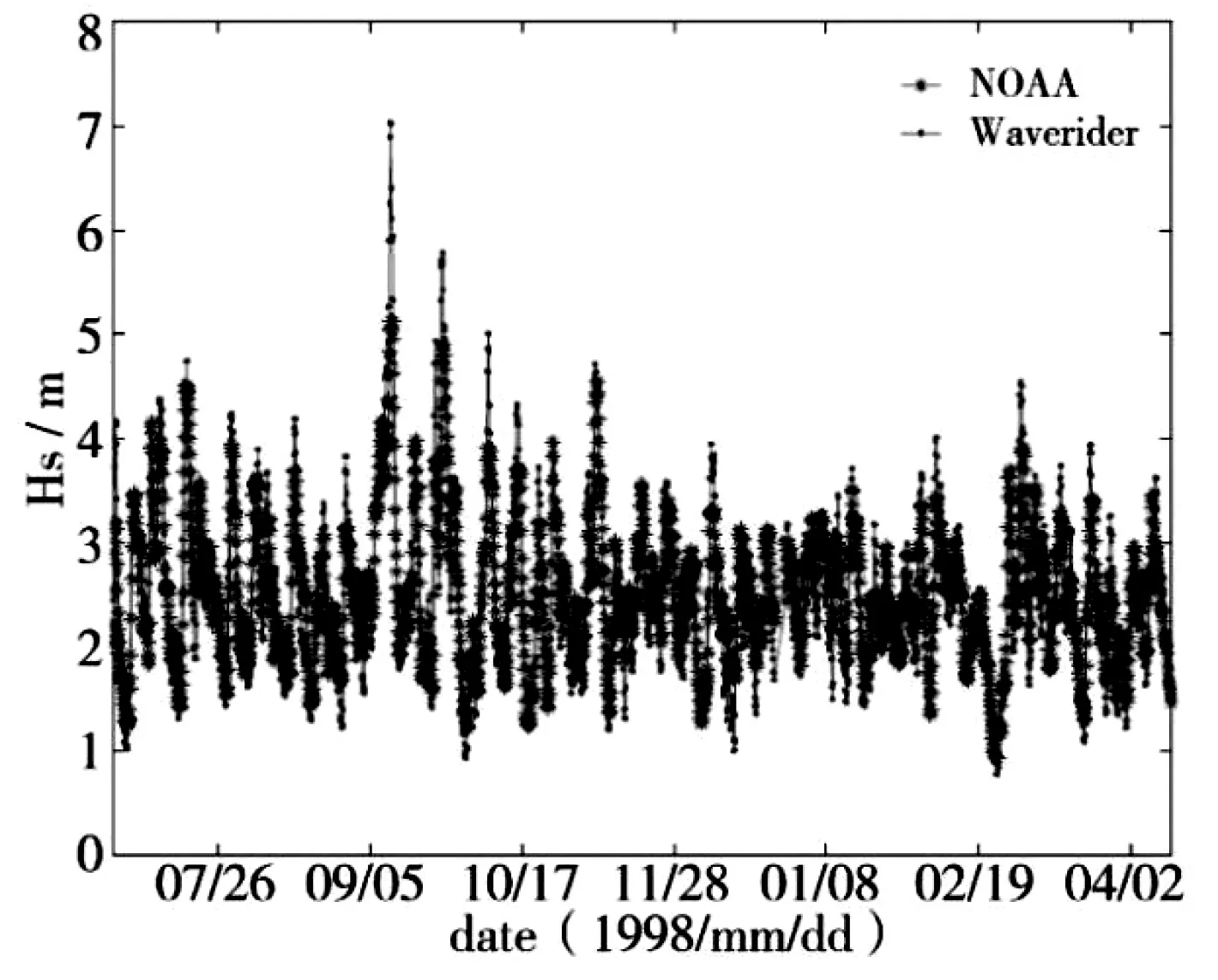
图2 Kudu 站1998 年06 月27 日~1999 年04 月13 日有效波高的时间变化Fig.2 Diagram of the variation of significant wave height over time at Kudu Station from June 27,1998 to April 13,1999
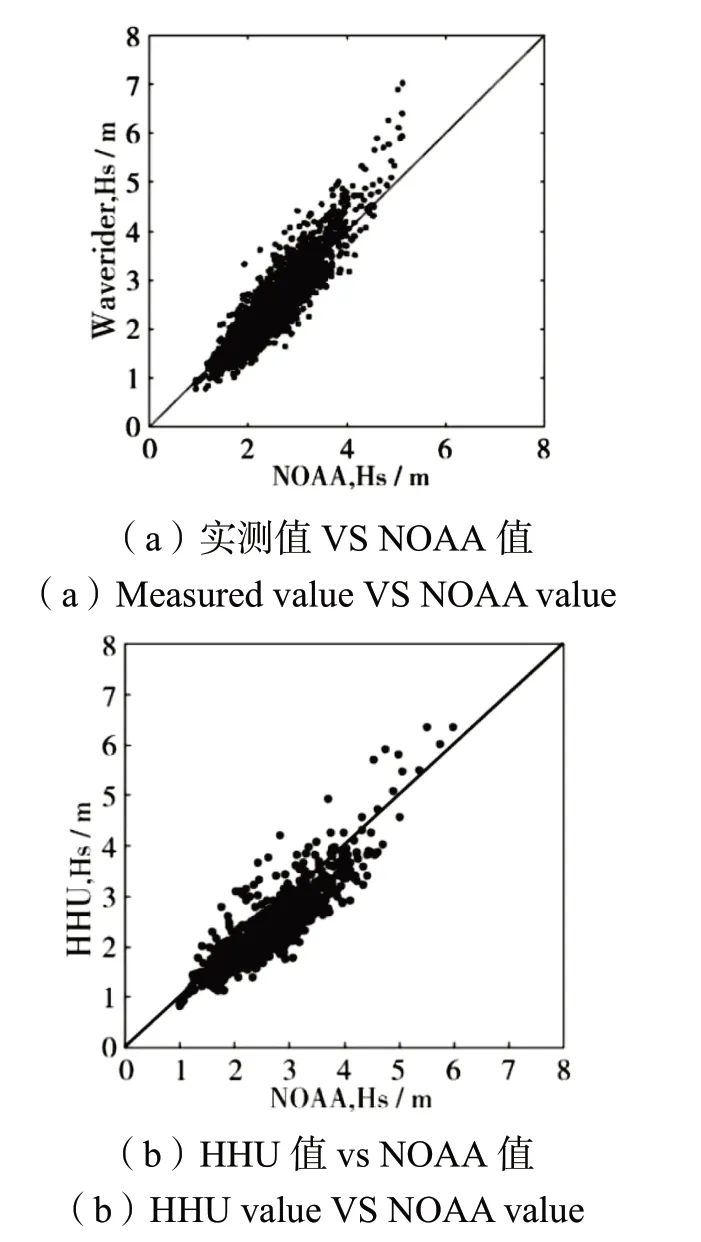
图3 Kudu 站不同数据源有效波高的散点分布Fig.3 Scatter distribution of significant wave heights form different data sources at Kudu station
表1对本文有效波高后报结果与NOAA全球海浪后报结果进行了定量的比较,给出了NOAA 值和本文值得均值偏差、均方根偏差和相关系数。

表1 本文有效波高计算值与NOAA 值的定量比较Tab.1 Quantitative comparison between the calculated significant wave height in this article and the values of NOAA
定量比较结果显示:本文有效波高后报结果与NOAA 后报值较为一致:在几内亚湾Bonga 站的三次测量期间,二者有效波高的相关系数在0.72~0.84,均值偏差在0.10~0.29 m,均方根偏差在0.25~0.41 m;在纳米比亚外海Kudu 站历时15 个月的波浪观测期间,二者有效波高的相关系数为0.86,均值偏差为-0.34 m,均方根偏差为0.45 m。
3 深水波浪条件分析
3.1 风
1)数据源
据CCMP 和CFSR 数值风场资料,提取了马拉博外海GEW 站(地理位置如前文图1 所示)1979年~2014 年风速的时间变化过程,如图4 所示。图5 给出了极坐标系下风速、风向的散点分布。
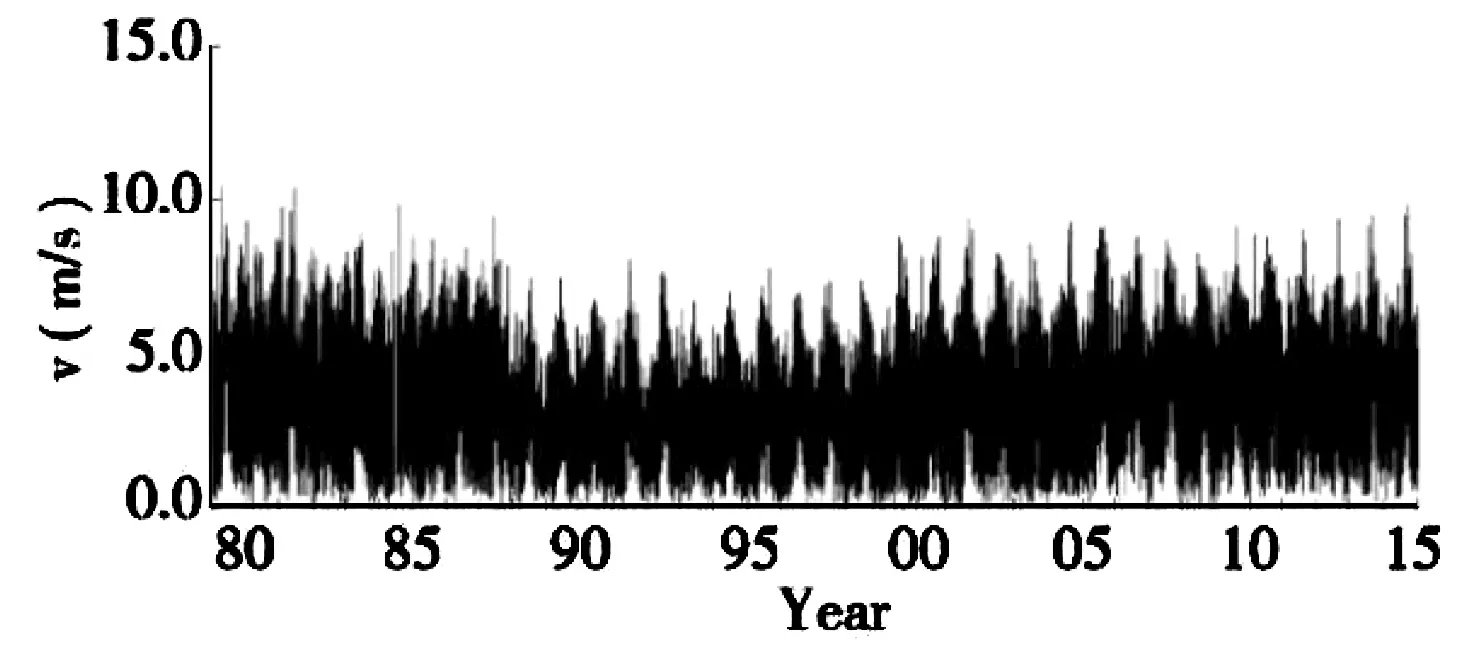
图4 马拉博外海GEW 站1979 年~2014 年风速的时间变化过程Fig.4 Diagram of wind speed variation over time at the GEW station in the open seas of Malabo from 1979 to 2014
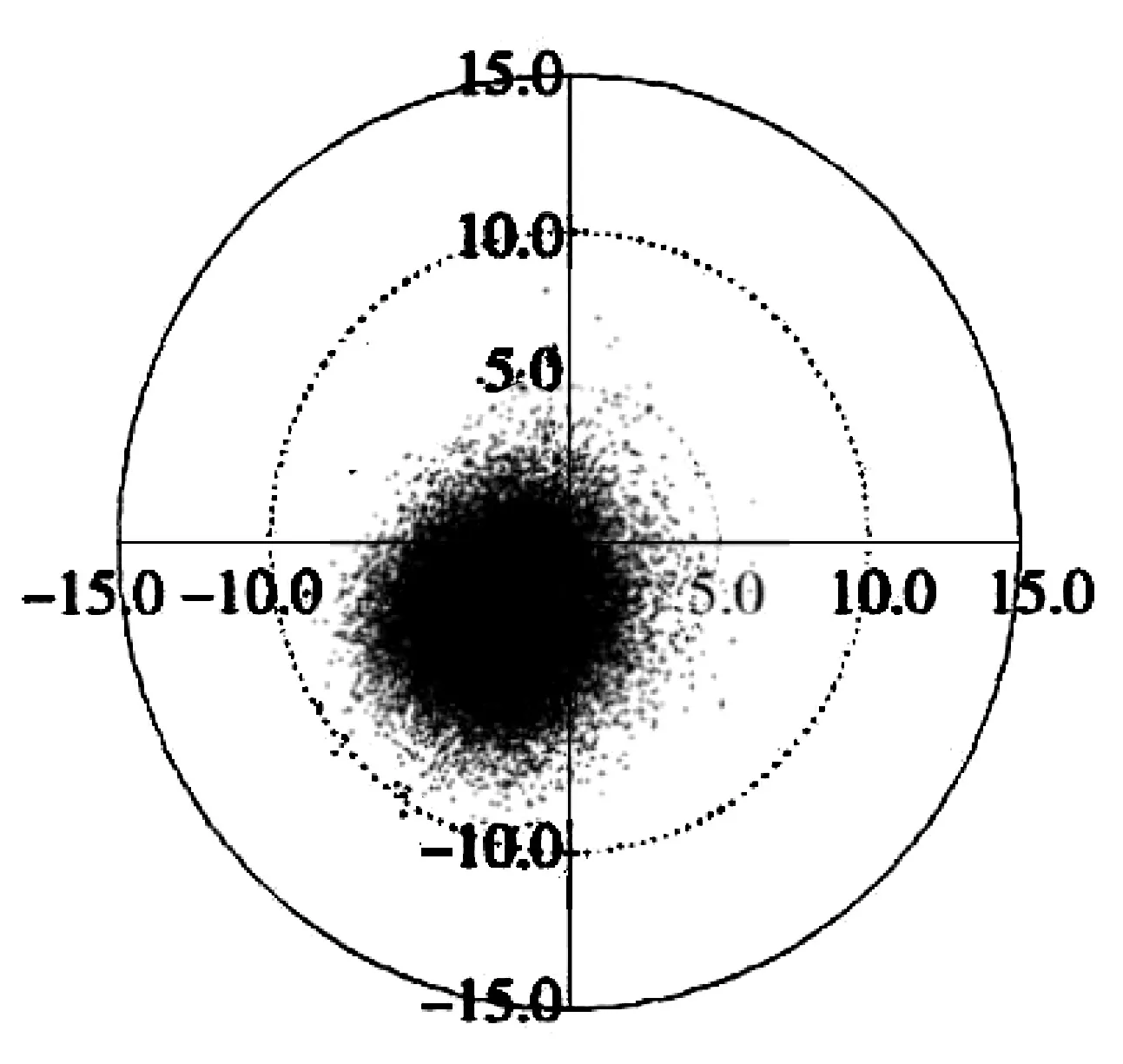
图5 马拉博外海GEW 站1979 年~2014 年风速(m/s)、风向(°)散点分布Fig.5 Scattered distribution of wind speed (m/s) and direction (°) at the GEW station in the open seas of Malabo from 1979 to 2014
2)风况
基于GEW 站1979 年~2014 年的数值风场资料,对马拉博外海平常年的风况进行了统计。图6所示为各向平均风速和频率玫瑰图,表2 给出了各向平均风速和最大风速的统计结果,图7 对不同方向、不同风级风的出现频率进行对比。上述图表结果显示,在马拉博外海。
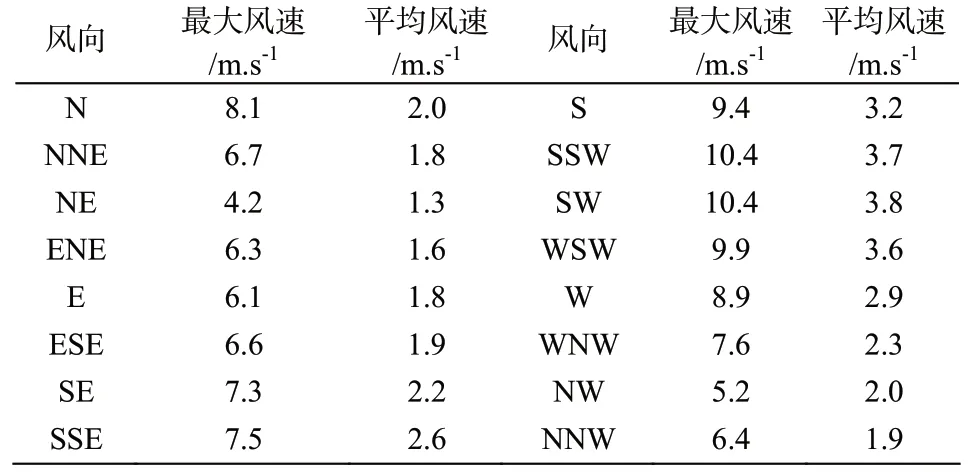
表2 马拉博外海GEW 站各向最大风速和平均风速(1979~2014)Tab.2 Maximum and average wind speeds in all directions at the GEW station in the open seas of Malabo (1979-2014)
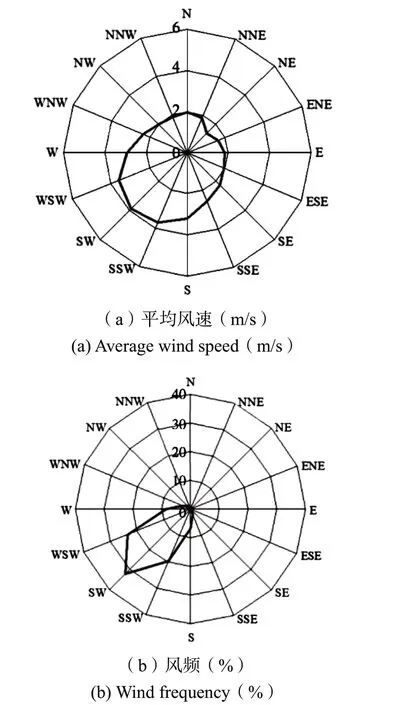
图6 据1979~2014年数值风场资料得到的马拉博外海GEW站风玫瑰图Fig.6 Rose diagram of wind of GEW station in the open seas of Malabo based on numerical wind field data from 1979 to 2014
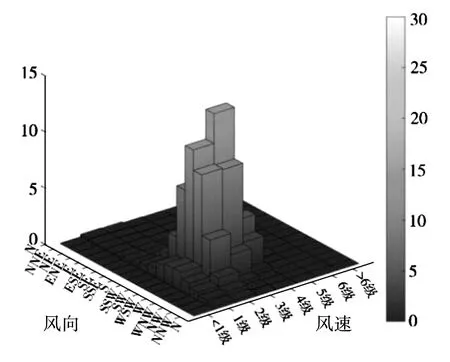
图7 马拉博外海GEW 站各向风速的分级统计结果(1979~2014)Fig.7 Classification statistical results of wind speed in all directions at the GEW station in the open seas of Malabo (1979-2014)
①出现频率较多的风向在S~W 向,此方位内的风频高达90.2 %,其中又以SW 向风频为最大,频率为31.7 %;NNW~SE 向风频率很低,频率仅为3.7 %。②各向风的强度以S~W 向为最大,多年平均风速在 2.9~3.8 m/s,多年最大风速在 8.9~ 10.4 m/s。4③级以下风出现的频率高达99.7 %;5级以上风的出现频率极低,仅为0.29 %,且主要集中在S~WSW 方位内。
3)重现期风速
曾参与入世谈判的龙永图,这样对比中国加入世贸组织前后的变化:过去只有一二百家能做进出口的企业,一下变成十几万、几十万家在做!中国入世后十年,每年进出口量以百分之二十、三十的速度增长,“这是历史上从来没有的!”
基于GEW 站1979 年~2014 年的数值风场资料,统计得到了该站各向的年极值风速,并据此采用PIII 型理论频率曲线[10],分析得到了不同方向和不同重现期的风速。考虑到数值风场数据为6 h 间隔,会造成峰值的丢失,极值风速偏小,为此报告使用“1.44”的校准系数,校正得到了马拉博外海不同重现期设计风速如表3 所列。结果显示,50 年一遇设计风速以SW 向为强,为15.2 m/s,2 年一遇设计风速SW 和SSW 向基本相当,为11.3 m/s。
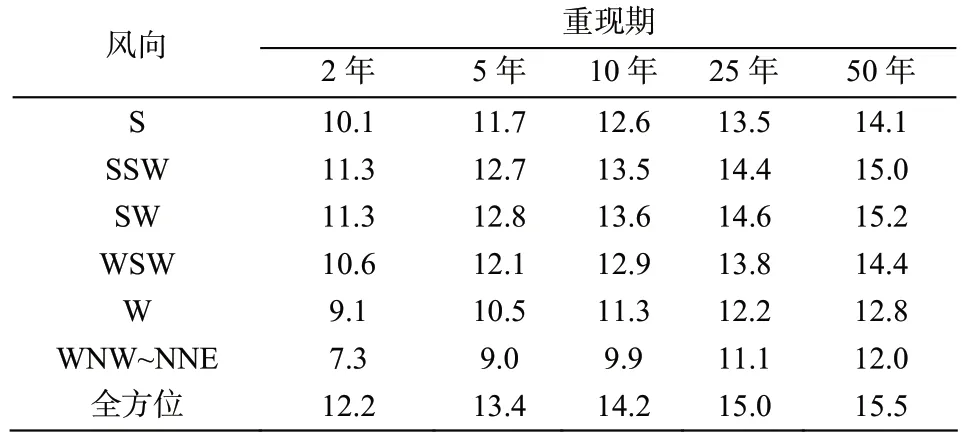
表3 马拉博外海GEW 站不同重现期设计风速(m/s)Tab.3 Design wind speeds (m/s) for different return periods at the GEW station in the open seas of Malabo
3.2 波浪
1)数据源
为分析马拉博外海不同重现期的波浪要素,基于HHU 南大西洋海浪数值后报结果,提取了GEW站(8.0 °E,3.75 °N)1979~2014 年共计36 年的连续波浪数据,图8 给出了该站有效波高VS 平均波向的散点分布。
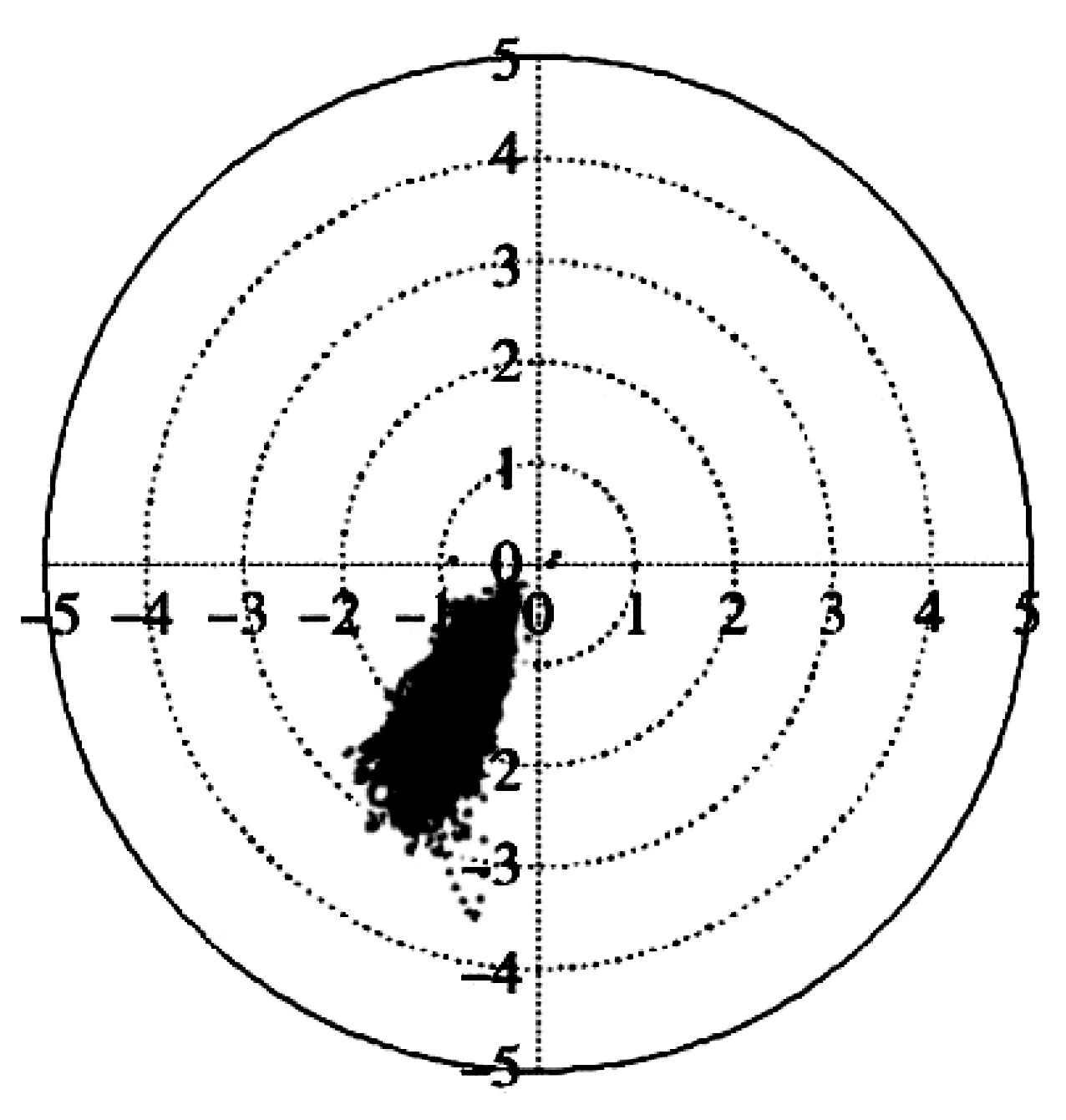
图8 马拉博外海GEW 站有效波高vs 平均波向的散点分布Fig.8 Scatter distribution of significant wave height vs average wave direction at the GEW station in the open seas of Malabo
2)波况
根据1979~2014 年HHU 南大西洋海浪数值后报结果,分别对马拉博外海GEW 站进行各向H13%波高的分级统计、波高VS 平均波周期的分级统计以及有效波高VS 谱峰波周期分级统计,图9 给出了H13%波高的分级统计结果,表4 对各向平均有效波高和年极值有效波高的平均值进行对比。上述结果显示,在马拉博外海:①盛行浪向为SSW~SW向,频率高达99.9 %,其中SSW 向频率略高于SW向,为54.1 %;1.5 m② 以上有效波高出现频率为25.9 %,2.5 m 以上有效波高频率为0.54 %,历年最大有效波高为3.52 m,对应的平均波周期为13.1 s,发生于SSW 向;6.0 s③以下平均波周期波浪的出现频率约为37.6 %,8.0 s 以上平均波周期的频率约为14.5 %;④对于有效波高大于2.5 m 的波浪而言,平均波周期出现在8.0 s~14.0 s,以10.0 s~11.0 s 出现频率为最高;⑤谱峰波周期的出现范围非常分散,对于有效波高大于2.5 m 的波浪而言,谱峰周期主要分布于12~19 s,其中,以15 s~16 s 为最大;⑥在各向波浪的强度上,SSW 向浪强于SW 向,年极值有效波高均值分别为2.56 m 和2.31 m,年极值有效波高最大值分别为3.52 m 和2.88 m。

表4 马拉博外海GEW 站各年极值H13%波高统计结果Tab.4 Extreme value of H13% wave height at the GEW station in the open seas of Malabo for each year
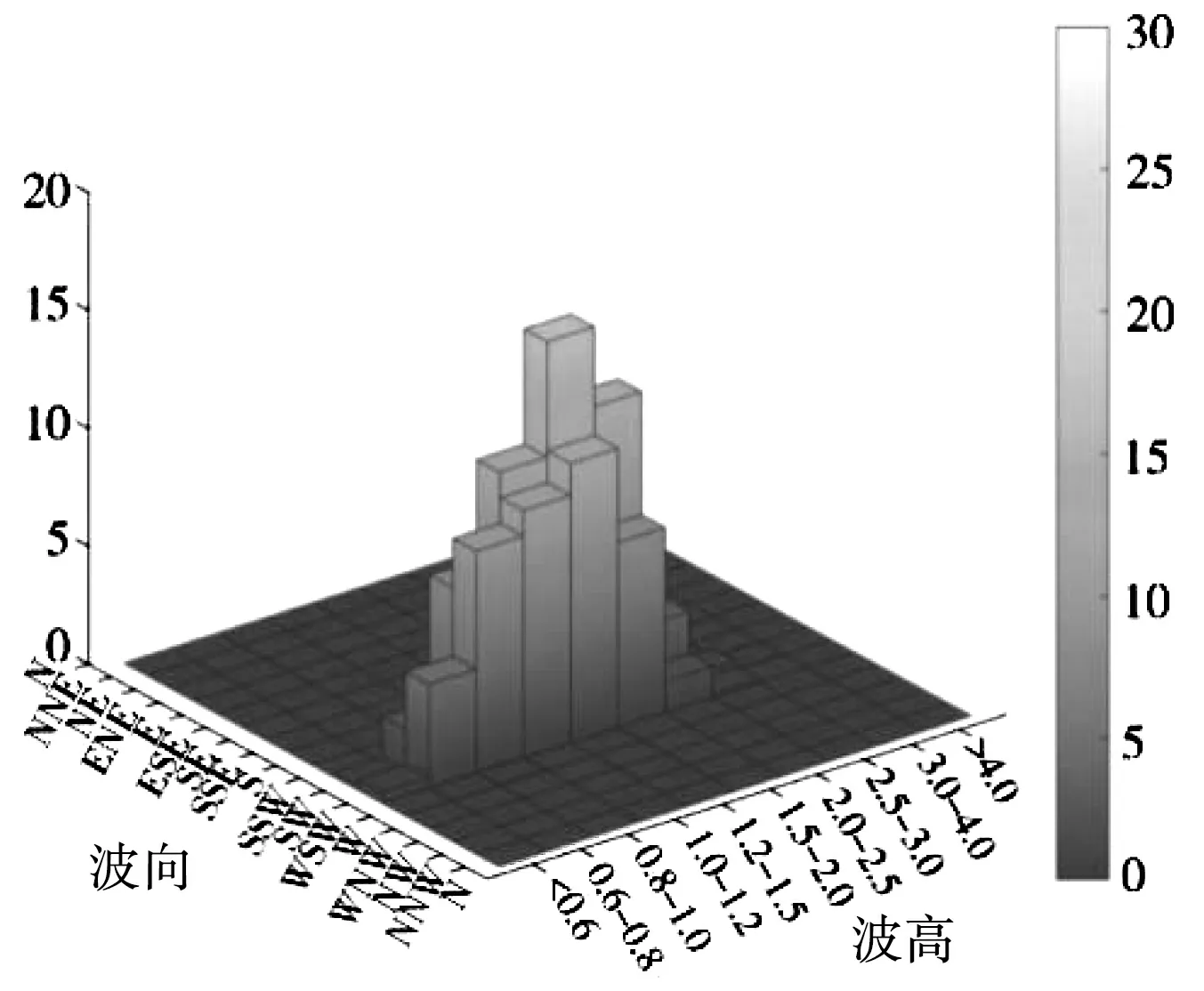
图9 马拉博外海GEW 站H13%波高分方向、分级频率统计结果Fig.9 Statistical results of H13% wave height at GEW station in the open seas of Malabo in different directions and frequencies
3)极值波浪要素
据1979 年~2014 年HHU 南大西洋波浪后报数据得到的、不同方向的年极值有效波高及其对应的平均波周期资料,采用PIII 型理论频率曲线,分析得到了马拉博外海GEW 站不同方向、不同重现期的有效波高和对应的平均波周期,如表5 所列。
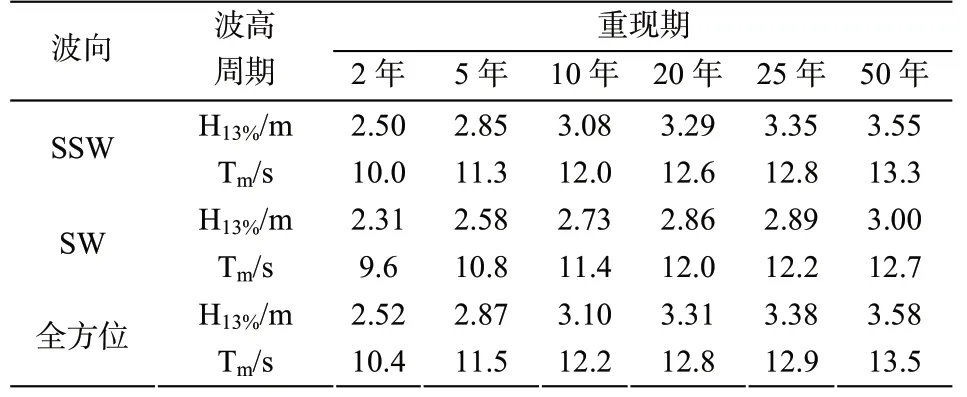
表5 马拉博外海GEW 站不同重现期H13%波高分析结果(1979 年~2014 年)Tab.5 Analysis results of H13% wave height at GEW station in the open seas of Malabo at different return periods (1979-2014)
上述分析结果显示,在马拉博外海GWE 站:
①SS W 向浪强于SW 向,此两方位50 年一遇的H13%波高分别为3.55 m 和3.00 m,对应的平均波周期分别为13.3 s 和12.7 s;2 年一遇波浪的H13%波高分别为2.50 m 和2.31 m,对应的平均波周期为10.0 s 和9.6 s;
②不分方向的50 年和2 年一遇的有效波高分别为3.58 m 和2.52 m,对应的平均波周期分别为10.4 s 和13.5 s。
4 结语
本文基于数值风场资料(包括“CCMP”和“CFSR”数值资料)、以及“HHU 南大西洋海浪数值后报数据集”(1979 年~2014 年),分析了赤道几内亚马拉博外海GEW 站的深水风浪条件,统计了马拉博外海的风况和波况,并给出了两站不同重现期的设计风速和设计波浪要素,为后续仅岸波浪的传播变形计算提供了深水波浪条件。相关分析结果显示:
风况:1)风向集中出现在S~W 向,风频高达90.2;2)各向风的强度以S~W 向为最大,多年平均风速在 2.9~3.8 m/s,多年最大风速在 8.9~ 10.4 m/s;3)4 级以下风出现的频率高达99.7 %;5级以上风的出现频率极低,仅为0.29 %,且主要集中在S~WSW 方位内;4)50 年一遇设计风速以SW向为强,为15.2 m/s,2 年一遇设计风速SW 和SSW向基本相当,为11.3 m/s。
波况:1)盛行浪向为SSW~SW 向,频率高达99.9 %;2)1.5 m 以上有效波高出现频率为25.9 %,2.5 m 以上有效波高频率为0.54 %,历年最大有效波高为3.52 m,对应的平均波周期为13.1 s,发生于SSW 向;3)从极值波浪条件上看,SSW 向浪强于SW 向,此两方位50 年一遇的H13%波高分别为3.55 m 和3.00 m,对应的平均波周期分别为13.3 s和12.7 s;2 年一遇波浪的H13%波高分别为2.50 m和2.31 m,对应的平均波周期为10.0 s 和9.6 s。
