钦州湾波流耦合作用泥沙输运特性研究

朱 峰，陈良志，覃 杰

（中交第四航务工程勘察设计院有限公司，广东广州 510230）

引言

三娘湾位于钦州湾外湾区域的咸淡水交汇区域，大风江和鹿耳环江等河流每年携带大量泥沙进入三娘湾[1]，同时由于三娘湾近岸区域底质多为淤泥，在涨落潮期间受到风浪扰动作用使得海水混浊度较高，特定区域存在一定的泥沙淤积风险[2]。

在充分考虑工程海域目前的海洋环境保护以及可持续发展需求的条件下，本文在对当地水深、水动力条件、泥沙现状详细排查的基础上，针对工程海域建立高分辨率水动力泥沙冲淤数值模型，开展局部区域冲淤变化分析，为工程海域的生态环境保护与可持续发展提供参考依据。

1 工程概况

三墩公路是一条长达13 km 的陆地—岛屿连接公路，该公路由人工填海形成。三墩公路是钦州湾临港工业发展与自然保护的伟大壮举，不仅是经济发展的底线、红线，也为保护北部湾生物多样性作出了巨大贡献。

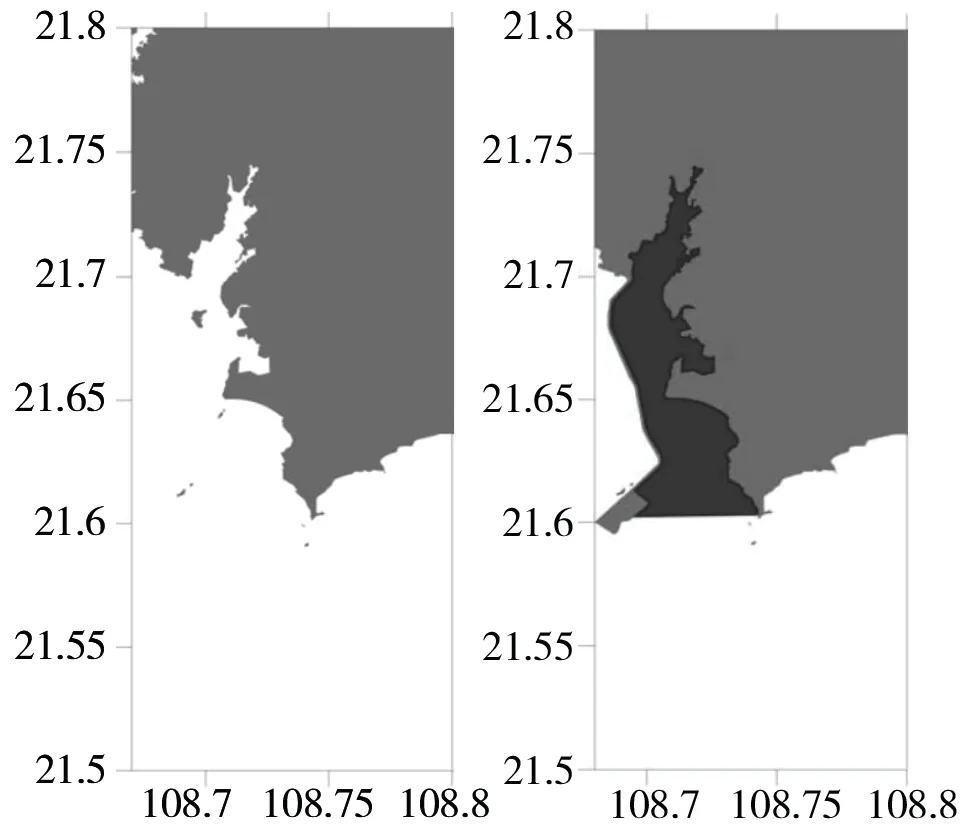
图1 三墩公路及东侧临港工业区Fig.1 Sandun road and the port eastern industrial zone

三墩公路东侧海域作为临港工业发展区，由于三墩公路的建设，其水体交换能力下降，导致其在工程形成后的数年内发生较为明显的淤积。因此需要对该片海域开展评估清淤2 m 后的水深条件是否能维持，纳潮量是否能有所增加。

2 泥沙输运模式

2.1 波流相互作用模型

为考虑波浪和海流之间的相互作用对底部切应力的影响，引入Grant-Madsen 模型[3]，采用迭代过程求解波流共同作用下的底部切应力。波浪引起的底摩擦切应力为：

其中：ρ 为水体密度；uw为波浪摩阻流速；fw为波浪摩擦系数；Uδ为近底波浪轨道速度。

通过迭代确定波浪引起的切应力增加系数：

1）假定波浪的切应力增加系数CRn=1.0；

2）计算CRn对应的波浪摩擦系数fw：

3）计算增大的波浪摩阻流速u*wm：

4）计算摩阻流速u*c：

其中：φcw为波浪与水流交角。

2.2 动力沉积模式

SED 模型是基于沉积动力学的物质输运数值模拟系统[4-5]，它包含了沉积物输运、沉积与再悬浮过程，可以计算分层悬浮泥沙浓度。其三维输运控制方程如下：

其中：k 为1、2，分别表示粘性泥沙（1-75 um）和非粘性泥沙（>75 um）；Ck为泥沙颗粒浓度，U、V 和W 分别为x、y 和z 方向上的水体流速。AH、KH分别是水平和垂直方向的涡扩散率，Ws,k为泥沙颗粒（絮团）沉降速度。

泥沙三维输运控制方程的边界条件为：在海表不考虑大气中的颗粒物，海底把泥沙沉降和再悬浮作为水体泥沙扩展的源和汇[6]。

其中：Ck为泥沙浓度，EK、DK分别为再悬浮和沉积通量。η 为自由表面，H 为水深。

对于粘性泥沙，再悬浮过程中的通量计算，采用如下公式[7]：

其中，ε 为再悬浮概率；a0为常数，与环境有关；Td为沉积时间，τb为底床剪切应力；τc为临界剪切应力；m、n 为环境参数。则输运方程中的粘性泥沙通量为[8]：

其中：fk为底床中粘性泥沙的百分含量。

沉降过程中粘性泥沙通量计算采用如下算法：

其中，D1为沉积通量，Ws,1为粘性泥沙絮凝沉降速率，C1为粘性泥沙浓度，P1为沉降概率。絮凝沉降速度由试验或者经验确定，沉降概率P1可以参考如下经验公式[9]：

3 模型计算与分析

3.1 模型设置

水动力计算网格模式如图2 所示。数值计算采用三维模式，计算网格的水平分辨率为100 m，垂直方向设置为均匀分布6 层。模型的南侧开边界由外海大尺度模型的计算或者观测结果插值得到。

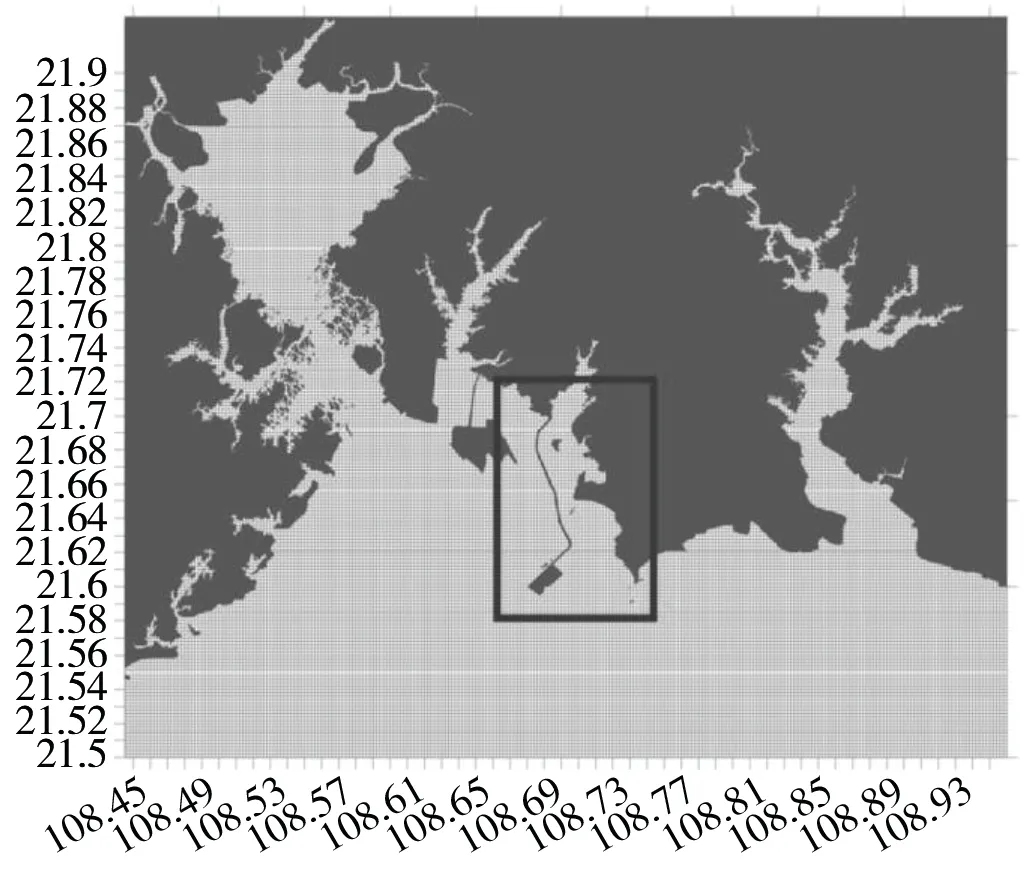
图2 模型计算网格Fig.2 Meshes for model calculation

计算区域的底摩擦系数最大取值0.0028，水平粘性和扩散系数由Smagorinsky 公式给出[10]。模型考虑了潮位变化引起的干湿边界变化，采用了干湿网格判别法对计算单元在每个计算步内进行更新。钦州湾的泥沙初始条件设置为45 mg/L，湾外开放边界处设置为10 mg/L。

3.2 潮流模拟验证

本文研究采用2013 年的潮流现场观测数据对计算结果进行分析验证。现场观测在三墩公路东侧布置有 ABCD 四个测点，测点的观测时间为2013/7/20～2013/8/20，如图3 所示。

图3 实际观测点位置分布Fig.3 Distribution of actual observation point

图4 列举了ABC 三个点上的观测结果与计算结果对比。图中列举了一个典型自然日内三个测点的水深平均流速与流向变化情况。在三个典型测点上，潮流的流速与流向的模拟结果与实测结果较为接近（注意水流方向0 °与360 °是指的同一个方向），计算结果与观测结果的相关度达到0.97。

图4 数值模型结果验证Fig.4 Verification of numerical model results

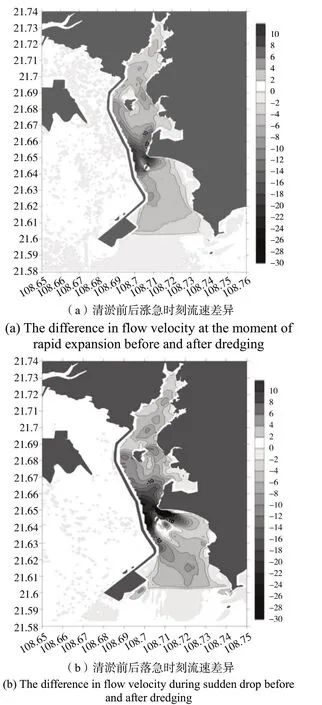
图5 清淤前后典型时刻流速差异Fig.5 Typical flow velocity difference before and after dredging

受限于篇幅，本文对波浪验证结果和泥沙验证结果不进行详细列举。因此关于模型的验证结果说明：计算模型与观测模型的吻合度较高，数值模型结果对实际工程的实施具有较高的技术指导价值。

3.3 工程区清淤后的结果评价

1）清淤前后流速变化

工程区域的流速变化是衡量清淤效果的重要参考指标，下图给出了三墩公路东侧清淤实施前后涨急和落急时刻的流速变化结果。计算结果显示：三墩公路东侧清淤完成后，整个片区在典型涨急工况下流速普遍减小，尤其是在位置相对较窄处，清淤后的流速比清淤前减小近30 cm/s，相对减小 35 %；在典型落急工况下，整个工程片区的流速依然以减小为主，仅在局部位置流速有所增加，但是流速的增加幅度不到10 cm/s，且位置主要集中在挡水建筑物附近的绕流区域。

2）清淤前后纳潮量变化

纳潮量是指一个海湾可以接纳的潮水的体积，纳潮量的大小反映海湾的自净能力，决定海湾与外海的交换强度，对海湾环境、生态及冲淤等方面意义重大。工程海域的纳潮量是三墩公路以东区域纳潮量。分析结果显示：清淤前三墩公路以东区域纳潮量为0.049105 亿m3，清淤工况实施后三墩公路以东区域纳潮量为0.049137 亿m3，增加了0.000032亿m3，增加幅度为0.065 %，由此可见清淤对工程海域的纳潮量影响较为有限。

3）清淤后回淤强度分析

工程海域清淤后，尽管纳潮量有微幅增加，但是由于流速整体有所降低，清淤之后整个工程海域面临着重新回淤的问题。因此定量评估工程海域的回淤速度是判断清淤深度是否合适的重要途径，同时也为后续的再次清淤疏浚计划提供定量参考依据。图6 给出了三墩公路东侧清淤后的年回淤厚度分布结果。

图6 清淤后的年回淤强度分布Fig.6 Distribution of annual siltation intensity after dredging

从图中可以看出：工程海域在清淤完成后，大部分区域呈淤积状态，平均回淤速度大致在每年2～4 cm，近岸区域的回淤速度较快，达到每年8～ 10 cm。工程海域的南侧区域由于局部流速有所增大，因此局部呈冲刷状态，冲刷速度大致为每年1～ 2 cm。

4 结语

本文以钦州湾三墩公路东侧海域清淤工程为原型，建立了平面二维数学模型开展波流耦合作用泥沙输运特性研究，在验证水动力条件计算结果与实际观测结果相符合的条件下，探讨了工程海域疏浚对水流特性分布、纳潮量变化以及工程后年回淤量的影响。

1）三墩公路东侧清淤完成后，工程海域流速普遍减小，典型涨急落急状态下，流速平均降低4～ 8 cm/s，局部口门较窄区域流速最大降低30 cm/s；

2）清淤后三墩公路以东区域纳潮量微幅增加0.065 %，由此可见，清淤完成后对该区域纳潮量增加贡献幅度有限，不会显著改变湾内的水体交换速率；

3）清淤完成后，由于流速降低，工程海域大部分区域呈淤积状态，平均回淤强度达到每年2～ 4 cm，近岸区域回淤强度较大，达到每年8～10 cm；海域南侧区域由于局部流速增大，呈冲刷状态，冲刷强度达到每年1～2 cm。整体而言，海域回淤强度较大，应进一步加强三墩公路以东区域的清淤与水土保持以满足生态环境要求。