考虑新能源出力不确定性的风-光-柴-储系统调度策略
2024-03-21张佳辉张洪福牛玉广王雨宸黄嘉鑫王孟桐
张佳辉,张洪福,牛玉广,王雨宸,黄嘉鑫,王孟桐
(1.国网北京市电力公司,北京 100031; 2.华北电力大学 控制与计算机工程学院,北京 102206)
0 引 言
在山区、海岛等一些电网接入难度较大的地区,风电、光伏等分布式能源(distributed energy resources, DER)凭借其经济可靠、安装简便等优点逐渐成为主要的供电手段。由多种分布式能源组成的微网系统,在经过合理的调度后,可进一步提升系统的能源利用效率[1-3]。
近年来,随着微网技术的逐步推广,如何经济、可靠地对微网调度已成为国内外学者研究的热点问题[4-5]。微网调度方式种类很多,但多数调度策略均可转化为多约束条件的非线性规划问题。例如,文献[6]对柴油机的出力特性曲线进行了深入的分析,并对曲线进行线性化处理,提出一种多时间尺度的微网调度策略。虽然该策略可以进一步提升系统的安全性和经济性,但并未考虑新能源出力不确定性对系统的影响。文献[7-10]考虑了新能源出力不确定性对系统的影响,但是忽略了负荷波动性的影响。文献[11]分析了蓄电池的出力特性,进而确定了微网的最佳运行方式。然而该策略仅仅考虑了系统的经济性,并未充分考虑系统的安全性和环保性。文献[12-14]在考虑新能源出力不确定性的基础之上,采用鲁棒优化控制对微网系统进行调度,使得系统的安全性大大提升。但此种方法需要付出较多的经济成本。文献[15]在考虑风电和光伏出力的不确定性的基础之上,提出风-光-柴-火多能互补随机优化调度的模型,并采用混合整数规划算法对模型进行求解,然而该方法求解过程过于复杂。
针对以上调度策略存在的问题,构建了风-光-柴-储系统,为了更好地描述新能源出力不确定性对系统的影响,提出了一种新能源出力复合预测模型。在综合考虑系统的经济性、安全性和环保性的基础之上,建立了考虑新能源出力不确定性的风-光-柴-储系统调度模型,并采用带有Monte Carlo模拟的遗传算法对模型进行求解。仿真结果表明,该调度策略可以有效平衡系统的经济性、环保性和安全性。同时,文章分析了系统负荷缺失率和置信概率概率对系统调度的影响。将所提出来的调度策略与其他调度策略进行对比,验证了所提出调度策略的优越性。
1 风-光-柴-储系统模型
1.1 系统结构
所研究的风-光-柴-储独立微网系统的结构如图1所示。系统的电负荷主要由风力发电机、光伏阵列、柴油机和蓄电池进行供给。此外,风力发电机、光伏阵列、柴油机可以将多余的电量储存于蓄电池之中。
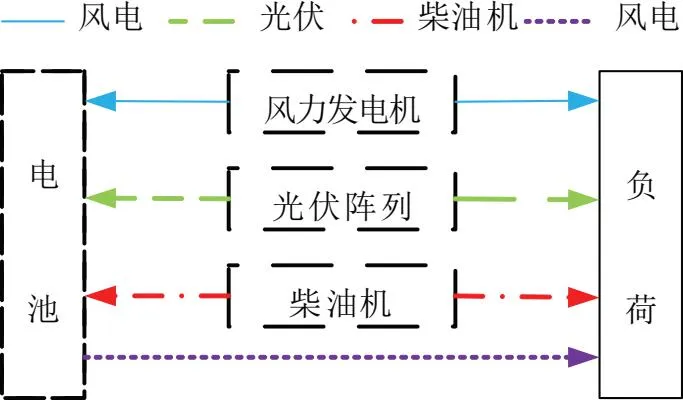
图1 风-光-柴-储系统结构示意图
1.2 柴油机模型
柴油机可靠性高且安装方便,其输出功率和所使用燃料量的关系如下:
Pdg(t)=αdg×Vdg(t)
(1)
式中Pdg(t)为t时刻柴油机的输出功率,kW;αdg为柴油机的燃料系数,kW/L;Vdg(t)为t时刻柴油机消耗的燃料量,L。
1.3 蓄电池模型
蓄电池有着“削峰填谷”的作用,同时还能提高新能源利用率,所采用的蓄电池模型如下:
(2)
Pc,min≤Pc(t)≤Pc,max
(3)
Pd,min≤Pd(t)≤Pd,max
(4)
SOEmin≤SOE(t)≤SOEmax
(5)
式中SOE(t)为t时刻蓄电池的剩余能量,kW·h;Pc(t)和Pd(t)分别为蓄电池t时刻的充放电功率,kW;SOE(t+1) 为t+1时刻蓄电池的剩余能量,kW·h;ηc为蓄电池的充电效率,即蓄电池内电量的变化量与充电量的比值:ηd为蓄电池放电效率,即放电量与蓄电池内电量的变化量的比值;βbat为蓄电池的自放电比例;Pc,min和Pc,max为蓄电池的最小和最大充电功率,kW;Pd,min和Pd,max为蓄电池的最小和最大放电功率,kW ;SOEmin和SOEmax为蓄电池容量的上下限,kW·h。
2 新能源出力复合预测模型
2.1 自回归滑动平均模型
自回归滑动平均模型(autoregressive moving average model, ARMA)是研究时间序列的重要方法,AMRA模型主要记录了系统过去一段时间内的自身状态和系统噪声。相比于AR模型和MA模型ARMA模型有更加精确的预测能力。ARMA模型的计算公式如下:
(6)
式中X(t)为t时刻的系统的状态值;ε(t)为t时刻的系统的噪声;m和n为模型的阶次,采用AIC准则进行求解;φi和ξj为模型的参数,可采用最小二乘法等方法进行求解。
采用ARMA(3,2)模型对风电功率进行预测,采用ARMA(4,5)阶数模型对光伏阵列功率进行预测。
2.2 最小二乘支持向量机
最小二乘支持向量机(least square support vector machine,LSSVM)是支持向量机的特殊形式,该方法将支持向量机中的不等式约束转化为等式约束,大大降低了计算量,缩短了建模时间,其原理如下:
设训练样本集为T={(xi,yi),xi∈Rp,yi∈Rp,i=1,2…n},经过非线性映射φ(x)将样本映射到高维空间,在新样本空间中构造如式(7)所示的决策函数。
f(x)=ωT×φ(x)+b
(7)
式中ω和b为参数,可以通过结构风险最小化原则确定,其过程如下:
(8)
s.t.yi=ωT×φ(x)+b+ei,i=1,2…n
(9)
式中C为正则化参数;ei为误差变量。
利用拉格朗日乘数法将式(8)和式(9)转化为:
(10)
式中αi为拉格朗日乘子。
根据KKT条件可求得:
(11)
定义核函数K(xi,yi)=φ(xi)·φ(yi),将式(11)带入式(7)并进行消元,求得决策函数为:
(12)
采用风速、风向、温度和湿度作为LSSVM模型的输入来对系统的风电功率进行预测;选取光照强度、温度和湿度作为光伏功率预测的输入;采用径向基函数作为LSSVM模型的核函数;采用遗传算法对LSSVM模型中的正则化参数C和径向基参数σR进行寻优。
2.3 BP神经网络
BP网络(back-propagation network)又称反向传播神经网络。该方法通过对样本数据的训练,不断地修正网络权值和阈值,使模型输出不断逼近期望输出。所采用的BP网络结构如图2所示。
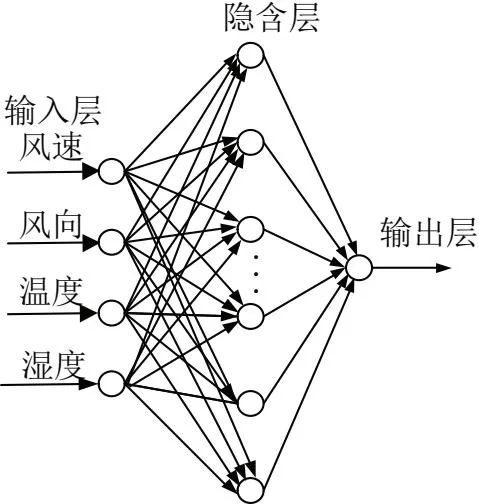
图2 BP神经网络预测风电出力结构图
选取风速、风向、温度和湿度作为风电功率预测BP网络模型的输入,隐含层层数为1,隐含层节点数为13;选取光照强度、温度和湿度作为光伏预测功率BP网络模型的输入,隐含层数为1,隐含节点数为11;传递函数均为Sigmoid函数。
2.4 复合预测模型
对任何一种预测方法,都有其优点和缺点。ARMA对短期的新能源出力预测较为准确,中长期预测误差较大;LSSVM和BP神经网络计算量大,对调参要求较高。为了将各种方法的优点进行融合,本文提出了一种复合预测模型,该模型的原理如下:
1)采用均方根误差来对每种预测方法的优劣程度进行评价,其计算公式如下:
(13)
式中ye(i)为模型的预测输出;y(i)为新能源出力的实际值。
根据式(13)计算得到三种预测方法前一日的均方根误差σRMSE-ARMA、σRMSE-LSSVM、σRMSE-BP。
2)分别采用三种方法对第二天全天24 h的新能源出力进行预测。
3)采用轮盘赌的方法对第二天每一时间段的新能源出力进行预测,每一种方法在每一时间段内采用的概率为:
(14)
式中pi为每种方法采用的概率。
大量统计数据表明,新能源的预测误差服从正态分布。假设采用复合预测模型的误差为服从均值为0,标准差为σ的正态分布,其中风电功率预测标准差为0.15×风电预测值、光伏预测功率标准差为0.1×光伏预测值。
3 考虑新能源出力不确定性的风-光-柴-储系统调度模型
在微网调度的过程中,主要考虑系统的经济性、环保性和安全性。综合考虑了微网系统的这三种特性,并考虑了新能源出力不确定性对系统调度的影响,构建了如下风-光-柴-储系统调度模型。
3.1 目标函数
为使风-光-柴-储系统更加经济、环保和安全地运行,以系统一个调度周期内的燃料费用f1、设备维护费用f2和污染物处理费用f3为目标函数,即:
minf=f1+f2+f3
(15)
(16)
(17)
(18)
式中cfuel为燃料费用,元;cdg、cwt、cpv和cbat为柴油机、风力发电机、光伏阵列和蓄电池的维护费用,元/kW;Pdg(t)、Pwt(t)、Ppv(t)和Pbat(t)为t时刻柴油机、风力发电机、光伏阵列和蓄电池的输出功率,kW;γNOx、γSOx和γCO2为污染物排放因子,g/L;cNOx、cSOx和cCO2为污染物处理费用元/g。
3.2 约束条件
3.2.1 功率平衡约束
为了描述系统的安全性,以系统的负荷缺失率(load loss rate, LLR)和置信概率α为指标,其中负荷缺失率的计算公式如下:
(19)
式中Eloss为系统允许的最大负荷缺失量,kW;Etot为系统的总负荷,kW。
在考虑系统LLR和置信概率α的基础之上,系统的功率平衡约束为:
(20)
式中 Pr{·}为风电预测功率和光伏预测功率的分布概率描述。
3.2.2 风力发电机出力约束
0≤Pwt(t)≤Ppwt(t)
(21)
式中Ppwt(t)为风电的预测功率,kW。
3.2.3 光伏阵列出力约束
0≤Ppv(t)≤Pppv(t)
(22)
式中Pppv(t) 为光伏的预测功率,kW。
3.2.4 柴油机出力约束
Pdg,min≤Pdg(t)≤Pdg,max
(23)
式中Pdg, min和Pdg, max为柴油机的最小和最大出力,kW。
3.3 基于Monte Carlo模拟的遗传算法
建立的风-光-柴-储系统调度模型中的目标函数和约束条件多为线性,无需特别处理。式(20)为机会约束,采用带有Monte Carlo模拟的遗传算法对调度模型进行求解[16],求解过程如下:
1)输入参数,主要包括种群大小、交叉概率Pc、变异概率Pd等;
2)产生初始种群,并采用复合预测模型和Monte Carlo模拟产生新能源预测曲线,并对每个个体进行检验。如果有个体不满足条件,则重新产生,直到所有种群满足约束条件为止;
3)计算所有个体的适应度,并采用轮盘赌的方法进行选择;
4)对初始种群进行交叉和变异操作,并对得到的个体进行Monte Carlo模拟,如果交叉或者变异产生的个体不满足约束条件,则随机选取父代个体进行替代;
5)重复步骤3)和4),直到达到终止条件;
6)得到最优个体并结束求解。
使用遗传算法求解调度模型的流程图如图3所示。

图3 遗传算法求解调度模型的流程图
4 算例分析
4.1 数据准备
为验证所提出调度策略的优越性,构建了如下的风-光-柴-储系统,其中柴油机装机容量为3×100 kW、风力发电机装机容量为4×30 kW、光伏阵列的装机容量为60 kW、蓄电池的容量为300 kW·h、负荷缺失率为0.05、置信概率为0.99。采用三种方法对前一日的新能源出力进行预测的均方根误差如表1所示。遗传算法的参数如下:种群规模为20、交叉概率为0.6、变异概率为0.1,迭代次数为1 000。

表1 采用不同方法对新能源出力预测的RMSE
4.2 典型日分析
图4为一个调度周期内风-光-柴-储系统各机组出力分布,从图4中可以看出,在调度过程中,柴油机在整个调度过程中均为主要的供能方式。风电出力主要集中在下午15:00-18:00和夜间03:00—05:00、22:00—24:00,光伏出力集中在白天。蓄电池在04:00—05:00、23:00—24:00充电,在19:00—20:00、22:00放电,体现出了蓄电池“削峰填谷”的作用。

图4 风-光-柴-储系统各时段机组出力分布
4.3 不同负荷缺失率对调度结果的影响
为了研究不同负荷缺失率对调度结果的影响,文章分别将负荷缺失率设置为0.01、0.05、0.10、0.15和0.20 (置信概率为0.99),不同负荷缺失率下的调度结果如表2所示。从表2中可以看出,随着负荷缺失率的升高,系统的调度费用均有不同程度的降低,但此时系统经济性提升是以牺牲系统稳定性为代价。此外,从表2中可以看出,在置信概率较高的情况下,系统负荷缺失率对系统经济性的影响较小。在置信概率一定的情况下,通过调整负荷缺失率,可以在较小范围内对系统的经济性和安全性进行调节。

表2 不同负荷缺失率下调度结果
4.4 不同分位数对调度结果的影响
为了研究不同置信概率对调度结果的影响,文章分别将置信概率设置为0.99、0.95、0.90、0.85和0.80 (负荷缺失率为0.05),不同置信概率下的调度结果如表3所示。

表3 不同置信概率下调度结果
从表3中可以看出,随着置信概率的逐渐降低,系统的调度费用逐渐减少。相比于不同负荷缺失率所减少的调度费用,不同置信概率所减少的调度费用更多。这说明在平衡系统经济性和安全性的调度过程中,置信概率可以大幅度地进行调节。
4.5 不同优化方式的调度结果
为了验证所提出调度方法的优越性,文章选取了另外两种调度策略进行对比。其中,方式1为常规调度方式,即不考虑新能源出力的不确定性,此时在调度过程中不再出现甩负荷的情况。方式2为采用鲁棒优化对风-光-柴储能系统进行调度,具体过程如下:当置信水平为β时,可以求得风电和光伏的置信区间为[u-zσ,u+zσ],其中u为风电或光伏的预测均值,σ为标准差,z可根据置信概率进行确定。为了确保系统运行的安全性,采用风电和光伏置信区间的下限对风-光-柴-储系统进行调度(β取0.95)[17]。方式3为所提出的调度方式,失负荷率为0.01,置信概率取0.95。3种调度方式的结果如表4所示。

表4 三种不同调度方式的调度结果
从表4可以看出,所提出的方式3相比于方式1和方式2有更好的经济性。和方式2相比,虽然系统的稳定性有所下降,但是系统的经济性提升10.37%。与方式1相比,提出的调度策略安全性更强,能进一步减小由于新能源出力不确定性对系统造成的影响。
4.6 蓄电池充放电功率对系统“弃风”和“弃光”的影响
在前面的算例中,为了排除蓄电池对调度结果的影响,蓄电池的容量和充放电功率均被设为较大值。为了进一步探究蓄电池充放电功率对调度结果的影响,研究了不同充放电功率对风-光-柴-储系统的弃风和弃光总量的影响,结果如图5所示(负荷缺失率为0.05,置信概率为0.95)。

图5 不同充放电功率对系统弃风和弃光总量的影响
从图5中可以看出,风-光-柴-储系统的弃风和弃光总量随着系统充放电功率的增加而减少,但是会存在最佳的充放电功率,当蓄电池的充放电功率超过此值时,系统的弃风和弃光总量将不再减少。因此在进行蓄电池充放电功率选择时,要避免选择充放电功率过大的蓄电池,从而有效降低投资成本。
5 结束语
为了研究新能源出力不确定性对微网系统调度的影响,提出了新能源出力负荷预测模型,并假设预测误差服从正态分布。在考虑系统经济性、环保性和安全性的基础之上,构建了风-光-柴-储系统调度模型,并采用带有Monte Carlo模拟的遗传算法对问题进行求解。为了衡量系统的安全性和降低新能源出力不确定性对系统调度的影响,文章以负荷缺失率和置信概率为评价指标。根据算例分析可知,本文所提出的调度策略,相对于其他调度策略而言有更好的经济性,并且可以有效地平衡系统的安全性和经济性。此外,所提出的调度方法也可以应用于微网系统规划。
