基于DWT-Informer的台区短期负荷预测

李甲祎,赵兵,刘宣,刘兴奇

(中国电力科学研究院有限公司, 北京 100192)

0 引 言

电力负荷预测是电力管理系统的重要组成部分。短期负荷预测是指对未来几小时一天至几天的电力负荷进行预测的任务,开展短期负荷预测不但能为电力系统的安全、经济运行提供保障,也是市场环境下编排调度计划、供电计划、交易计划的基础[1]。精确的短期负荷预测是实现电力系统安全经济运行的基础,为电力市场的实时运行提供了重要的依据,同时也是提高发电设备利用率和经济调度有效性的重要保证[2]。

现有的短期负荷预测方法基本可以分为基于传统数学统计方法的负荷预测方法和基于机器学习的负荷预测方法两大类。

基于传统数学统计学方法的负荷预测,如回归分析法、卡尔曼滤波法、负荷求导法、指数平滑法等。该类方法的优点为结构简单,运算及预测速度较快且拥有较好的可扩展性[3]。然而传统数学统计学方法依赖于统计学规律特征,面对非线性的、不稳定的数据时常常无法准确提取数据特征、学习统计规律,表现较差。这种问题在短期负荷数据预测任务中表现更为明显。为了进一步提升算法的特征提取和学习能力,基于机器学习的方法应运而生。

传统机器学习方法包括支持向量机(support vector machine,SVM)、随机森林等。近十年来,基于进化算法或群智能算法的机器学习模型也被用于负荷预测工作,例如文献[4]将基于加权灰色关联度选取的历史负荷数据输入支持向量机,并采取人工蚁群算法对参数进行优化,提出了一种基于加权灰色关联度和改进的支持向量机与人工蜂群算法(ABC-SVM)负荷预测模型。文献[5-6]对传统机器学习负荷预测模型进一步改进提高其预测精度。然而传统机器学习在面对短期负荷预测问题时,由于经典模型结构较为简单,因此在处理多维数据输入时具有较大局限性,同时传统机器学习方法在挖掘长期的复杂非线性时序数据时易丢失大量信息导致预测精度不佳。

在机器学习模型中,近十多年来基于神经网络的深度学习算法凭借其在预测准确率上的明显优势,在时序性短期电力负荷的预测中已经得到了广泛应用。国内外研究学者通过改进单一预测模型及应用混合模型进一步提升电力负荷预测精度。电力负荷数据可以被视作对特定物理量以特定频率进行采样后获得的等间隔时间序列。基于循环神经网络结构的长短时记忆网络(long short-term memory,LSTM)凭借其对时序信息的动态处理能力已经被广泛应用于时间序列预测任务中。文献[7]利用高质量大规模电力负荷数据和环境气象数据对LSTM网络进行训练,证实LSTM网络模型可以根据以往的负荷数据和环境气象数据,对电力负荷进行精确度较高的预测。文献[8]建立了基于Wide &Deep-LSTM的深度学习短期负荷预测模型,兼具数值型与类别型数据信息融合特性和时间序列表达特性。文献[9]提出了一种基于聚类经验模态分解的CNN-LSTM超短期负荷预测模型,通过K-means算法聚类得到时序特征更加突出的时间序列,利用CNN挖掘数据间的特征形成特征向量,将其输入到LSTM中进行负荷预测。文献[10-11]提出了基于GRU等其他深度学习负荷预测模型,在其基础上改进了特征提取模块,使负荷预测具有更高的准确性。

注意力(Attention)机制通过对输入特征赋予不同权重以突出重要特征的影响[12],在图像处理、自然语言处理等多领域均被证明有益于提高深度学习模型性能,近年来注意力机制也被引入负荷预测问题中。文献[13-15]提出了基于注意力机制混合模型的短期电力负荷预测方法,并进一步通过结合模态分解等方法充分提取负荷数据中的有效特征。

尽管RNN可以较好地提取负荷的时序特征,囿于计算特性,基于循环神经网络的网络的串行计算方式严重限制了其并行的能力[16],近年来,其他网络结构也进入讨论范畴。Transformer模型摒弃了传统循环神经网络,基于自注意力机制提取序列之间的关联性,相较于RNN类网络,Transformer在长期依赖性、信息传递效率等方面均具有优势。文献[17]在原模型基础上提出了一种改进后适用于时序数据预测的Transformer模型。文献[18]提出融合模型XGB-Transformer用于电力负荷预测。文献[19]提出了用于长序列时间序列预测的新型Transformer模型Informer,该模型采用概率注意机制同时嵌入相关的时间特征,使模型可以有效预测长序列。本文在电力变压器和用电负荷的时间序列数据集上对Informer进行了测试,其性能优于LSTM等传统模型。

综上所述,文中所提出的基于DWT-Informer的台区短期负荷预测模型,首先采用DWT将输入的电流数据进行高低频率分解重组,对电流数据降噪,提高预测精度,再通过结合Prophet模块的Informer模型对台区短期负荷进行预测。最终通过消融实验结果和与其他预测模型对比分析,结果表明该方法能有效提高预测精度。

1 模型基本理论

文中所提出的基于DWT-Informer的台区短期负荷预测模型,其输入为台区的电流数据、电压数据、历史有功功率数据,其预测对象为该台区的有功功率,具体步骤如下:

1)通过Prophet模型对时间信号进行处理,提取时序特征;

2)通过离散小波变换将电气特性进行信号分解,实现对信号的降噪处理;

3)使用Prophet处理后的时序分量代替原Informer模型对时间分量的处理,将经过降噪后的数据输入改进后的Informer模型进行预测。

1.1 Prophet模型原理介绍

Prophet通过拟合历史数据,将时间序列分解为多种不同特征的分量。目前Prophet不仅在负荷预测这一问题上凭借其简单高效得以广泛应用,在时间序列整体分解方向上也凭借其高解释性应用广泛。它可以将时间序列分解为趋势项、周期项或节假日项,其表达式为:

y(t)=g(t)+s(t)+h(t)+εt

(1)

式中g(t)表示趋势项,指时间序列在非周期上面的变化趋势,其类型分为linear线性变化、flat平稳变化、logistics逻辑回归变化。文中使用默认设置的linear变化,其表达式如下:

g(t)=(k+α(t)Tδ)×t+(m+α(t)Tγ)

(2)

(3)

其中,k为基本增长率;δ为增长率调整向量;m为偏移量参数;γ为突变点处的平滑处理偏移量;αj(t)为在第j个突变点的指示函数α(t)取值;sj为第j个突变点所在时刻。

s(t)为周期项,一般来说以周或者年为单位,Prophet采用傅里叶级数拟合不同周期的周期性趋势,其表达式如下:

(4)

其中,P为周期;αγ、bγ为平滑系数,服从正态分布;N为平滑系数的个数。h(t)为节假日项,表示时间序列中那些潜在的具有非固定周期的节假日对预测值造成的影响。εt表示剩余项,其数值反应模型未预测到的波动,可视作高斯白噪声。

1.2 DWT离散小波变换原理介绍

小波变换(wavelet transform,WT)是对信号进行时频分析的重要手段。其将傅里叶变换中无限长的三角函数基变换为人为选择的、有限长度的小波基,解决了短时傅里叶变化窗口大小无法调整的问题,成为对信号进行时频处理与进一步分析其特征的重要工具。其含义表达式如下:

(5)

其中,ψ(x)为小波基函数;a为伸缩参数,对基本小波函数作伸缩;b为尺度参数反映位移。

对于许多信号,低频成分相当重要,它常常蕴含着信号的特征,而高频成分则给出信号的细节或差别,但高频信号中同样存在较多白噪声,因此需要对高频分量进行进一步细分去噪。

前人研究表明,输入数据质量对于负荷预测准确性有着重要影响,因此对于电流数据质量有着较高要求。DWT可以将信号分解为不同尺度的子信号,与傅里叶变换相比,离散小波变换能够更好地表达数据蕴含的信息。用于对电流信号进行降噪处理,使输入的电流特性更加明确。文中使用的软硬阈值相结合的DWT降噪方法可被建模如下:

σ=(1/0.6745)×median|yd|

(6)

(7)

(8)

(9)

其中,ya为小波变换后低频信号;yd为小波变换后高频信号;y为小波降噪后的电流信号;λ为阈值。

1.3 ProbSparse Self-attention稀疏自注意力机制

自注意力机制的输入形式为(Query、Key、Value),而后进行缩放点积(scaled dot-product),即:

(10)

其中,Q∈RLQ×d,K∈RLK×d,V∈RLV×d。

第i个query的Attention系数的概率形式为:

(11)

由于稀疏自注意力呈长尾分布,即少数点积对主要注意有贡献,其他点积对可以相对忽略。使用KL散度度量对query的稀疏性进行度量,第i个query的稀疏性评价公式为:

(12)

第一项是qi对于所有key求最大值,第二项为它们的算术平均值,基于以上评价方法可以得到上述ProbSparse Self-attetion的公式。

2 基于DWT-Informer的预测模型

由于电力负荷影响因素复杂多样,负荷数据具有高随机性以及大波动性的特点,因此对输入数据进行有效的特征处理对于负荷趋势走向预测的准确性有重要影响,文中则从预测前数据降噪、模型内部编码层等对预测模型进行改进,提出基于DWT-Informer的预测模型。

2.1 模型整体流程

通过Prophet模型处理时序特征代替原有Informer对时间序列的编码可以更明显地提取时序特征,通过离散小波变换对电流信号进行降噪处理使输入的电流特性更加明确,进而提高Informer对负荷的预测精度,具体流程如图1所示。

图1 DWT-Informer模型流程图

2.2 输入数据处理模块

输入数据处理模块主要分为Prophet模型对时间信号进行先验处理模块及DWT对电气特性进行降噪处理模块。

Prophet先验处理模块在文中模型中,将时间信息分解为趋势项、节假日项、以1日、7日、1月为周期的不同周期项,并直接作为Embedding层的输入。在相同的时间分量输入维度下,加入Prophet先验处理模块不仅包括原有的时间周期信息,还包括了与负荷相关的趋势项以及节假日项等,在不增加Informer运算量的前提下提高了预测精度。

DWT降噪处理模块将电流信号分解为高频与低频信号分量,对于高频信号而言,文中选取软硬阈值折中的方法对高频信号进行筛选,取式(8)中a=0.8确定其阈值。文献[20]比较了不同小波函数对电力负荷的处理能力,从中得出结论对于负荷预测任务最准确的为db4小波函数,因而文中选用db4作为小波基函数。大于阈值分量确定为信号产生的有效信息进行保留,而小于阈值的确定为噪声产生直接舍弃,最后将信号重组后得到对原始电流信号进行降噪处理后的新电流信号。

2.3 负荷预测模块内部结构

Transformer模型整体框架由编码器-解码器(Encoder-Decoder)组成,通过编码层对输入序列进行特征编码,得到隐藏状态输出序列后再进行解码,进而得到预测值。基于Transformer模型,Informer通过稀疏自注意力机制降低了计算的复杂度,通过自注意力蒸馏减少了预测网络的参数数量,更适合对时序数据进行预测。

模型的输入数据为:

(13)

模型输出为预测的输出数据,即:

(14)

Encoder编码器用于提取时序序列数据输入的远期依赖性,首先输入数据进入Embedding层,分为三个部分即数据的Embedding,位置编码和基于Prophet特征提取的时间戳编码。

由于Encoder的特征映射存在冗余组合,因此利用distilling操作对具有主导特征的优势特征进行赋予更高权重,并在下一层生成自注意力机制的特征映射。从j到j+1层的distilling操作的过程如下:

(15)

其中,Conv1d表示时间序列的一维卷积操作,选择ELU作为激活函数。

解码器Decoder解码器使用文献[21]提出的标准decoder结构,其的输入向量如下:

(16)

最后通过全连接层获取最终输出,该解码器结构可一次性生成全部的预测序列以缩短解码时间,改进的Informer结构图如图2所示。

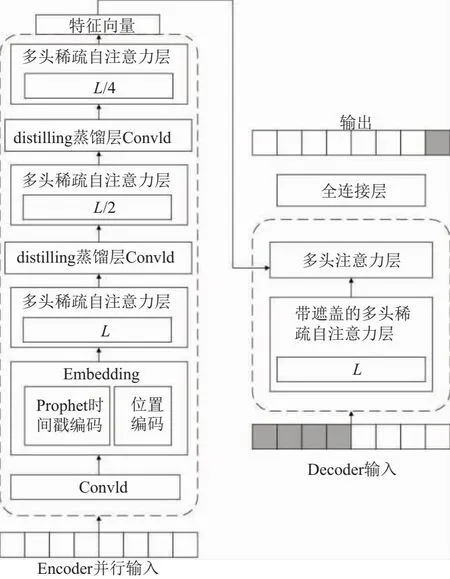
图2 改进的Informer结构图

3 实例结果

3.1 实验数据集及数据预处理

文中采用东南沿海某城市一台区2022年1月1日至2022年12月31日的电力负荷数据集(间隔15 min一个采样点,每日96点,包括电流数据、电压数据、无功功率数据、有功功率数据)共35 040组数据,数据集以6:2:2的比例划分为训练集、验证集和测试集。进行训练前采用min-max方法将原始数据进行归一化处理,计算公式如下:

(17)

其中,DWT-Informer主要参数如表1所示。

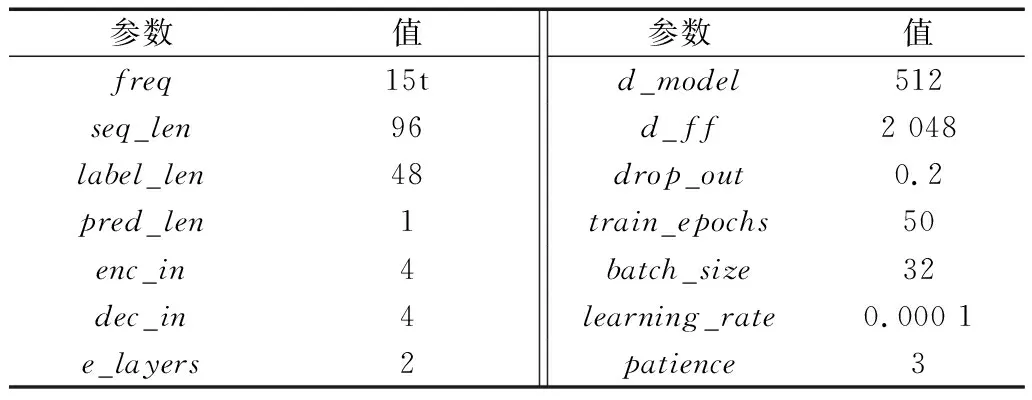
表1 DWT-Informer模型参数表

为了验证模型的预测精度,衡量指标使用平均绝对值误差(mean absulute error,MAE)、均方误差(mean square error,MSE)和绝对系数(R-square)。

(18)

(19)

(20)

3.2 特征提取及分析结果

通过Prophet对时间序列分解后的各组成部分如图3所示,其中趋势项通过linear变化可以看出,全年在2月、7月、8月该台区负荷趋势系数较高,其可能导致因素为:2月为春节所在月,7月、8月与夏天空调使用率高相关。负荷值一般与月周期、周周期、日周期相关,在傅里叶级数模拟周期性分量图中,其月、日周期特征相对比较明显,周周期特征并非十分显著,反映了每日该台区居民用户用电行为习惯为上午5时—12时、15时—21时,用电高峰为19时;每月中下旬用电量较低,月末及上旬用电量较高。通过自定义方式得到中国法定节假日列表,如图3所示其节日系数在春节、中秋节以及国庆节等节假日拥有较高的数值,反映了节假日特征对负荷影响显著。

图3 Prophet时序特征项

3.3 电气特性降噪处理结果

文中采用以db4作为基础小波、a=0.8的软硬阈值方法对原始电流数据进行分解重构,如图4所示。

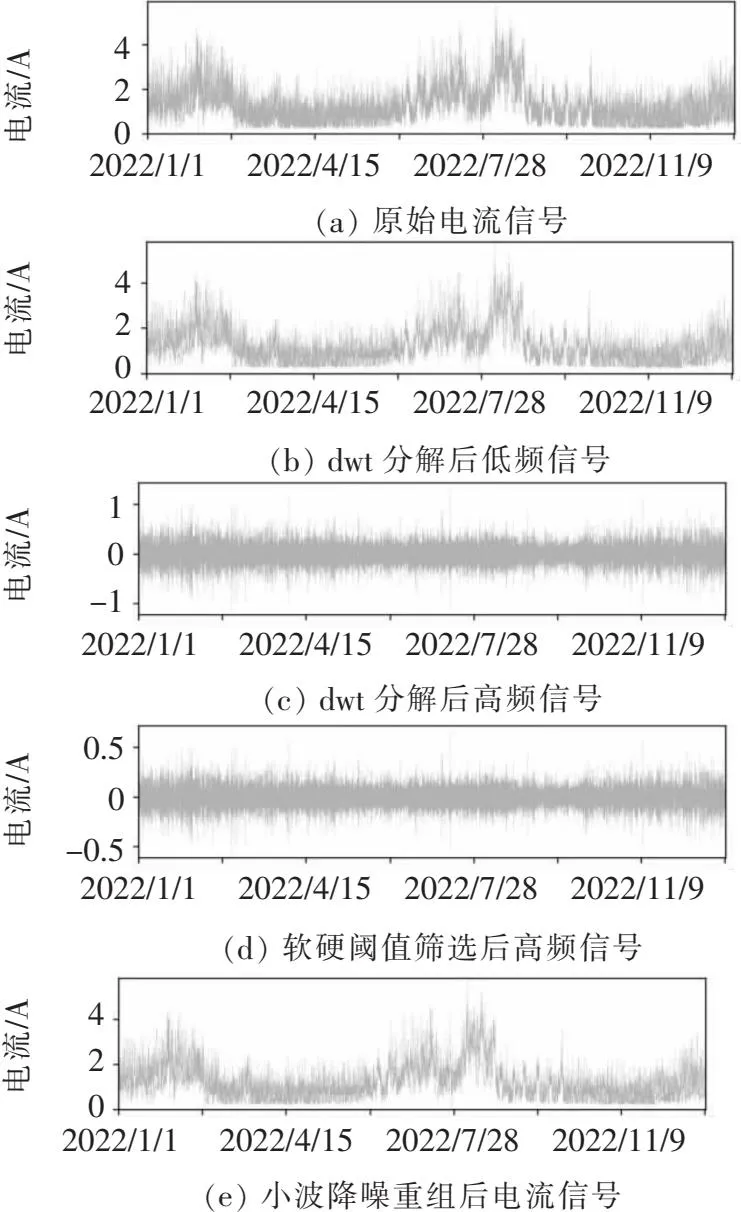
图4 DWT对电流信号分解重构结果

经软硬阈值筛选后的高频信号相较于初步分解后的高频信号,在保留其高频特征的基础上滤除了高频白噪声。如图经小波降噪重组后的电流信号相比原始电流信号,在保留其趋势特征的同时,高频噪声幅度明显下降。

3.4 DWT-Informer模型有效性验证

3.4.1 降噪处理模块有效性验证

为了验证DWT对电流信号降噪处理对于时序序列预测模型的有效性,对原始训练数据分别:不对电流信号进行处理、使用离散小波变换对电流信号进行处理,通过LSTM模型、GRU模型、Informer模型进行负荷预测,其结果如表2所示。

表2 DWT结合各模型性能表

从表2中可以看出,经过DWT对输入电流进行降噪后的预测效果均优于相对比的原始模型。其中,DWT-LSTM、DWT-GRU、DWT-Informer模型的MSE在预测任务的数值比相对应的基础模型分别降低了0.004 5、 0.004 5、 0.004 3;其MAE在预测任务的数值比相对应的基础模型分别降低了0.012 0、 0.012 6、 0.020 0;其R2在预测任务的数值比相对应的基础模型分别提高了0.089 2、 0.085 9、 0.084 8。

在各个衡量指标下,三个模型在输入经过DWT降噪后的电流数据预测结果均优于原始模型,说明输入电流数据的优质与否对预测模型的精度有重要影响,同时验证了DWT对电流信号降噪处理的有效性,即输入的电流数据经过DWT处理后在多种负荷预测模型上,都拥有更准确的预测结果。

3.4.2 Prophet模块有效性验证

为了验证Prophet对时间特征提取模块用于Informer的时间戳编码对于改进Informer预测模型的有效性,对原始训练数据分别采用:使用Informer自带时间模态分解模块、使用Prophet时间特征分解模块,在Informer模型对电流数据经过DWT降噪处理后进行负荷预测,其结果如表3所示。

表3 Informer模型型性能表

从表3中可以看出,使用Prophet提取后作为时间特征模块的输入其预测结果要优于Informer自带时间模态分解模块。模型的MSE在预测任务的数值降低了0.004 9;其MAE在预测任务的数值降低了0.022 1;其R2在预测任务的数值提高了0.094 7。

在各个衡量指标下,加入Prophet时间特征提取模块的改进Informer预测模型预测精度优于原Informer模型,验证了Prophet对时间处理用于Informer模型的有效性。

3.4.3 多种预测模型对比

为了探究文中方法的准确率提升,使用不同复合模型对相同的数据集进行预测,由于上文消融实验已证实DWT处理后在多种负荷预测模型上,均拥有更准确的预测结果,选择复合模型LSTM-D、GRU-D、XGBoost-D、TCN-D与文中所提出的复合模型做对比,其结果见表4。

表4 各复合模型预测结果与真实值比较

从表4中可以看出,相较于模型LSTM-D、GRU-D、XGBoost-D、TCN-D,DWT-Informer的MSE在预测任务的数值分别降低了0.001 9、0.001 3、0.003 1、0.000 9;其MAE在预测任务的数值分别降低了0.006 5、0.003 0、0.009 5、0.002 2;其R2在预测任务的数值分别提高了0.035 2、0.025 3、0.059 6、0.022 7。为了直观地观察各模型的准确率,选择测试集中的12月的两天共192个点,将其真实值与各模型预测结果相对比,其结果见图5。

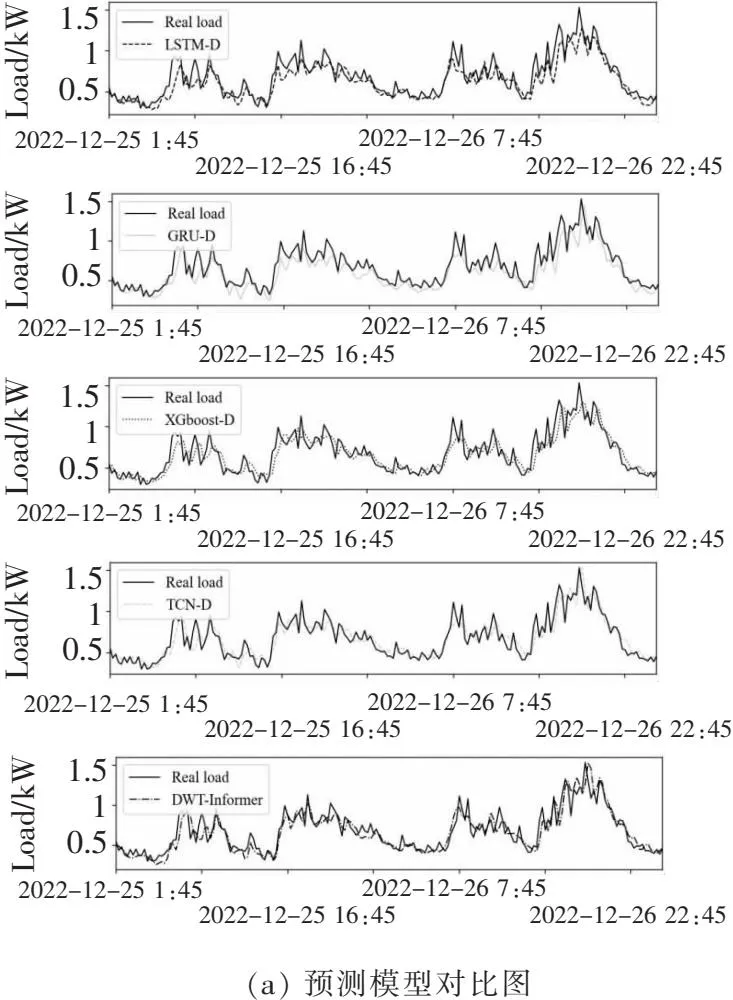
图5 不同预测模型对比

4 结束语

文中针对台区短期负荷预测问题提出了DWT-Informer网络模型,该方法综合考虑的电气特性与时间特性对预测精度的影响,通过DWT对输入的电流信号进行降噪处理,通过将Prophet分解应用于Informer使模型对时间分量的处理在相同的输入维度下,包含了更多与负荷功率相关的时间特征信息。通过实验验证得到了以下结论:

1)通过实验验证了LSTM模型、GRU模型、Informer模型与DWT结合均可提高预测精度,进而验证了DWT对电流信号降噪对于预测性能提高的有效性。

2)通过实验验证了将Prophet作为Informer的时间特征提取模块对于Informer预测性能提高的有效性。

3)通过将文中方法与其他经典模型的预测结果进行对比,得出DWT-Informer方法具有更优的预测性能,其MSE、MAE、R2分别为0.010 5、0.073 9、0.794 9。