基于分配因子和信息熵的母线负荷组合预测模型

2024-03-21李秀峰蒋燕高道春段睿钦刘梅燕鹏飞

电测与仪表 2024年3期

李秀峰,蒋燕,高道春,段睿钦,刘梅,燕鹏飞

(1. 云南电力调度控制中心, 昆明 650011; 2.北京清软创新科技股份有限公司,北京 100085; 3.华北电力大学,河北保定 071000)

0 引言

与传统的负荷总量预测不同,母线负荷预测更加关注电网调度的精益化水平,能够为地市一级的调度人员提供重要的参考。但是,区域变电站内的母线数量非常多,且电压等级不同,导致母线之间的负荷特性存在较大的差异,且存在较大的波动性和随意性,导致目前还没有一种特别有效的母线负荷预测方法,能够同时保证预测精度、稳定性,并且降低计算的规模与时间[1]。通常,母线负荷预测中,最为成熟的方法是基于数据外推的模型,如支持向量机[2]、神经网络模型[3]、机器学习[4]、组合预测模型[5]等,其中组合预测被认为是保障预测稳定性的重要方法。但是,由于母线特性的差异性,在实际操作时需要逐一单独预测,因此工作量很大,不利于实际工作的开展。另一类方法是基于负荷分配的方法,首先对系统总负荷进行预测,然后根据配比模型分配到每一母线上。此类方法的计算过程大大简化,但是对母线特性的考虑欠佳,分配因子如何确定较为困难[6]。如果能够构造一种基于两种方法各自优点的预测模型,则可以保证预测精度的同时降低工作量。文献[7-8]提出了一种虚拟母线技术的母线负荷预测方法,该方法体现了两种方法的结合,但构造虚拟母线较为复杂,且满足条件的电网情形并不多,不具有普适性。

本文采用组合预测模型在预测精度和稳定性上的优势,以及负荷分配方法在计算过程的精简性,提出一种全新的母线负荷预测方法。在预测过程中,历史数据的有效性是影响预测精度的一个重要方面。一方面,筛选与预测日情况(如温度、降雨、节假日等)较为相似的历史日,可以使历史数据的价值大大提升,文献[9]提出了一种基于数据新鲜度的预测模型,便是采用了这种思路;文献[10]依据关联度大小原则,运用相似日选择和长短期记忆的方法对历史负荷数据和气象数据进行排序,兼顾了负荷数据的时序性、周期性和非线性的特点,提高了预测精度。另一方面,筛选历史负荷数据也是确定组合预测模型权重的重要依据。除此之外,负荷分配因子也是影响预测精度的一个重要因素。文献[11]提出了基于负荷分配与最小二乘的母线负荷预测方法,但该模型中考虑了负荷的分配因素不够全面,导致的分配方法不够准确。实际上,母线负荷分配应该考虑区域性、电压等级、负荷特性等因素。文献[12]针对母线负荷特性各异,孤立性强的特点,针对各个母线节点,建立了立体化预测体系,通过构建不同属性的分配因子(包括电压等级能量流、拓扑结构负荷特性,能量流和拓扑结构相交构成的负荷基本预测单元),实现了电网任意节点母线负荷功率的有效预测。

立足于历史数据的有效性、组合预测权重的变化、以及负荷分配因子的确定方法,本文提出了一种基于分配因子和信息熵的变权重母线负荷组合预测模型。根据实际电网情况提出了负荷分配因子的概念及预测思路;充分考虑历史数据的有效性,在考虑日特征量和趋势相似度选取相似日的基础上,提出基于信息熵的变权重组合预测方法,提高类型负荷预测精度;结合类型负荷预测结果和负荷分配因子,最终得到各条母线的预测结果。

1 负荷分配因子的概念及预测思路

考虑如图1所示的电网结构,按照地区差异、电压等级差异、负荷特性差异等因素,可以将地区电网负荷细分为图1的结果。以城市电网为例,通常情况下,母线负荷即为变电站10 kV的出线侧所带全部负荷。考虑到负荷特性的相似性和差异性,可以将具有相同或相似负荷变化特性的母线负荷进行合并,称之为类型负荷。将实际电网进行抽象,可以得到图2所示的树形结构图。

图1 母线负荷分配示意图

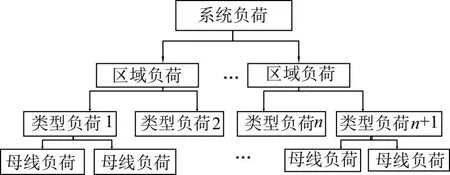
图2 母线负荷分配抽象图

在图2中,底层的母线负荷是最终需要得到的结果;具有相似特性的母线负荷可以进行聚类,得到类型负荷,聚类后的类型负荷值,可以有效地平抑各单一母线负荷变化的随机性,同时降低预测数量,提高计算效率。因此,本文预测的思路是根据地区特性对母线负荷进行细分和聚类,然后对各类型负荷进行预测;在预测结束后再以一定的分配方法得到各条母线的预测结果。这其中涉及到两个问题,类型负荷的预测方法及分配因子的确定方法。预测方法将在第2节进行详细叙述,下面介绍分配因子的计算模型。

假设前n天每小时的母线负荷为已知数据, 应用最小二乘模型对n天已知的历史数据进行分析,进而预测第n+1天各负荷的分配系数。

设PA,k,i(t)为类型k负荷在第i天、t时刻的功率值。采用y=p+q·i对前n天的负荷进行推算,由最小二乘法的相关公式,可得[13]:

(1)

(2)

式中k和t在每次计算中都是定值。

通过这种方式,能够较好地模拟n天负荷序列的变化情况。然后基于已知负荷序列,实现n+1天负荷值的预测。注意,这并不是最终准确的预测值。其计算方法为:

PA,k,i(t)=p+q(n+1)

(3)

考虑到母线负荷的周期规律性,对第i天的负荷值进行预测时,只提取前n天中具有相似特征规律的日类型数据,这样做的目的是简化计算和提高预测精度。所以需要进行相似日的选取,降低计算工作量和准确率。相似日的选取方法将在2.1节中进行说明。

通过改变t的取值,重复计算,可以得到n+1天内全天的负荷预测数据。此时,通过下式可以计算类型负荷分配系数KA,k,n+1(t)为:

(4)

式中C表示全部类型个数,c为计数变量。

2 母线负荷变权重组合预测模型

2.1 按日特征量和趋势相似度综合角度选择相似日

历史数据的有效性是影响预测精度的一个重要方面。一方面,筛选与预测日情况较为相似的相似日,从而使历史数据的价值大大提升;另一方面,筛选历史负荷数据也是确定分配因子和组合预测模型权重的重要依据。在很多相似日的选取方法中,均考虑了日特征量这一因素(如温度、降雨、日类型等),但缺乏对负荷变化趋势的考虑[14-15]。本文综合考虑了这两个因素选取了相似日。

定义日特征量:每日有H个相关因素,i,j两日的日特征向量分别为(ui1,ui2,…,uiH)T,(uj1,uj2,…,ujH)T。i,j两日的“特征相似度”为:

(5)

式中Oij表示日特征相似度,反映了这两日的特征量的几何空间距离。

然后计算趋势相似度:假设第i,j两日及它们前几日(设K日)的平均负荷序列分别为:

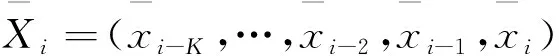
则i,j两日的“趋势相似度”为:

(6)

式中E代表均值,D代表方差。

需要说明的是,K的选取会对趋势相似度的结果产生一定的影响,通常情况下,对于短期负荷预测而言,负荷具有日相似度和周相似度,因此K的值不宜小于7;而如果K值选取过大,随着相隔时间尺度拉长,历史负荷数值对于未来预测的贡献度会逐渐降低,此时对于相似度的计算是不利的。因此,本文确定K值为7。

将Fij和Qij结合,得到:

Tij=μFij+λQij

(7)

λ+μ=1

(8)

式中μ、λ为适当参数,可以通过预测日和历史日已知的趋势相似度及日特征相似度,应用第1节中的最小二乘法求得。Tij越小,则i,j两日的时间序列越相似。

2.2 基于信息熵的变权重组合预测模型

(9)

(10)

文中提出一种基于信息熵的组合预测方法,它是表征预测效果和动态相似的结合。下面介绍基于信息熵的组合预测模型的权重计算方法。

1)目标属性的确定。

本文中的目标属性即为组合预测的预测精度,待求量为各单一模型的权重,将相似日序列各预测模型的预测值作为评估对象。

2)属性权重的计算。

信息熵计算各属性权重的具体步骤如下:

步骤1: 构造决策矩阵。构造预测时刻t下的决策矩阵et, 其中et为第i各模型在第j相似日的预测值。m为单一预测模型的个数,s为相似日的总天数。

步骤2: 求取特征值矩阵:

(11)

步骤3: 特征值矩阵规范化。对矩阵进行规范化处理,得到矩阵R。计算公式为:

(12)

步骤4: 矩阵R归一化。对矩阵R的每一行进行归一化处理,得到:

R′=(r′ij)m×n

(13)

式中:

(14)

步骤5: 计算属性信息熵:

(15)

考虑对数函数的性质,规定当r′ij=0时,r′ijlnr′ij=0。模型意义时某些时刻熵权特别小的模型其权重值可以为0。

步骤6: 计算权重向量:

(16)

更改t的数值,就可以得到一整天各个时刻的预测权重值。权重乘以预测结果,这样就得到了类型负荷的预测值et。最终各母线的负荷值应为各分配因子和预测值的乘积。

3 算例验证

以图1的电网为例,对全部母线负荷进行日负荷预测和连续一个月的负荷预测,以验证模型的精度和稳定性。将本文方法称为模型1,常规组合预测为模型2,SVM算法称为模型3。选取两类特性完全不同的母线负荷进行预测(采用归一化后的数值)。选取负荷特性迥异的两条母线作为展示特例,其中母线1为图1中的居民负荷,母线2为图1中的夜间工业负荷。

本文采用均方根误差RMSE、最大相对误差MPE表征预测模型的性能。RMSE能够较好地衡量模型预测的连续性和稳定性;而MPE能够较好地衡量预测模型失效的可能性。

(17)

(18)

选取该月中模型1的RMSE最大的一天作为展示,如图3所示。

从预测曲线图可以直观的发现,模型1的预测曲线更为平滑,且更加贴合真实负荷值。模型2和模型3的预测误差存在一定的波动性。表1给出了预测误差统计表。

从表1分析可知:

1)从负荷特性来看,由于负荷2的变化是更加规律的,因此在预测结果方面,尤其是RMSE,其预测误差明显更低;但是,模型3中对母线2的预测误差反而更高了,这说明单一预测模型很难在长时间尺度内维持良好的稳定性。

2)从RMSE来看,单一预测模型在某天的预测精度可能优于组合预测,这是因为组合预测的精度会受到各种单一模型表现的影响;但从预测指标MPE来看,组合预测(模型1和模型2)的预测稳定性要优于单一预测方法,模型3在某些时刻容易出现预测失效,误差高达0.3,突变增大的误差将造成系统震荡,这侧面证明了组合预测在稳定性上的优越性。

3)对比模型1和模型2,可以发现模型1的各项指标均优于模型2,这说明本文基于信息熵制定的权重计算方法,要比仅仅考虑预测误差最小化确定权重的方式更为科学合理。

4)从计算的复杂度分析,模型3计算需要57 min,而模型1仅需8 min。模型1的计算效率大大提高。

为了更加全面地说明预测结果,对该地区所有母线(共15条)进行负荷预测,统计相对误差的分布结果如图4、表2所示。

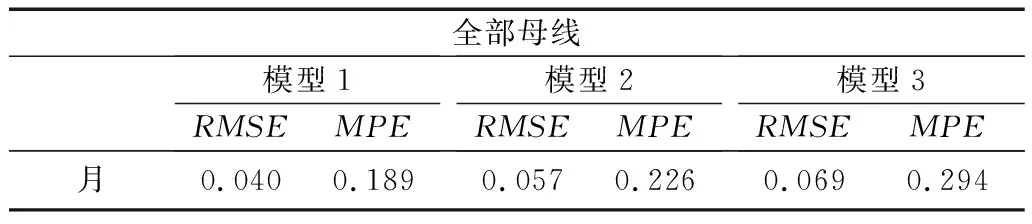
表2 全部母线误差结果统计

图4 误差分布曲线

统计所有母线的RMSE和MPE情况,并取算术平均值,作为最终整体的误差结果,如表2所示。

从所有母线负荷预测的统计结果来看,可以发现:

1)从误差分布的角度来看,模型1的误差分布更加靠近中心零点,呈现中间高,两侧低,曲线窄的规律分布,这说明本文的预测方法具有较高的稳定性,且预测精度较高;模型2和模型1的曲线形状类似,说明其预测稳定性也较好,但是曲线分布较宽,说明预测精度不如模型1;模型3的误差分布曲线较为不规律,最大误差偏大,预测稳定性较差。

2)从表格统计结果来看,三个模型RMSE和MPE的结果相较于一条母线结果偏高,这说明随着母线个数的增加,预测的误差也会有所增加,增加了模型失效的概率。