单极性ADC 静态参数的测试方法
2024-03-20韦凯陶青平
朱 清,韦凯,陶青平
(中国电子科技集团公司第五十八研究所,江苏 无锡 214035)
0 引言
随着MCU 和CPU 的发展,集成模数转换器的芯片越来越多,性能也越来越好,快速有效并且稳定地验证高性能片上模数转换器(Analog-to-Digital Converter,ADC)的性能变得尤为重要。INL 和DNL[1-2]作为模数转换器静态参数的重要指标,成为评价片上模数转换器性能好坏的关键。但是相比于单芯片ADC 测试,片上集成ADC 测试[3-4]的干扰因素变多,测试的环境更加复杂,对测试方法和测试设备的要求更加严苛。
传统的非线性参数测试根据输入信号是否为时间的函数主要分为静态测试和动态测试。静态测试主要有输入信号为斜波或者三角波的直方图测试法,以及改进后的伺服环积分法[5]。静态测试方法简单但是不能体现模数转换器在高频下的特性,动态测试方法通过输入一个高精度低非线性的正弦波信号,输出具有统计意义的样本进行分析,避免了额外的误差,解决了静态测试方法不能表征其实际高速性能的问题,被广泛用于测试高速数模转换器的非线性参数测试。但是动态测试方法对于输入信号的精度要求较高,使得激励的幅值和偏移的误差对测试结果的影响较大。对于系统级芯片(System on Chip,SoC)而言,测试环境较为复杂,测试激励的影响会更加突出。
基于此本文主要对片上单极性模数转换器的码密度直方图测试方法进行阐述,提出使用归一化的方法减小激励等误差带来的影响,使片上集成ADC 的测试更加稳定高效,并在SoC 芯片MSP430F169 上进行了验证,证实了方案的可行性。
1 码密度直方图法测试原理
码密度直方图法[6-8]是常用的静态参数性能测试方法,通过三角波或者正弦波作为测试激励,模数转换器对周期性信号进行采样。然而线性斜波输入改变得较为缓慢,所以被认为是静态测试,随着输入信号转换频率的逐渐增加,ADC 的动态非线性变得较差。将一个高频信号输入到ADC,较差的非线性将导致一个较大的谐波失真并且降低ADC 的性能。对于更高频率输入信号,正弦波比斜波更容易产生,且线性度更高,所以正弦波更加适合高频ADC 的测试[9-11]。然而用正弦波来评估ADC 会由于码的落点分布不均匀而增加计算的复杂度。另外码密度直方图法是利用统计学理论来进行测试,所以输入周期信号频率和采样频率互质可以保证采样的随机性,确保所有的采样点重合度最低。
对于单极性ADC 码密度计算方法如下。
正弦波电压Vin如式(1)、波形如图1 所示。
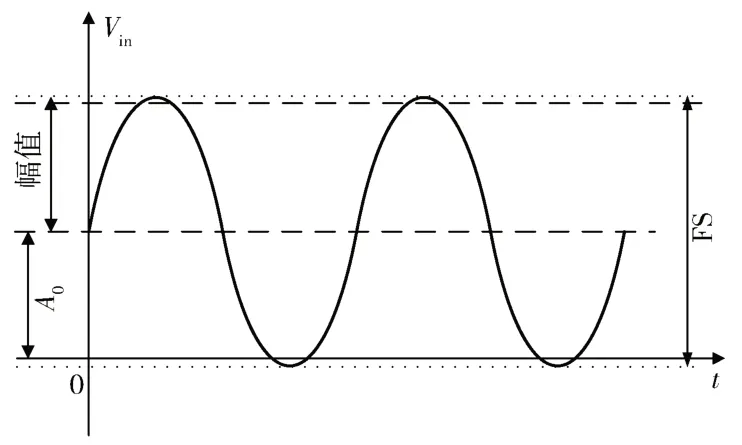
图1 正弦波输入波形
其中,Vin为输入的采样电压,A为正弦波幅值,A0为直流分量,FS 为满幅度量程。
由式(1)得:
在一个周期内:
△t为ΔV的时间间隔,ΔV电压出现概率为:
将式(4)代入(5)可得:
由式(6)对密度方程进行两点间的电压积分可以推出两点电压间的概率:
化简最后得到:
当V2和V1相差一个LSB 时,由p[V1,V2]可以推出p[n]:
由p[n]公式绘制出理想的码密度直方图如图2 所示。注意到越靠近正弦波的峰值概率越大,因为dv/dt最缓,而越接近中间值时dv/dt最大,也就是说每个码的落点越少。

图2 码密度概率曲线
一个正弦波的输入信号,第n个点的理论落点数量为:
第n个码相对应的DNL 误差:
用传统码密度直方图法要得到精确的结果必须至少考虑以下几个方面:(1)正弦波频率不可以是采样频率的次谐波;(2)正弦波的幅值必须比范围的两头要略微过驱;(3)通过调整正弦波的偏置来移除直流偏置;(4)正弦波的幅值需要进行精确的估算。
2 归一化幅值的方法计算INL 和DNL
直方图码密度统计法用于DNL 和INL 计算,其会受外部输入正弦波信号幅值[10]等因素的影响而较难预测,与测试平台的噪声和时间抖动也具有较大的关联,所以本文提出了一种归一化幅值的方法来更加稳定地评估DNL 和INL。
下面对单极性ADC 进行验证,正弦波输入ADC 进行一致性采样,偏移量为0,采样点数符合文献[6],计算方法如下。
输入信号正弦波极坐标曲线如图3 所示,由图3 得:
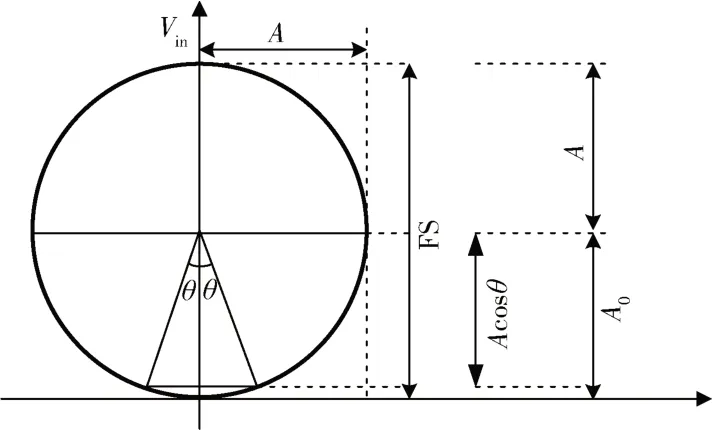
图3 输入信号正弦波极坐标曲线
其中,A为正弦波的幅值,Nt为总的采样点数,V(i)为第i个点的转换电压,CH(i)为在V(i)电压值以下的采样总数。
带有偏移电压的正弦波通过一致性采样,正的采样个数Np加上负的采样个数Nn等于总的采样个数Nt。带直流分量的正弦波极坐标曲线如图4 所示,由图4 得:
由式(14)和式(15)得:
由图4 可以计算出Voffset:
将式(16)代入到式(17)可得:
将计算得到的转换电压误差进行补偿,所以对应每个输出码的输入电平如下:
文献[6]、[8]已经给出了DUT 的LSB 测量方法以及DNL 的定义:
由式(20)和式(21)可知,符合幅值大小要求的正弦波幅值已经不影响DNL 的结果。下面通过实验来验证此方法的可行性。
3 测试平台方案和结果
本文提出的测试平台主要由测试激励、采集单元、控制单元、存储单元以及数据处理单元5 个部分组成,如图5 所示。测试原理为通过施加正弦波激励,经过低通滤波器滤波后由待测ADC 进行采集,数据经过控制单元缓冲后存储到外部SRAM 中,等待所有采样点数完毕后由数据传输单元将数据传送到PC 进行数据保存及分析。

图5 测试平台方案框图
正弦波激励的幅度须略大于ADC 的满量程幅值[10],在保证所有数字码都覆盖的条件下,尽可能让0 和2n-1 附近的码密度过渡斜率与标准码密度线接近。根据式(10)和式(11)所示,P[0]处和P[2n-1]处的码密度概率是最大的,在P[2n-1]处码密度概率最小,所以如果激励幅度过大导致0 码和2n-1 码箱数值增加过大,从而使其他码箱码密度过小影响测试精度。
本实验测试芯片为MSP430F169 芯片片上12 bit 高速模数转换器。MSP430F169 芯片集成了片内ADC 模块,对于这种类型的混合电路,测试单一性能指标受影响的因素较多,所以使用低通滤波电路对输入的信号进行滤波以减小电源抖动带来的噪声干扰。并且在测试片上ADC 时需要将其他功能模块失能,尽可能保证低的模块间耦合性,提高测试精度。
本实验采用200 kS/s 最高采样频率,1 kHz 低频正弦波作为测试激励,为了对所有电平不重复采样采用信号频率与采样频率互质,且测试点数满足:
将待测ADC 位数N=12,置信水平95%,误差精度β=0.1,Zα/2=2.58 带入式(22)求得总 采样点 数Nt≥2 471 680,取Nt=2 621 440。分别对传统码密度直方图法和归一化后的码密度测试方法进行实验。
传统码密度直方图法在GAIN ERROR 估算错误的条件下得到的DNL 和INL 如图6 所示。
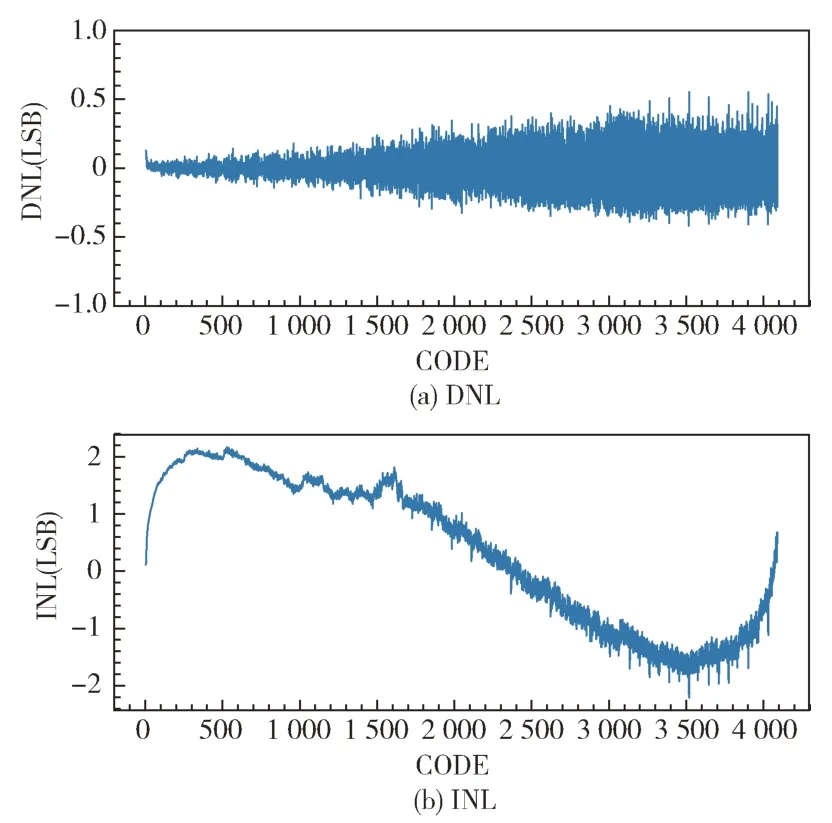
图6 GAIN ERROR 下模数转换器 DNL 和INL
传统码密度直方图法在OFFSET ERROR 估算错误的条件下得到的DNL 和INL 如图7 所示。
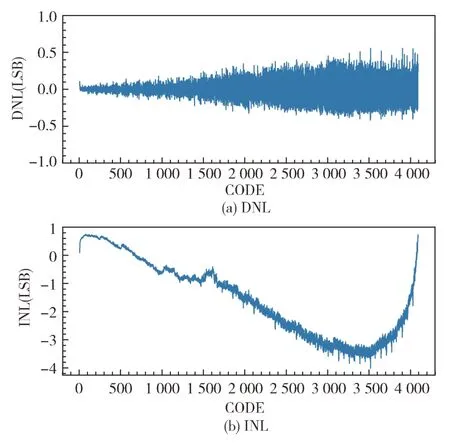
图7 OFFSET ERROR 下模数转换器 DNL 和INL
基于正弦波测试的码密度直方图法对于offset 和gain 的计算非常敏感,所以对offset 和gain 的正确估值对于码密度直方图法是非常重要的。
对于符合归一化方法幅值大小的选择,文献[10]中已经给出了判定方法,即所有的码密度落点几乎都在上下一个标准差内,说明测试激励的施加符合,本文选取误差精度为0.25 LSB 作为参数选择幅值的大小,计算DNL 和INL 如图8 所示。
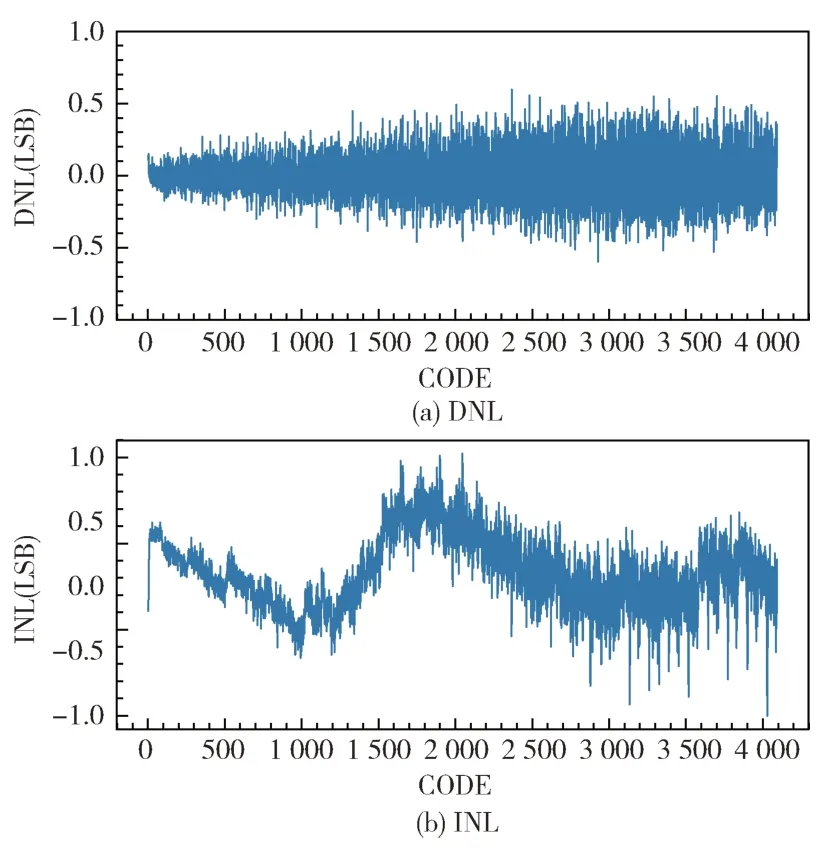
图8 3 V 范围的12 bit 模数转换器 DNL 和INL
为了评估不同测试幅度对于同一个芯片模数转换器的影响,常温(25℃)下选取3 个符合判定的不同幅值进行实验比较,每个幅值系数条件下测试20 次,如表1所示。
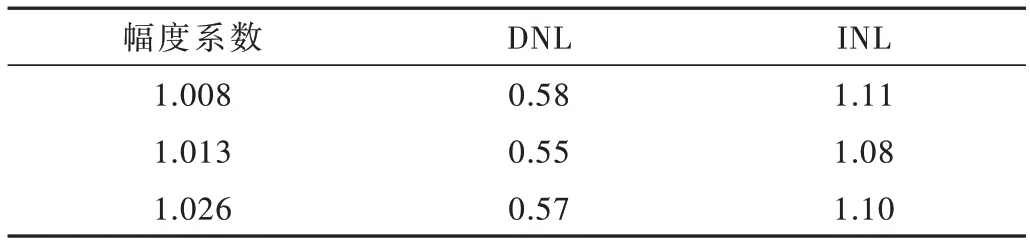
表1 不同幅值测试结果
经过上述实验,通过施加不同测试激励幅值,在获得足够样本的前提下得到的采样数据,经过归一化处理的直方图法能够较为稳定地衡量一个芯片的静态参数。
4 结论
码密度直方图法主要受样本总数和激励幅值的变化所影响,本文提出的归一化后的直方图法能够避免激励幅值的变化带来的不确定性,能够更加稳定地计算片上集成模数转换器的静态参数,更好地反映片上模数转换器的性能,并针对TI 的SoC 片上ADC 设计了测试平台,获得了稳定的测试结果。这种归一化的测试方法较易实现,可以实现ADC 快速、稳定和高效的测试。
