基于主轴电机电流信号的表面粗糙度检测*
2024-03-20刘雪杰李国富任潞
刘雪杰,李国富,任潞
(宁波大学 机械工程与力学学院,浙江 宁波 315211)
0 引言
表面粗糙度作为工件质量的重要评价指标,直接影响工件的耐磨性、抗腐蚀性、密封性、配合程度、传动精度[1],因此在工件工艺设计时都会优先考虑表面粗糙度。表面粗糙度的及时检测是十分必要的,当工件表面粗糙度不满足设计要求时需要及时调整工艺参数避免更大的损失。表面粗糙度的检测有多种方法,大致分为两类,第一类是采用接触式探针进行表面粗糙度检测;第二类是通过传感器采集图像、电流信号、振动信号或声发射信号进行分析处理,间接得到表面粗糙度值。接触式检测准确度很高,但是需要等待加工完成后才能进行检测,影响加工效率[2]。图像检测容易受到切削液和切屑的影响,另外图像检测需要高性能的工业摄像机,导致图像检测表面粗糙度价格昂贵。振动信号通常安装在刀具上,可能会干扰机床的加工,声发射信号容易受到其他机床的干扰[3],而电机电流信号是机床材料去除的动力来源,与加工过程十分密切,外界不易对机床电机电流信号造成干扰[4],并且主轴电流信号获取十分方便,距离较远也能轻松获取电流信号。使用电机电流信号进行表面粗糙度的检测研究比较少,主要原因是电流信号与表面粗糙度存在较为复杂的对应关系。
当前需要解决表面粗糙度不能及时准确检测的问题,采集的电机电流信号为正在加工时的信号,不必等到加工完成后才能进行检测,极大缩短了检测时间,使用电流信号检测表面粗糙度有天然的优势,但是电流信号蕴含的信息十分丰富,并不只有表面粗糙度信息,电机转速、主轴性能、刀具磨损等信息都混叠在电机电流信号上,需要充分挖掘电流信号。本文通过小波包分解对电流信号进行处理,将电机电流信号分解成不同频段,采用电流信号与表面粗糙度的互相关性筛选频段,留下的频段表面粗糙度信息占比较高,为了进一步降低特征的数量,采用随机森林算法评估特征的重要性,保留的电流信号特征维度较小,能够缩短检测的时间,重要性高的特征与表面粗糙度联系紧密,可解释性比较强。
1 主轴定子电流与表面粗糙度
1.1 主轴定子电流的数学模型
主轴定子电流为材料去除、传动机构正常运转提供能量,与主轴角速度变化有关。表面粗糙度通常指工件表面形貌的微小起伏变化,在车床加工中工件表面粗糙度受到多种因素的影响。工件材料的去除实际上是工件在刀具强烈的挤压作用下,材料发生剪切、滑移,材料从正在加工的区域剥离出来,不同的工件表面粗糙度摩擦系数不同,消耗的能量也不同,输出转矩与消耗转矩是一种动态平衡关系,所以不同工件表面粗糙度会对电流信号的波形重新塑形,还会对电流信号造成微小波动,可以从电机定子电流中提取到表面粗糙度信息。电机输出转矩与消耗转矩公式可以表示为[5]:
式中,k为电机转矩常数,I为交流电的等效电流值,Tm为电机输出转矩,J为传动机构的等效传动惯量,Tf为摩擦力矩,Tc为切削力矩。
车床切削为恒转速,主轴角加速度为零,传动机构是固定的不会发生变化,通常传动机构的摩擦转矩为一个稳态定值。电流信号的异常波动和表面粗糙度有关,表面粗糙度发生变化时,摩擦系数发生改变,导致电流信号随之发生变化。另外表面粗糙度是评价外表面形貌的凹凸不平参数,在加工过程中,切削量也会发生细小变化造成电流信号细微波动。正在加工时的电机电流信号如图1 所示,从整体上看原始电流信号为正弦信号,电流信号局部存在并不规整的小范围波动。

图1 原始电流信号
1.2 定子电流信号的小波包分解
虽然傅里叶级数拟合能够去除稳态电流信号[6],但是当信号点数多、电流信号频率存在波动时拟合的效果会变差。而电流信号的表面粗糙度成分提取的关键在于电流信号中奇异信号的检测,小波包能够对信号进行精细的划分,小波包分解有很强的时频分析能力。电流信号中的突变成分与表面粗糙度关系明显,需要强有力的时频分析工具,小波包分解能够提取到电流信号的突变成分。
小波分析技术可对磨削过程中的颤振进行识别[7],主轴性能评估也可采用小波包分解[8],Dugan[9]通过小波包分解进行不同频段信号的筛选分析,从而对调速电机的状态进行检测。从电机到主轴以及加工过程中的颤振,小波包分解在加工领域应用不断拓展,被广泛应用于电流信号的分析处理[10]。
小波包变换公式为[11]:
式中,x(t) 为经过预处理的电流信号;a为基小波的平移;b为基小波的伸缩。
从小波包分解公式可以看出,小波包分解通过基小波的伸缩、平移得到,而小波的伸缩和平移与基函数和分解层数有关,采用小波包分解有两个关键的问题需要解决,一个是合适的小波包基函数的选择,另一个是分解层数。根据不同小波基函数的特点选择八阶多贝西小波(db8 小波),db8 小波对频域的局部化能力很强,对突变信号较为敏感,频段不应过大,频段过大会导致频段内噪声信号含量多。结合信号的采样频率确定分解层数为7 层,分解层数为7 层时原始信号被分为了256个节点,最后一层分解将切削电流信号分成每段20 Hz的信息成分,可以将电流信号的主频、谐波分开。
2 实验设计
2.1 工件切削及信号采集
表面粗糙度受到加工过程的很多因素影响,其中主轴转速、进给速度对表面粗糙度作用显著,进给量能够直接对表面的峰谷造成影响[12],背吃刀量为0.5 mm,进给量为0.083 2 mm/r、0.145 5 mm/r 两种,主轴转速为40 r/min、212 r/min、410 r/min 3 种,实验加工参数的组合如表1 所示,机床切削实验如图2 所示。加工工件的车床为CA6130 车床,刀具为YT15 硬质合金刀,刀具型号为90°的弯头外圆车刀,收集交流电流信号的传感器为霍尔传感器,每加工一个工件通过示波器记录一次电流信号,采样频率为5 000 Hz,采样时间为2 s,每一次实验可以收集10 000 个电流信号数据点,机床停转后检测工件表面粗糙度,每组工况进行了30 组切削实验,一共进行了150 次实验,共150 组电流信号。

表1 加工参数和表面粗糙度

图2 机床切削实验
2.2 切削参数与表面粗糙度
加工条件和表面粗糙度如表1 所示。主轴转速和进给速度的表面粗糙度面响应图如图3 所示,切削速度高、进给速度低加工条件时工件表面粗糙度小,主轴转速超过一定转速或小于一定转速时表面粗糙度明显变小,主轴转速达到一定速度时即使继续提高转速,表面粗糙度也很难下降。另外进给速度对表面粗糙度影响也比较大,但是相比主轴转速进给速度对表面粗糙度的影响并不显著,当主轴转速很高时减小进给速度降低表面粗糙度的效果更好,从工况与表面粗糙度的角度出发,表面粗糙度受主轴转速与进给速度的影响较大。

图3 表面粗糙度的面响应
3 表面粗糙度的检测
3.1 电流信号特征的提取及筛选
由于表面粗糙度与主轴定子电流信号的联系并不清楚,为了避免遗漏电流信号中的表面粗糙度成分,先通过小波包分解将原始电流信号分成不同节点,节点较多特征维度比较大,需要过滤低相关性频段,电流信号能量特征能够判断机床切削能量变化,反映信号整体特点,可以作为挑选频段的依据之一。另外裕度因子与信号的冲击性有关[13],裕度因子可反映信号的局部特点与能量特征互相补充作为频段筛选的依据。
式中,E表示能量特征,Y表示裕度特征,Ii表示电流信号值,a表示特征值,b表示表面粗糙度。
如图4 所示,能量特征作为频段挑选依据时,并不是每个频段都与表面粗糙度存在很强的联系,与表面粗糙度相关性高的频段表现出正相关性,频段分布并不集中,较为分散。如图5 所示,裕度因子作为频段挑选依据时,较高相关性的频段并不都与表面粗糙度正相关,也存在负相关性频段,频段分布也是比较分散的,并不相邻,与能量特征挑选出来的频段并不重叠。保留能量特征、裕度因子作为挑选依据与表面粗糙度相关性最高的5 个频段。

图4 能量特征与表面粗糙度的相关性

图5 裕度因子与表面粗糙度的相关性
虽然仅保留10 个频段,但是如果盲目提取特征,特征的维度仍然较高,先提取频段重构后信号的峭度、偏度、均值、最小值、最大值、峰峰值、均方根、能量、标准差、振幅因数、波形因数、冲击因数、裕度因数13 个时域特征,及相应频域的13 个特征,每个节点一共提取26 个信号特征,共计260 个特征,采用随机森林算法对特征的重要性进行评估,进一步筛选特征,各个特征的重要性如图6 所示,不同特征的重要性有明显的区别,相当一部分电机电流信号特征与表面粗糙度无关,随机森林筛选的重要性前20 的电流信号特征占比之和高达33.2%,筛选留下的特征如表2 所示,重要性前20 的特征在各频段均有分布,在第16 个节点频段重要性特征最多,第16 个节点频段出现在小波包分解第四层,噪声含量较少。

表2 构建的特征

图6 特征的重要性
3.2 总谐波失真与积屑瘤
总谐波失真是指高次谐波幅值与基频幅值之比[14],高次谐波的幅值会迅速减小,最高只取基频的前5 次谐波,传感器测得的电流信号会存在一些误差,会对总谐波失真特征造成影响,需要进行改进。结合小波包分解提取各谐波及主频所在频段的能量,谐波能量之和与主频能量两者的比值为总谐波失真特征。
切削过程中,积屑瘤对表面粗糙度的影响较大,电流信号也会受到影响,积屑瘤尺寸大时,刀具前角增大,切削变得容易,但是积屑瘤是由切屑堆叠而成,稳定性差,会发生周期性的产生和消亡,发生破损时前角减小,切削变得困难,影响电流信号的稳定程度。总谐波失真特征可以评估主轴电流信号的稳定性,获取加工过程中积屑瘤的相关信息,如图7 所示,随着表面粗糙度的增加总谐波失真特征值明显增大。如图8 所示,总谐波失真特征值最大时对应中主轴转速,高主轴转速对应的总谐波失真特征值最小,可以通过总谐波失真特征判断加工过程的稳定性,获取工件的表面粗糙度信息。

图7 表面粗糙度和总谐波失真

图8 主轴转速和总谐波失真
3.3 能量特征
进给速度对表面粗糙度有显著的影响[15],经过互相关性挑选频段和随机森林的特征筛选发现能量特征对进给速度造成的表面粗糙度较为敏感。
图9 所示为进给速度的能量特征响应,能量特征为第7 个节点频段的能量特征。在最小进给速度表面粗糙度的能量特征并不是最小的,由于切削厚度过小,切削刃无法切入工件,造成刀具与工件强烈的挤压和摩擦,造成较小的进给速度能量特征也是比较大的。在中进给速度能量特征是最小的,此时切削刃完全切入工件,刀具与工件的挤压和摩擦较小,随后随着进给速度的增大能量特征逐渐增大,由于进给速度比较大导致刀具与工件挤压和摩擦比较大。进给速度的能量特征响应是U 型响应,表面粗糙度随进给速度的增大而增大,所以表面粗糙度的能量特征响应也是U 型响应。

图9 进给速度级别和能量
3.4 表面粗糙度分类
图10 所示为电流信号不同特征的散点分布。单个电流信号特征可能存在重叠,以至于无法准确区分表面粗糙度,多特征分析可以提高表面粗糙度的区分能力,不同特征与表面粗糙度的相关性存在较大差异,要结合多个特征才能完成对表面粗糙度的检测,提高表面粗糙度检测的泛化性。
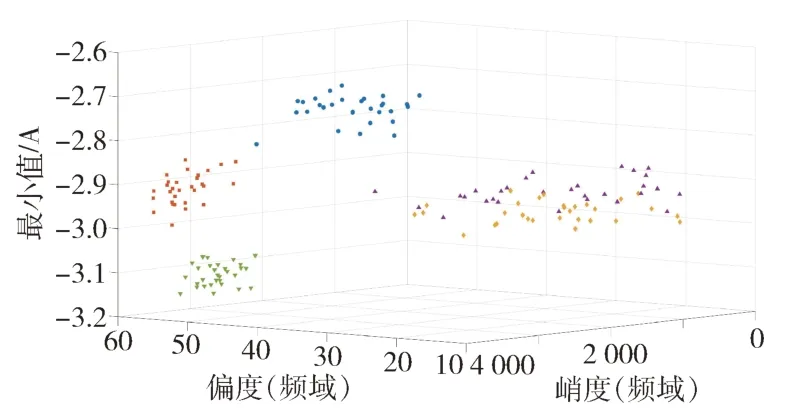
图10 不同表面粗糙度的特征散点分布
不同分类算法分类的准确率和时间如表3 所示,RF指随机森林算法对特征重要性进行评估,保留重要性较高的前20 个特征,PCA 是指采用主成分分析法对特征进行降维,PCA-SVM(主成分分析与支持向量机融合分类算法)、PCA-GNB(主成分分析与高斯朴素贝叶斯融合分类算法)对电流信号的表面粗糙度检测分类准确率比较低,而且分类时间比较长。RF-SVM(随机森林与支持向量机融合分类算法)、RF-GNB(随机森林与高斯朴素贝叶斯融合分类算法)对电流信号的表面粗糙度检测分类准确率较高并且检测时间较短,从侧面反映随机森林算法去除与表面粗糙度无关性特征的能力比较强。

表3 检测方法结果对比
RF-GNB 分类算法的混淆矩阵如图11 所示,将筛选的电流信号特征作为输入,标签为表面粗糙度级别一共分为5 类,只有一组数据被分类到相邻表面粗糙度类别中,时间仅有1.8 s,基本可以满足表面粗糙度的准确快速检测分类。

图11 高斯朴素贝叶斯分类的混淆矩阵
4 结论
主轴电流信号经过小波包分解之后,一些频段的重构信号和表面粗糙度相关性比较高,构造的特征工程可以实现表面粗糙度的快速准确检测,可有效避免因不符合表面粗糙度的工件浪费现象。主轴电机电流信号的总谐波失真特征可以检测积屑瘤,与加工稳定性相关,总谐波失真特征值越小加工过程越平稳。进给速度的能量特征响应类似于U 型响应,较小进给量时刀具与工件发生剧烈摩擦挤压,能量特征值偏大。
