基于MIAEKF的多温度下锂电池SOC估计

袁照凯，范秋华，王冬青，孙天民

（青岛大学电气工程学院，山东 青岛 266071）

目前，由于储能的重要性日益增加以及锂电池在各个领域中的广泛使用，锂离子电池的研究成为活跃且至关重要的课题。对电池性能的研究主要体现在材料工艺性能[1-4]和应用性能[5-8]上，在以电池管理系统(BMS)为代表的应用中，电池SOC 的估计，因其准确的预测决定了电池的有效使用并深刻影响着BMS 的高效运行，因此受到了世界学者的广泛关注。

目前，常用的估计SOC的方法如下：

（1）开路电压(OCV)方法：该方法根据从实验数据或OCV-SOC曲线拟合中获得的电池开路电压与SOC 之间的关系来估计SOC。这是一种直接而有效的方法，但需要静置一段时间后才能进行准确的OCV测量。因此，其使用范围有限。

（2）安时(AH)积分方法：此方法根据SOC 的定义，通过对一段时间内的电流进行积分来估算SOC。但是，由于传感器不准确和初始值的影响，它可能会累积误差。因此，它并不适合在锂电池长期充放电的工作环境中进行SOC估计。

（3）基于模型的方法：这些方法利用电池模型来估计SOC。主要分为电化学模型(EM)和等效电路模型(ECM)。EM 是一种基于电池内部化学反应和电化学特性建立的方法，耦合关系复杂，更适用于实验室分析而非BMS场景。ECM是一种常见的SOC 估计方法，因为它具有明确的物理含义和准确捕获电池动力学的能力[9]。滑膜观测器法[10]和H∞滤波法[11]都是基于此进行SOC 估计，但前者输出存在抖动，后者计算复杂。此外，ECM 易于表达以SOC 为状态的状态空间方程，因此可以使用卡尔曼滤波(KF)进行状态估计。由于锂电池的过程模型和测量模型都是非线性函数，无迹卡尔曼滤波(UKF)和扩展卡尔曼滤波(EKF)能够有效处理非线性系统的状态估计问题而被广泛用于锂电池的SOC 估计[12]。然而，UKF 需要权衡其计算复杂度、无迹点个数及权重等参数调整难度、采样点的选取以及对模型和数据的要求。EKF的估计精度对过程和测量噪声的初始值很敏感，因此容易出现发散，为此，Tian 等[13]运用自适应扩展卡尔曼滤波(AEKF)，实现噪声协方差矩阵的自适应匹配以优化滤波性能。双扩展卡尔曼滤波器(DEKF)可以在多时间尺度上联合估计电池状态和参数[14-15]。Li等[16]、Gu 等[17]介绍了多新息扩展卡尔曼滤波(MIEKF)及其改进算法，将当前时间的单一新息扩展到包含当前和先前时间步长信息的新息向量来改善过滤过程，误差信息的适量增加有助于更准确地估计SOC[18]。孙洁等[19]结合多创新的自适应扩展卡尔曼滤波算法对SOC 进行估算，取得了较好的估计效果。

（4）基于数据驱动的方法：随着机器学习技术和人工智能的进步，如循环神经网络(RNN)和长短时记忆网络(LSTM)方法逐渐应用在SOC 估计中[20-22]，通过捕捉电池充放电过程中的时序信息，从而实现高精度的SOC 估算。数据驱动的方法通常依赖于已有的充放电数据，并根据这些数据进行模型的训练优化进而进行预测。然而，电池的性能和行为受到多种因素的影响，例如温度、寿命、充放电速率、工况等。如果这些因素在历史数据中没有得到充分考虑，预测的精度可能会受到影响。

最近的研究主要集中在提高SOC 估计方法在各种条件下的准确性和自适应性，包括不同的温度条件和工况条件，正在努力开发能够处理参数变化和不确定性的自适应算法[23-26]。运用结合模型和数据驱动的双驱动方法[27-28]，或开创卡尔曼滤波算法与机器学习的集成算法等[29]，以确保在实际应用中实现可靠的SOC 估计。本工作通过函数模型引入MIAEKF算法，在保证估计精度的同时自适应温度变化引起的ECM 参数变化，实现了在多温度下良好的SOC估计效果。

1 电池建模

合适的电池模型是基于模型的方法实现锂电池SOC 精确估计的必要条件。等效电路模型结构相对简单、计算量小、精准度较好。

1.1 电池的电路模型

常见的电池等效电路模型主要包括Rint 模型、Thevenin 模型、双极化模型、PNGV 模型、GNL模型等[30]。本工作选择了结构复杂度适中、精度较高、易于结合估计电池SOC算法的双极化模型(又称为二阶RC电路模型)，如图1所示。

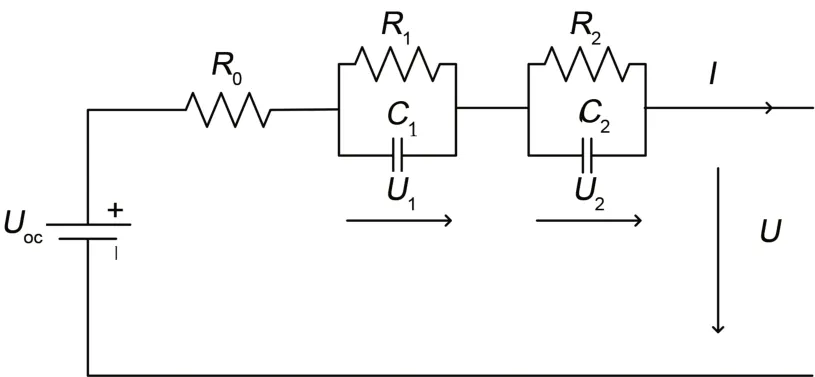
图1 双极化电池等效电路模型Fig.1 Dual polarization battery equivalent circuit model

由于形成的机理不同，电池的内阻可以划分为欧姆内阻和极化内阻，欧姆内阻等效为离子在运动过程中受到的阻力，用电阻R0来描述。极化内阻来源于材料自身的特性，可细分为电化学极化内阻和浓差极化内阻，用阻容网络R1C1、R2C2来描述[31]。U为电池端电压，I为电池端电流，规定的电流方向放电为正，充电为负。

根据基尔霍夫电压定律，k时刻端电压为：

对阻容网络R1C1、R2C2的电压全响应包括零状态响应和零输入响应：

式中，Ik-1表示k-1时刻的电流；U1,k-1、U2,k-1表示k- 1时刻的电压；Ts表示k-1时刻到k时刻的采样时间；时间常数τ1=R1C1，τ2=R2C2。

则电压全响应：

由SOC 的定义可知，k时刻的SOC 可以表示为：

式中，η表示通过充放电实验获得的充放电效率，通常，充电时η= 1，放电时η＜1；QN表示电池额定容量或最大可用容量。由双极化等效电路模型可知锂电池的状态变量设置为xk=[U1,k,U2,k, SOCk]T；

则由公式(2)～公式(5)可知，带有过程噪声wk-1的电池状态空间方程可以写为：

式中，wk-1表示均值为0、协方差矩阵为Qk-1的噪声，即wk-1～(0,Qk-1)。

由式(1)可得带有观测噪声vk的观测方程：

式中，vk表示均值为0、协方差矩阵为Rk的噪声，即vk～(0,Rk)。

1.2 不同温度下的ECM参数辨识

本工作实验数据来自于McMaster 大学公开的锂离子电池测试数据集，该数据集提供了多个温度条件下的多种测试工况的锂离子电池充放电数据[32]。由数据集中每个温度条件下的混合动力脉冲能力特性(hybrid pulse power characteristic，HPPC)实验工况测试数据，可以得到不同温度下的不同SOC 阶段对应开路电压(OCV)的值。对相同SOC 下的OCV 取平均值，通过多项式函数拟合，可以得到多温度下的SOC-OCV 曲线，如图2所示。

图2 多温度下的SOC-OCV曲线Fig.2 SOC-OCV curves under multiple temperature conditions

由于在ECM中的电池参数与电池当前SOC和温度有关，为了保证SOC 估计精度，分别对不同温度下电池的不同SOC阶段进行相应的参数辨识。应用FFRLS 对锂电池在-10 ℃、0 ℃、10 ℃、25 ℃、40 ℃条件下的洛杉矶92(LA92)工况测试数据进行参数辨识，得到在不同温度条件下不同放电程度时R0、R1、C1、R2、C2的值。

由二阶RC 等效电路模型可以推出其在复频域中的输出方程为：

令E(s)=Uoc(s)-U(s)，则电池模型的传递函数可以表示为：

式中，G(s)代表电路阻抗；τ1、τ2表示极化时间常数，τ1=R1C1，τ2=R2C2。根据双线性变换原理

式中，T表示采样时间，离散化G(s)可得

式中，α1、α2、β0、β1、β2表示待定系数，则时域离散化表达为：

将公式(12)变换为最小二乘法的形式：

则

由式(13)估算出θ的最优估计。由式(9)～式(11)可得模型参数求解公式如下：

在不同温度条件下测试HPPC 工况的放电数据，SOC=100%时的离线参数辨识结果如表1 所示，作为FFRLS辨识过程的初值。

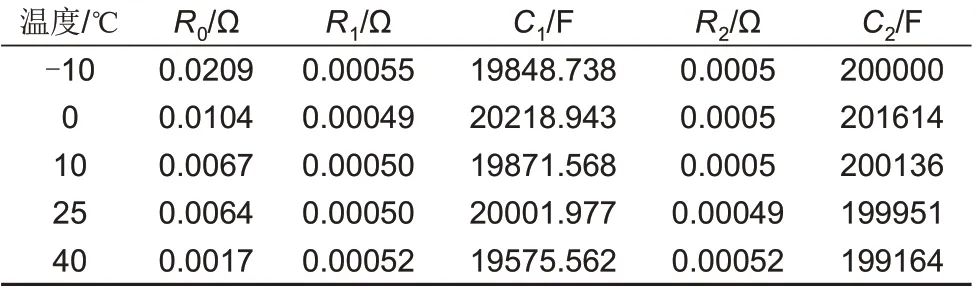
表1 SOC=100%时HPPC的参数辨识结果Table 1 Parameter identification results for HPPC at SOC=100%

电路参数与SOC、T存在非线性关系，将辨识结果的离散点作为样本点利用Matlab 软件进行插值拟合得到关系式(15)，函数模型拟合效果如图3所示。

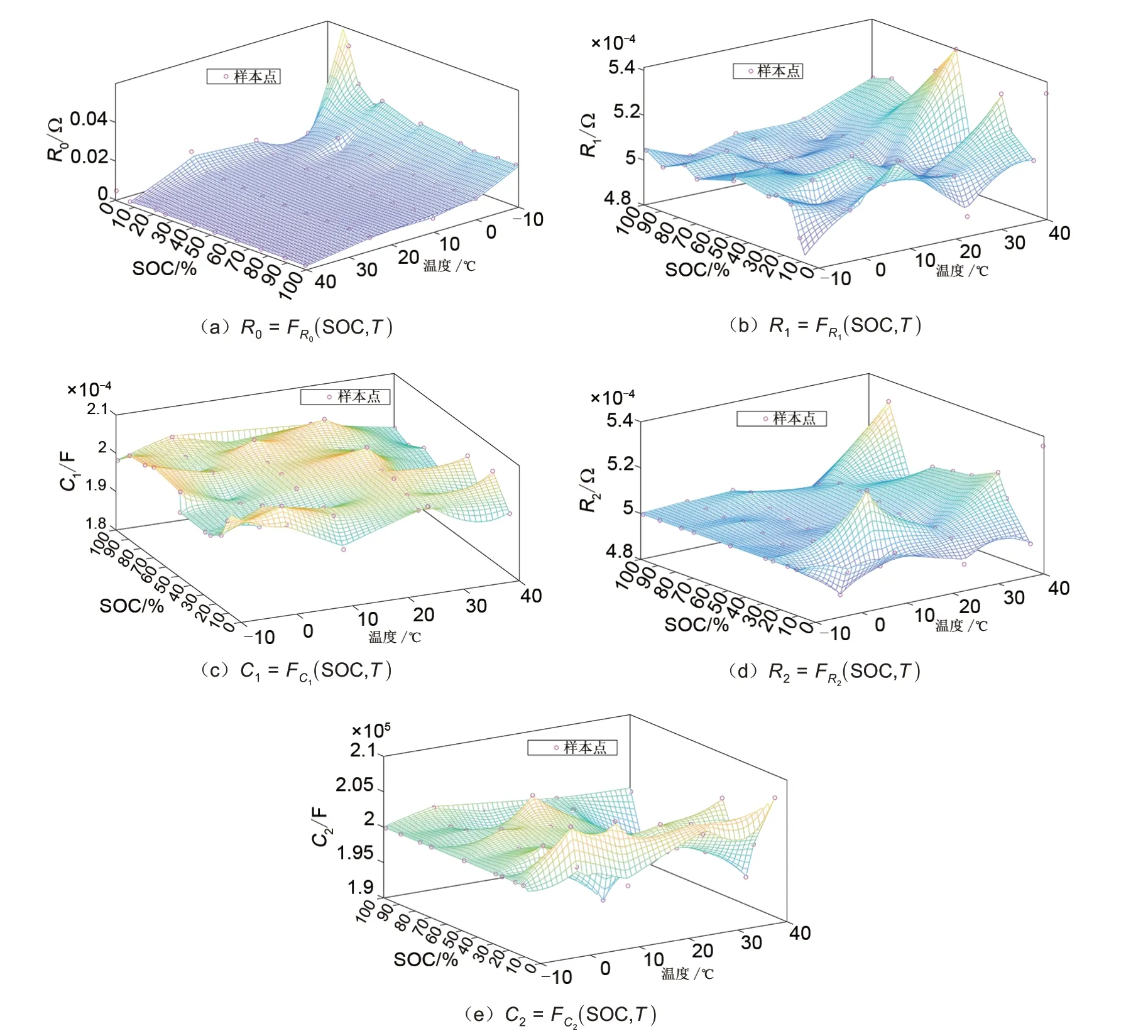
图3 电路参数R0、R1、C1、R2、C2与SOC、T的三维拟合效果图Fig.3 The 3D fitting effect graph of circuit parameters R0, R1, C1, R2, and C2 with respect to SOC and temperature (T)

选取40 ℃下的LA92工况数据对参数辨识结果的精确性进行验证。由图4可知参数辨识结果具有较高精确性，为下文SOC 估计提供了精确的电池模型。

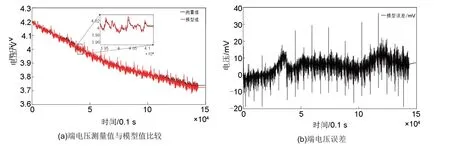
图4 40 ℃下的LA92工况数据模型验证效果Fig.4 Verification results of the LA92 driving cycle data model at 40 ℃

2 基于MIAEKF的状态估计

2.1 多新息自适应扩展卡尔曼滤波(MIAEKF)算法

由于电池充放电是一个非线性过程，因此用卡尔曼滤波估计电池SOC 时需要用泰勒公式将非线性数学模型进行展开并去掉高阶项来线性化模型。上文式(6)、式(7)可以简化表达为如下形式：

将f(·)、h(·)分别在k-1 时刻的状态后验估计值处、k时刻的状态先验估计值处展开得：

因此，当已知k-1 时刻的后验估计值x̂k-1与状态向量的协方差矩阵Pk-1时，k-1 到k时刻的状态向量先验估计值可以表示为：

相应先验状态协方差:

则此时的新息为：

计算卡尔曼增益：

状态协方差更新：

本工作在EKF算法中通过构建滑动窗口，分别用其中的残差数据、新息数据自适应更新窗口最新时刻的协方差矩阵[33]，用开窗平均的方法代替传统自适应因子的构建，并融合多新息理论，将窗口的均值新息数据乘以合理的新息均值系数用于卡尔曼滤波的后验估计之中。

当窗口长度为a时，且k时刻之前的历史数据点数大于a时，令

式中，λ代表窗口长度内新息的均值系数，对估计精度存在一定影响。

k时刻的后验估计状态更新：

观测值后验估计值：

后验残差为：

令

通过k时刻之前窗口内的新息数据、残差数据，自适应调节协方差矩阵Q、R。

式(19)～式(30)体现了MIAEKF 算法的具体内容。算法流程图如图5所示。

简易水位站即为水尺桩，可采用木质、石质或不锈钢材质。对于无条件建桩的监测站，选择在离河边较近的固定建筑物或岩石上标注水位刻度；水位监测尺的刻度以方便监测员直接读数为设置原则，并根据各监测点实际情况，标注预警水位。在河南、陕西等省，为了方便预警，直接在水尺上标注两个预警水位，而不标注水位刻度。

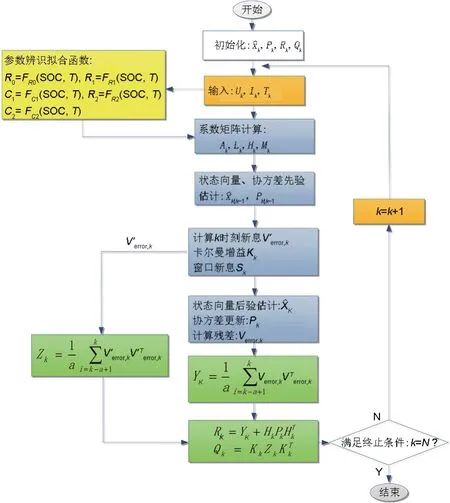
图5 MIAEKF算法流程图Fig.5 The steps of the MIAEKF algorithm

2.2 实验数据数值验证

2.2.1 算法性能验证

为验证MIAEKF的有效性，首先应该找到最优的自适应窗口长度a的值，并在此基础上讨论引入多新息均值来提高估计精度，以及合理的新息均值系数λ。

将MIAEKF 算法中的式(25)、式(26)处，改写为单新息后验估计：

在40 ℃ LA92 工况下，验证单新息AEKF 算法，并讨论窗口长度a的值对估计精度的影响。分别验证a=15、25、50、100、200 时的SOC 估计精 度 。 以 SOCerror的 均 方 根 (RMSE =n为数据长度)、最大估计误差(Maxsocerror)为参考指标，寻找最优窗口值，结果如表2所示。

表2 不同窗口长度下AEKF估计精度Table 2 Estimation accuracy of AEKF for different window lengths

图6表明了在不同窗口长度下AEKF的SOC估计效果，由表2 及图6 可以看出，在a=25 时SOC的估计精度相对较高。

设置a=25，分别验证MIAEKF 算法中窗口新息均值系数λ= 0.5、1、2、3、4、5 时的估计精度，结果如表3所示。

表3 a=25条件下不同λ时MIAEKF SOC估计最大误差Table 3 The maximum error of MIAEKF SOC estimation for different λ under a=25

由上述数据可知，当a=25、λ=2时MIAEKF算法具有较好的SOC估计精度。

在此参数条件下，用40 ℃下的LA92 工况数据，对比EKF、AEKF、MIAEKF算法的SOC估计效果，如图7所示。

图7 EKF、AEKF、MIAEKF算法估计效果Fig.7 SOC estimation performance of EKF, AKF, and MIAEKF algorithm

表4 不同SOC估计算法数据对比Table 4 Comparison of data for different state of charge (SOC) estimation algorithms

2.2.2 不同温度下基于MIAEKF的SOC估计

分别对电池在城市驱动台车(UDDS)工况下，对在-10 ℃、10 ℃、25 ℃条件下的电池实验数据利用MIAKEF 算法进行SOC 估计，以验证MIAEKF 算法在不同温度下SOC 估计的有效性，结果如图8所示。算法的输入参数为端电压、端电流和温度，在估计过程中经公式(15)调整与温度、SOC相关的ECM参数，进而更新系数矩阵，以此来适应不同温度下的SOC估计。

图8 MIAEKF在UDDS工况不同温度下的SOC估计Fig.8 MIAEKF-based SOC Estimation at Different Temperatures under UDDS Conditions

由图8 可知，在不同温度下MIAEKF 具有良好的估计效果，估计误差均在±0.8%以内。而上述SOC估计是基于公式(15)进行的，验证算法的三种温度条件都在公式(15)中有所体现。为进一步验证多温度条件下函数拟合应用在SOC 估计算法的效果，将对锂电池在-10 ℃、0 ℃、25 ℃、40 ℃条件下的LA92 工况放电数据进行参数辨识结果的离散点作为样本点利用Matlab 软件进行插值拟合得到关系式：

将算法中的公式(15)替换为公式(32)，其中并不体现10 ℃条件下的参数辨识结果。对电池分别在HWFET、LA92、Mixed 三种工况10 ℃条件下的电池测试数据进行SOC 估计。以此验证多温度条件下算法的实用性。

由图9可知，函数所用的拟合点并不包括10 ℃时的参数辨识结果，在10 ℃ LA92、HWFET、Mixed三种测试工况下该算法的SOC估计均表现出了较为良好的效果，估计误差均在±1%以内。

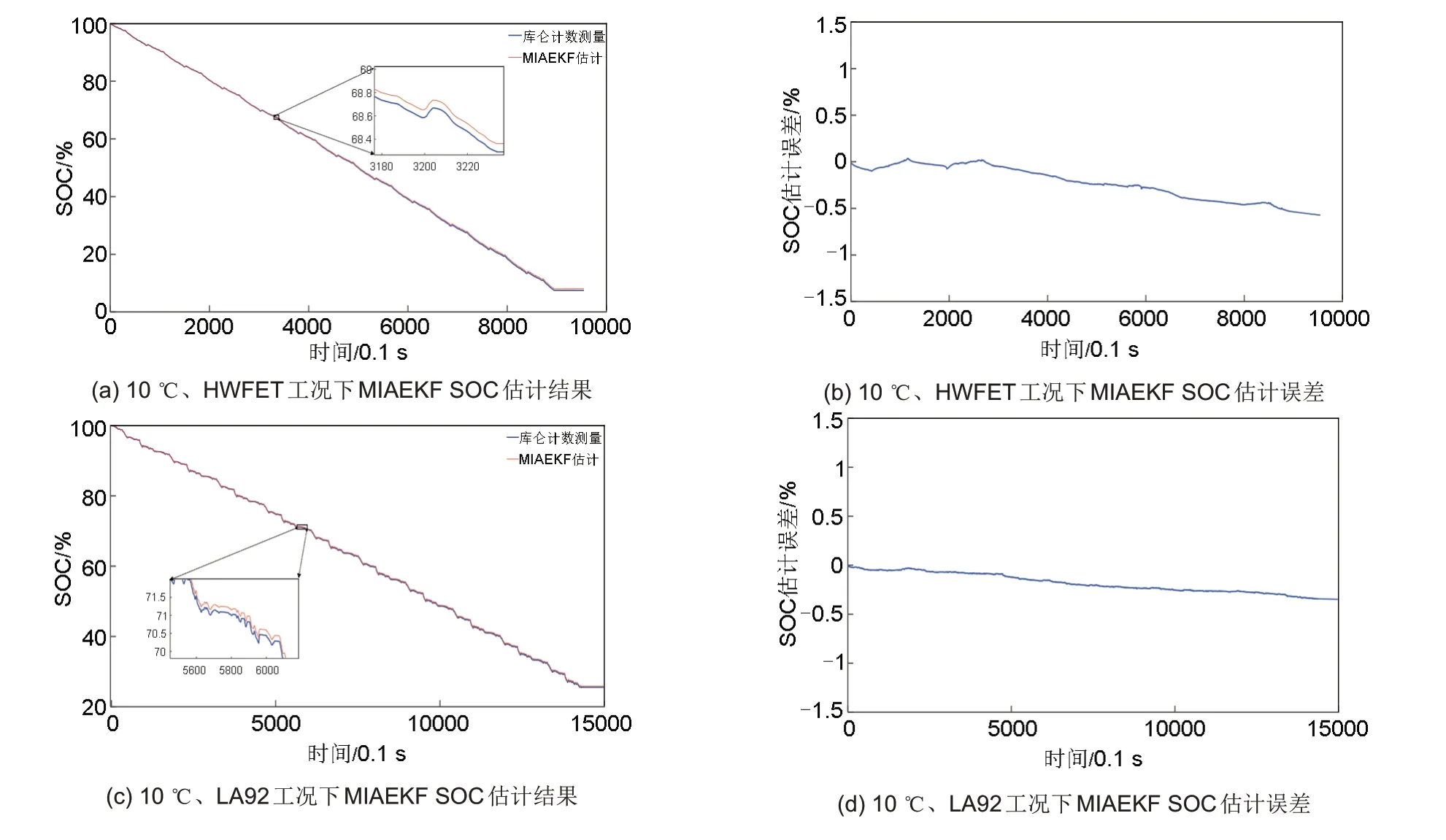
图9 10 ℃ HWFET、LA92、Mixed工况下MIAEKF算法SOC估计Fig.9 SOC estimation under different testing conditions at 10 °C

3 结 论

在锂电池双极化模型的基础上，通过对锂电池在不同温度下的实验数据利用FFRLS 进行参数辨识的结果，进行模型参数关于温度与SOC 的二维函数拟合。在MIAEKF算法中引入拟合函数，使在状态估计过程中能够更新参数，以适应不同温度下的SOC估计。在较合适的初始参数条件下，a=25、λ=2 时MIAEKF 相较于EKF、AEKF 具有较好的估计精度。分别对-10 ℃、10 ℃、25 ℃环境下UDDS工况的数据进行验证，三种不同的温度环境下SOC 估计误差均在±0.8%以内。为进一步验证拟合函数在多温度下的有效性，尽管10 ℃下的参数辨识结果不作为拟合点，得到的拟合函数运用在算法中，在10 ℃ LA92、HWFET、Mixed 三种测试工况下进行数据验证，估计误差均不超过±1%。这为多温度下的SOC估计提供了一种方法。