抗风缆对人行悬索桥荷载试验的影响分析

陈挚 CHEN Zhi

（同纳检测认证集团有限公司，上海 200000）

0 引言

悬索桥是由主缆、索塔、加劲梁、吊索、锚锭及抗风缆构成的组合体系。主缆是悬索桥的主要承重构件，在恒载作用下主缆具有很大的初张力，为结构提供强大的“重力刚度”并使得自身维持一定的几何形状，在活载作用下主缆可以通过自身几何形状的改变来影响结构的平衡状态，具有较强的非线性力学特征。由于人行悬索桥的特点，其跨度较大且自身结构轻柔，一般会布置抗风缆增加桥梁对风荷载的抵抗能力并可以在一定程度上提高桥梁刚度。同时考虑到人行悬索桥的加劲梁自重普遍较轻，导致结构的“活载-自重比”较高，造成人行悬索桥在静载试验中会呈现出较强的几何非线性。若按简化算法不考虑抗风缆对桥梁的刚度影响或不考虑试验荷载对桥梁结构的非线性影响，则计算结果无法精确指导桥梁检测工作。

文章以某人行悬索桥为研究对象，分析不同抗风缆状态对桥梁检测工作的影响，以期为桥梁检测提供可靠的理论依据。

1 抗风缆对桥梁动力特性及结构刚度的影响

抗风缆有以下几种形式：与桥面系夹角θ=0°的平行式，θ=45°的左右分张式，θ=90°的垂直式以及内敛式和斜拉式[1]。将抗风缆与桥梁加劲梁的连接简化为有刚度的弹性支撑，在不考虑桥梁结构阻尼影响的情况下，对图1 所示计算模型采用连续弹性梁方法进行动力特性近似分析，梁的基频计算采用瑞利法近似求解[2]。

图1 计算模型简图

式中：ω 为结构的基频；ρ 和E 为材料的密度和弹性模量；A 和J 为弹性梁的面积和惯性矩；Y（x）为弹性梁的挠度曲线；ki为抗风缆的竖向刚度，与抗风缆的水平力大小和抗风缆的夹角相关；xi为抗风缆与弹性梁的连接位置。

由上式可知，当抗风缆与桥面系夹角θ≠0°时，抗风缆在一定程度上可以提高桥梁的竖向基频，即增加结构的竖向刚度。

2 依托工程

2.1 工程背景

某人行悬索桥为主跨120m 悬索结构，主缆线形按抛物线确定，矢跨比1/12，主跨120m，矢高10m；风缆矢跨比取1/30，与水平面夹角30°。单侧主索选用7 根306×19S+IWR 型钢丝绳，塔顶主索和背索水平夹角相同。索塔采用门字形钢筋混凝土结构，塔顶设置索鞍；索塔基础为人工挖孔桩基础；锚碇系统为重力式锚碇。

主索采用直径30mm6×19S+IWR 型钢丝绳，一根主索7 根钢丝绳，钢绳直径30mm，钢芯，AB 级镀锌，公称抗拉强度1670MPa。抗风主索规格为6×7S+FC 型，直径30mm；抗风拉索规格为6×7S+FC 型，直径16mm，AB 级镀锌，公称抗拉强度1670MPa。

全长171.2m，桥梁净宽2.0m，全宽2.3m，桥梁设计荷载等级为人群荷载：3.5kN/m2。桥型布置见图2 所示。

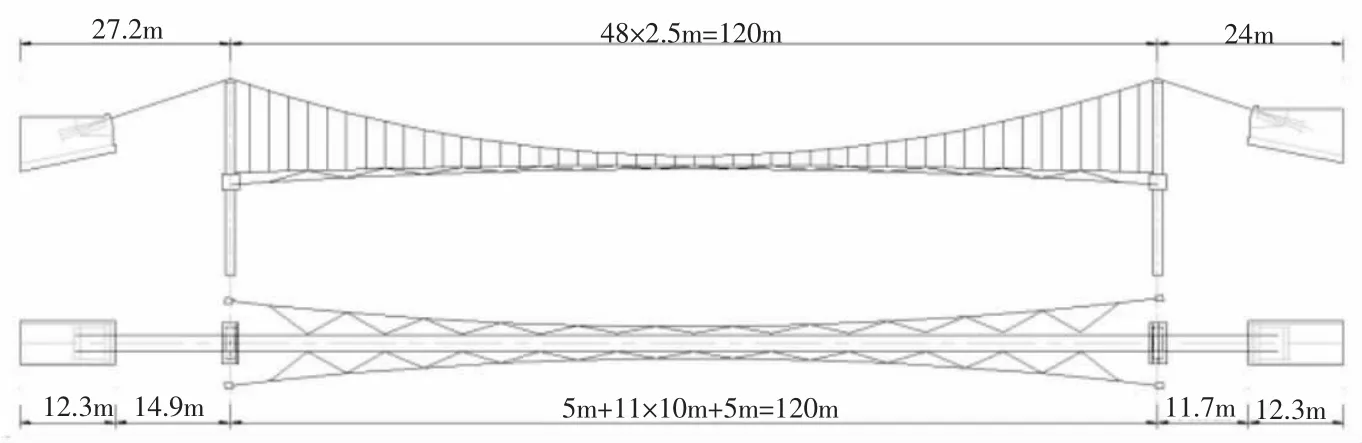
图2 某人行悬索桥桥型布置图

2.2 加载方案

为准确模拟人群荷载的静力效应，试验一般采用水箱或水袋进行加载。由于人行悬索桥结构较轻柔，在试验荷载作用下桥面结构会产生较大的竖向变形，而水箱或水袋中的加载水会随结构变形而流动，导致试验荷载出现非线性变化。为减小试验荷载的非线性变化，试验水箱或水袋应增加纵、横向隔板，合理划分仓室。本次试验水箱全长120m 宽2m，在长度方向上设置47 处隔板，宽度方向上设置1 隔板，合计分为96 个仓室，每个仓室长2.5m 宽1.0m。

考虑到人行悬索桥结构的刚度会随着活载的变化而发生显著变化，因此静载试验可采用“多分步，少加载”的方式进行，即：结构满载前多分级，降低每级的加载长度和加载吨位，分析各测点在整个各级荷载作用下的变化趋势和规律。

2.3 有限元模型

采用Midas Civil 建立全桥三维有限元模型，其中加劲梁、主塔、横梁采用梁单元模拟，主缆、吊杆、风缆采用索单元模拟，边界条件采用一般约束和弹性连接，主塔索鞍在施工阶段释放纵向约束，在成桥阶段锁定。

为分析抗风缆对桥梁荷载试验的影响，本次模拟采用四种方式进行模拟，对桥梁结构进行敏感分析，并对比实测数据和有限元计算结果。

方式一：建立无抗风缆全桥模型。

方式二～方式四：建立有抗风缆全桥模型，抗风缆与桥面系夹角成30°，抗风缆水平张力分别为138kN，256kN（设计要求状态），530kN。

有限元模型见图3，图4。

图3 方式一无抗风缆有限元模型

图4 方式二～方式四有抗风缆有限元模型

3 抗风缆对桥梁自振特性检测的影响分析

在桥梁检测工作中，结构自振特性是重要的评定标度，关系着桥梁的检算系数和检算结果。同时，悬索桥的自振特性分析与其他类型桥梁不同，直接关系到悬索桥结构的安全[3]。通过敏感分析分析，得到无抗风缆、有抗风缆以及不同抗风缆水平张力下的结构关键振形和关键频率，见表1，各振型模态频率关系分布图见图5。

表1 结构关键自振特性计算结果

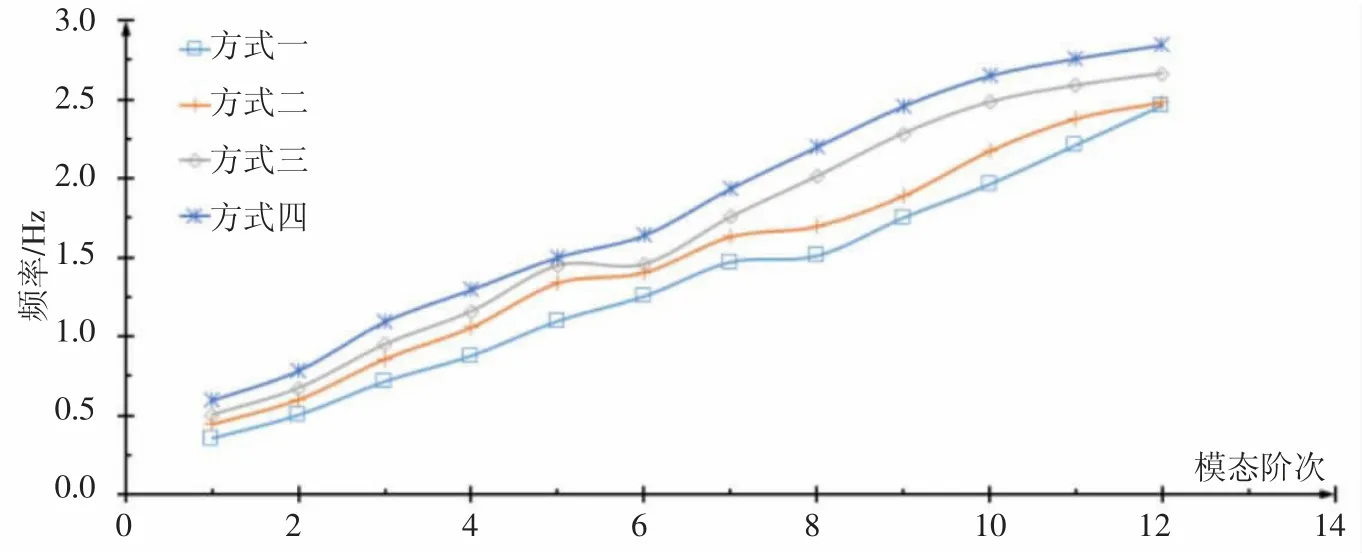
图5 竖弯模态-频率关系分布图

在该桥主跨跨中布置竖向拾振器，实测该桥一阶正对称竖弯基频为0.55Hz。

由上述图表可知：①该桥在3Hz 内存在约12 阶竖弯模态表明大跨径人行悬索桥的竖弯模态十分密集；②考虑抗风缆对桥梁结构的作用时，计算的结构竖弯、扭转和平弯自振频率均明显提高，且随着抗风缆水平张力的提高桥梁自振频率也随之提高。表明抗风缆会影响桥梁结构竖向刚度，抗风缆成桥水平张力与桥梁结构竖向刚度呈正相关；③该桥实测一阶正对称竖弯基频介于无抗风缆理论值（方式一）和抗风缆水平力138kN 理论值（方式二）之间，表明该桥抗风缆存在松动未达到设计要求状态（抗风缆水平力256kN）与现场检查结果基本一致。

4 抗风缆对桥梁静载试验的影响分析

4.1 抗风缆对加劲梁挠度的影响

结构挠度测量是桥梁静载试验中的重要检测项目，《公路桥梁承载能力检测评定》（JTG/T J21-2011）规定：试验荷载作用下主要测点的校验系数不得大于1，否则可判定桥梁承载能力不满足要求，因此合理的理论值是计算出准确校验系数的前置条件。

分别采用不同模拟方式和分析方法计算该桥加劲梁在试验荷载下的各级挠度值，并与主要测点实测值进行比对见表2 和图6，图7。

表2 加劲梁挠度值对比表单位：mm

图6 各工况下L/2 测点挠度理论-实测对比图

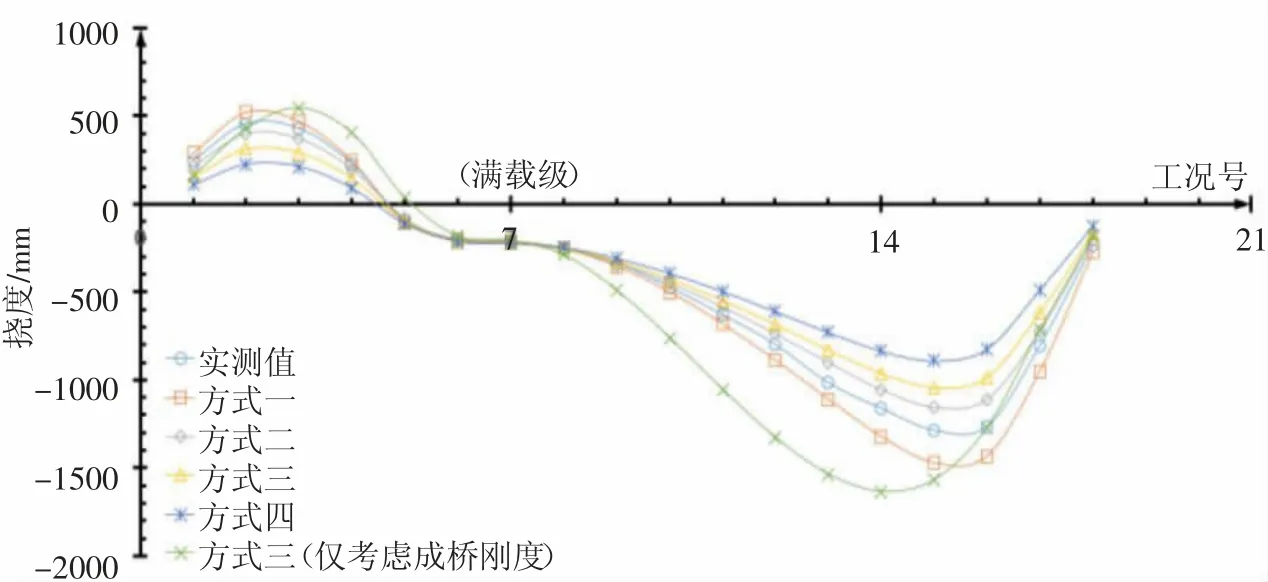
图7 各工况下L/6 测点挠度理论-实测对比图

由实测结果与理论计算可得：①方式三（仅考虑成桥刚度）计算的各主要测点在桥梁静载试验中的变化趋势与实测结果存在较大偏差，其主要测点的最大挠度级与实测不一致，难以指导检测工作；②方式一～方式四计算的主要测点挠度值在桥梁满载情况下偏差较小，但随着桥梁加、卸载各模拟方式的计算偏差逐步增加，尤其在桥梁处于非对称荷载的情况下（第7 级卸载～第10 级卸载）计算偏差最大；③桥梁主要测点实测值在静载试验中的变化趋势与按方式一～方式四分析的理论趋势一致，实测结果介于无抗风缆理论值（方式一）和抗风缆水平力138kN 理论值（方式二）之间，与自振特性检测结果吻合。

4.2 抗风缆对加劲梁梁端纵向位移的影响

人行悬索桥多为漂浮或半漂浮体系，在梁端采用有限位移铰支座释放加劲梁的纵向变形。抗风缆拉索一般与桥梁纵向呈一定夹角，在加劲梁受荷变形时抗风缆的内力和几何状态也会随之变化，进而在一定程度上约束加劲梁的纵向位移。考虑到有限位移铰支座和梁端伸缩缝装置的允许滑动量有限，在桥梁荷载试验期间应密切监测加劲梁梁端位移，防止支座破坏。

分别采用不同模拟方式和分析方法计算该桥加劲梁梁端在试验荷载下的纵向变形最大值，并与实测值进行比对见表3。

表3 加劲梁梁端纵向位移对比表单位：mm

由表3 可得：①无抗风缆模型（方式一）计算的荷载试验期间梁端最大纵向位移值与实测结果存在严重偏差，难以指导检测工作。表明人行悬索桥抗风缆对静载试验期间加劲梁纵向变形影响较大；②有抗风缆模型（方式二～方式四）计算的静载试验期间梁端最大纵向位移值随着抗风缆成桥内力的增加而逐步减小。表明抗风缆成桥内力大小与加劲梁纵向约束效果呈正相关。

5 结束语

本文以某人行悬索桥为研究对象，分析不同抗风缆状态对桥梁检测工作的影响，得出以下结论：①人行悬索桥抗风缆内力状态不同对桥梁静载试验期间的理论值存在较大影响，因此理论计算时需考虑抗风缆对桥梁的刚度影响以及试验荷载对桥梁结构的非线性影响。②对存在抗风缆的人行悬索桥，可先进行自振特性检测，分析抗风缆对桥梁结构的刚度影响，进而修正理论模型，指导后续检测工作。③人行悬索桥抗风缆对静载试验期间加劲梁纵向变形影响较大，且抗风缆成桥内力大小与加劲梁纵向约束效果呈正相关。因此，对抗风缆松动或未设置抗风缆的柔性人行悬索桥，在静载试验期间应密切监测梁端位移，防止纵向位移过大对桥梁伸缩缝装置或加劲梁支座造成破坏。