内生全要素生产率、经济波动与通货膨胀

张伍涛 盘业哲 姚金海

（1.湖州学院经济管理学院，浙江湖州 313000；2.广州开发区战略研究院，广东广州 510670）

一、引言

随着中国经济迈入高质量发展阶段，技术创新已然成为中国迈向科技强国和制造大国的重要驱动力。中共十九大提出了创新是引领发展的第一动力，为中国经济高质量发展赋能。中国经济增长的科技驱动力已经逐步实现自主研发，技术创新不断成为现代化经济体系的重要支撑。一般而言，技术创新伴随着生产力的提高，表现为全要素生产率的提高（唐未兵等，2014）。[1]如图1 所示，中国R＆D经费增长率和全要素生产率表现出显著的顺周期性，劳动生产率和全要素生产率相对R＆D 经费增长率存在一定时滞，以上表明中国技术创新和全要素生产率存在顺周期的特征，经济增长、全要素生产率的变化落后于技术创新。在面对金融危机、欧债危机、供给侧结构性改革和新冠疫情等外部冲击时，劳动生产率和全要素生产率表现出一致的变化趋势，表明全要素生产率中存在的内生成分促使其在受到外生冲击后保持与GDP 增长率相近趋势。因此，通过构建一个引入内生全要素生产率的中等规模标准DSGE 模型，将全要素生产率的外生成分和内生成分分离并分别研究其对经济变量的影响，尝试阐述内生全要素生产率的机制和中国经济增长背后的内生驱动因素。

图1 2001—2020年中国劳动生产率、TFP增长率及R＆D支出增长率

二、文献述评

国内外学者就全要素生产率对经济增长的影响展开了广泛探讨。有学者将全要素生产率作为经济增长的重要测度指标并研究其影响因素。在此类研究中，全要素生产率被抽象化为广义技术进步，是连接技术进步和经济增长的主要桥梁。苏治和徐淑丹（2015）发现TFP中的技术创新成分对经济增长产生了显著的促进作用，是中国经济高速发展的重要驱动力。[4]程名望等（2019）通过测算中国经济增长中各项因素的贡献率，发现市场潜能的贡献率最高，TPF 的贡献率为20.03%。[5]陈彦斌等（2019）研究发现，人工智能技术的发展有助于缓解人口老龄化对全要素生产率的不利影响，减少老龄化对经济增长的负面冲击。[6]通过对全要素生产率的分解，刘志彪和凌永辉（2020）实证分析经济结构转换对TFP的影响呈现出先促进后抑制的倒U型关系，TFP的提升有助于提升中国经济集约化程度。[7]贾洪文等（2021）使用绿色全要素生产率作为经济高质量发展的代理变量，研究发现地区科技水平的提升有助于促进经济增长。[8]随着经济发展模式的转变，中国提升全要素生产率的主要途径是实现从依靠技术模仿和要素流动到部门内竞争性技术创新的转型（江飞涛等，2014；刘世锦等，2015）。[9，10]

研究全要素生产率影响经济增长的另一个方向是将全要素生产率作为技术进步的代理变量，并在宏观经济模型中将其假定为一种完全外生的技术冲击。其中最为经典的代表是以Smets ＆ Wouters（2003）、Christiano et al.（2005）所构建的新凯恩斯模型，学者研究技术冲击对经济变量的影响大多基于NK 模型。[11，12]一般而言，单位正向技术冲击对GDP 增长有显著的促进作用（余泳泽和张先轸，2015；朱军，2017）。[13，14]虽然将全要素生产率抽象化为广义技术进步有助于简化模型和增强理论分析的严谨性，但全要素生产率并不完全等同于技术进步，狭义技术进步与全要素生产率之间存在较大差异（唐未兵等，2014）。除了狭义技术进步外，影响全要素生产率的因素还包括诸如制度、市场化程度、对外开放、资源错配、产业结构等。因此，全要素生产率中存在的内生成分应该被识别出来，以全面分析其对经济增长的影响。一些关于金融危机发生后关于生产率的研究对此提供了间接证据。Hall（2014）和Reifschneider et al.（2015）分析了全球金融危机后经济衰退期间美国商业投资的崩溃对资本存量和生产率的影响，认为生产率持续下降是技术投资减少的结果，也是经济衰退的内生反应，衰退期经济活动收缩反过来导致了产出增长的内生下降。[15，16]

在宏观经济模型中，一种解决全要素生产率内生化的方法是放松标准的外生技术假设并内生地模拟全要素生产率增长，这种引入内生全要素生产率的方法是建立在Romer（1990）提出的内生增长理论基础上。[17]Comin ＆ Gertler（2006）在内生增长理论基础上通过研发和使用内生技术构建了一套内生全要素生产率的机制，并考虑商业周期和技术采用的内生途径。[18]Moran ＆ Queralto（2018）使用具有内生全要素生产率的新凯恩斯主义模型来量化由于零下限利率（ZLB）货币政策约束导致的TFP 损失及比当前预期更慢的速度收紧货币政策的TFP收益。[19]Bianchi et al.（2019）构建了包含债务和股权融资摩擦的内生化TFP 的宏观经济模型，发现股权融资冲击对研发投资放缓的解释力更强。[20]Anzoategui et al.（2019）进一步优化了模型中扩散过程中的滞后现象并考虑了约束性零下限利率的货币政策，研究发现全球金融危机后的经济衰退中美国生产率下降大部分源于内生现象，内生全要素生产率机制也有助于解释经济衰退前的生产率下降。[21]

技术研发的溢出效应表明全要素生产率增长与经济状况之间存在内生关系（Schmöller ＆Spitzer，2021）。[22]综上，本研究可能的边际贡献为：一是区别于以往研究中将全要素生产率作为外生冲击或者不区分内生成分和外生成分，通过在技术研发和采用过程将全要素生产率内生化，考虑经济增长中的内生全要素生产率机制；二是基于新凯恩斯模型构建涵盖内生全要素生产率的DSGE 模型，对内生全要素生产率影响经济增长的理论机制作出解释。

三、内生全要素生产率机制下的DSGE模型

（一）家庭部门

在Smets ＆ Wouters（2007）的模型中，假设代表性家庭的消费行为受到消费习惯的影响，家庭的储蓄全部投资于资本和无风险债券，将投资于资本的储蓄全部出借给中间产品生产商。由于存在工资黏性，家庭实质上相当于不同类型劳动力的垄断竞争供应商。[23]假设代表性家庭作出最优行为决策时受劳动力供给和流动性偏好的影响。首先家庭为其他部门提供两种劳动力，用于研发部门和技术使用的熟练劳动力Lhs，t及用于生产中间产品的非熟练劳动力Lhu，t。假设代表性家庭更偏好于持有安全性更高的资产，即家庭有较高的流动性偏好，在家庭效用函数中引入债券持有量。参考Fisher（2015）将流动性需求冲击ρliquid,t引入模型，该冲击是经济周期性波动的主要成因，具有金融冲击的传递特性。Ct表示t期消费，Bt表示无风险债券持有量，Πt表示投资于垄断竞争企业所分得的利润，Kt表示资本，Qt表示资本价格，Rkt表示资本回报率，Dt表示资本租金率，其中Rkt=DtQt/Qt-1。因此，代表性家庭的最优决策问题可以表示如下：

代表性家庭的预算约束为：

因此，可以得出资本Kt和无风险债券Bt的一阶条件分别如下：

其中，Ξt，t+1表示家庭随机贴现因子，ξliquid，t表示单位消费的流动性偏好冲击，分别由和决定，其中，表示单位消费的边际效用。

式（4）中的流动性需求冲击对无风险债券的一阶条件造成扭曲，对既定的无风险利率Rt+1，ξliquid，t上升导致家庭增加预防性储蓄，即家庭通过减少消费以降低家庭随机贴现因子Ξt，t+1来实现无风险债券的一阶条件。由式（3）和式（4）得到式（5），表明流动性需求的冲击导致利差Rkt+1-Rt+1的增加，降低了投资需求，对消费和投资产生负向影响，展示了金融冲击传导机制的相似性。

（二）最终生产商

参考Anzoategui et al.（2019）的作法，在生产结构中引入内生全要素生产率并展示其在模型中的动态演化。假设经济中存在两种企业类型：中间产品生产商和最终产品生产商。垄断竞争的最终产品生产商i 生产差异化产品的Y it，最终产品的总产出Yt是差异化产出Y it的CES函数：

其中，μt＞1 是外生的。假设最终产品生产商i使用中间产品投入组合进行生产是其唯一的生产投入，并遵循线性生产函数：

每个垄断竞争的中间生产商生产差异化产品，并存在已应用于生产且连续可测度的技术存量At，中间产品的总产出Mt是差异化产出Mtj的CES函数：

其中，ϑ＞1。假设中间产品生产商j使用非熟练劳动力和有效资本Utj K tj并遵循Cobb-Douglas生产函数进行生产：

假设中间产品的价格是完全灵活的，中间产品生产商在每个时期可以随时调整中间产品价格。当中间产品全部作为生产投入用于生产最终产品时，由式（6）～式（9）可以推导出最终产品的总产出Yt的生产函数如下：

上式表明模型的全要素生产率由外生性的TFP冲击θt和内生性的(At)ϑ-1共同构成。因此，模型中的经济变量不仅受外生全要素生产率变化的影响，还受内生全要素生产率变化的影响，内生全要素生产率的变化来源于中间产品种类的扩张所导致的对技术存量采用量的增加，可以用At衡量。

（三）中间生产商

假设中间产品生产商选择资本K tj、资本利用率、非熟练劳动力进行生产，将考虑中间产品组合的相对价格、实际工资wut、中间产品加成定价ςm以最小化生产成本作为生产决策。考虑存在模仿者进入市场的潜在竞争，假设ςm小于最优无约束定价加成ϑ。资本折旧率是关于Utj的凹函数，δ'＞0且δ″＜0。中间生产商成本最小化时K tj、的一阶条件为：

（四）技术研发和技术采用

技术进步和内生全要素生产率增长通过技术研发和技术采用两个过程实现（Comin ＆ Gertler，2006）。首先，技术研发部门通过发明新技术，提高总技术存量Zt，后续中间生产商将新技术应用于生产活动中。在内生TFP 的实现机制中，假设成功研发新技术带来的技术存量的提高不能提高全要素生产率，只有厂商在生产过程中使用这些新技术时，才能实现全要素生产率的提高。因此，模型将技术研发和技术采用划分为先后两个过程，这导致新技术发明成功和现实生产过程中实际采用该技术之间产生时间差。将At表示为已采用的技术存量，是总技术存量Zt的子集，对应TFP中的内生性成分，则Zt-At表示尚未使用的技术存量。如式（10）所示，增加At将有助于提高内生全要素生产率。

对技术研发部门而言，技术研发是内生全要素生产率增长的第一阶段。研发部门雇佣熟练的研发人员Lsrt来创造新技术，在t时期内每位熟练的研发人员可以创造在t+1 时期新技术的数量为φt。φt由下式给定：

其中，表示研发部门熟练劳动力的总水平，Zt为现存的技术总量。χt表示对技术的外生冲击，即在技术研发过程中研发投资对研发效率的外生冲击，服从参数为ρχ和σχ的AR(1)过程。由于研发过程受拥挤效应的影响，假设与研发相关的技术增长弹性ρz＜1，即总体研发活动的增加会降低每个创新者的研发效率。

技术研发部门p的最优决策问题如下：

其中，Jt+1时为还未使用的技术的价值，wst代表单位熟练劳动力的实际工资。

技术研发部门p最优决策一阶条件：

将式（14）代入上式，可得：

式（17）表明额外单位熟练研发劳动力的边际收益现值等于单位熟练研发劳动力的边际成本。若给定的中间产品利润是顺周期的，由未来中间产品利润决定的未采用技术的现值应是顺周期的。该假定和工资黏性假定决定了研发部门雇佣熟练的研发人员和研发投资也是顺周期的。

假设技术随时间变化而过时淘汰的比率为1-τ，即技术的存活率为τ，则Zt+1满足以下条件：

其中，φtLsrt衡量创造的新技术，τZt表示未被淘汰的前期技术。将式（14）代入上式可得：

技术采用的实质是将现存技术Zt转化为可用于生产的技术At的过程。实现技术使用过程需要一段时间，但采用率可以顺周期变化。为避免对每一项可用技术都要跟踪已使用和未使用该技术的公司的比例，假设存在一个有竞争力的技术转化者群体，能够将未使用的技术转化为可用于生产的技术。技术转化者以有竞争力的价格从研发部门购买使用该技术的权利，即为使用技术的价值，并通过雇佣熟练劳动力将购买的技术转化为应用于生产的技术。这一过程需要一段时间，技术转化率受内生变化的影响，转化技术的速度受熟练劳动力数量的影响。假设技术转化者个体特征差异不影响技术转化概率λt，即每个技术转化者的技术转化概率相同。因此，转化者在给定时间t实现技术转化的概率为λt：

其中，Lsat是指在技术采用中雇用的熟练劳动力。假设λ'＞0 且λ″＜0，这意味着使用的速度λt是分配给该部门的熟练劳动力Lsat的递增和凹函数。技术采用的过程意味着技术扩散需要时间，将λt的稳态值表示为λss，则采用新技术之前的平均时间为1/λss。技术采用受总技术存量Zt溢出效应的影响，即技术转化效率会随着技术存量的增加而提高，保证了平衡增长路径的存在。

当技术转化完成，技术转化者将该使用技术的权力出售给中间产品生产商。让表示中间产品企业从生产该产品中获得的利润。技术转化者以具有竞争力的价格出售已转化的技术价值Tt等于生产该商品的利润的现值。

技术转化者最优决策为选择Lsat最大化未使用技术的价值Jt：

式（22）第一项为未采用技术的收益现值，是已使用和未使用技术价值的概率加权总和。熟练劳动力Lsat的一阶条件：

其中，Tt+1-Jt+1是顺周期的，因为未来利润对已使用技术价值Tt的影响大于未使用技术价值Jt。由于工资黏性和顺周期的Lsat，技术转化的概率λt也是顺周期的。

由于λt不受技术转化者个体特征差异的影响，对所有技术转化者进行加总后，根据假设可以得到如下的At递推式：

其中，Zt-At对应未采用技术的存量。应用于生产的技术存量At+1等于当期尚未过时的技术存量之和τλt（Zt-At）及这一时期新转化的技术τAt。

（五）资本生产者

假设新的资本是由竞争性资本生产者利用最终产品生产的，资本生产者将资本品出售给家庭，家庭将资本品出租给中间生产商。将It表示新生产的资本品，γI表示资本品It的增长率表示资本的重置价格，即最终产品转化为新资本的相对价格。假定调整成本函数是递增的凹函数，其中f（1）=f'（1）=0 和f″（1）＞0。因此，托宾Q可以由调整成本函数f表示为：

（六）价格和工资

假设存在价格黏性和工资黏性，公司不能调整其价格的概率为ξp，企业不能调整其工资的概率为ξw。ιp为价格通货膨胀指数化，ιw为工资通货膨胀指数化。家庭提供非熟练劳动力和熟练劳动力，两种类型的劳动力受相同频率的工资调整。通货膨胀为πt，mct为最终产品生产商的边际成本，为稳态对数差分。因此，菲利普斯曲线可以表示为：

其中，εμt表示对最终商品加价的冲击，服从参数为ρμ和σμ的AR(1)过程。

非技术工人的菲利普斯曲线如下：

（七）货币政策

假定货币政策遵循非线性的泰勒规则，央行通过设定名义利率Rnt+1来实施货币政策。

其中，log()遵循参数为ρm和σm的AR(1)过程。为稳态名义利率，为目标通货膨胀率为稳态就业人数，ϕπ、ϕy分别为名义利率对通货膨胀缺口和产出缺口的反应系数。同时对净名义利率施加了零下限约束，即≥1，这也更符合中国名义利率的实际情况。

（八）市场出清

总资源约束条件为：

Gt表示政府消费，由一次性税收作为收入来源并遵循AR(1)过程：

市场出清意味着债券的净供给为零，即Bt=0。

最后，假设熟练劳动力的劳动力市场必须在均衡状态下出清：

四、参数校准及估计

为提高模拟中国经济运行的准确性，参照现有文献和中国经济数据以季度时间为单位对模型参数进行校准和贝叶斯估计。参考仝冰（2017）、卞志村等（2019）和杨兵等的研究（2020）[24-26]，将对以下家庭部门和厂商部门参数进行校准：家庭主管贴现率β=0.99，厂商资本折旧率δ=0.025，厂商资本产出弹性α=0.6，中间产品替代弹性ϑ=10，稳态中间品加成ς=1.18，稳态最终产品加成μt=1.11。对研发部门参数校准参照Anzoategui et al.（2019）的研究，取技术存活率τ=0.98，即技术报废率（1-τ）=0.02；稳态技术使用时滞λss=0.05，即技术转化的平均时间为5年；参考Schmöller ＆ Spitzer（2021）的处理方式，考虑到中国R＆D支出占GDP的比重低于美国，将熟练劳动力的使用弹性校准为ρλ=0.95。参照卞志村等（2019）的方法取稳态政府支出占GDP 比重GY=0.074，稳态产出增长gy取研究期间季度GDP增长率的平均值2.208%。

对余下动态参数采用贝叶斯估计方法，以使参数的取值更为客观合理。首先估计参数的先验分布，参照仝冰（2017）、卞志村等（2019）和Anzoategui et al.（2019）对参数先验分布及其均值和方差的设置，将外生冲击的自回归系数设置为Beta 分布，将其余取值在（0，+∞）的结构参数设置为Gamma 分布，将外生冲击标准差设置为Inv-Gamma 分布（见表1）。考虑数据可得性，选取2002 年一季度至2020 年四季度的产出增长DY、固定资产投资增长DI、通货膨胀率Dπ及名义利率R作为观测变量，以提高模型的可识别性。产出增长DY为以2001 年为基年计算的当季实际GDP 除以总人口后的对数差分；固定资产投资增长DI为当季人均固定资产投资增长除以GDP 平减指数后的对数差分；通货膨胀率Dπ为当季GDP 平减指数的对数差分；名义利率R为当季3 个月期间银行同业拆借加权平均利率的1/4。参数的先验分布及贝叶斯估计结果如表1所示。

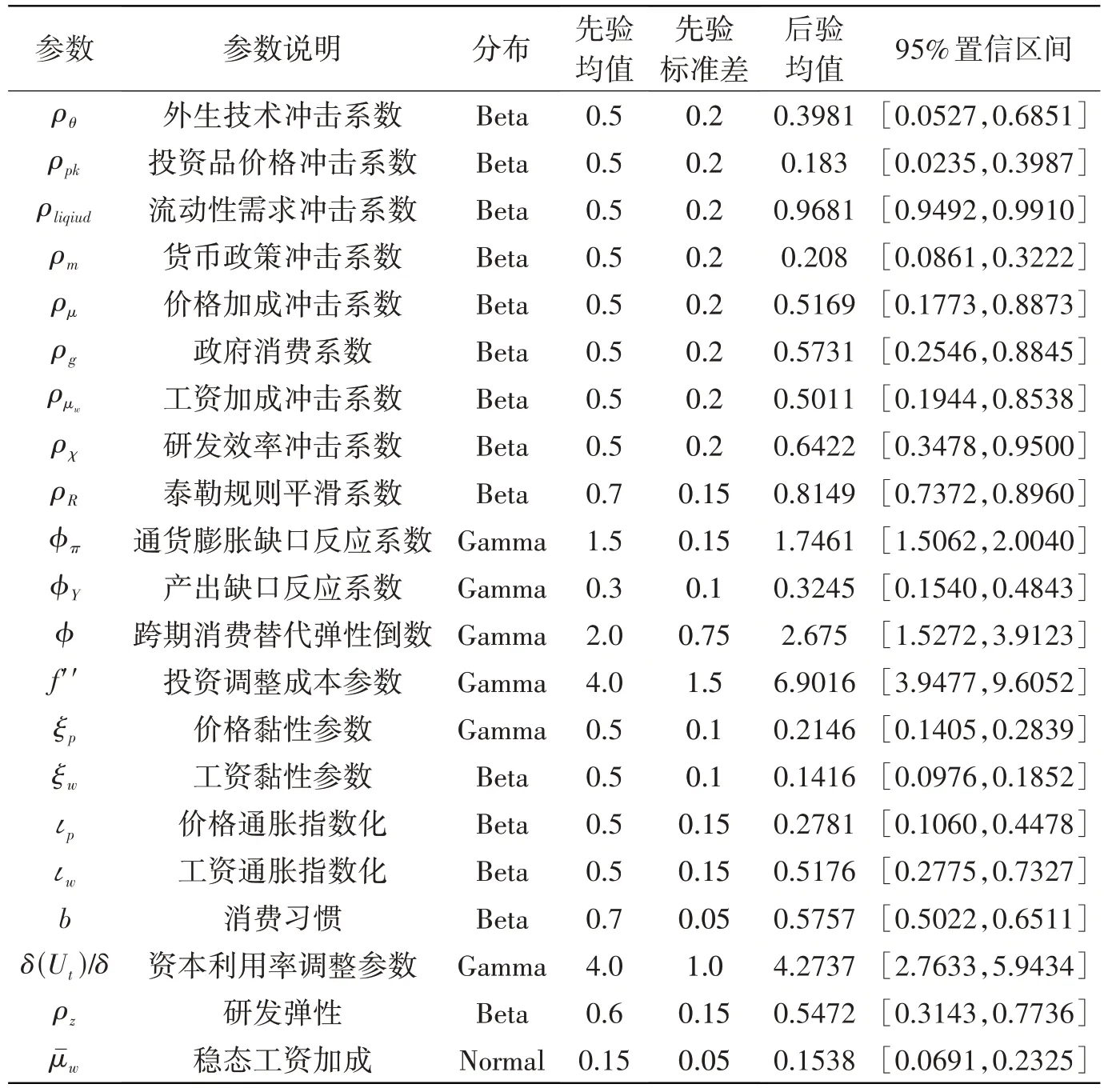
表1 参数贝叶斯估计结果

五、实证分析

（一）方差分解

表2 展示了关键经济变量的方差分解，其中对中国经济变量影响最大的是货币政策冲击，其次是投资品价格冲击和政府消费冲击。货币政策冲击分别占GDP 变化和投资变化的28.82%和35.05%，对消费和研发支出变化的贡献超过50%，对通货膨胀变化的贡献为83.26%。同时，82.71%的内生全要素生产率变化是由货币政策冲击引起的，11.52%是由流动性需求冲击引起的。这说明需求冲击是解释内生全要素生产率变化的重要来源。相较之下，全要素生产率的外生成分即外生TFP冲击对经济变量变化的贡献较小。货币政策冲击、流动性需求冲击和政府消费冲击三种需求冲击解释了48.57%的GDP 增长变化，供给冲击以投资品价格冲击（46.94%）为主，外生TFP 冲击仅占2.77%，表明中国经济高速增长是需求侧驱动和供给侧驱动共同作用的结果。具体而言，货币政策和政府消费是中国GDP 增长的主要需求侧驱动力，而投资品价格则是中国GDP 增长的最重要供给侧驱动力，这与投资、消费、出口驱动经济发展密切相关。较为稳定的货币政策和利率政策、政府购买在消费中占有较大份额、优化营商环境以增加国内外投资等措施都对经济增长作出了重要贡献。流动性需求冲击对中国GDP增长的作用较小，主要由于居民储蓄率普遍较高导致不利的流动性需求冲击对人们提高持有流动性资产需求的影响较小，降低了流动性需求冲击在向消费和投资等领域传递和积累时的影响。

（二）货币政策冲击的脉冲响应

货币政策冲击在短期内提高了名义利率，意味着居民储蓄收益和投资成本增加，直接导致居民消费下降并减少风险资产持有量，使资本投资下降。同时货币政策冲击后总产出的下降导致企业利润下降，从而抑制了企业用于提高生产率的投资，即减少了对研发和技术使用方面的投资。与新凯恩斯模型相比，包含内生全要素生产率的模型表现出更强的经济周期持续性。在内生TFP 模型下，由货币政策冲击引发的产出下降更为显著和持久，消费与投资也表现出该特点。其根本原因是全要素生产率的演化和整体经济运行状况之间存在重要的反馈机制，这种内生机制不存在于新凯恩斯模型。货币政策冲击后，技术使用率小幅上升后持续下降及技术研发支出的大幅下降抑制了全要素生产率并增加其恢复时间，加剧了初期产出的下降并减缓后续产出恢复。由于内生TFP 机制的存在，虽然无风险利率R（名义利率）上升，但对研发和技术使用的投资减少使资本回报率Rk的上行压力更大，导致利差（Rk-R）小幅上升。而在外生TFP 模型中缺乏该机制，使资本回报率Rk的上行压力小于无风险利率上升幅度，利差小幅下降。

（三）全要素生产率的演变及驱动因素

考虑模型中全要素生产率与经济增长的关系，并分析全要素生产率及其内生成分的演变、全要素生产率和劳动生产率之间的关系。对式（10）进行变形可得式（35），其中全要素生产率为(At)ϑ-1θt，内生成分为(At)ϑ-1，外生成分为θt。Yt/Lu，t表示劳动生产率，UtYt/Lu，t表示单位劳动力的有效资本，即有效资本深度。因此，对数线性化后的全要素生产率可以理解为内生TFP 和外生TFP 的加总。劳动生产率可以表示为全要素生产率与有效资本密集度的函数，全要素生产率则为内生TFP 与外生TFP 的乘积。

如图2 所示，模型中的全要素生产率及其内生成分的变化趋势与劳动生产率具有高度相关性，表明全要素生产率的演变和劳动生产率的变化高度一致，全要素生产率尤其是内生TFP 对劳动生产率具有重要影响。劳动生产率和全要素生产率之间的差异源于资本深化程度Kt/Lu，t和资本利用率Ut的波动。TFP 和内生TFP 在研究期间内高度相关，并且全要素生产率的内生成分解释了几乎全部的全要素生产率变动。一般而言，全要素生产率与其内生成分的差异为外生TFP 冲击，即标准技术冲击。外生TFP冲击解释了不能有技术研发和技术使用所内生解释的全要素生产率变动。在研究期间内，TFP 和内生TFP 之间的差异并不明显，即外生TFP对全要素生产率的贡献较小。内生TFP是全要素生产率的决定性因素，外生TFP 冲击则是次要因素。上述分析表明，中国经济增长的一个重要内生驱动因素是内生全要素生产率。正对应方差分解的结果，单纯的外生技术冲击对经济增长的贡献不大。随着中国对基础理论和应用技术研发的投入不断加大，相较于外生技术冲击，由技术部门所贡献的内生全要素生产率的变动更能解释中国经济增长的本质。

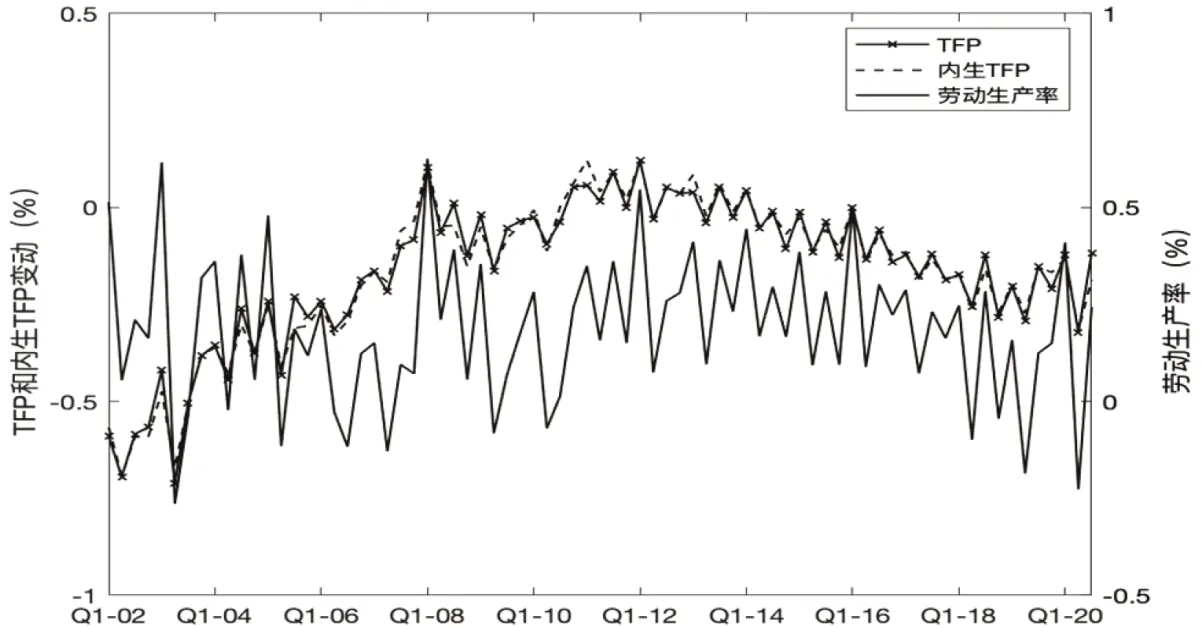
图2 TFP、内生TFP和劳动生产率的演变

（四）内生全要素生产率的决定因素

如方差分解结果所示，对内生全要素生产率变动贡献最大的是货币政策冲击，其解释了82.71%的内生TFP 变动，其次分别是流动性需求冲击和研发效率冲击。因此，货币政策冲击是构成内生全要素生产率变动的最重要驱动因素。图3 展示了内生全要素生产率在研究期间的演变及三种主要冲击的贡献。在研究期内的各期分解中，货币政策冲击和内生全要素生产率的变动呈现出高度相关性，货币政策冲击的贡献显著为正，说明其对内生TFP 变动有决定性作用。从2002 年开始，货币政策冲击对内生全要素生产率的正向贡献不断增大，推动内生全要素生产率不断提高。2007 年起，研发效率冲击对内生全要素生产率的贡献由正转负，并开始逐步下降。但此时，货币政策冲击的正向影响要大于研发效率的负向影响，内生全要素生产率依旧有较高增长。直至2012 年后利率市场化改革的逐步推进，货币政策冲击逐渐趋于平稳，不断扩大的研发效率冲击负向贡献对内生全要素生产率产生了重要影响，导致内生全要素生产率开始逐渐下降。从2018年开始，内生全要素生产率逐渐趋于平稳，主要是因为研发效率的负面效应开始趋于平稳，货币政策的正向效应开始促进内生全要素生产率的增长。但在受2020 年的新冠疫情影响后，内生全要素生产率开始大幅下降。因此，中国内生全要素生产率的增长决定因素是货币政策冲击，2012 年内生全要素生产率下降的主要原因是研发效率的下降及货币政策冲击趋于平稳。

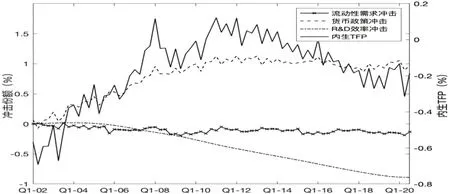
图3 内生TFP及主要冲击贡献

（五）内生全要素生产率与通货膨胀

在分析内生全要素生产率的决定因素及其对经济增长的影响后，尝试在内生全要素生产率模型下探讨中国通货膨胀的动态变化。在式（27）的菲利普斯曲线中，最终产品生产商的边际成本mct受内生全要素生产率的影响，当内生技术创新影响通货膨胀时会导致边际成本mct发生变化。假设最终产品生产商考虑成本最小化，则未对数线性化的边际成本MCt等于中间产品价格pxt与内生全要素生产率(At)ϑ-1的比值，即MCt=pxt/(At)ϑ-1。将式（13）对求积分可得MCt= ςmwutLu，t/((1 - α)Yt)，并将式（10）代入上式并取对数线性化可得边际成本mct为：

因此，具有内生全要素生产率的菲利普斯曲线可以表示为：

上式展示了内生全要素生产率模型中通货膨胀与内生全要素生产率(ϑ- 1)͂和就业͂之间的关系。通货膨胀在新凯恩斯模型和内生全要素生产率模型之间的差异来源于内生全要素生产率(ϑ- 1)͂。在式（28）中，参照参数估计的结果，可以得出kp＞0。因此，通货膨胀和就业之间呈现正相关关系，而内生全要素生产率对通货膨胀产生抑制作用。就业和内生全要素生产率通过影响最终产品厂商的边际成本，进而影响通货膨胀率。不同的是，就业人数的增长会直接增加最终产品企业的边际成本，提高最终产品的交易价格，增加通货膨胀；而内生全要素生产率的提高意味着研发部门的技术创新已经应用于中间产品生产商，提高中间产品生产商的生产效率并降低生产成本，导致中间产品价格下降，进而降低最终生产商将中间产品作为唯一投入进行生产的边际成本，使最终产品的交易价格下降，降低通货膨胀。

方差分解结果说明货币政策冲击是通货膨胀波动最主要的因素，流动性需求冲击次之。如图4所示，货币政策冲击、流动性需求冲击和通货膨胀具有高度相关性。货币政策冲击对通货膨胀的影响为正向，而流动性需求冲击则是拉低通货膨胀的主要原因。2008 年全球金融危机时，不利的流动性需求冲击导致通货膨胀率大幅下跌，但中国利用货币政策和财政政策的组合推动经济复苏，并因此推动了通货膨胀。但随着利率市场化改革的推进，货币政策冲击逐渐趋于平稳，仍是中国通货膨胀最主要的驱动因素。

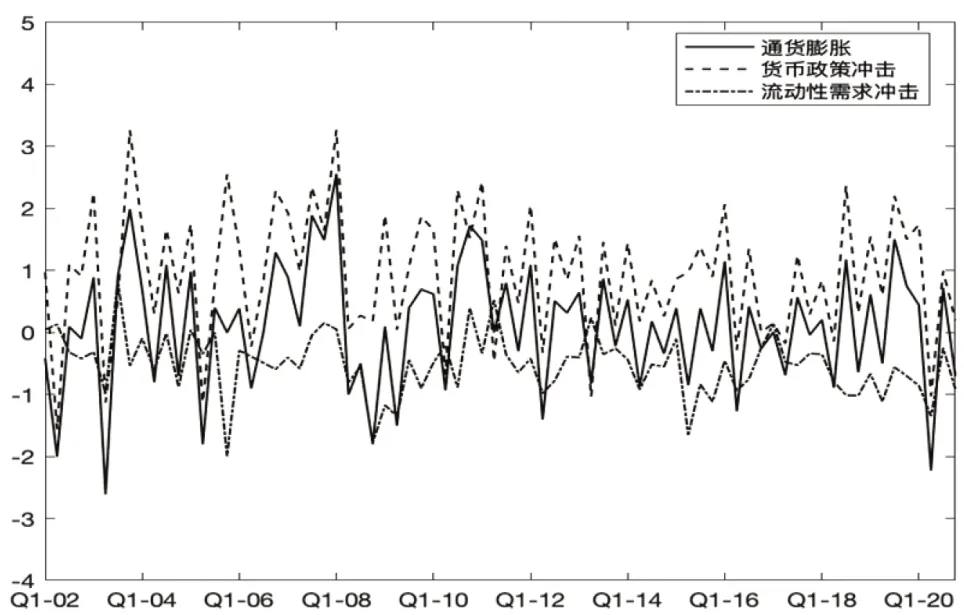
图4 通货膨胀的驱动因素

六、结论与对策建议

作为技术创新促进经济增长的重要途径，全要素生产率的内生化对研究中国经济高质量增长具有关键性作用。首先，通过引入技术创新和技术采用过程，构建具有内生全要素生产率机制的DSGE模型，研究在内生全要素生产率机制下经济波动对产出、消费、投资等主要经济变量的动态效应。其次，探究全要素生产率及其内生成分的主要驱动因素。最后，分析内生全要素生产率与通货膨胀的相互作用及通货膨胀的主要驱动因素。研究发现：第一，在内生TFP机制下，需求侧冲击是主要经济变量波动的主要驱动因素，尤其是货币政策冲击；供给侧的投资品价格冲击对主要经济变量有重要影响，尤其是对产出而言；外生TFP 冲击对主要经济变量的影响并不显著。第二，内生全要素生产率是全要素生产率的决定性因素，外生TFP是次要因素；货币政策冲击是构成内生全要素生产率变动的最重要驱动因素；技术转化率的波动上升是内生全要素生产率增长的主要原因，未来内生全要素生产率增长将更多依靠技术创新带来的技术存量增加。第三，内生全要素生产率对通货膨胀产生抑制作用；内生TFP 机制下菲利普斯曲线的斜率与外生TFP 下的斜率相近，但内生TFP下的斜率更平稳，即内生TFP机制缓解了通货膨胀；货币政策冲击是通货膨胀波动的最主要因素。

为更好利用内生全要素生产率机制促进经济增长，提出以下几点对策建议：一是持续扩大内需，降低投资成本。充分发挥货币政策宏观调控职能，加快利率市场化进程，通过高效协调的货币政策提高国内消费需求。优化营商环境进而吸引国内外投资，降低投资品相对价格，提高资本利用效率，降低投资相对价格冲击对经济的不利影响。二是加强研发部门投入，完善技术创新和科技成果转化体系。技术创新是中国提高产业竞争力和实现高质量发展的重要途径。加大技术创新投入，扩大技术存量，为生产制造提供坚实的技术储备。提高技术创新的转化效率，将技术创新从理论转变成现实生产力，从而提高全要素生产率。三是选择合适的货币政策，保持温和的通货膨胀。由于内生全要素生产率机制的存在，对经济刺激效果更好的货币政策导致的通货膨胀增长较小，政府调控经济时可以选择更为灵活的货币政策，以促进经济增长。