泵站正向进水结构流场特性多目标优化研究

徐存东，胡小萌，王荣荣，王 鑫，田俊姣

(1.浙江水利水电学院，浙江 杭州 310018；2.华北水利水电大学 水利学院，河南 郑州 450046；3.河南大学 土木建筑学院，河南 开封 475004)

1 研究背景

泵站是黄河中上游地区经济社会和农业生产发展中的重要组成部分，受恶劣环境条件限制，引黄灌区泵站初始设计建造标准难以满足规范要求，导致其进水结构内出现脱壁、偏斜等不良流态。同时受黄河水高含沙量影响，泵站进水结构内部泥沙淤积严重，改变了其原有水力条件，对泵站调蓄功能、取水环境、机组性能等造成较大影响，严重时会堵塞水泵吸水口、危及整个泵站的安全运行[1-2]。开展水源含沙提水泵站进水结构过流几何设计参数多目标优化研究，以期改善进水结构流场特性、减轻泥沙淤积、保障良好取水环境，对提高水源含沙提水泵站进水结构流场稳定性、降低泵站运行投入和保障泵站安全高效运行具有重要意义，对相似类型泵站工程更新改造具有指导意义。

近年来，有关学者和技术工程人员在泵站进水池、前池结构优化设计方面进行了一定的研究。其中，Constantinescu等[3]开展了不同后壁距和悬空高度对进水池后壁涡、内附底涡强度及结构的影响研究，得到了进水池流态最佳时的后壁距和悬空高值，并分析了其与后壁涡、内附底涡之间的变化规律；Zarrati等[4]开展进水池表面涡流产生机理及穿孔板消涡效率研究，探明了穿孔板开口与涡流强度的关系；成立等[5]基于单一变量原则，以水头损失和流速分布均匀度为目标函数，得到了合理的后壁距和悬空高取值范围，且研究了不同值对进水池流态的影响；陆林广[6]通过研究后壁距、池宽等参数对进水池流态的影响，并以水泵进口处速度加权平均角和流速分布均匀度为评价指标，对正向进水前池各参数进行了最优设计；孙膑[7]结合模型试验和数值模拟，对高塘湖排涝泵站前池翼墙尺寸、底坡坡度改变后与流态之间的影响关系进行了研究，得到了二者合理取值且发现其值均可改善前池流态。以上研究成果表明，泵站进水结构设计参数的选取对水流流态和水泵水力性能均有不同程度的影响，但在参数优化方面仍存在一些不足，忽略了泵站进水结构中前池和进水池的相互扰动性，未考虑连续取值范围内的最优解，且在进行结构优化设计时未考虑各参数对内部流场特性的共同影响，缺乏多参数的耦合协同优化，优化评价指标与设计参数之间的影响程度还有待明确。

本文以甘肃省景电灌区典型正向进水泵站为研究对象，确定进水结构流场特性评价指标和结构设计参数，利用正交表构建样本数据库。运用PSO-BPNN算法对泵站原型(泥沙淤积前)进水结构流场特性评价指标与设计参数之间的映射关系进行辨识拟合，基于预测输出指标和线性加权法构建目标函数并通过MIGA算法进行全局搜索寻优，实现水源含沙提水泵站原型进水结构流场特性参数耦合协同优化，利用水沙两相流模型对最优设计参数组合进行数值模拟，并对比原设计参数组合分析其优化效果。

2 现场调查与评价指标确定

景电灌区位于我国西北干旱区黄河上游段，属于大Ⅱ型引黄灌区，灌区内建有泵站43座[8]。选取灌区内典型正向进水泵站，其设计流量为6.0 m3/s，设计水位为1604.45 m，共布置机组8台套，其中5#机组设计流量为1.6 m3/s，其余机组设计流量为0.88 m3/s。具体结构形式如图1(a)所示。选取特征观测断面及观测点进行泵站进水结构水沙两相流数值模拟研究，具体位置如图1(b)所示。X轴为横断面，Y轴为纵断面，Z轴为水平断面。P1—P8为吸水管特征断面。Z1断面处于泵站进水结构水深0.2 m处，Z2断面处于泵站进水结构水深0.8 m处，Z3断面处于泵站进水结构水深1.5 m处，Z4断面处于泵站进水结构水深3.0 m处。观测点位于横断面与水平断面的交线上，并沿Y轴方向等间距分布。

2.1 灌区引水含沙特性分析灌区引入黄河水进行灌溉，受黄河泥沙含量变化影响6、7、8月的引沙含量最高，年均、最大含沙量约为30 kg/m3、382 kg/m3，高引沙量使泵站进水前池泥沙淤积现象严重。淤积泥沙呈近似轴对称分布在进水结构中轴线两侧，部分淤积严重区已经影响吸水管正常取水，对典型泵站引水水流和前池淤积泥沙进行粒径取样分析，如表1所列，灌区典型泵站前池内有92.3%的淤积泥沙颗粒粒径在0.075 mm以下，属于极细颗粒沙土。

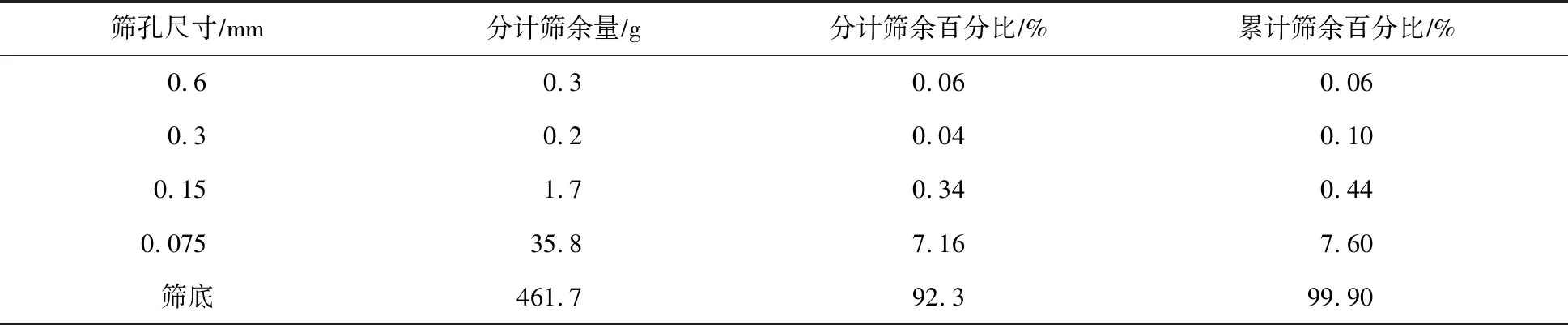
表1 水源含沙颗粒粒径分析表

2.2 流场特性评价指标选取为全面、定量地评价进水结构流场特性，需通过合理评价指标来综合反映泵站进水结构流场特性。固体边界特征对水流内部流场结构的影响直接关系到水流阻力与能量损失的大小，而水头损失凸显出水流流过断面时与边界相互作用而克服水流阻力所做的功，采用进口断面至进水池入口断面的水头损失Hf作为一项评价指标，其计算公式[9]为：

Hf=(Pin-Pout)/ρg

(1)

式中：Hf为水头损失；Pin、Pout分别为进、出口总压强；ρ为水沙两相流密度；g为重力加速度。

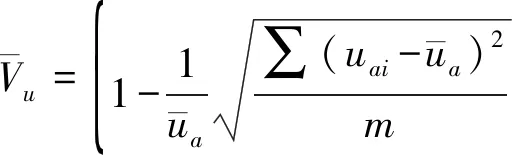
(2)

(3)

(4)

3 流场特性参数优化模型

3.1 流场特性关键参数确定泵站进水结构的水力设计参数主要有扩散角θ、长度LT、总宽度B、底部纵坡i、吸水管的淹没深度hs、悬空高度C、后壁距T等，如图2所示。

选取的典型泵站于1970年代建成，因此其设计参数受当时设计与施工条件影响具有一定的不合理性，参考现行《泵站设计规范》(GB 50265—2010)[11]对各水力参数进行复核并明确其取值范围，因此选取扩散角θ、总宽度B、底部纵坡i、悬空高度C、淹没深度hs、后壁距T等6个因素作为泵站进水结构关键参数，其初始值与具体取值范围如表2所列。

表2 关键参数初始值及取值范围

3.2 样本数据库构建正交设计[12-14]具有搭配均衡、机会均等的特点，正交表是其基本工具，对进水结构流场关键参数给定5个取值水平，如表3所列。忽略参数间相互作用及其他因素影响，采用6因素5水平L25(56)正交表建立初始数据库，由表3设计25组数据，如表4所列。对表4进行扩展，将θ和T调整为50.00°、42.00°、35.00°、32.00°、25.00°和0.60、0.75、0.90、1.10、1.15 m，形成2个新的L25(56)正交表，结合表4共计75组样本数据，由此构成PSO-BPNN训练数据库。

表3 数值模拟试验因素水平表

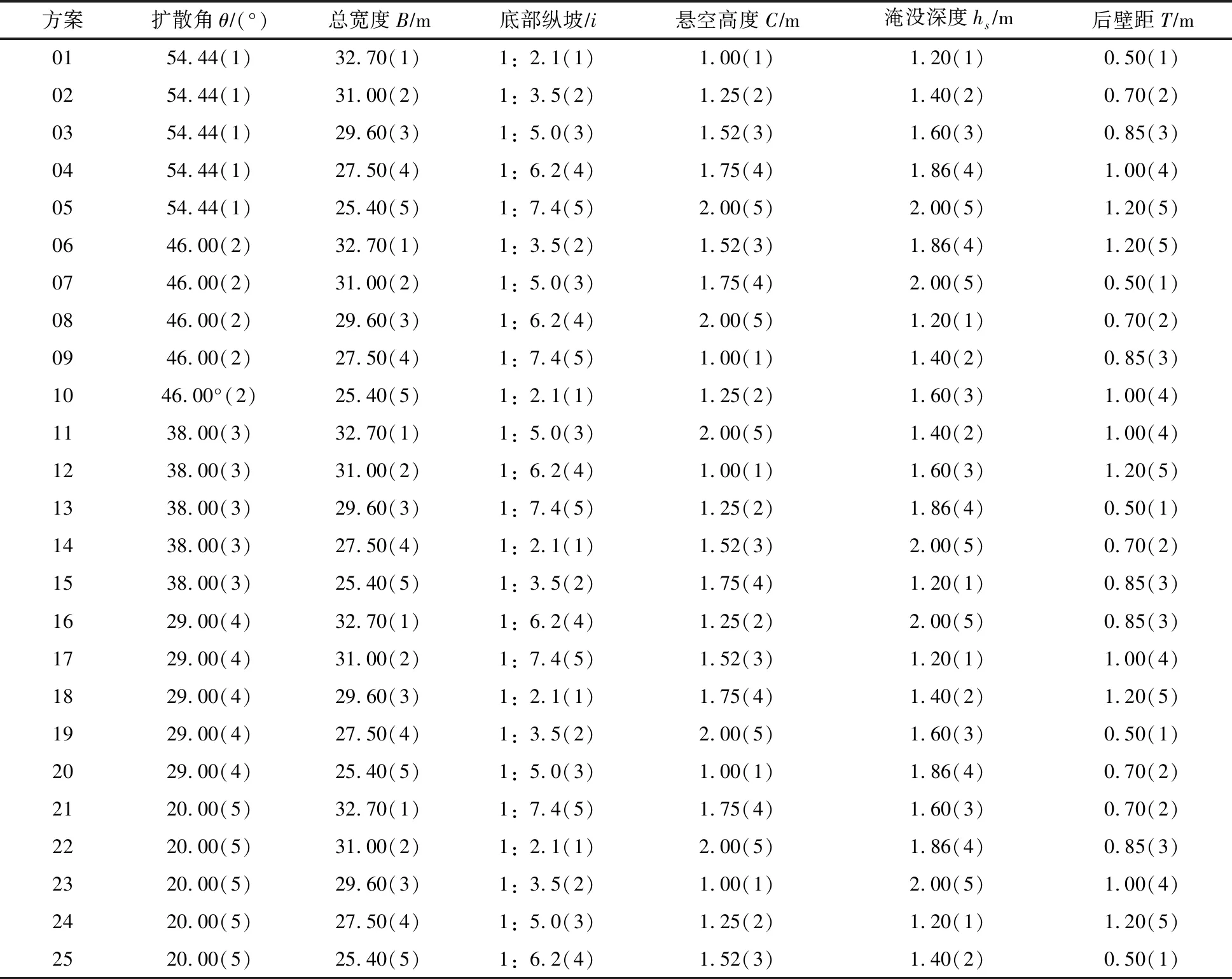
表4 数值模拟正交方案试验因素表

为实现数据集的无量纲化，采用极差法对样本数据进行归一化处理，然后进行网格训练：

(5)

式中：x′di为归一化后的样本数据；xdi为原始样本数据；xmax、xmin为xdi中的最大值、最小值。

3.3 PSO-BPNN-MIGA耦合优化模型

预测仿真智能算法(PSO-BPNN)[15-16]利用粒子群算法[17](PSO)优化BP神经网络[18-19]的权值与阈值来提升对信息间非线性映射关系的预测能力，算法流程如图3所示。多岛遗传算法(MIGA)[20-22]以遗传算法(GA)为基础，将种群分割为多个相互独立的“岛”并进行GA优化求解，同时各“岛”间个体定期迁移互换保证了群体多样性，其有效提升了计算能力、运行速度和全局搜索能力，算法流程如图4所示。

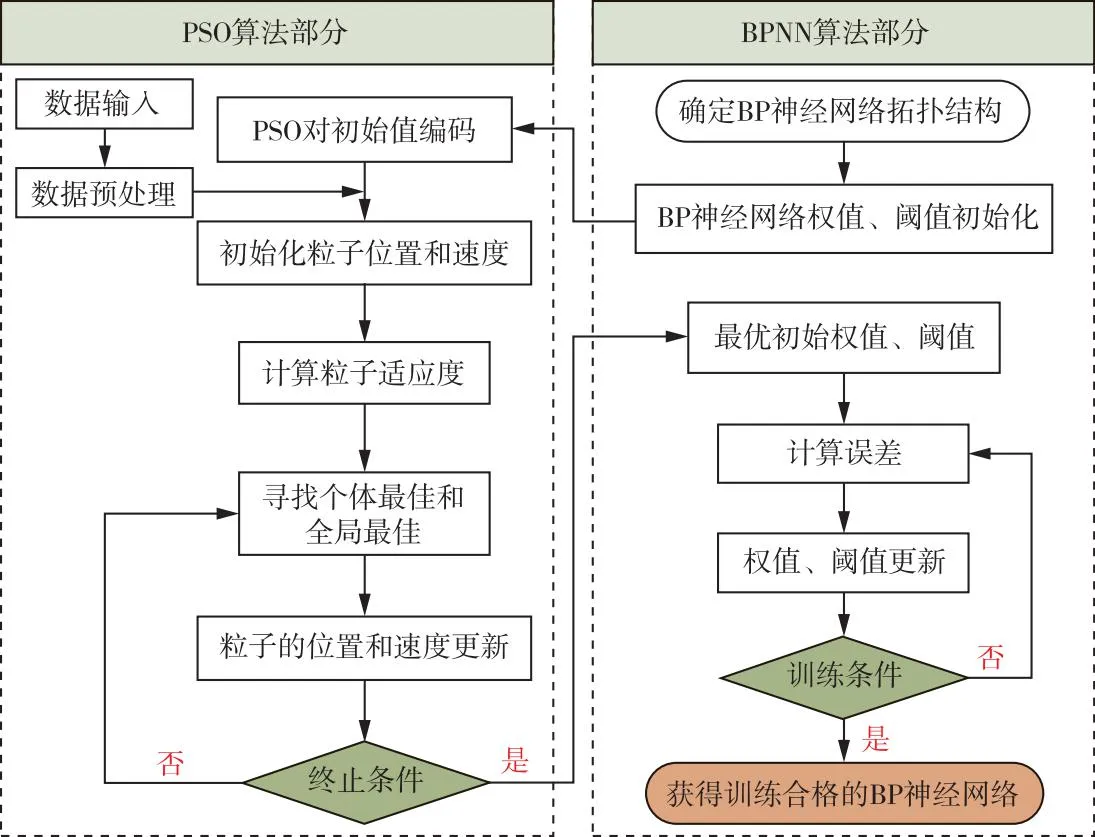
图3 PSO-BPNN算法流程图

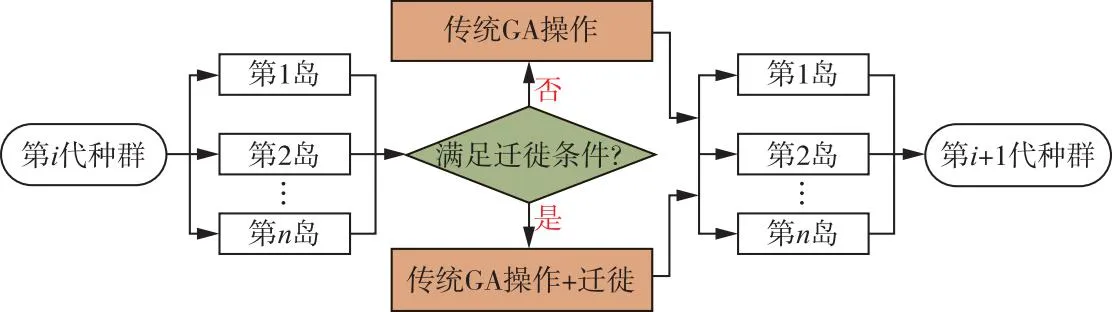
图4 MIGA算法流程图

由于流场特性评价指标之间具有明显的非一致性且进水结构设计参数对其流场特性的影响存在复杂非线性关系，需要对流场特性评价指标与结构设计参数之间的非线性映射关系进行准确辨识。基于PSO-BPNN和MIGA构建多参数多目标耦合优化模型PSO-BPNN-MIGA，利用PSO-BPNN预测辨识和拟合泵站原型进水结构流场特性评价指标与设计参数间的映射关系，对预测输出的指标利用线性加权法构建目标函数，最后通过MIGA对目标函数进行全局搜索寻优，实现泵站原型进水结构流场特性参数多目标优化。耦合优化模型运算流程如图5所示，由相关研究成果[23-24]和经验得到模型参数配置，如表5所列。

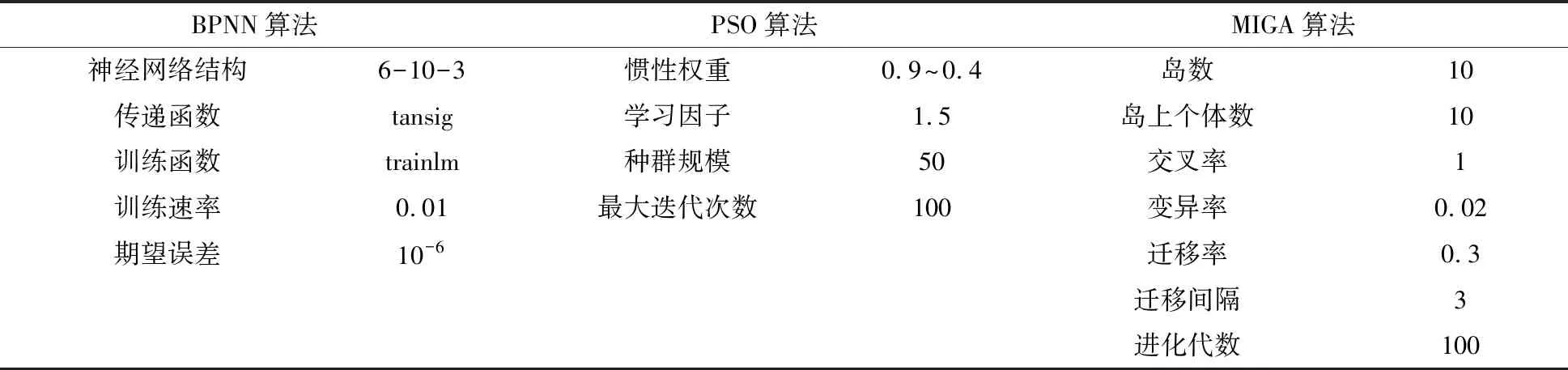
表5 PSO-BPNN-MIGA耦合优化模型参数配置

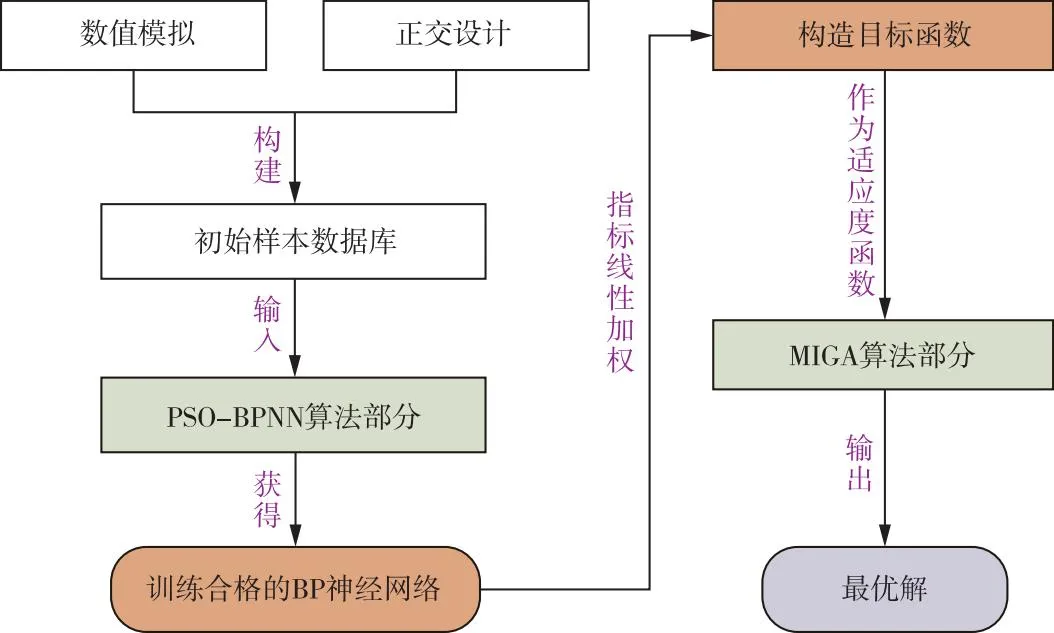
图5 PSO-BPNN-MIGA耦合优化模型流程图

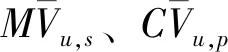
(6)

4 优化模型应用与分析

4.1 数值模拟结果分析Realizablek-ε湍流模型可更精确地模拟射流、旋转流、边界层流、分离流以及管内流动等问题，实现了在雷诺应力上和真实的湍流保持高度一致，而Mixture多相流模型求解的是流体混合物动量方程，并采用相对速度描述离散相。因此，采用Realizablek-ε湍流模型耦合考虑相间滑移的Mixture多相流模型[8，25-28]对表4正交设计25组方案进行模拟，图6列出模拟结果中具有代表性的6组Z3断面流速矢量图。由模拟结果可知，各方案数值模拟结果因泵站进水结构设计参数的变化而各不相同。其中，方案01至方案12主要表现为进水结构流场分布具有明显的对称性，主流效应明显，两侧回流区范围大，主流方向与中间5#机组吸水管进水方向一致，与其他机组均存在一定的夹角；方案13至方案21的主流严重偏向进水结构某一侧，主要向左侧偏斜，可能是受泵站进水结构水下容积增加以及泵站机组非对称布置的影响，所有机组吸水管进水方向与水流方向均存在一定的夹角；方案22至方案25进水结构流场分布趋于均匀，水流进入进水结构后未立即出现脱壁，主流范围明显增加，进水结构两侧存在范围相对较小的窄长带状回流区，流场分布情况和吸水管进水条件相对优于方案01至方案21，这一结论在一定意义上支持了“扩散角越小，水流扩散效果越好”的说法。

图6 部分正交设计方案Z3断面流速矢量图

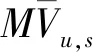
采用极差法[29]分析影响泵站进水结构流场特性指标的主次因素，计算因素各水平指标值的极差大小直接反映了相应因素对指标影响作用的大小，即极差大的因素，其不同水平对指标造成的差别也大，一般为主要因素，反之极差小的因素一般为次要因素。泵站进水结构正交设计数值模拟方案各评价指标极差分析结果见表6。

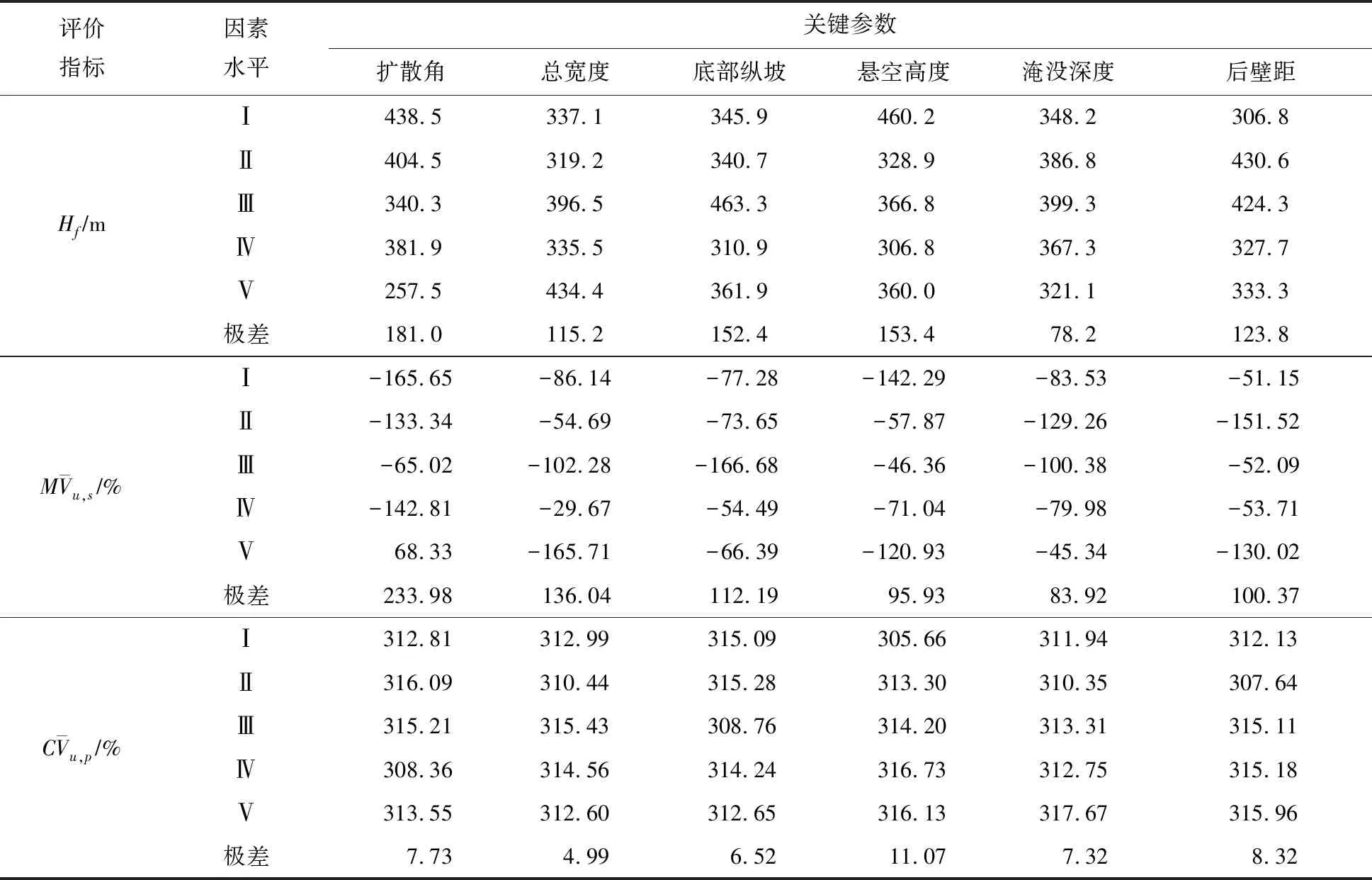
表6 评价指标极差分析表

4.2 优化模型应用

4.2.1 预测精度分析 基于样本数据库进行PSO-BPNN网络训练，随机选取65组作为训练集，剩余样本作为测试集，则训练集(Train)、验证集(Validation)、测试集(Test)均方根误差曲线及其回归能力如图7、图8所示。

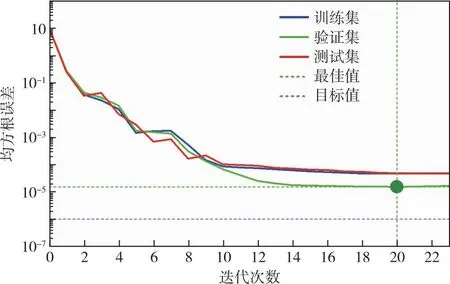
图7 PSO-BPNN模型的均方根误差

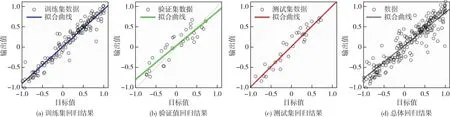
图8 PSO-BPNN模型拟合曲线

图7可知，当训练至第20代时，Validation的均方根误差达到最佳值1.51×10-5，Train、Test的均方根误差均达到10-4以下；由图8得到，目标值、输出值拟合精度R均在0.9以上，表明PSO-BPNN模型具有较高的预测精度，能够较好辨识泵站原型进水结构流场特性评价指标与设计参数间的映射关系。

4.2.2 最优参数确定 运用PSO-BPNN-MIGA耦合优化模型求解泵站原型进水结构参数，将得到的最优设计参数组合(OPT)、评价指标值组合与原设计参数组合方案ORG进行对比，如表7所列。

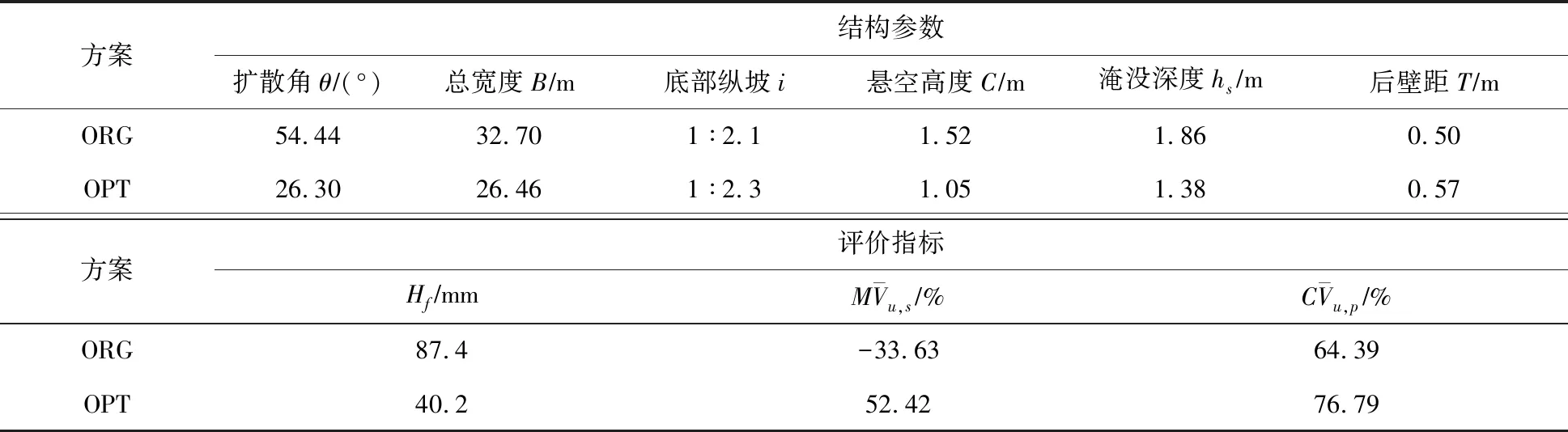
表7 泵站进水结构多参数多目标优化结果对比

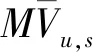
4.2.3 PSO-BPNN-MIGA模型可靠性分析 对最优参数方案(OPT)几何建模、网格划分，并运用Realizablek-ε湍流模型耦合考虑相间滑移的Mixture多相流模型进行数值模拟，将模拟计算值与PSO-BPNN-MIGA模型预测值进行对比。

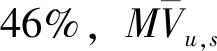
表8 OPT方案评价指标预测值与计算值偏差分析

4.3 最优参数方案(OPT)数值模拟

4.3.1 流场特性优化效果分析 利用Realizablek-ε湍流模型耦合考虑相间滑移的Mixture多相流模型对OPT方案下泵站原型进水结构断面流速分布进行数值模拟，如图9—11所示，分析PSO-BPNN-MIGA对进水结构流场特性的优化结果。

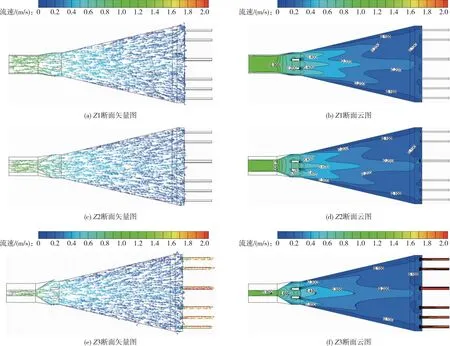
图9 OPT方案断面流速分布

由图9可看出，OPT方案下进水结构水流流速分布与结构形态相同且扩散效果较好，能够流畅进入各吸水管，在进水结构内无明显旋涡回流现象，低流速水流主要分布在两侧边壁带状区域；由图10可知，优化方案进水结构内流线分布均匀，部分水流仅在进水结构末端受后壁限制发生平面、垂向扩散，部分流线出现变向现象且沿水深方向流速减小。

图10 OPT方案进水结构纵断面流速分布

由图11分析可得，OPT方案下各机组吸水管特征断面流速分布均匀度在76.14%～80.70%之间，管壁过度区、高速区域流速梯度分布较为均匀，断面轴向流速中心基本处于管道断面中心且无明显偏斜。以上分析表明，PSO-BPNN-MIGA模型在泵站原型进水结构流场特性参数多目标优化中可取到良好效果。

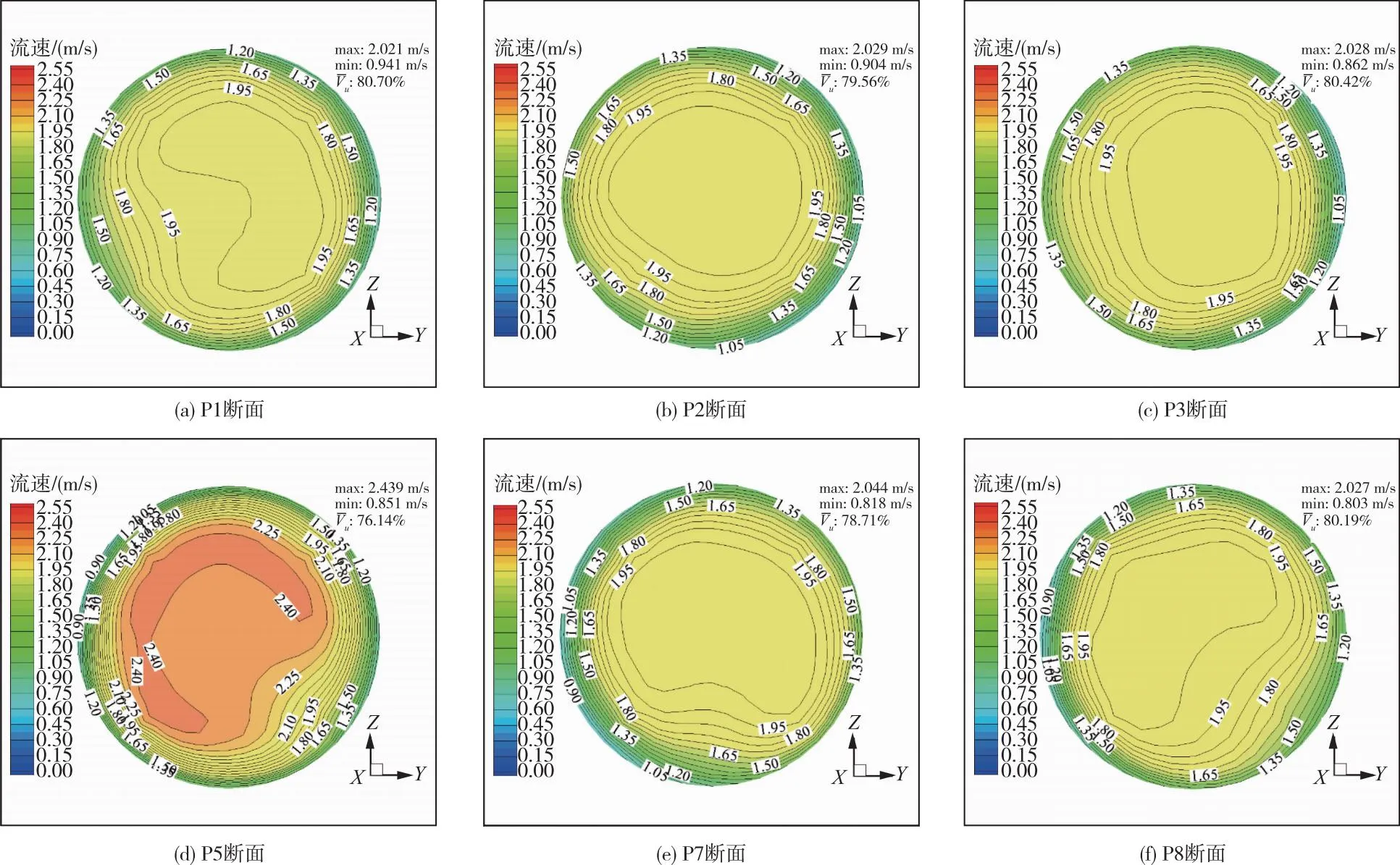
图11 OPT方案吸水管特征断面轴向流速云图

4.3.2 泥沙淤积优化效果分析 对OPT方案下进水结构近底泥沙体积分数分布运用水沙两相流数值模型进行模拟，如图12所示，发现进水结构内无明显泥沙淤积现象，近底泥沙体积分数最大为0.022 83且多数区域低于0.013，由于水流挟沙能力小且流速低，因此仅在流速低于0.100 m/s的区域和进水池局部区域泥沙体积分数有细微升高。通过耦合优化模型得到的优化方案在一定程度上能够改善减少泥沙淤积，但不能完全解决泥沙淤积难题，由于泵站引水含沙量本底较高，因此只能通过结构、运行优化和附加工程措施等方式最大化缓解水源含沙提水泵站进水结构泥沙淤积问题。

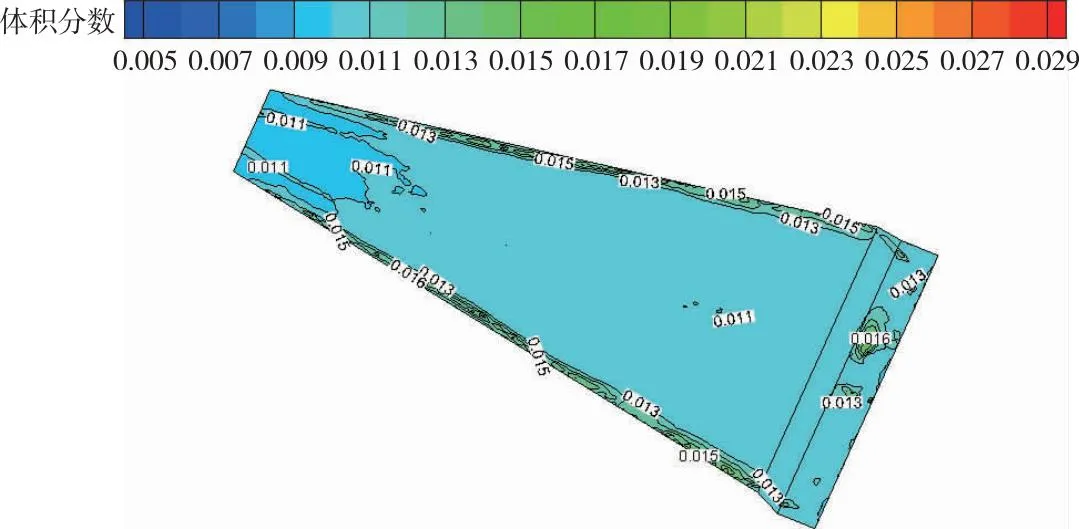
图12 OPT方案近底泥沙体积分数分布

5 结论

(1)通过PSO-BPNN-MIGA耦合优化模型得到最优方案OPT，其设计参数组合为：扩散角θ=26.30°、总宽度B=26.46 m、底部纵坡i=1∶2.3、悬空高度C=1.05 m、淹没深度hs=1.38 m、后壁距T=0.57 m；各评价指标模型预测值与模拟计算值偏差率均在10.00%以内，表明PSO-BPNN-MIGA耦合优化模型在泵站原型进水结构协调优化中可靠性较好，可实现各设计参数区间内的连续全局寻优。

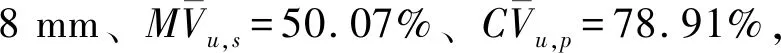
(3)PSO-BPNN-MIGA耦合优化模型有机融合了PSO、BPNN、MIGA三种智能算法的主要功能与优点，有效解决了泵站原型进水结构流场特性多参数多目标优化问题中的参数区间内无缝式精确寻优，同时结合正交设计和水沙两相流数值模拟高效构建了初始样本数据库，进一步提升了耦合优化模型的稳健性和求解效率。

(4)根据数值模拟结果所取的各指标权重系数使得泵站进水结构体型得到了优化，但指标权重系数在取值过程中存在人工经验性影响，所得结果仍可能不是最优；同时，样本数据由三维数值模拟所得，计算历时相对较长、数据量相对较少，在未来的研究中，需更合理的确定各指标权重系数和丰富研究所需的样本数据集，以进一步优化泵站进水结构流场特性。