水击补气式压力罐及水力瞬变仿真

2024-03-18杨开林

水利学报 2024年2期

杨开林

(流域水循环模拟与调控国家重点实验室中国水利水电科学研究院，北京 100038)

1 研究背景

空气阀是管道输水工程中必不可少的防止水击破坏的调压设备，一般间隔500～1000 m距离就会设置。此外，长距离输水管道一般采用地下埋设的方式，当管道直径较大时，需要在间隔1～3 km距离设置检修孔，其内径一般为0.8～0.9 m，以便进人检查输水管是否存在严重泄漏。在一些埋深较大的城市输水管线，检修孔高度或顶盖与输水管顶部的距离hori可达3～5 m以上。为了节省空间，空气阀和检修孔常常共用一个地下室。同时，为了不停水检修空气阀的需要，每个空气阀都配套相同规格的手动检修蝶阀。由此产生了两种主要的空气阀安装方式：(1)空气阀-检修阀-连接管垂直安装在输水管顶部；(2)空气阀-检修阀-连接弯管安装在检修孔侧壁，如图1(a)所示。为便于安装和拆卸检修孔顶盖，连接弯管与顶盖之间需要一定距离，这使空气阀进气后的部分气体会存留在检修孔上部，产生气垫式压力罐的水击防护作用，如图1(b)所示。

图1 空气阀-检修孔装置工作原理

为了兼顾管道充水和泵站事故断电水击危害防护的需要，规范要求采用计算仿真的方法确定空气阀的位置、类型和孔径。目前一般采用著名瞬变流专家Wylie和Streeter[1]的数学模型求解空气阀的水力瞬变[2-9]，该数学模型成立的基本假设包括：(1)管内气体的变化遵守等温规律；(2)液体表面的高度基本不变，即忽略空气阀及其配套检修阀和连接管高度的影响。

虽然Wylie和Streeter的空气阀水力瞬变数学模型在工程计算中广泛采用，包括现有商用软件，但是该模型基本假设1和2在理论和实用方面均存在问题。为此，杨开林[10]基于等熵流动的气动力学理论，建立了管内气温与气压的函数关系，从而导出新的空气阀进排气基本方程，然后，考虑空气阀安装方式1条件下空气阀-检修阀-连接管结构尺寸的作用，提出了新的空气阀水力瞬变数学模型及其求解算法。不过，对于空气阀安装方式2条件下的水力瞬变过程，目前尚未引起关注，缺乏基本的理论研究。

另一方面，在现有的空气阀安装设计中一般要求将通过空气阀进入输水管的气体完全排出，原因是担心气体长期滞留在管道中产生不可预测的危险水击现象，诸如液柱弥合冲击水压破坏管道。不过，从目前大量管道工程空气阀安装方式2的长期运行实践来看，气体存留在检修孔上部并未给运行带来明显不利影响，即使这些气体最终会完全溶解于水。这就给出一个启示，当按照常规空气阀安装方式1不能满足水击防护要求时，可以利用空气阀与其它调压方法结合形成新的调压设施，例如真空破坏阀或空气阀与压力罐结合形成水击补气式压力罐。

本文主要目的是，首先提出两种水击补气式压力罐的设计方法，然后分析其水力瞬变的特点并建立数学模型，最后通过工程算例计算比较分别设置空气阀、空气阀调压室[11]、水击补气式压力罐的防护效果。

2 水击补气式压力罐

压力罐是泵站加压输水系统水击危害防护的常用安全设备。与单向调压室相比，压力罐不仅能够防负压，而且能够消减最大水击压力。不过，常规的压力罐需要配套专用空压机和自动监测监控装置，而气囊式压力罐投资较高，需要定期更换气囊。鉴于此，可参考空气阀-检修孔装置，发展新型的水击补气式压力罐装置。水击自补气压力罐可划分为两类：真空破坏阀补气式压力罐，空气阀补气式压力罐，如图2所示。

图2 水击补气式压力罐

真空破坏阀宜布置在压力罐顶部，其特点是只容许空气进入压力罐，不容许气体排出压力罐。空气阀连接管需布置在压力罐侧壁且向上倾斜，其特点是，当罐内水位Hs低于连接管高程Zct时，容许气体流入和排出压力罐，而当Hs>Zct时，压力罐内的气体不会被空气阀排出，优点是可以兼顾输水管充水、排水和事故断电水击防护要求。显然，空气阀-检修孔装置可视为空气阀补气式压力罐的一个特例。

空气阀补气式压力罐的水力瞬变可划分为四个阶段：阶段1，压力罐顶部没有气体且压力罐水位Hc≡Zmt保持不变，空气阀进气和排气，空气阀-检修阀-连接管水位Hs在高程Zct和Zat之间变化；阶段2，水位Hc≡Zct不变，空气阀进气，并上浮到压力罐水面以上，使得水位Hc从高程Zmt逐渐下降到Zct；阶段3，空气阀进气和排气，水位Hc=HsZct的现象，此时，气体把水体分隔为两部分，一小部分在空气阀-检修阀-连接管中，其余在压力罐中。需要说明的是，在一些情况下，水力瞬变过程不会遵循阶段1、2、3、4的顺序进行，例如，在阶段2，空气阀因输水管水压重新上升开始排气时，水力瞬变过程就会跳过阶段3，直接进入阶段4。

当初始工况压力罐顶部存在气体时，空气阀补气式压力罐的水力瞬变将从阶段4开始，然后在阶段2—4之间变化。对于图2(a)所示真空破坏阀补气式压力罐，其水力过渡过程只有阶段1和3。由于水力瞬变持续的时间一般很短，在计算分析时可以不考虑气体的释放和溶解。

3 数学模型

为使问题简化，首先假定：(1)气体为理想(完全)气体且等熵的流进流出空气阀；(2)进入输水管的空气留在它可以排出的检修孔附近，以便用常规水击特征线方法求解输水管道水力瞬变；(3)进入压力罐(或检修孔)的空气不会被水流带走，而是上浮到压力罐水面以上。

由于真空破坏阀补气式压力罐的水力瞬变过程只是空气阀补气式压力罐的一部分，下面以后者为主要研究对象。

3.1 空气阀的进排气数学模型参考文献[10]，空气阀的进排气数学模型如下：

(1)空气以亚声速进气

(1)

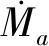
(2)空气以临界声速进气

(2)

(3)空气以亚声速排气

(3)

式中：Cout为排气流量系数；Aout为排气孔流通面积，m2；prc，out=1/prc，in为排气临界压比。

(4)空气以临界声速排气

美国水行业协会标准AWWA M51指出，当排气压比等于或大于临界声速排气的压比(pr≥prc，out)时，空气将以声速流动，即便压强差持续增大。令式(3)中pr=prc，out，可得空气以临界声速排气的质量流量

(4)

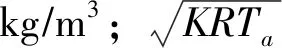
5)等熵条件下的气体状态方程

(5)

式中：-V为气体体积，m3；Ma为气体质量，kg。

3.2 空气阀补气式压力罐水力瞬变数学模型参考图2(b)，空气阀连接管进口连续性方程是

Qa=Qs-Qc

(6)

式中：Qa为空气阀或连接管的流量，m3/s；Qs为压力罐底部阻抗孔的流量，m3/s；Qc为压力罐高程Zct上部的流量，m3/s。

压力罐底部节点的连续性方程为

Qs=QT-Q

(7)

式中：QT为流入节点的输水管流量，m3/s；Q为流出节点的输水管流量，m3/s。

根据水击特征线相容性[1-2]可得

C+：QT=CP/BP-HP/BP

(8)

C-：Q=-CM/BM+HP/BM

(9)

在时刻t参数BP、BM、CP、CM是已知量，由输水管道系统水力瞬变计算确定。

把式(8)(9)代入式(7)得

Qs=C1-C2HP

(10)

式中：

(11)

3.2.1 空气阀-检修阀-连接管-压力罐水位、气体体积、流量、气压的函数关系

(12)

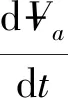
(13)

式中：t为时间，s；Hs为空气阀-检修阀-连接管-压力罐水位，m；As为对应Hs的过流截面积，m2；-Va为Hs上部气体体积，m3；Z为输水管顶高程，m；Zat为空气阀进口高程，m。

对式(12)(13)积分并取二阶近似得

Hs=C31+C41Qa，Z≤Hs≤Zat

(14)

-Va=-Va0-0.5Δt(Qa+Qa0)

(15)

式中：下标“0”表示时刻t0；Δt=t-t0；

(16)

式中：Aa为空气阀-检修阀-连接管截面积，m2；Ac为压力罐截面积，m2。C31=Z和C41=0相当于取Hs=Z，即假设进入输水管的空气留在它可以排出的压力罐附近。

当不考虑水体惯性力和沿程水头损失的影响，则气体绝对压强p与输水管顶测压管水头HP的关系是

Hapr=HP+Ha-Hs-C5|Qs|Qs-C5a|Qa|Qa

(17)

式中：pr=p/pa为空气阀压比；pa为绝对大气压强，Pa；Ha=pa/γ为大气压头，m；γ为水的重度，一般取9800 N/m2；C5为压力罐阻抗孔的阻抗系数；C5a为连接管出口的阻抗系数；

把式(10)(14)代入式(17)，消去HP和Hs可近似得

Hapr=C1/C2-Qs/C2+Ha-C31-C41Qa-2C5|Qs0|Qs+C5|Qs0|Qs0-2C5a|Qa0|Qa+C5a|Qa0|Qa0

(18)

3.2.2 压力罐水位、气体体积、气压与流量的函数关系

(19)

(20)

式中：Hc为压力罐水位，m；-Vc为压力罐气体体积，m3。

对式(19)(20)积分并取二阶近似得

Hc=C32+C42Qc，Z≤Hc≤Zmt

(21)

-Vc=-Vc0-0.5Δt(Qc+Qc0)

(22)

式中：

(23)

式中C32=Z和C42=0相当于取Hc=Z，即假设进入输水管的空气留在它可以排出的压力罐附近。

当不考虑压力罐水体惯性力、沿程水头损失的影响，则压力罐气体绝对压强pc与输水管顶测压管水头HP的关系是

Hapcr=HP+Ha-Hc-C5|Qs|Qs

(24)

式中pcr=pc/pa为压力罐内气体压比。

把式(10)(21)代入式(24)，消去HP和Hc可得

Hapcr=C1/C2-Qs/C2+Ha-C32-C42Qc-2C5|Qs0|Qs+C5|Qs0|Qs0

(25)

3.3 空气阀补气式压力罐的水力瞬变的数值求解假设初始时刻压力罐内没有气体，下面将根据第2节所述空气阀补气式压力罐水力瞬变的四个阶段，研究各阶段的数值求解方法。

阶段1：压力罐顶部没有气体且压力罐水位Hc≡Zmt保持不变，空气阀进气和排气，空气阀-检修阀-连接管水位Zct≤Hs≤Zat。这时，Qc≡0而Qa≡Qs。当HP=C1/C20时，空气阀排气。

把Qa≡Qs代入式(18)可得

Qs=C6-C7pr

(26)

其中：

(27)

式中：ω为压力罐阻抗孔截面积，m2；ζ和ζa分别为阻抗孔和连接管出口的局部阻力系数，为突扩或突缩和90°转弯的组合。C5a右边第二项为水位Hs变化在空气阀-检修阀-连接管中产生的附加阻抗系数。

把式(26)代入式(15)得

-Va=C8+C9pr

(28)

其中：

C8=-Va0-0.5Δt(C6+Qs0)，C9=0.5ΔtC7

(29)

气体等熵流动的气体状态方程式可描述为

(30)

把式(28)气体体积-Va代入式(30)可得

(31)

在时刻t0参数已知的情况下，式(31)只有压比pr是未知量函数，可用参考文献[10]方法求解，然后由式(26)(28)(14)(10)(8)(9)计算得时刻t的Qs、-Va、Hs、HP、QT、Q。但是，当Hs≥Zat，即空气阀完全关闭，则令Hs=Zat、Qs=0、a=0、Ma=0，然后由式(10)(8)(9)确定HP、QT、Q。

阶段2：空气阀进气，Hs≡Zct和Zct≤Hc≤Zmt。

进入压力罐的气体，一部分可能被水流挟带进入输水管，另一部分将上浮到压力罐顶部使水位Hc下降到Zct。挟带进入输水管气体与上浮到压力罐水面以上气体的比例与压力罐流速V=Qs/Ac和压力罐高度h=Zct-Z有关。V越大、h越小，进入输水管的气体越多，但是具体多少，目前知之甚少。为了使问题简化，下面假设进入压力罐的空气不会被水流带走，而是上浮到压力罐水面以上。

当

(32)

则可采用阶段1数学模型计算确定pr、Qs、-Va、HP、QT、Q，直到下式

-Va≥-Va1+-Vc1

(33)

成立为止，即压力罐高程Zct以上空间全部被气体占据为止。式(33)右边-Va1和-Vc1分别为空气阀-检修阀-连接管和压力罐上部的气体容积。

在阶段2，压力罐顶部绝对气体压强。

pc/γ=p/γ-(Hc-Zct)

(34)

上式表明在阶段2期间，压力罐气压pc小于空气阀气压p，这意味着压力罐顶部相对气压小于大气压。

不过，如果在计算的过程中pr≥1，即空气阀开始排气，则水力瞬变跳过阶段3，直接进入阶段4。

阶段3：空气阀进排气，Hs=Hc≤Zct。

在阶段3，在气体等熵流动条件下，压力罐气压与空气阀-检修阀-连接管气压相同，即pc=p，当令

(35)

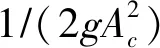
阶段4：压力罐上部存在气体，Hs>Zct。

(1)气体压比与体积的关系。压力罐气体压比与气体体积的关系是

(36)

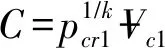
空气阀-检修阀-连接管气体压比与气体体积的关系是

(37)

设阶段3末了时刻气体质量为Ma30，而压力罐上部和空气阀-检修阀-连接管气体质量分别为Mac0和Ma0，则存在下述关系

Ma30=Mac0+Ma0，Mac0/Ma0=-Vc1/-Va1

求解可得

Ma0=Ma30/(1+-Vc1/-Va1) ，Mac0=Ma30(-Vc1/-Va1)/(1+-Vc1/-Va1)

(38)

式中Mac0和Ma0也分别为阶段4初始时刻t0压力罐和空气阀-检修阀-连接管内的气体质量，kg。

(2)压力罐和空气阀流量与气体压比的关系。对于空气阀-检修阀-连接管，把式(6)代入式(18)可得Qs、Qc与pr的线性代数方程

a11Qs+a12Qc=d1-pr，Hc≥Zct，Hs≥Zct

(39)

其中：

(40)

对于压力罐，由式(25)可得Qs、Qc与pcr的线性代数方程

a21Qs+a22Qc=d2-pcr

(41)

其中：

a21=(1/C2+2C5|Qs0|)/Ha，a22=C42/Ha，d2=(C1/C2+Ha-C32+C5|Qs0|Qs0)/Ha

(42)

当HcZct和不考虑压力罐水流惯性和沿程水头损失时，可得

Hapcr+Zct=Hapr+Hs+C5a|Qa|Qa，HcZct

(43)

把式(6)(14)(41)代入式(43)可得

Ha(d2-a21Qs-a22Qc)+Zct=Hapr+C31+(C41+2C5a|Qs0-Qc0|)(Qs-Qc)-C5a|Qs0-Qc0|(Qs0-Qc0)

整理得

a11Qs+a12Qc=d1-pr，HcZct

(44)

其中：

(45)

采用克莱姆法则联立求解线性方程组(39)(41)或者(41)(44)得

(46)

(47)

其中：

Δ=a11a22-a12a21，ΔQs=(d1-pr)a22-(d2-pcr)a12，ΔQc=(d2-pcr)a11-(d1-pr)a21

(48)

(3)-Va、-Vc与压比pr、pcr的关系。把式(46)(47)代入式(15)消去Qs和Qc可得

-Va=d3+a31pr+a32prc

(49)

其中：

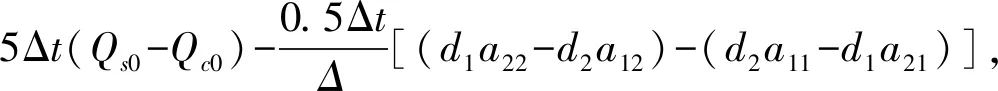
(50)

把式(47)代入式(22)消去Qc可得

-Vc=d4+a41pr+a42prc

(51)

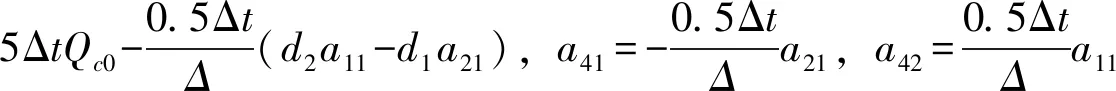
(52)

(4)压比pr、pcr数值求解。把式(49)(51)分别代入式(37)(36)得

(53a)

(53b)

在时刻t，除压比pr和prc是未知量外，其他参数均是已知量。

采用牛顿-雷伏生法(Newton-Raphson method)，式(53)非线性方程组可线性化，

a51Δpr+a52Δpcr=d5

(54a)

a61Δpr+a62Δpcr=d6

(54b)

其中：

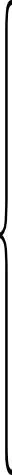
(54c)

式中δ>0为pr的微小增量，可取δ=10-7。

当由式(54)计算得到Δpr和Δpcr时，令

(55a)

pcr=pcr+Δpcr

(55b)

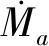
3.4 特例

特例1：初始工况压力罐存在气体。在此情况下，空气阀补气式压力罐的水力瞬变将从阶段4开始，然后在阶段2—4之间变化。

特例2：不考虑空气阀-检修阀-连接管高度的影响，即取高程Zat=Zct。在此情况下，水力瞬变过程只存在阶段2—4，且阶段4的水力瞬变可采用阶段3的计算模型，这时压力罐水位Hs=Hc>Zct、Ma=Mac0为常数(空气阀处于关闭状态)。

特例3：空气阀为真空破坏阀且压力罐高程Zmt=Zct，即图2(a)中的空气阀补气式压力罐转化为图2(b)真空破坏阀补气式压力罐。在此情况下，水力瞬变过程只存在阶段1和3。

特例4：图2(a)真空破坏阀被空气阀代替，即空气阀调压室，容许进气和排气。在此情况下，水力瞬变过程也可采用阶段1和3程序计算。

4 工程算例

下面以文献[12]泵站加压输水工程为例，计算比较分别设置空气阀、空气阀调压室及真空破坏阀补气式压力罐时的水击防护效果。需要说明的是，空气阀调压室就是在输水管上安装一垂直竖管，然后在其封闭顶盖上设置复合式空气阀的水力控制装置。

计算条件：空气阀进排气孔径为0.1 m，真空破坏阀进气孔径0.1 m，空气阀位置列于表1。初始条件：6台泵运行，额定转速，蝶阀全开。液控蝶阀两段关闭规律：0～2 s，y=1.0～0.1；2～20 s，y=0.1～0.0。

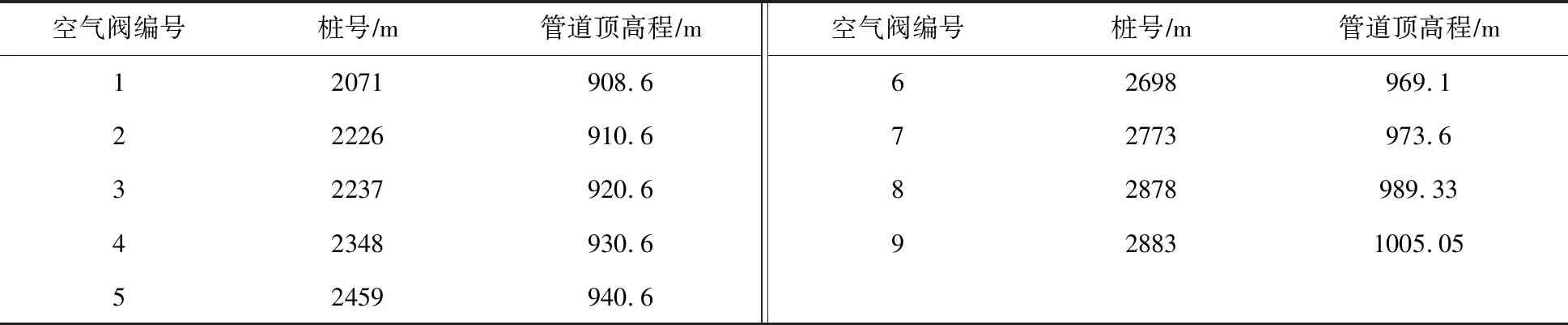
表1 空气阀布置位置及对应高程

表2列出了6台泵同时事故断电、液控蝶阀两段线性关闭条件下水力瞬变计算的特征参数，其中：h、Ds、dw分别为空气阀-检修阀-连接管、空气阀调压室、真空破坏阀补气式压力罐的高度、内径、阻抗孔直径；nmax为机组反向最大转速相对值，负号“-”表示反转；Hmax为输水管最大水压；Hmin为输水管最小水压，负号“-”表示负压；序号1和2是只设空气阀的结果；序号3、4是将空气阀更换为空气阀调压室的计算结果；序号5是将空气阀更换为真空破坏阀补气式压力罐的计算结果。

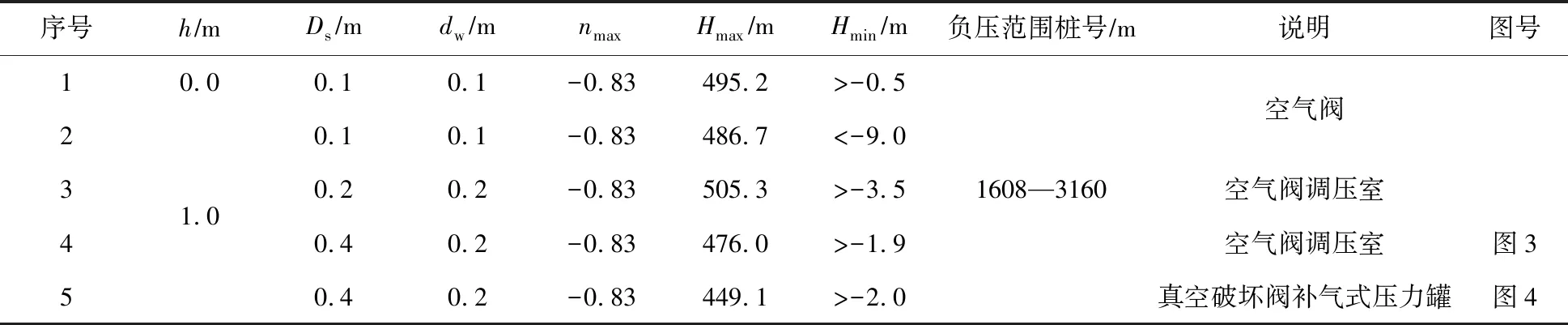
表2 水力过渡过程特征参数一览表

需要说明的是，在计算空气阀调压室和真空破坏阀补气式压力罐水力瞬变的过程中，没有考虑对应空气阀-检修阀-连接管高度的影响，表2中h和Ds分别为调压室或压力罐的高度和直径。

根据表2，可得下述结论：

(1)当出水管只设空气阀时，则空气阀-检修阀-连接管高度h=1.0 m时计算的Hmin比h=0.0 m时的小得多，在一些位置Hmin达到水体汽化压力(-9.0 m)，这意味着减小连接管高度有利于降低液体汽化的风险；

(2)当用空气阀调压室更换出水管空气阀时，随着调压室直径Ds和阻抗孔孔径dw增加到一定程度，不仅Hmax减小，而且Hmin也增加，例如，当使Ds和dw分别从0.1 m增加到0.4 m和0.2 m时，则Hmax从486.7 m减小到476.0 m，而Hmin从-9.0 m增加到-3.5 m；

(3)当把空气阀调压室更换为真空破坏阀补气式压力罐时，在调压室与压力罐高度、直径、阻抗孔孔径相同的条件下，真空破坏阀补气式压力罐比空气阀调压室的最大水压显著减小，相差达27 m；而两者最小水压相差微小，约为0.1 m；

(4)空气阀、空气阀调压室、真空破坏阀补气式压力罐对机组反向最大转速的影响微小。

压力罐大小及阻抗孔直径对水锤防护效果有很大影响，可通过水力过渡过程计算确定，以确保压力罐体内气体不流入输水管。

图3和图4示出了水泵出水管分别设置空气阀调压室和真空破坏阀补气式压力罐典型工况的水力瞬变曲线，包括调压室和压力罐的水位随时间的瞬变曲线。当Ds=0.4 m、dw=0.2 m时，桩号2071 m处空气阀调压室和压力罐水位Hs与空气阀顶部高程差(Hs-Zat)min>-0.8 m，表示调压室最低水位Hsmin在输水管顶高程以上，气体不会进入输水管，这对于输水安全性是非常有利的，因为在这种情况下，机组可以重新启动，无需经历排气过程。

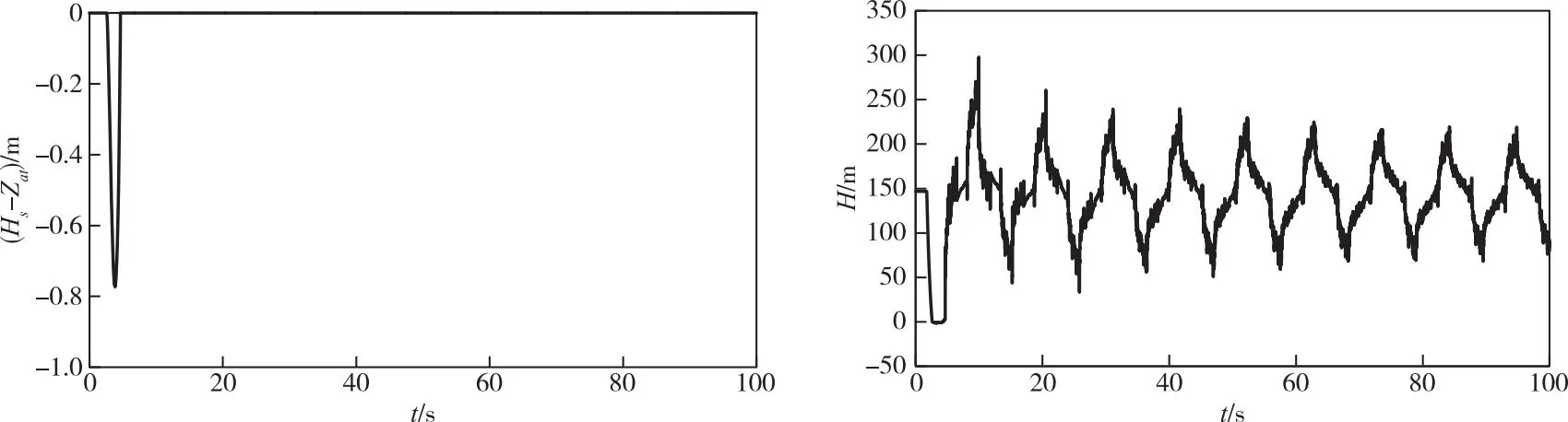
图3 空气阀调压室水位Hs与底部水压H随时间t的变化(桩号2071 m处)

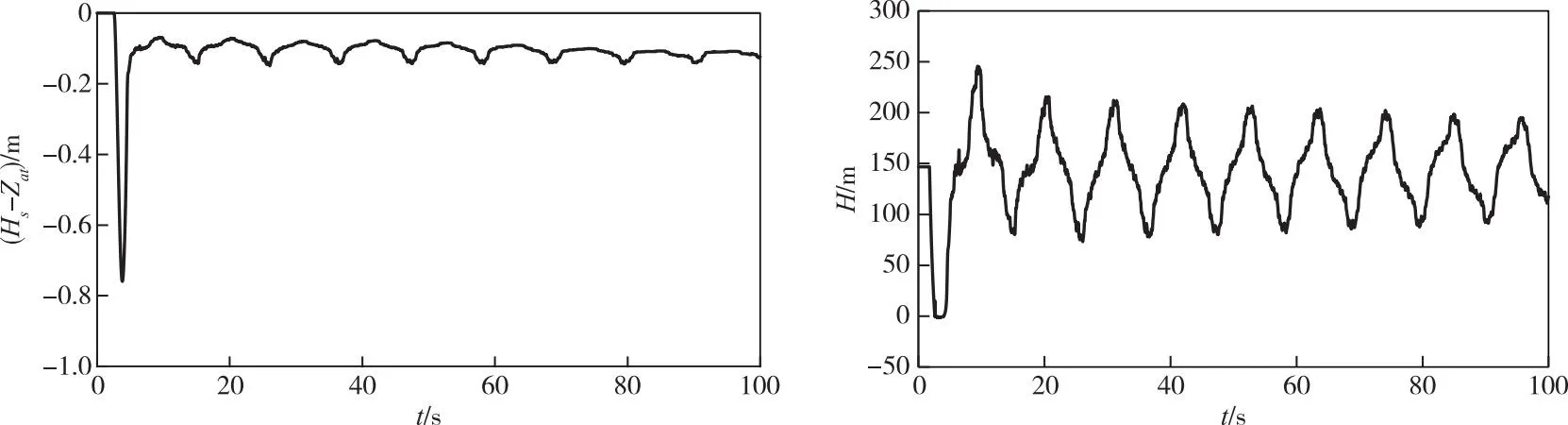
图4 真空破坏阀补气式压力罐水位Hs与底部水压H随时间t的变化(桩号2071 m处)

5 结论

本文提出了水击补气式压力罐装置的设计方法及水力瞬变数值仿真数学模型，并以一个实际泵站加压输水工程为例，计算比较了分别设置空气阀、空气阀调压室及真空破坏阀补气式压力罐时的水击防护效果，结果表明：(1)减小空气阀连接管高度有利于降低液体汽化的风险；(2)当用空气阀调压室更换空气阀时，不仅可以使最大水压减小，而且使最小水压增加；(3)当把空气阀调压室更换为真空破坏阀补气式压力罐时，在空气阀和真空破坏阀孔径、流量系数相同及调压室和压力罐结构参数也相同条件下，真空破坏阀补气式压力罐具有更好的水击防护作用；(4)合理地选择水击补气式压力罐的直径和高度，可以防止气体进入输水管，这对于输水安全性是非常有利的。

需要说明的是，水击补气式压力罐装置的研究处于初级阶段，其设置位置、数量、体型参数与工程的负压防护标准之间的关系需要进一步研究，特别是压力罐内气体的溶解规律。