基于SARIMA模型的近岸海表温度短期预报研究

赵强，王擎宇，舒志光

（自然资源部宁波海洋中心，浙江宁波 315012）

0 引言

近岸海表温度（Sea Surface Temperature,SST，简称海温）与渔业养殖、滨海旅游等人类生产生活息息相关，是海洋预报的主要工作内容之一。目前常用的海温预报方法主要有三类[1]：经验预报、数值预报和统计预报。经验预报是根据海温变化的周期性和持续性、结合天气系统特征进行预报，预报质量多取决于预报员的工作经验，预报产品通常为日平均海温或日最高、最低海温，难以满足日益增长的精细化海洋预报需求。数值预报则基于海洋动力学方程组，以气温、短波辐射、感热、风、潮等气象和海洋预报要素为强迫场驱动海温初始场，获得高时空分辨率的海温预报结果。但由于受到地形分辨率、观测数据、初始场和强迫场质量、模型参数取值不确定等因素限制，海温数值预报结果的准确度在近岸往往会下降，需要结合各类释用技术提高预报结果的可靠性[2-3]。统计预报则利用回归分析、聚类分析、主成分分析、相似分析等时间序列分析方法[4]，通过海温数据自身特征或海温与气温、气压等不同数据间的关系和规律探究数据的变化趋势。它是一种客观统计方法，计算效率相对较高，特别适合在具备观测基础的单点开展。

自回归积分滑动平均（Autoregressive Integrated Moving Average，ARIMA）是一种经典的时间序列分析和预测方法[5]，它综合了自回归（Autoregressive，AR）和滑动平均（Moving Average，MA）的特点，通过引入差分计算，满足了AR 和MA 对时间序列平稳性的要求，被广泛应用于社会和自然科学的各个领域。周期性自回归积分滑动平均（Seasonal Autoregressive Integrated Moving Average，SARIMA）是在ARIMA的基础上引入与数据周期性相关的参数，更适用于具有显著周期特征数据的预测分析[6]。

在海洋领域，ARIMA 及相关方法已被应用于赤潮和海温的季节和年际趋势预测研究[7-10]以及潮位和浪高的单步短时临近预测[11-12]，而其在短期预报特别是近岸海温短期预报方面的准确度尚不明确。目前，国内各海洋预报机构面向公众提供的近岸海温预报多为基于人工经验或数值预报得到的单点预报，预报时效多为24 h，预报产品为日平均海表温度或日最高、最低海表温度。本文利用石浦海洋站实测海表温度，采用SARIMA 方法构建了一个预报时效为72 h 的逐时海表温度预报模型，计算了模型预报结果误差，探讨了输入数据的时间分辨率和时长对预报误差的影响。研究结果对近岸海温的短期预报工作具有参考作用。

1 数据来源

本文所使用的数据为石浦海洋站2020 年1 月1日—2021 年12 月31 日的逐时海表温度（见图1）。石浦海洋站位于浙江省宁波市象山县石浦镇东门岛，为国家标准海洋站。海温测量采用YZY4 型温度传感器，测量范围为-5～50 ℃，测量精度为0.1 ℃。

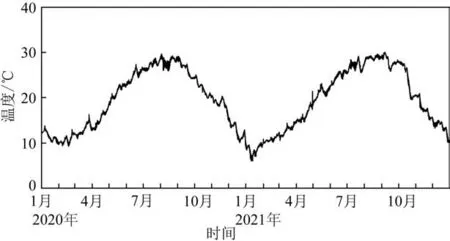
图1 石浦海洋站2020年1月1日—2021年12月31日逐时海表温度Fig.1 Hourly SST at Shipu Station from Jan 1,2020 to Dec 31,2021

2 SARIMA模型构建

2.1 SARIMA模型

SARIMA 模型通常写作SARIMA(p,d,q) (P,D,Q)s，其中p、d、q分别表示自回归、差分和滑动平均的阶数，而P、D、Q则表示周期为s的周期性自回归、差分和滑动平均的阶数。模型的数学表达式为[13]：

式中：yt为t时刻的时间序列值；εt为t时刻的白噪声序列值；c为常数项；B为延迟算子；Bs表示将yt在时间上向后移s次，即Bsyt=yt-s；ϕp(B)和θq(B)分别表示p阶自回归多项式和q阶滑动平均多项式；ΦP(Bs)和ΘQ(Bs)分别表示周期为s的P阶周期性自回归多项式和Q阶周期性滑动平均多项式。

由此可见，一个SARIMA 模型包含p、d、q、s、P、D、Q共7 个参数，这些参数的确定过程称为模型定阶。

2.2 观测数据前处理

2.2.1 平稳性检验

平稳性是指时间序列在未来的一段时期内能沿着现有的形态持续下去、不存在随时间变化的趋势性或者周期性，即序列的均值和方差不随时间发生明显变化[14]。若时间序列为非平稳，需要通过差分将其转化为平稳时间序列，以满足自回归和滑动平均模型的计算要求。

时间序列的平稳性检验可以通过数据曲线直观判断，也可以通过ADF 检验（Augmented Dickey-Fuller Test）[15]等单位根检验方法进行判断。若存在单位根，则说明时间序列存在趋势性或周期性，是非平稳的。近岸海温在长周期上受季节变化的影响，在短周期上受气温日变化和潮汐等周期性因素的影响，显然是非平稳的。ADF 检验的结果也显示其存在单位根，因此需要进行差分运算以消除其周期性。

2.2.2 非白噪声检验

非白噪声检验是对时间序列的自相关性进行检验，通常采用Ljung-Box Q 检验方法[5]。若通过检测，则时间序列为非白噪声，即一个时刻的观测值会对某时刻之后的观测值产生影响，意味着该时间序列是可预测的；否则，该时间序列为白噪声，不可预测。对石浦站逐时海表温度数据的一阶差分进行非白噪声检验，结果显示其为非白噪声，即可通过数据的自身特征进行预测。

2.3 模型定阶

SARIMA(p,d,q)(P,D,Q)s模型有7个参数需要确定。周期参数s可以通过分析时间序列的特征来确定。对逐时海表温度数据做调和分析，前10位成分的周期见表1，其中包括1 个年周期SA，1 个半年周期SSA，2 个月周期MSM、MM，2 个半月周期MSF、MF，1 个日周期S1，3 个半日周期M2、H2、S2。短期逐时预报不考虑长周期，因此s取12。近岸逐时海温为非平稳时间序列，通过1 阶差分或1 阶周期性差分都可将其转变为平稳时间序列，因此差分参数d和D可以取0 或1。自回归参数p和P、滑动平均参数q和Q的取值可先根据时间序列的自相关系数（Auto-Correlation Function，ACF）拖尾和偏自相关系数（Partial Auto-Correlation Coefficient，PACF）截尾的性质进行初步判断，之后利用贝叶斯信息准则（Bayesian Information Criterion，BIC）、热力图、误差评估等方法结合网格搜索进行确定。

表1 石浦海洋站2 a逐时海表水温调和分析结果Tab.1 Harmonic analysis result of the 2-year hourly SST at Shipu Station

由于本文的目的是构建一个短期预报模型，因此对SARIMA 模型赋以不同的参数值，并比较各组参数值下的模型预报结果误差，最终选择其中预报误差最小的一组参数作为最终参数。模型的输入数据为366 d 的逐时海温，输出数据为之后0～72 h的逐时海温预报结果，通过计算模型预报误差进行比较评估。为减少评估结果的偶然性和季节性并充分利用2 a的海温实测数据，本文开展了360组预报模型计算，每组输入数据的开始时间皆以1 d 为间隔后延，即第1 组的输入数据为2020 年1 月1 日00时（北京时，下同）—12月31日24时的逐时海温，计算2021 年1 月1 日00 时—1 月3 日24 时的预报误差，第2 组的输入数据为2020 年1 月2 日00 时—2021 年1 月1 日24 时的逐时海温，计算2021 年1 月2 日00 时—1 月4 日24 时的预报误差，以此类推。每组都重新计算模型中的自回归系数和滑动平均系数，共得到360 组预报误差。每组误差包括平均绝对误差（Mean Absolute Error,MAE）、平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）和均方根误差（Root Mean Square Error，RMSE），并按照0～24 h、24～48 h、48～72 h 的预报时效进行划分。比较不同参数取值下模型预报误差的平均值，结果见表2，受篇幅限制，仅列出部分误差较小的模型参数。

表2 不同参数下SARIMA模型的预报误差Tab.2 Forecasting errors of SARIMA model under different parameters

从结果来看，模型预报误差随预报时效的增加而明显增大，但同一预报时效、不同参数的模型预报误差较为接近，这与近岸海温受潮位影响较强且变化相对缓慢有关。综合来看，SARIMA(1,0,1)(1,1,0)12模型的预报误差最小。

3 结果和讨论

3.1 输入数据时间分辨率对预报结果的影响

SARIMA(1,0,1)(1,1,0)12模型中的周期参数值12与该海域占主导地位的M2 半日分潮的潮周期12.42 h 存在差异，这导致了预报海温与实测海温之间的相位差。以2021 年1 月10 日00 时起SARIMA(1,0,1)(1,1,0)12模型0～72 h 的预报结果为例（见图2），与实测海温相比，预报海温的相位随着预报时效的增加不断向前偏移。由于SARIMA 模型的参数只能取整数，如果周期参数值取13，预报结果的相位则会随着预报时效的增加不断向后偏移。

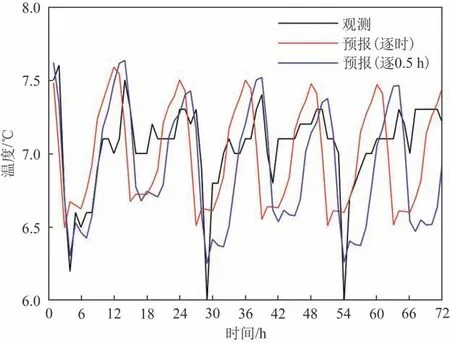
图2 2021年1月10日起0～72 h海温预报结果与观测的对比Fig.2 The 0～72 h hourly SST observations and forecasts starting from Jan 10,2021

调整输入数据的时间分辨率可以减小预报结果的相位偏移。利用线性插值将原始的逐时海温观测数据内插为逐0.5 h 并作为SARIMA 模型的输入数值，周期参数s设为25，构建SARIMA(2,0,2)(2,1,0)25模型并计算整点预报误差。相较于采用逐时输入数据的SARIMA(1,0,1)(1,1,0)12模型，SARIMA(2,0,2)(2,1,0)25模型预报结果的相位与观测更为一致（见图2），预报误差也相应减小（见表3），0～24 h、24～48 h、48～72 h 的MAE 平均值分别较SARIMA(1,0,1)(1,1,0)12模型下降了12.87%、8.62%、5.63%，RMSE平均值下降了12.50%、8.76%、5.81%。

表3 不同输入数据时间分辨率下SARIMA模型的预报误差Tab.3 Forecasting errors of SARIMA model with different time resolution of inputs

将输入数据的时间分辨率进一步提高到逐6 min 并构建SARIMA(10,0,10)(2,1,0)124模型，相较于SARIMA(2,0,2)(2,1,0)25模型，预报MAE平均值仅下降了0.001～0.002 ℃。究其原因，当采用逐时输入数据时，周期参数为12，对应预报结果的周期为12 h，与M2 分潮的潮周期相比，每个周期的相位差为0.42 h，对应24 h和72 h的相位差分别为0.84 h和2.52 h；当采用逐0.5 h 输入数据时，周期参数为25，对应预报结果的周期为12.5 h，每个周期的相位差为0.08 h，对应24 h和72 h的相位差分别为0.16 h和0.48 h，受逐时预报结果时间分辨率的限制，低于0.5 h 的相位差不会体现在预报结果和观测值的对比曲线上。同理，进一步提高输入数据的时间分辨率对于72 h 逐时预报结果的改进不明显，而且随着输入数据时间分辨率的提高，计算数据量也会提高，计算效率相应下降。由此可见，以逐0.5 h 数据作为模型输入已经可以满足72 h 逐时海温预报的要求。

3.2 输入数据时长对预报结果的影响

基于SARIMA(2,0,2)(2,1,0)25模型测试不同输入数据时长（366 d、183 d、90 d、30 d、10 d、5 d）对预报误差的影响，结果见表4。预报误差总体上是随输入数据时长的减少而增大的，且预报时效越长，误差增幅也越大。当输入数据时长为5 d 时，0～24 h、24～48 h、48～72 h 的预报MAE 平均值分别为0.206 ℃、0.453 ℃、0.755 ℃。利用近岸海表温度变化存在周期性且相对缓慢的特点，采用一种极简的、低技巧的预报方式，即直接复制当前24 h 的实测数据作为未来0～24 h、24～48 h、48～72 h 的预报结果，其对应的MAE 平均值分别为0.275 ℃、0.471 ℃、0.628 ℃。由此可见，当输入数据时长为5 d 时，对于当前的预报点，SARIMA(2,0,2)(2,1,0)25模型48～72 h 的预报精度已经接近或低于上述低技巧的预报方式，不具备实际应用价值。

表4 不同输入数据时长下SARIMA（2，0，2）（2，1，0）25模型的预报误差Tab.4 Forecasting errors of SARIMA（2，0，2）（2，1，0）25 model at different input data lengths

比较183 d 和90 d 输入数据时长的模型预报误差随时间的分布，并未发现183 d 预报误差较高的原因，其是否为普遍规律还有待引入更多站点、更长时间序列的数据加以研究。

3.3 预报误差和预报结果评分

图3 为采用SARIMA(2,0,2)(2,1,0)25模型计算得到的石浦海洋站2021 年1 月1 日—12 月26 日0～24 h表层海温逐时预报结果和误差。从图中可以看出，0～24 h 逐时预报误差多在±0.5℃以下，其占比为93.84%，误差分布没有呈现显著的周期特征。较大的误差多出现在海温急剧变化的时段，如2021年11 月8 日，受强冷空气影响，实测海温在4 h 内从20.4 ℃下降到17.8 ℃，降幅为2.6 ℃，而对应时段最大预报误差达到-3.3 ℃。由于没有考虑气象要素，SARIMA 模型在气象条件发生短期剧烈变化或发展趋势发生反转时的预报精度相对较低，引入气象预报数据可能会改善这些时段的海温预报精度，但由于气象变化对近岸海温的影响具有复杂性[16]，也必然会引入新的误差，其预报效果还有待进一步研究。

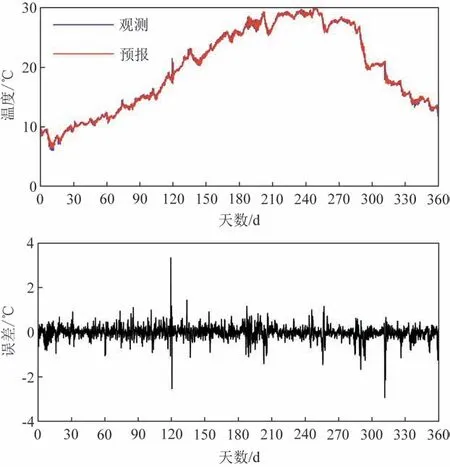
图3 SARIMA(2,0,2)(2,1,0)25模型计算得到的石浦海洋站0～24 h表层海温逐时预报结果和误差Fig.3 The 0～24 h hourly SST forecasts and the errors at Shipu Station from the SARIMA(2,0,2)(2,1,0)25 model

图4 为采用SARIMA(2,0,2)(2,1,0)25模型计算得到的石浦海洋站2021 年1 月1 日—12 月26 日日平均、日最高、日最低海温的预报误差图。日平均海温预报误差为-1.26～0.63 ℃，MAE 为0.13 ℃；日最高海温预报误差为-1.73～2.45 ℃，MAE 为0.22 ℃；日最低海温预报误差为-2.82～1.19 ℃，MAE 为0.18 ℃。

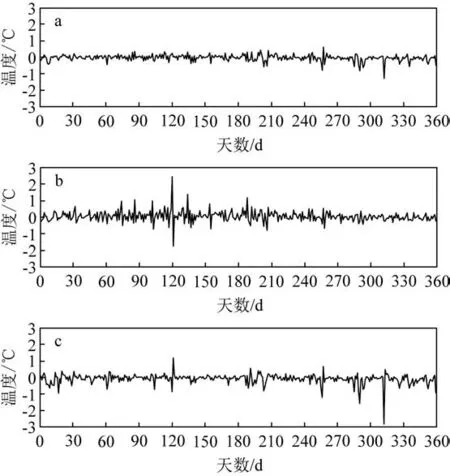
图4 SARIMA(2,0,2)(2,1,0)25模型计算得到的石浦海洋站日平均（a）、日最高（b）、日最低（c）海温预报误差Fig.4 The forecasting errors of daily average SST,daily maximum SST and daily minimum SST at Shipu Station from the SARIMA(2,0,2)(2,1,0)25 model

按照《海洋预报结果准确性检验评估方法（GB/T 41165—2021）》[17]的要求对日平均海温预报结果的绝对误差进行评估，按照“表层海水温度绝对误差不大于2 ℃时为满分100 分；……每相差0.1 ℃扣5分”的标准，SARIMA(2,0,2)(2,1,0)25模型0～24 h 日平均温度的预报质量得分在360 d 内皆为100 分，24～48 h 和48～72 h 预报质量的平均得分分别为99.94分和99.49分。鉴于现阶段近岸海温预报产品多为日最高、最低海温，本文也根据《海水浴场海洋环境预报技术导则》中的海温预报质量评分标准，对日最高、最低海温的预报质量进行综合评分。公式如下：

式中：A和B分别表示预报的最低和最高海温；C表示实测的日平均海温；R表示海表水温预报绝对误差。质量评分根据R值所在区间确定。经计算，SARIMA(2,0,2)(2,1,0)25模型0～24 h 海温预报质量得分为100 分、95 分、90 分及90 分以下的天数占比分别为75.28%、18.61%、4.44%和1.67%，最低得分为60 分，平均得分为98.28 分；24～48 h 和48～72 h的预报平均得分为93.69分和88.22分。

3.4 与其它方法预报误差的比较

将2021 年石浦站SARIMA(2,0,2)(2,1,0)25模型0～24 h 海温预报结果的日平均值与同期人工预报结果进行比较。SARIMA 模型预报的MAE 为0.131 ℃，最大绝对误差为1.262 ℃；人工预报的MAE 为0.401 ℃，最大绝对误差为2.633 ℃。SARIMA 模型预报结果优于人工预报结果的天数占比为82.22%。

李燕等[18]基于逐步回归法，采用海温、气温、降水、风速等数据在沿海多个站点建立了单站日均海温短期预报模型，1 d 预报的MAE 为0.177～0.544 ℃；匡晓迪等[2]基于BP（Back Propagation）神经网络方法，采用气象数值预报结果、舟山站海温经验预报和海温观测数据对近岸海温数值预报结果进行释用，1 d预报的MAE为0.88 ℃；林小刚等[19]基于长短期记忆网络方法（Long Short-Term Memory Networks,LSTM），采用气象数值预报结果和日均海温观测数据建立了粤东7个站点的近岸海温预报模型，1 d 预报的MAE 为0.24～0.40 ℃；王兆毅等[20]基于偏差订正方法，采用海洋站和浮标的逐时海温数据对中国沿海213个基础预报单元的海温数值预报结果进行订正，0～24 h、24～48 h、48～72 h预报的MAE 平均值分别为0.17 ℃、0.30 ℃和0.38 ℃。忽略预报区域和预报时段的差异，SARIMA 模型在日均海温和逐时海温预报方面都可以获得较优的预报结果。

4 结论

周期性自回归积分滑动平均（SARIMA）是一种适用于具有显著周期特征的数据序列的客观统计分析方法。本文基于石浦海洋站2020年1月1日—2021 年12 月31 日的逐时海表温度观测数据，采用SARIMA 方法构建了72 h 逐时海温预报模型，根据观测数据的周期特征和模型预报误差确定了模型参数。当采用逐时观测数据作为SARIMA 模型输入时，由于模型的周期参数只能取整数值，与在该海域占主导地位的M2分潮的潮周期12.42 h存在差异，导致预报结果与实测数据之间存在相位差，且相位差随着预报时效的增加而不断增大。将模型输入数据的时间分辨率提高到逐0.5 h，预报结果与观测数据的相位更为一致，预报误差更小。进一步提高输入数据的时间分辨率，对72 h 逐时预报结果准确度的提升作用不明显。模型输入数据时长会对预报误差产生影响，总体上看，预报误差会随输入数据时长的减小而增大，且误差增幅随预报时效的增加而增大。经比选，采用366 d 观测海温内插为逐0.5 h数据作为输入构建的SARIMA(2,0,2)(2,1,0)25模型的预报结果较优。2021 年1 月1 日—12月26 日石浦海洋站0～24 h、24～48 h、48～72 h预报时效的海温预报的MAE平均值分别为0.176 ℃、0.350 ℃、0.520 ℃，MAPE平均值为1.012%、2.005%、2.982%，RMSE 平均值为0.217 ℃、0.396 ℃、0.567 ℃，参照相关海温预报质量评分标准，对应时效日平均海温预报质量得分平均值为100 分、99.94分、99.49 分，日最高和最低海温预报质量综合得分平均值为98.28分、93.69分、88.22分。

总的来看，SARIMA 模型在日均海温和逐时海温预报方面都可以获得较优的预报结果。由于没有考虑气象要素，SARIMA 模型在气象条件发生短期剧烈变化或发展趋势发生反转时的预报精度相对较低，提高这些时段的预报精度是下一步的研究方向。