Wavewatch Ⅲ模拟和统计方法在最大波高预报方面的评测分析

王娟娟，侯放，吴淑萍，王久珂

（1.国家海洋环境预报中心，北京 100081；2.河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098；3.国家海洋环境预报中心自然资源部海洋灾害预报技术重点实验室，北京 100081）

0 引言

海浪是海洋上层最普遍的物理过程，对海洋工程、海洋军事和航行安全等都有非常重要的影响，尤其是海面瞬时出现的最大波高，可能对船舶和涉海作业造成巨大影响，甚至造成严重的人员伤亡和经济损失。因此，最大波高是表征海浪强度和危险程度的重要指标，可靠、稳定、长期的最大波高预报具有重要的实用价值。

早在1952 年，LONGUST-HIGGINS[1]就提出了基于瑞利分布的最大波高理论公式：

式中:Hmax为最大波高；N为统计时段内通过某个位置的波的数量；Hs为有效波高。FORRISTALL[2]基于墨西哥湾的海浪观测并结合LONGUSTHIGGINS 的理论公式分析，对波数N提出了一个校正系数。而FENG 等[3]在FORRISTALL 公式的基础上又引入了有效波高的因子。文铖等[4-5]基于挪威北海10年的船测波面资料，分析波陡和谱宽度对最大波高的影响，结果发现随着波陡和谱宽度的增加，Hmax和Hs的比值逐渐减小，研究也拟合出基于谱宽度参数的最大波高公式。曹广随等[6]探讨了海浪谱对最大波高的影响特性，并给出了考虑谱型因子的最大波高公式。以上最大波高计算公式都是基于瑞利分布得到的半理论或经验公式，而瑞利分布本身是在波面线性和窄谱假定的前提下得到的，不能体现海浪的非线性效应[7]。

部分学者基于观测资料的统计回归分析，建立了某个关注海域的Hmax和Hs的线性关系用于计算Hmax。滕学春等[8]利用沿岸台站的短期海浪观测资料开展分析，针对海上累年的最大波高，提出了水文和气象两种计算方法。朱智慧等[9]对5 个浮标站逐时的观测资料进行回归分析，认为上海沿海的Hmax/Hs在1.45～1.47 之间。周媛媛等[10]也采用同样的回归分析方法，基于浮标观测海浪资料，得到渤海、黄海、东海的Hmax/Hs分别为1.36、1.40 和1.43。采用线性回归关系计算最大波高是最简单的方式，但是现场观测耗资昂贵，而且耗时较长，难以满足大范围海域的预报需要。

在我国国家级和省级海洋预报机构，一般采用有效波高乘以固定系数的方法来预报最大波高，固定系数的数值一般根据局部海域的观测资料统计获得。这种预报方式虽然简单，但是固定系数的选取严重依赖于观测，而且也没有考虑不同位置的空间差异性以及Hmax和Hs的非线性特征。

目前，以海浪谱模型为基础的数值模拟是海浪预报的主要手段，该方法具有预报精度高、预报时效长、运行稳健等多种优点。最常见的海浪谱模型为第三代波浪模型Wavewatch Ⅲ（WWⅢ）和海浪模式Simulating Waves Nearshore（SWAN），国家海洋环境预报中心目前业务化运行的海浪数值预报系统即采用WWⅢ模型构建。WWⅢ中已建立最大波高的算法，但其模拟精度如何以及与传统统计关系方法的差异怎样，目前都还未见有相关的研究结果，这正是本文拟解决的问题。

本文基于浮标观测、WWⅢ模拟和检验方法，开展了两次台风浪过程的后报模拟和6 个半月的预报，并分析了WWⅢ模拟与传统的统计关系方法的差异。

1 数据和方法

1.1 数据

为了满足海洋预报和海洋灾害预警的需要，自然资源部在中国近海布放了30 余个水文气象浮标，用于观测海洋气象和水文要素[11]。观测要素包括：风速、风向、气温、气压、相对湿度、水温、平均波高、平均波周期、有效波高、有效波周期、十分之一波高、十分之一波周期、最大波高、最大波周期等。数据精度分别为：有效波高0.1 m，风速0.1 m/s，有效波周期0.1 s，浮标位置0.01′。

本研究中采用该水文气象浮标的海浪观测结果，浮标位置参见文献[11-12]，中国的5个海区均有浮标布放。该数据在使用前经过了严格的质量控制，识别异常点的质控算法参考WANG 等[12]的方法，异常点包括：①观测值超出物理范围；②观测值连续超过6 h 不发生变化；③以一个月为滑动窗口，诊断与月均值或与后一时刻观测值的差超过5倍标准差的观测。对识别到的异常点进行剔除，只保留有效观测。观测时段为2019—2022年，数据间隔为1 h 或30 min，真实的海面高度采样窗口长度为1 024 s，对窗口内观测到的所有波进行统计计算，将得到的有效波高和最大波高等参数作为该整点或半点时刻的观测值。

1.2 数值模拟方法

采用国际主流的WWⅢ海浪模型（版本号为6.07），模拟海浪谱的频率范围设置为0.04～1.10 Hz，频率分割数为25，海浪方向分割数为36，计算网格的空间分辨率为0.1°，测试模拟区域为整个西北太平洋海域，即0°～45°N，95°～165°E。

为了在WWⅢ海浪模型中激活波峰和时空极值波高（即最大波高），需要在ww3_grid.inp 文件中指定MISC列表的STDX、STDY和STDT参数值，而不是默认的-1。STDX 和STDY 是计算极值的空间维度参数，模拟中采用一个网格的尺寸，本研究为10 km。STDT 是计算极值的时间长度统计参数。为了与浮标真实的海面水位采样窗口长度一致，时间统计参数STDT 统一设置为1 024 s，在业务化预报中采用1 h，与有效波高的输出间隔相匹配。

WWⅢ模型中时空极值最大波高的计算方法为对于给定的多维、统计上均匀和稳定的高斯随机波场，最大海面高程的超越概率通过欧拉示性数的平均值来近似获得[13]。WWⅢ中使用的时空极值模型是FEDELE[14]建立的时空极值高程模型，他还将其扩展到二阶非线性空间波场[15]，而BENETAZZO 等[16]将其推广到了时空场。BARBARIOL 等[17-18]通过数值模拟对这个时空极值线性模型进行了评估，FEDELE 等[15-16]同时使用立体成像验证了该模型对二阶非线性波的扩展。

根据这些模型，二阶非线性时空最大峰顶高度的超越概率近似为与表面高程的标准偏差σ、非线性阈值、时空统计区域内三维、二维和一维的波数量N3D、N2D和N1D等有关的函数。根据准确定性（Quasi-Determinism，QD）模型，对于具有线性极端波峰高度ηˉ1STm的波浪，其波峰—波谷的高度Hˉ1cm（最大波高，输出参数HCMAXE，单位为m）的预期值为:

式中：S(ω)为波频率谱。而是这种波谷的预期位移，即在预期线性极端波峰高度之前或之后的波谷。式（2）中的计算方法为：

式中：γ≈0.577 2 是欧拉常数；h1是最可能的无量纲极值（相对于标准偏差σ），为隐式方程（5）的最大解：

对于给定的线性波群，Hˉ1cm通常小于最大预期波高Hˉ1m（即最大波高，输出参数HMAXE，单位为m），计算方法为：

1.3 精度检验方法

选择6个误差参数，即平均偏差Eb、平均绝对误差Ea、均方根误差S、相对误差Er、分散指数Is、相关系数ρ，其中后三者是评估模拟精度的无量纲参数，只有通过显著性检验的相关系数才被采用，相关性假设检验p值小于0.05。将浮标观测认为是真值，利用二维网格数据的线性插值方法提取浮标位置的模拟值，将其与该时刻的浮标观测构成一组评估数据，计算6个参数。公式如下：

式中：F(i)和O(i)分别表示第i个数值预报值和浮标观测值；Fˉ和Oˉ分别表示数值预报值和浮标观测的平均值。相对误差只选取波高观测不低于1 m 的数据。

2 后报模拟

为了评估WWⅢ对最大波高的模拟能力，首先对两次典型的台风浪过程进行后报模拟。筛选2020 年第8 号台风“巴威”（强台风级）和第9 号台风“美莎克”（超强台风级）引起的重大海浪过程，最大波高的观测资料采用过程观测值较大的4 个浮标，即距离台风中心较近的4 个浮标MF06001、MF07001、MF05002、MF04001，它们与台风中心的距离为50～130 km，足以观测到台风造成的大浪。在两次台风浪过程中，MF06001 浮标观测的最大波高的过程极值为10 m，MF07001 为14 m，MF05002为7.9 m。

后报模拟采用了第五代大气再分析数据集（ERA-5）的海面再分析风场来驱动，该风场的空间分辨率为0.25°，时间分辨率为1 h。地形资料选择全球地形和水深数据ETOPO1。模拟计算时段为2020年7月15日—10月1日，WWⅢ冷启动，模拟输出时段为2020 年7 月25 日—10 月1 日的逐小时最大波高和有效波高，与浮标观测的最大波高对比见图1。

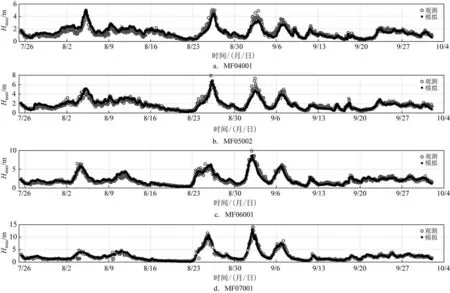
图1 浮标观测和数值模拟的最大波高对比Fig.1 Comparison of maximum wave height between buoy observation and numerical simulation

从图1 可以看出，数值模拟与浮标观测的吻合度非常高，采用检验方法计算4 个浮标的最大波高模拟误差，结果见表1。从表中可以看出，模拟值普遍存在一定的正偏差，Eb幅度在0.1 m 以内。Ea和S为0.26～0.64 m，由于海浪强度较大，因此绝对误差和均方根误差本身就会比平均误差偏大。而Er、Is和ρ属于无量纲的精度检验参数，更能普适地反映精度特征，4个浮标的Er均低于20%，Is均低于26%，ρ普遍高于0.90。

表1 模拟最大波高的精度评估参数Tab.1 Parameters for evaluating accuracy of maximum wave height simulation

对同时段的有效波高模拟值也进行了检验，误差参数见表2。结合有效波高和最大波高的精度对比结果（见图2）可以发现，最大波高的模拟精度整体略低于有效波高，其中两者高模拟的Is和ρ结果相当，而对于其余4个误差参数，最大波高的表现均差于有效波高。但是，这种模拟精度可以接受，最大波高大约是有效波高的1.4～1.5 倍，Eb、Ea和S本身也应该比有效波高大。而Er低于20%、ρ高于0.90 的精度水平已经足够可靠，可以应用于业务化预报。

表2 数值模拟有效波高的精度评估参数Tab.2 Parameters for evaluating accuracy of significant wave height simulation

图2 有效波高和最大波高的模拟误差对比Fig.2 Comparison of simulation error between significant wave height and maximum wave height

3 预报模拟

基于上述分析，我们开展了6 个半月的预报试验并评估了预报精度。风场采用中国气象局全球集合预报系统GRAPES 的预报海面风场，时段为2021年6月15日—12月31日，预报时效为120 h，输出每个0.1°网格点上的最大波高和有效波高，并评估了未来24 h 预报的最大波高模拟精度，结果见图3。最大波高的数值预报误差以及同时段的有效波高预报误差结果见表3。

表3 最大波高和有效波高的预报误差Tab.3 Forecast error of maximum wave height and significant wave height

图3 数值预报与观测的最大波高在不同海区的比较Fig.3 Comparison of the maximum wave height in different sea areas between numerical forecasts and observations

从结果可以看出，最大波高的模拟与观测吻合度较高，24 h 预报的Er低于18%，Is低于26%，ρ大于0.94。对于有量纲参数的Eb、Ea和S，最大波高都大于有效波高，但这与最大波高本身就比有效波高大有关；而对于无量纲的Er、Is和ρ，最大波高与有效波高的统计值非常接近，证明最大波高的模拟精度接近有效波高。与有效波高结果类似，在3 个海区的预报表现上，渤黄海的精度较差，东海和南海的精度更高。6 月15 日—12 月31 日这6 个半月的预报涵盖了台风浪和冷空气浪这两种典型的强海浪过程，预报精度具有良好的代表性，反映出WWⅢ模型对最大波高的数值模拟能力已经足以应用于业务化预报。

4 与统计关系的比较分析

为了研究WWⅢ数值模拟与统计关系方法在计算最大波高方面的差异，我们将对比分析两者的误差参数。已有研究中建立的Hmax和Hs之间的统计关系式均为一元一次线性方程，朱智慧等[9]认为上海沿海Hmax和Hs比值为1.45～1.47，周媛媛等[10]认为渤海、黄海、东海的Hmax和Hs比值分别为1.36、1.40和1.43。多数研究得到的Hmax和Hs的比值范围为1.36～1.47，因此取其均值1.42 作为一种统计关系（简称比值1.42 方法）；同时，根据本研究中所有浮标观测的Hmax和Hs比值，取其平均值1.52 作为另一种统计关系（简称比值1.52 方法），共同与数值模拟进行对比分析。

利用比值1.42 方法、比值1.52 方法和数值模拟可以获得最大波高与观测之间的误差参数（见图4和表4）。从中可以看出，3 种方法的Eb差异较大，比值1.42 方法存在-0.028 m 的负偏差，比值1.52 方法和数值模拟存在不超过0.1 m 的正偏差；3 种方法其余5 个误差参数的差异很小。总体来说，两种统计关系和数值模拟的精度相当，比值1.42 方法的精度略高。

表4 两种统计关系与数值模拟在计算最大波高方面的误差对比Tab.4 Error comparison of maximum wave height methods between two statistical relations and numerical simulation

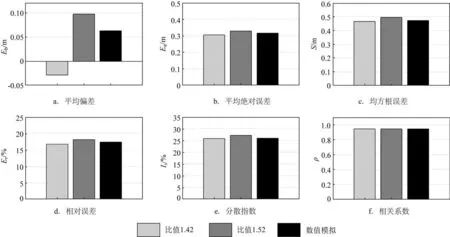
图4 两种统计关系方法与数值模拟方法计算的最大波高误差对比柱状图Fig.4 Histogram of maximum wave height error calculated by two statistical relationship methods and numerical simulation

数值模拟和观测的Hmax和Hs比值是变化的，而统计关系的比值是固定的，那么在不同的观测比值下，数值模拟和统计关系的精度是否有差异呢？为此，我们分析了在不同观测比值下3种方法的误差，观测比值的分析范围设置为1.1～2.0，划分间隔为0.05，分别计算每个区间范围内的6 个误差参数，对比结果见图5。

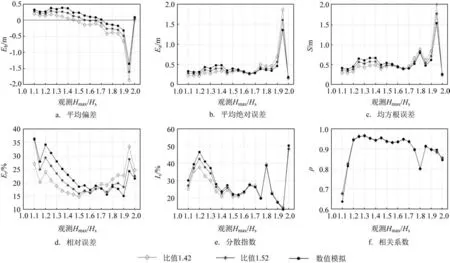
图5 两种统计关系与数值模拟的误差随观测的Hmax和Hs比值的变化Fig.5 Evolution of ratio of the observed Hmax and Hs,and the error between two statistical relationship methods and numerical simulation

从图中可以发现，3 种方法的偏差存在一致的特征，即随着比值的增大，Eb逐渐从正值降为负值，即计算的最大波高从偏大逐渐转为偏小，其中数值模拟的偏大程度最显著。当观测比值为1.95 时，3种方式的负偏差急剧增大，其中比值1.42 方法的负偏差达到了-1.87 m，数值模拟的负偏差最小，也达到-1.34 m。

对于误差参数Ea和S，当观测比值低于1.65 时，比值1.42 方法的精度较高；但是当观测比值大于1.65 时，数值模拟的精度最高，比值1.42 方法最差。Er也表现出与Ea和S相似的变化特征。当观测比值低于1.65 时，3 种方法Is的变化特征与上述类似，而当观测比值大于1.65 后，3 种方法的Is基本无差异。3种方法的ρ都基本一致。

概括来说，3种方式的精度特征为当观测Hmax和Hs比值低于1.65时，数值模拟的精度最差，比值1.42方法的精度最高，而当Hmax和Hs比值大于1.65 时，数值模拟的精度最高，比值1.42 方法最差。这个精度特征的原因可能与Hmax和Hs之间的非线性特征有关。KIM等[19]指出Hmax和Hs的线性回归关系在没有波破碎的情况下比较适用，而在有波破碎的条件下，两种波高的关系是高度非线性的。数值模拟中最大波高的计算方法是利用了考虑时空极值高程的模型[14]，并扩展到了二阶非线性时空波场[15-16]，因此其在非线性特征的表现上更好。当Hmax和Hs比值大于1.6甚至接近2时，代表出现了异常大的波甚至是畸形波或怪波，其危险性是非常大的，而统计关系使用了固定的比值系数，一般不超过1.5，这样是不可能计算出畸形波或怪波的。因此，在Hmax和Hs比值较高的情况下，数值模拟对最大波高的计算更具优势，更适合应用于海洋预警报服务和防灾减灾。

5 结论

基于WWⅢ模型和浮标观测，对两次台风浪过程的最大波高进行后报模拟，并开展了6 个半月的预报测试，据此评估了数值模拟的精度水平，并横向评价了其与统计关系方法的精度差异。主要结论如下：

①数值模拟得到的最大波高的精度略低于有效波高，但也达到了较高的精度水平，24 h预报的相对误差（最大波高不低于1 m）低于18%、相关系数高于0.94，即使是对于台风浪这种强过程的相对误差也低于20%、相关系数高于0.91。这表明数值模拟得出的最大波高精度可靠，可以用于业务化海浪预报。

②为了研究数值模拟与传统的统计关系方法在计算最大波高方面的差异，采用两种统计关系方法（Hmax和Hs比值为1.42和1.52）与WWⅢ结果进行对比分析，结果表明WWⅢ模拟的精度水平总体上与统计关系方法相当，但在Hmax和Hs比值大于1.65这种易出现危险的海况下，数值模拟具有更高的准确性，更适合应用于海浪预警报服务。