不完全信息Epsilon纳什均衡的航天器末端追逃博弈策略

汤 旭，叶 东，肖 岩，孙兆伟

（哈尔滨工业大学卫星技术研究所，哈尔滨 150001）

0 引言

随着太空技术的不断升级，空间航天器的功能日趋完备，越来越多的航天器具备了空间态势感知的能力［1-2］。当拦截航天器接近目标航天器时，目标方将采取机动策略加以躲避，这使得拦截航天器控制系统在应对新体系下迅速发展的空间攻防任务时面临着困境［3］。因此，在争夺战时空间信息优势的过程中，亟待发展新的轨道控制策略。

针对此类具有自主机动、自主决策能力的航天器拦截问题，需要对连续动态对抗的双边复杂态势进行研究，传统的单边优化拦截控制方法将不再适用［4］。此时，拦截器与目标存在利益冲突，构成博弈关系，空间拦截、交会对接问题也将发展成双方航天器间的追逃博弈问题［5］。此外，由于空间战场环境的限制、航天器固定指向以及传感器的约束，拦截器将不能完全获悉目标信息，导致拦截呈现不完全信息态势。因此，研究不完全信息下的航天器轨道追逃问题对于应对未来空间领域的新形势具有重要意义［6］。

针对目标具有机动能力的双边拦截博弈问题，应用最广泛的研究方法是微分对策理论，该理论已成熟应用于导弹拦截问题中。文献［7］基于简化的双积分系统导弹拦截模型，设计了导弹拦截矢量制导率，并分别给出了制导率在极坐标和球坐标下的分量表示，以便在不同坐标系下进行描述。文献［8］在拦截过程中考虑了存在角度测量有界噪声的情况，通过设计状态观测器实现对角度的估计并分别给出了不同噪声条件下脱靶量的估计值。文献［9］针对制导率包含拦截剩余时间且该时间难以确定的问题，建立了关于剩余时间的方程，并讨论了该方程的分叉现象，以求解最短拦截时间，从而实现快速拦截。尽管微分对策理论在导弹领域得到了广泛的应用，但在太空领域中仍有较大的提升空间。

与传统的空间交会拦截问题相比，航天器追逃博弈策略需要考虑博弈双方的控制策略。文献［10］将非线性拦截逃逸相对动力学简化为CW方程，根据拦截任务终止要求引入零控脱靶矢量将动力学方程降阶，采用拦截脱靶量和燃料消耗作为二次最优目标函数，推导了卫星轨道次优控制策略。文献［11］则以CW 方程为基础，推导了最优推力角博弈策略，并采用粒子群优化算法解决了协态变量初值难以确定的问题，得到了开环解。同时，通过预先生成一系列最优轨迹，并进行插值和外推，得到反馈控制策略的闭环解。文献［12］考虑了航天器追逃的双边博弈问题，提出了混合控制策略，以适配多任务的需求。通过博弈值函数与轨迹界栅判断是否需要执行策略切换，以实现追逃任务与自身任务的平衡。文献［13-14］对航天器远程拦截博弈问题进行了研究，针对协态变量初值难以确定的问题，通过遗传算法优化求解近似初值，然后将运动轨迹离散化，为各离散点配置状态，并使用非线性规划优化求解协态变量初值的精确值。文献［15］研究了航天器多段博弈拦截问题：在远程拦截段，基于微分对策理论分别给出了闭环鞍点解和开环鞍点解，两组解在形式上相同；在近程拦截段，考虑不同的指标函数，分别建立了不同的博弈策略。通过分析得出，实现拦截的充要条件是拦截器的推力幅值大于目标的推力幅值。文献［16］针对多航天器的末端拦截博弈问题，根据拦截空间是否具有防御器将博弈态势分为双星博弈和三星博弈，并提出了一种博弈切换策略，将三星博弈转化为分段的双星博弈，并将双边时间方程扩展到三星博弈中，使得拦截器能够在不被防御器反拦截的情况下快速拦截目标。

由于空间攻防时战场的不确定性、信息不对称等因素，航天器追逃任务中往往存在信息不完全的情况。因此，拦截航天器需要在有限时间内对目标航天器的不完全信息进行估计，以便实施有效的机动策略。在这种情况下，航天器追逃博弈理论可以为拦截任务提供有效的决策支持。针对不完全信息下的拦截问题，文献［17］研究了目标的逃逸防御问题，通过给定拦截器策略，考虑目标与防御器之间存在单向通讯或双向通讯的不同情况，建立了目标与防御器间的最优博弈策略。文献［18-19］中使用双积分系统作为动力学模型来探究目标信息不完全和动力学信息不完美的情况，将不完全信息和不完美信息视为扩展的状态变量，采用了增广原动力学的方法处理信息缺失问题。同时，设计了观测器对扩展状态进行有效估计。文献［20-21］中提出了一种基于状态观测的博弈值函数近似方法。该方法利用级数展开对博弈值函数进行近似，然后通过观测目标的状态信息对级数的各系数进行更新。该方法具有较高的计算效率和精度，已经在空间攻防任务中得到了广泛应用。文献［22-23］中考虑了模型不确定问题，首先预设了多种拦截弹可能采取的制导率，并设计了多个估计器并行计算不同情况下拦截弹的最优状态估计，并给出相应估计后验概率。然后，通过概率融合方法将不同估计器得到的最优状态估计和后验概率融合，得到更加准确的拦截弹制导率。最后，通过设计目标和防御器的协同制导率有效躲避了拦截。

虽然追逃博弈问题已经得到了广泛研究，但大多数研究都是以拦截器可以完全获得目标信息的假设为基础进行的，或者是基于简化的动力学模型研究不完全信息博弈，这与实际的航天器追逃博弈态势存在较大差异。因此，本文针对不完全信息下的航天器追逃博弈问题进行了研究，实现了在不完全信息下对目标的快速拦截。随着低轨目标拦截技术不断发展，任务能够快速准确地获得发射窗口［24］，该方法也将成为未来处理一类具备智能体特性的失控航天器的机动策略之一。通过快速接近不受地面指令控制的失控航天器，并将其引导到安全轨道，可以避免对其他航天器和空间设施造成威胁。

综合前文所述，本文针对不完全信息下航天器末端追逃博弈问题，首先建立了航天器末端拦截动力学模型，并给出了完全信息下的纳什均衡策略对。然后，考虑目标控制矩阵信息不完全的情况，设计了基于广义卡尔曼滤波的行为学习信息估计算法，并严格证明了所提出的不完全信息下微分博弈策略对满足Epsilon 纳什均衡。最后，通过仿真验证了算法的有效性和拦截的快速性。本策略不仅适用于航天器拦截任务，还可以作为星群中具备智能体特性的失控航天器的处理方法，具有实际应用价值。

1 航天器相对运动状态方程

在航天器末端拦截段，拦截航天器与目标航天器的相对距离远小于两星质心到地心的距离，因此在拦截卫星附近设置参考卫星O1，P为拦截航天器，如图1 所示。假设参考卫星运行在圆轨道，以参考卫星为原点，x轴沿着参考卫星地心矢径方向，z轴沿着轨道角动量方向，y轴满足右手定则，定义虚拟卫星轨道坐标系O1xyz［25］，在LVLH 坐标系下拦截器相对参考卫星的动力学方程可以简化为CW方程：

图1 拦截器与参考卫星Fig 1 Interceptor and reference satellite

式中：x，y，z为拦截器相对参考卫星的位置；ω为参考卫星的轨道角速度；ux，uy，uz分别为拦截器三轴方向上的控制输入。

由线性系统理论可得状态转移矩阵为：

式中的子矩阵［26］分别为：

式中：τ=t-t0，且满足(t，t0)=Φ(t，t0)A。

当τ=tf-t时，状态转移矩阵Φ满足(tf，t)=-Φ(tf，t)A。在该虚拟卫星轨道坐标系下，拦截器与目标动力学均满足CW方程，即：

式中：Ui(i=P，E)分别为拦截器P 以及目标E 的推力，且均满足幅值限制‖UP‖＜ρP，‖UE‖＜ρE。

定义拦截器与目标的相对状态为：

对其求导并将式（4）代入可得相对状态方程：

式中：CE=BP。

2 有限时间追逃博弈策略对

在末端博弈过程中，双方将围绕拦截结束时的距离展开争夺。拦截器尽可能以最小代价实现对目标的快速接近，而目标则尽可能以最小代价增大与拦截器之间的距离。因此，本文定义以下指标函数：

式中：S＞0为对称正定矩阵；Q≥0为对称半正定矩阵；RP＞0与RE＞0均为对称正定矩阵，且满足：

式中：I∈R3×3为单位阵。

定义如下哈密顿函数：

式中：λ为协态变量。

设协态变量与状态变量满足如下关系：

式中：P为对称正定阵，即P＞0，PT=P。

对式（12）求导，并将其与式（7）和式（11）代入式（13），可得黎卡提微分方程如式（14）所示。

因此，拦截器与目标的鞍点策略对为：

式中：P满足式（15），推力满足幅值限制‖UP‖≤ρP，‖UE‖≤ρE。

3 不完全信息下博弈策略设计

本节考虑拦截航天器无法获取目标航天器控制矩阵的不完全信息情况。在这种情况下，追逃博弈不再满足纳什均衡，因此本文采用Epsilon 纳什均衡（后文简写为ε-纳什均衡）［27］对其进行描述。此外，目标航天器实际采取式（16）中的博弈策略，掌握着博弈进程的完全信息，进而获得更好的逃逸性能。

假设1.在本节研究的情境下，拦截器在面对不完全信息时存在行为学习信息估计进程，而目标无法获取拦截器的实际机动策略。

注1.如果目标能够获取拦截器的实际策略，那么它将采取诱导策略来迷惑拦截器，而拦截器则会采取相应的对策来应对诱导策略。这种无限变化的过程可以被看作是一个无限维博弈，因为双方都在不断地改变自己的策略以适应对方的变化。为了避免这种情况，本文假设1 指出只有拦截器存在信息估计的策略，而目标不知道该过程和其实际机动策略。

定义扩展状态变量Y=[XPETrE]T，则扩展状态方程与量测方程为：

由于扩展状态方程的非线性，本文采用广义卡尔曼滤波（类EKF）对RE进行估计。定义标称状态为Yn，Zn，则在标称状态点对式（17）进行一阶泰勒展开可得：

式中：ΔY=Y-Yn，ΔZ=Z-Zn为状态偏差，Fn为雅克比矩阵，Hn为量测矩阵，具体形式如下：

式中：Φ(k，k-1)为状态转移矩阵，且Φ(k，k-1) ≈I+FnT，Wk-1为过程噪声，Vk为量测噪声，T为采样时间，且满足如下条件：

式中：Ψk为系统噪声序列的方差阵，为半正定阵；Rk为量测噪声序列的方差阵，为正定阵；δkj为Kronecker符号。

图2所示为不完全信息下的博弈控制策略流程，针对线性化的状态方程（21），采用卡尔曼滤波进行状态估计，此时的滤波方程为：

为了尽可能减小状态偏差，本文希望状态标称值尽可能接近于状态最优估计值。因此，可以将状态标称值设置为状态最优估计值，以减少估计误差。

式中：P*满足如下黎卡提方程：

且P*仍满足终端条件P*(tf)=S。

4 满足ε-纳什均衡的数学证明

在实际的空间攻防过程中，存在许多不确定性因素，例如战争迷雾、传感器约束、目标无规律机动等。这些因素导致了目标信息的不完全性，从而无法满足完全信息下的纳什均衡，因此完全信息策略不再适用。本节将严格证明所设计的微分博弈策略对满足ε-纳什均衡。这意味着，当策略对满足更加宽松的ε-纳什均衡时，可以确保拦截航天器处在不完全信息下的最劣情况时仍能获得近似最优解，并且目标航天器的机动策略不会对其收益带来较大影响。

定理1.设拦截航天器与目标航天器的动力学方程为式（7），指标函数采用式（8），拦截器实际采取的策略为式（25），记为，目标实际采取的策略为式（16），记为。此时博弈策略对形成ε-纳什均衡，即：

证.采取状态估计策略下，相应的航天器状态分别记为，协态变量记为λ*，此时的博弈策略对改写为：

将式（29）代入相对状态方程（7），并积分可得：

此时的指标函数为：

注2.当拦截器采取不同的机动策略时，会导致两者相对状态变量的不同，因此尽管目标都采取了最优策略，但是对应的控制输入却可能是不同的。综上所述，本文将这种情况下的目标策略记为。

此时的状态变量为：

此时的指标函数为：

同时，对式（13）进行积分，并结合横截条件可得：

式中：i为任意策略。

定义状态变量差为ΔX=X*-X+，协态变量差为Δλ=λ*-λ+，分别将式（30）、（33）和（35）代入得到：

对上式中的ΔXT(tf)SX+(tf)项进行积分变换，则有：

令τ1-t0=τ-tf，则有：

式中：λmax(·)表示矩阵的最大特征值，由函数积分有界性定理可知：

因此，不完全信息下的追逃博弈策略设计满足ε-纳什均衡。

5 仿真校验

为了验证所提出的行为学习信息估计追逃博弈策略在不完全信息条件下的有效性，本节进行了3 种不同情况的对比分析，包括完全信息、不完全信息和不完全信息条件下的信息估计博弈策略。

在完全信息条件下，假设双方都可以获取对方采取的纳什均衡策略和当前状态信息。而在不完全信息条件下，假设拦截器只获取到初始位置和对方可能采取的策略集合。在信息估计博弈条件下，本文考虑实际空间攻防中末端追逃场景，采用提出的不完全信息下ε-纳什均衡博弈策略追击目标。通过对比分析3 种不同条件下的末端追逃结果，本节评估了所提出的不完全信息ε-纳什均衡的航天器追逃博弈策略的有效性。

初始条件设定如下：假设拦截航天器与目标均运行在近地轨道附近，选取近地轨道上与其相近的卫星作为参考卫星，其轨道角速度ω=0.001 rad · s-1。拦截器与目标的初始位置分别为[1.5 0.5 0]Tkm，[0 0 0]Tkm，初始速度分别为[0 0 0]Tkm · s-1，[ -0.05 0 0.05]Tkm · s-1。

假设拦截器与目标的最大推力加速度均为10 m·s-2，广义Kalman 滤波中过程噪声方差阵为diag[10-610-610-60.25 × 10-60.25 × 10-60.25 × 10-61010]，量测噪声方差阵为diag[10-810-810-80.25 ×10-80.25 × 10-80.25 × 10-8]。

5.1 完全信息博弈

在这种情况下，拦截器可以精确获取到目标的控制矩阵RE。通过仿真，可以观察到图3和图4中展示的航天器三维运动轨迹和相对距离变化，在488 s时，拦截器成功地拦截了目标。此外，图5展示了完全信息博弈进程中拦截器的控制加速度变化情况。

图3 完全信息下航天器追逃轨迹Fig.3 Spacecraft pursuit-evasion trajectory under complete information

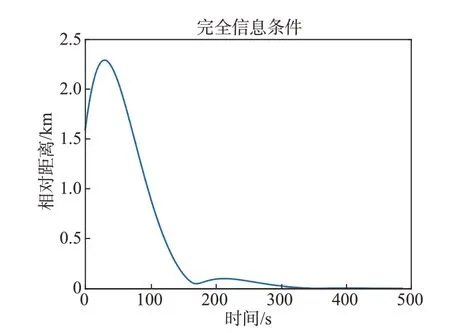
图4 完全信息下航天器相对距离Fig.4 Relative distance of spacecraft under complete information

图5 完全信息下拦截器控制加速度Fig.5 Control acceleration of the interceptor under complete information

5.2 不完全信息博弈

在这种情况下，拦截器无法准确获取到目标的控制矩阵，只能通过猜测该矩阵来设计拦截器策略，假设拦截器猜测的目标控制矩阵为=2 ×106I3。

通过仿真图6 可以看出航天器间追逃轨迹，且拦截器在1 979 s 时成功拦截了目标。然而，从图7中可以看出，拦截器与目标的相对距离变化很剧烈，经过多次震荡，拦截器才最终实现拦截。

图6 不完全信息下航天器追逃轨迹Fig.6 Spacecraft pursuit-evasion trajectory under incomplete information

图7 不完全信息下航天器相对距离Fig.7 Relative distance of spacecraft under incomplete information

通过比较图5 和图8 可以看出，由于拦截器是在猜测较大的值下决策的，该条件下的控制加速度表现出剧烈的振荡，拦截过程的控制性能显著下降。仿真结果表明，如果拦截器不能完全获得目标的信息，会导致拦截时间增加、拦截性能下降。因此，在航天器追逃控制中，对目标的不完全信息进行估计具有重要意义。

5.3 不完全信息下信息估计博弈策略

在这种情况下，拦截器采用信息估计的方法来适配目标的控制矩阵，从而建立不完全信息下的博弈策略。假设拦截器对目标控制矩阵的初始估计值为=2 × 106I3。

通过图9和图10可以观察到航天器的三维追逃轨迹以及两者间相对距离的变化情况，拦截器在经过501 s 的追击后成功地拦截了目标。从仿真图11中可以看出，在估计目标控制矩阵并采取相应的行为学习方法后，拦截器的控制性能与完全信息条件下的情况相对接近，说明在目标信息不完全的情况下，通过信息估计来适配目标的控制矩阵可以有效提高航天器的拦截性能。

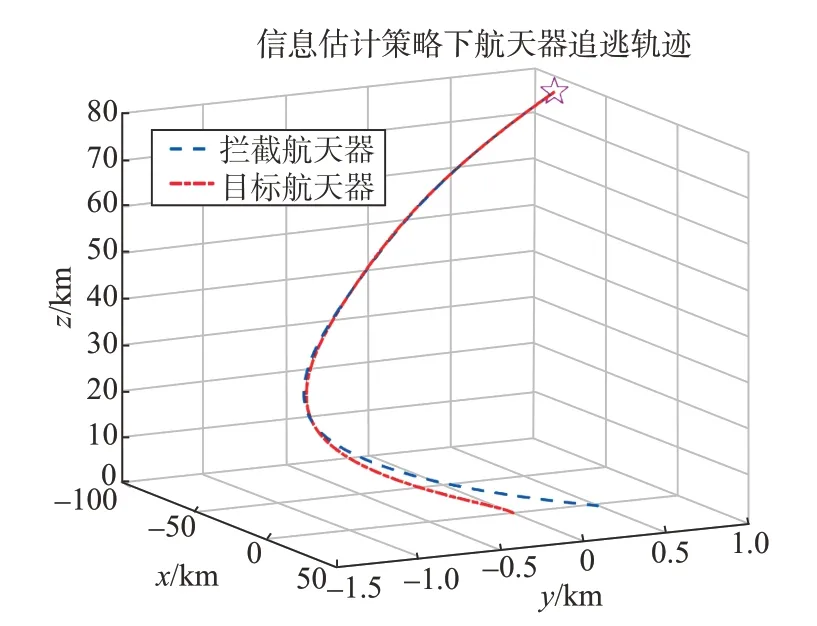
图9 不完全信息估计策略下航天器追逃轨迹Fig.9 Spacecraft pursuit-evasion trajectory under estimation strategy

图10 不完全信息估计策略下航天器相对距离Fig.10 Relative distance of spacecraft under estimation strategy

图11 不完全信息估计策略下拦截器控制加速度Fig.11 Control acceleration of the interceptor under estimation strategy

图12 显示了拦截器对目标控制矩阵信息的估计误差，通过广义Kalman 滤波算法，可以有效地对目标信息进行估计，估计误差快速收敛。

图12 目标信息估计误差Fig.12 Estimation error of the target information

在追逃博弈中，代价函数值是衡量策略优劣的标准。图13 给出了3 种博弈场景的代价函数指标。结果表明，当拦截器采用信息估计策略时，相应的指标明显优于不完全信息方案，拦截时间短、成本低，并且接近完全信息方案的指标，这验证了不完全信息估计博弈策略的有效性。

图13 三种博弈场景的代价函数指标值Fig.13 The cost function values of the three game scenarios

6 结论

本文探讨了在不完全信息的情况下，如何设计一种快速、有效的航天器末端追逃博弈策略。首先，本文基于微分对策理论推导出完全信息下的纳什均衡策略对。为了对未知的目标信息进行估计，进一步提出了基于广义Kalman 滤波的估计算法。在此基础上，设计了不完全信息下的航天器追逃博弈策略，并严格证明了该策略满足ε-纳什均衡条件。最后，通过仿真分析验证了该策略的有效性，结果表明采用本文提出的末端追逃博弈策略可以有效地估计目标信息并实现快速拦截。

综上所述，博弈论与空间飞行器导航、制导与控制相结合具有广阔的应用前景，能够为未来具有自主避障能力的航天器拦截领域研究提供新的思路和方法，有望成为未来空间攻防任务的重要突破点。