大气空间和季节性气候特征对RLV升力式再入飞行的影响
2024-03-17廖雨舟张曙光李静琳王紫扬
杜 涛,廖雨舟,张曙光,程 旋,胡 雄,李静琳,王紫扬
(1.北京宇航系统工程研究所,北京 100076;2.北京航空航天大学交通科学与工程学院,北京 100191;3.中国科学院国家空间科学中心太阳活动与空间天气国家重点实验室/中国科学院空间环境态势感知技术重点实验室,北京 100190)
0 引言
成本低廉、安全可靠的重复使用运输系统(RLV),是航天运输的未来发展方向[1]。航天飞机的飞行成功证明RLV 的工程研制是可行的,但数量级式降低空间进出成本,从而取代一次性运载火箭的初衷并未实现。反因高昂成本黯然退出历史舞台。各国航天届反思基础上投入新方案的探索[2-4]。究其根源在于提升RLV 经济性和可靠性还有大量科学和技术难题需要解决[1]。其中亟待解决的难题之一是RLV 的核心问题——再入飞行同大气间的复杂作用机制[5]。
再入飞行研究长期以静态大气为主,忽视大气动态的复杂性和影响。受对流层活动、太阳辐射和空间天气等因素影响,大气参数表现出空间(高度、经/纬度)和季节性气候特性,以及时间/空间相关的多重尺度复杂变化。大气动态性影响飞行安全评估和边界制定,能够帮助提升在线系统接近极限运行,降低飞行成本[5]。
航天飞机研制[6]和运行[7]上,NASA 提出了高精度大气环境保障要求。研究成果体现在全球参考大气模型(GRAM)的建立和发展[8-9],并应用于X-37B 等项目[10]。GRAM 源于早期卫星和探空火箭等数据的MAP(Middle Atmosphere Program)手册[9],分辨率较低(经/纬度10°×20°,高度5 km)。NASA利用飞行遥测数据等不断改进GRAM[7]。
根据中国航天运输系统发展路线图[11-13],2035年RLV 取代一次性火箭,2045 年实现航班化运输,因此开展RLV 与动态大气相互作用的研究有着现实意义和紧迫性。国内现有的大气模型[14-15],不能满足提升RLV 经济竞争力要求,也无法支撑智能化赋能和信息化驱动的先进性发展要求[13]。
随着大气探测技术的发展,逐步开展了大气扰动建模和影响研究。肖存英等[16]基于TIMED 卫星SABER 载荷探测数据,将大气表征为气候平均值与扰动值叠加模型[17]。程旋等[18]划分扰动为大/小尺度,建立了大气密度参考模型,引入物理约束关系[19]建立全球化临近空间热力学参量模型。刘一博等[20]利用酒泉地区2年探空密度数据与GRAM 比较,在近地高度构建区域参考大气模型。陈闽慷等[21]采用SABER 探测数据,分析了85 km 高度大气参数纬度和季节变化对热环境的影响。程旋等[22]分析了密度月份变化引起的热环境极值分布。
航天飞机采用了升力式(升阻比大于0.7)无动力再入,大气层飞行距离长、跨越经/纬度广,大气气候特征影响显著。本文将基于卫星测量大气数据,采用自研大气建模方法[18-19],提供分辨率优于GRAM 的全域参考大气模型,研究季节性典型月份和空间特征对类航天飞机跟踪再入标准轨道的影响,评估偏离终端目标的特征。
1 全域参考大气模型的建立
1.1 原始大气数据的来源
原始大气数据来自3 颗卫星测量数据。TIMED卫星于2001年12月7日发射,至今在轨运行。轨道高度625 km,倾角74.1°,周期约为1.6 h。搭载SABER 探测器采用临边扫描方式测量大气CO2红外辐射,反演温度和密度等参量。高度范围20~100 km。数据精度参见文献[23]。
Aura 卫星于2004 年7 月15 日发射,至今在轨运行。轨道高度705 km,倾角98.2°,周期约为1.6 h。搭载MLS 探测器采用微波临边探测大气辐射信息,反演大气温度和成分信息。高度范围8~96 km,纬度覆盖范围为±82°N,经度覆盖全球。文献[24]提供了MLS数据的精度分析。
Envisat卫星于2002年3月1日发射,2012年4月8日结束任务。轨道高度796 km,倾角98.54°,平均日轨道数为14.4 圈。搭载MIPAS 探测器临边测量获得大气温度和成分信息。高度范围5~70 km,覆盖全球。文献[25]给出了数据有效性分析。
1.2 数据处理及建模方法
采用文献[16,22]方法对2002—2019年TIMED/SABER,2004—2019 年Aura/MLS 和2002—2012 年Envisat/MIPAS这3颗卫星的观测数据进行垂直插值和水平网格划分,垂直分辨率为1 km,水平分辨率为2.5°×2.5°。在网格划分时,按照月份对每个水平网格内累年的月平均值和标准偏差进行计算,以卫星在网格内的数据量为依据进行加权统计融合。无数据的网格点采用6 阶球谐函数拟合填补,作为模型底层数据。
采用团队自研建模方法[18-19],温度、密度和气压平均值和扰动值之间满足理想气体和静力平衡约束关系,并考虑参量时间和空间相关性。大气周期性大尺度扰动(潮汐波和行星波)以三角函数表征,随机性小尺度扰动(重力波和湍流)采用一阶自回归随机过程表征,方法可靠性验证见文献[18]。后续该大气模型(统称:全域参考大气模型)仿真生成RLV再入轨道上典型月份的大气参数。
2 升力式再入返回任务的制定和制导方法
RLV 完成在轨任务后进入返回程序。升力式返回划分为四个飞行段:离轨、再入、末端能量管理和自动着陆。再入段从进入120 km 高度开始,任务是消耗庞大的初始能量,引导至合适的能量状态和位置范围,进入末端能量管理初始窗口结束。升力式再入制导可分为标称轨道制导和预测-校正制导[26]。本文采用曾应用于美国航天飞机的跟踪标称轨道制导方法[27]。制导方法的不同对大气扰动的适应性有差异,但是不会有质的影响。
2.1 再入任务
以使用升阻比1.1的美国航天飞机公开数据为研究对象[28],选择4 条标准轨道中遭遇最大大气离散事件的高轨道倾角任务[29]。目标落点为我国“神舟”飞船着陆场[30]。据此确定再入端点参数见表1。

表1 再入端点条件和参数要求Table 1 Reentry initial/terminal conditions
2.2 标称轨道设计与跟踪
再入段需满足热流、动压、过载等硬约束[27],与平衡滑翔软约束组成再入走廊如图1所示。标称轨道设计为高度-速度的3次曲线,在再入走廊中取4个参考点,用待定系数法得到预选标称轨道如图1所示。
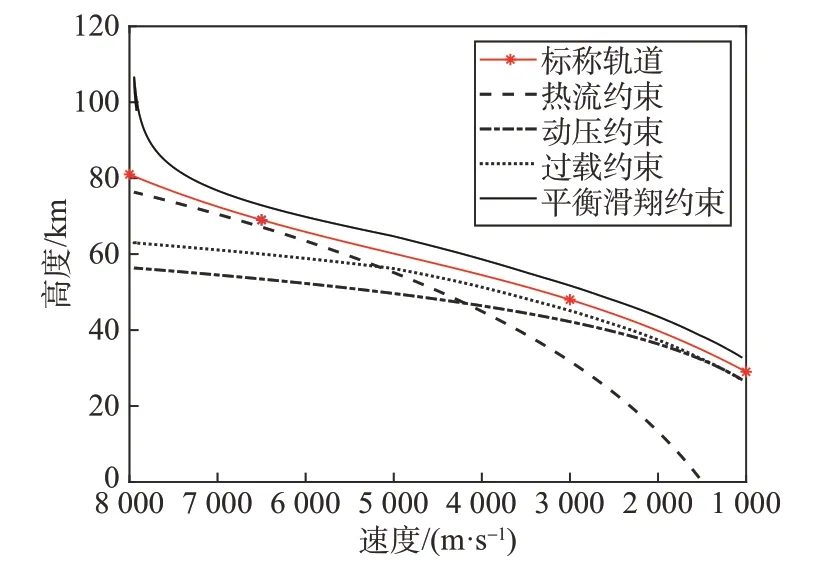
图1 再入走廊与标称轨道Fig.1 Reentry corridor and nominal trajectory
滚转角ϕ是再入过程控制量,调节大小跟踪标称轨道。轨道制导滚转角的控制律:
式中:L为升力;D为阻力;γ为轨道倾角;V为速度;h为仿真模型计算得到(地心距r)高度;href为标称剖面高度;阻尼比ξh和频率ωh为设计参数;m为运载器质量;g为重力加速度。
在与预期落点弧线距离和航向偏离角度过大时,设计滚转角反转逻辑控制航向。大气密度采用美国1976 年标准大气模型[14]。仿真显示RLV 成功到达终端位置,并满足约束要求如图2所示。

图2 标称轨道飞行仿真结果Fig.2 Simulation result of nominal reentry trajectory
3 大气扰动对再入制导特性的影响分析
3.1 标准大气的拉偏模型
评估大气扰动影响目前做法是标准大气拉偏,包络大气偏离。通常假定随高度恒定且随机性符合正态分布:
式中:ρnom(h)为高度h的标准密度;Δ为偏差,满足均值为0、标准差为σ的正态分布。本文取3σ为标准密度的30%。也有文献采用更高的40%[31]。
3.2 全域参考大气模型
3.2.1 全域参考大气模型的生成
由第1节建立的全域参考大气模型提供飞行轨道1 月、4 月、7 月和10 月的密度。轨道上每点密度除受季节、地理经纬度的影响,也受弹道点相互之间在时间/空间上的相关性影响。图3 提供了随机产生的7月1 000条沿轨道的密度曲线在轨道45 km高度点上的频数统计结果,其他高度和季节也类似,为拟正态分布,同GRAM一致[9]。
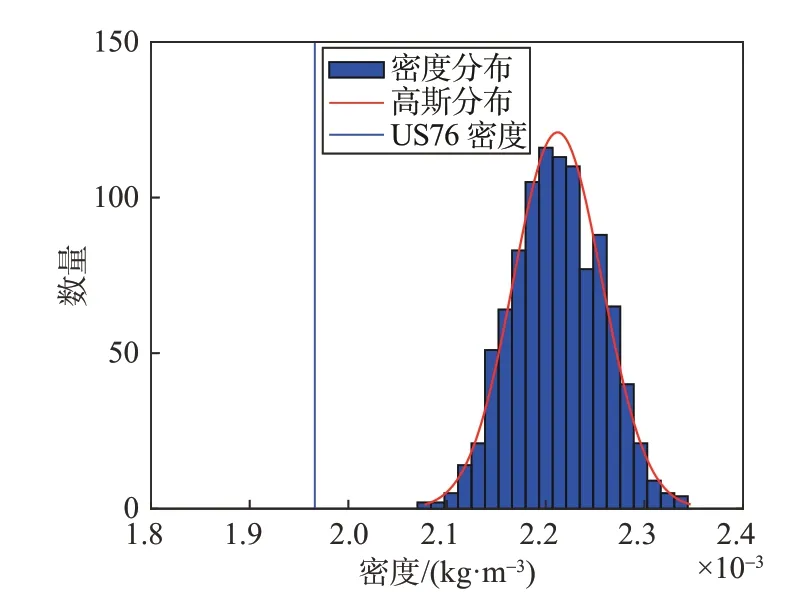
图3 飞行轨道典型高度密度统计分布(7月)Fig.3 Typical height density distribution model for July
3.2.2 全域参考大气模型的特点分析
图4 提供了标称轨道典型高度上4 个典型月份的密度分布,红色虚线的正态分布代表标准大气模型的拉偏模型。60 km 以上参考大气模型的月度散布较大,与拉偏模型较为一致;低于60 km 高度后,月度散布明显出现收窄趋势。

图4 飞行轨道典型高度上各月份全域参考大气模型分布Fig.4 Global reference atmospheric model distribution for each month at the typical altitude of the trajectory
为分析需要,定义月度密度均值偏差Δ(h):
式中:ρmean(h)为高度h上月度平均大气密度;ρnom(h)为该高度上的标准大气密度。
定义密度的月度相对标准偏差rσ(h)如下:
式中:σ(h)为高度h上月度大气密度的标准偏差。
图5 提供了大气密度月度均值偏差Δ(h)随轨道高度变化。夏季7月变化复杂,同其他月份不同。最大负偏差出现在100 km 高度(-58%),之后随高度降低快速单调增加;在77 km 高度出现最大正偏差+58%,之后随高度下降向标准大气回归。相反,1 月、4 月和10 月密度均值偏差整体为负偏差。4 月密度偏差最小,接近标准大气模型。1月和10月分布高度一致,峰值同样出现在77 km 高度上,接近-40%,之后随高度下降向标准大气回归。低于50 km高度后同标准大气无显著差异。
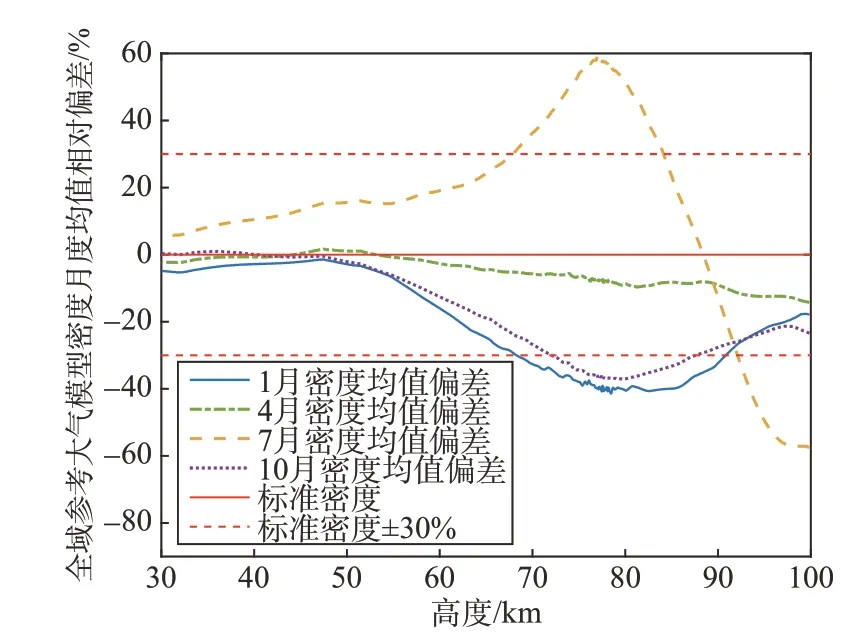
图5 全域参考大气模型密度月度均值相对偏差Fig.5 Relative deviation of monthly mean density in global reference atmospheric model
图6提供沿标称轨道高度的大气密度相对标准偏差rσ(h),表征分散度。rσ(h)在90 km高度有明显趋势反转。90 km 之上7 月的偏差最为剧烈,其他3个月份规律较为一致。低于90 km 后,冬季1 月的离散度最大,达到15%,反而夏季7 月离散度最小,低于5%。4 月和10 月的大气离散度高度一致。简单概括,春季的均值最接近标准大气模型,夏季均值偏离标准大气最严重。冬季大气离散度最大,夏季离散度最小。大气这种复杂气候特性是标准大气拉偏无法提供的。
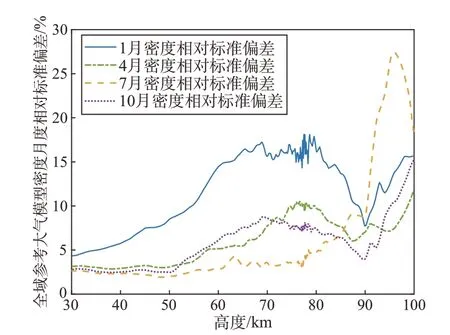
图6 全域参考大气模型密度月度相对标准偏差Fig.6 Monthly relative standard deviation of density in global reference atmospheric model
文献[32]提供了GRAM 模拟航天飞机104°倾角再入任务1 月和7 月密度,与本文趋势基本一致,区别在于1 月密度在100 km 高度从正偏差向负偏差穿越,7 月扰动更大。这可能体现经度不同的影响。
3.2.3 全域参考大气模型的大气动力学分析
标准大气模型表征北半球中纬度地区在中等太阳活动条件下的理想化平均大气状态,而全域参考大气模型表征更为复杂的大气动力学动态特性。平流层高度(20~50 km)由于大气臭氧对太阳紫外辐射的吸收加热作用,温度升高,温度梯度由夏季极区指向冬季极区;在大气重力波上传饱和破碎过程中,形成由夏季半球向冬季半球流动的全球经向环流,导致平流层和中间层(50~85 km)夏季大气密度高于冬季,并随纬度增加而增加。在中间层顶区域(80~100 km),由于上传大气重力波的破碎和冷却作用,温度梯度反转,由冬季半球指向夏季半球。春秋季节则是冬季和夏季的转换季节。
观察图2再入轨道,50 km以上轨道在高纬度地区(60°N~90°N),50 km 以下轨道处于中纬度地区(40°N~60°N)。这种纬度的差异,是图5中在50 km以上全域参考大气模型严重偏离标准大气模型的原因。图7 给出了1 月和7 月大气密度与标准大气模型偏差随纬度、高度的变化特性,图中白色实线为轨道线。

图7 北半球纬圈平均密度相对偏差随纬度和高度的分布Fig.7 Distribution of the relative deviation of the mean density of the northern latitudes with latitude and altitude
偏离大气月平均密度的散布受大气潮汐、行星波和重力波等因素影响。定义大气密度扰动相对标准偏差r(h,φ)(φ为纬度)为标准偏差σ(h,φ)相对于纬圈月平均值ρmean(h,φ)的百分比:
图8提供了1月和7月大气密度相对标准偏差随高度和纬度的分布特征。在低热层(90~100 km),大气波动常年较强,夏季大于冬季,主要贡献来自于大气重力波活动,其次是传播性行星波和大气潮汐[16]。在1月份中间层顶附近存在静态行星波的临界层,导致静态行星波被吸收、反射和折射[33]。在高纬平流层和中间层(20~80 km),冬季1 月份大气密度相对标准偏差较大,主要是由于北半球冬季强烈的行星波和重力波活动上传引起[34]。

图8 北半球大气密度相对标准偏差随纬度和高度的分布Fig.8 Distribution of the relative standard deviation of atmospheric density in the northern Hemisphere with latitude and altitude
夏季7月份,该高度大气密度相对标准差较小,一方面是因为平流层20 km 附近存在准零风层,阻挡了地形激发的重力波上传,另一方面,夏季平流层纬向背景为东风,而非大尺度静态行星波上传的弱西风条件,导致扰动较弱。
3.3 大气扰动特性对再入影响的分析
按照大气的分布特征,开展100 次随机密度仿真。通过结果的散布情况,研究大气的分布特性对再入的影响,及是否满足走廊约束和终端偏差约束。
3.3.1 拉偏仿真统计结果
表2 给出了拉偏仿真结果的统计,86%能满足终端要求,88%满足轨道约束,有82%能同时满足两者,成功返回。终端散布结果给出在3.3.3节。

表2 全域参考大气模型密度仿真结果统计Table 2 Statistics of density simulation results in global reference atmospheric model
3.3.2 月度平均密度仿真结果
首先开展了月度平均密度跟踪仿真(图9和表2)。仅有4 月份能够满足轨道约束和终端约束,其余月份均存在终端位置出圈。

图9 月度平均密度再入仿真控制量Fig.9 Control value with monthly mean density in reentry simulation
可以预测飞行高度降低、动压增大后,大气偏差对飞行影响才会显现。采用代表能量的速度偏差监测大气偏差的影响(图10),仿真结果显示在80 km 才开始显现月度差异。因此RLV 再入任务只需关注80 km高度以下的大气偏差。
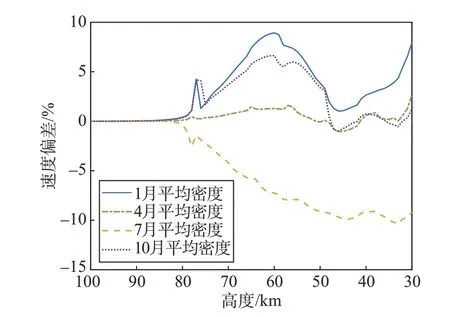
图10 月度平均仿真随高度的速度偏差Fig.10 Monthly average simulation velocity deviation with altitude
另一个值得注意的现象是,1 月和10 月的平均密度为负偏差,通过增加滚转如图9 所示,60 km 高度以后出现了速度偏差的修复,而7 月密度正偏差引起的速度负偏差代表能量耗损过大(见图9),无法修复,呈现持续性放大。
3.3.3 全域大气模型仿真统计结果
全域参考大气模型提供每月份100条沿轨道大气密度,开展RLV 再入跟踪标准轨道仿真。飞行器终端位置和速度统计提供在表2中。首先观察图11中仿真飞行器终端位置分布。1月和10月的终端位置分布高度重合:全部超过目标落点位置范围,最近落点水平距离554 km。这与两个月份大气密度较高相似度的负偏差特性相关。易超出轨道刚性约束,尤其离散性最大的1月。

图11 全域参考大气模型密度月度仿真落点分布Fig.11 Density monthly simulation drop point distribution in global reference atmospheric model
7 月大气密度正偏离标准大气模型,仿真表现为无法抵达标准落点且距离较远。加之离散度最低,终端位置和速度分布集中,且基本能满足轨道刚性约束。4 月大气密度仿真分布最接近标准密度模型仿真,大部分落点位置在目标位置范围内,整体上水平距离偏差较小,落点速度稍偏大。
作为对比的拉偏分析的终端位置,基本分布在要求范围内,呈“之”字形分布。这是因为调整滚转角是制导律调整能量、跟踪标称能量剖面的方法。当大气密度偏低气动耗能少时,会增大滚转角转弯消耗多余能量,呈现飞过目标后的南侧落点东西分散分布。反之能量不足则避免转弯,呈现飞不到目标位置北侧落点直线分布。“之”字形分布反映了上述两类情况同时存在。
图11中标注了终端速度超条件的工况,发现仅有拉偏模型存在终端速度超条件。进一步分析,将终端速度和距离偏差绘制成相图(见图12)。4月大气模型下终端速度和位置均跟踪良好。1月、7月和10月终端位置不满足要求,但终端速度均满足要求。整体上7 月速度偏小,1 月速度偏高,4 月和10 月居中。而拉偏仿真虽然终端位置偏离较低,但终端速度偏离严重,分布在广域范围。两类模型的终端偏差表现大相径庭。原因在于全域参考大气模型在较低高度上偏差减小,接近标准大气模型,制导律持续修正下,飞行容易最终跟上标称能量。而拉偏模型全程相同比例偏差,再入飞行难以跟上标称能量,夸大终端能量偏差。

图12 终端速度-位置偏差分布Fig.12 Distribution of terminal speed versus position deviation
再入飞行段不同指标超差的严重性不是平等的,由大到小依次是:过程约束不满足、终端能量(速度)不满足、终端位置不满足。第一项是刚性约束,导致不可逆的结构/防热系统受损。后两项危害是增加后续制导负担,并非刚性,当然严重也可能着陆时都无法修正。
工程研制上采用拉偏分析的初衷是通过覆盖大气的偏差范围,从而覆盖真实大气对再入飞行的影响。上述仿真显示这一初衷并未实现。拉偏仿真的超差表现为终端位置良好,终端速度严重偏离,而月度大气模型仿真表现完全相反。这里进一步提供一个例子,取4月平均密度和任一条4月随机密度,并与标准大气模型的-6%拉偏仿真进行对比。拉偏模型几乎可以覆盖80 km 高度以下的随机模型和4 月平均密度模型(见图13),但仿真结果终端速度能够覆盖,位置偏差不能覆盖,前者是61.03 km,随机模型是96.52 km。随机密度仿真结果更接近当月平均密度的位置偏差120.61 km。
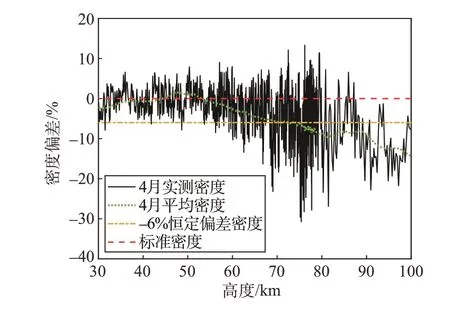
图13 恒定偏差与实测大气密度偏差Fig.13 Constant and measured atmospheric density deviation
拉偏仿真并不能覆盖真实大气偏差给升力式RLV 再入仿真的影响,这会误导后续RLV 适应性改进和优化方向,给设计工作带来不必要负担。因此RLV 设计中引入参考大气模型,对提升性能和适应性有着不可替代的作用,这也是美国航天飞机研制中使用GRAM而非拉偏模型的原因[32]。
4 结论
本文采用自建全域大气参考模型,探讨了大气密度空间和季节性气候变化对跟踪类航天飞机的升力式RLV再入返回任务的影响,得到如下结论:
1)大气月度密度表现为受空间和季节相关的大气动力学影响,80 km 以下大气密度的偏离对RLV再入飞行会产生影响。
2)大气密度同轨道空间性和季节性相关的偏差特性和散布特性会强烈影响RLV 飞行跟踪标准轨道,终端分布特征表现出季节性特征。
3)通过覆盖大气偏差范围的拉偏并不能覆盖月度大气的真实仿真行为。引入参考大气模型对提升RLV性能和降低成本有着积极作用。
