汇流排型材在重力作用下最大挠度与其截面参数关系探讨

张学明，王春娟，严仁杰，畅 明，豆 雯

0 引言

电气化铁路刚性悬挂接触网汇流排是刚性接触网中用于夹持固定接触线，并靠其自身的刚性保持接触线的恒定位置，使接触线不因重力而产生弛度的部件[1-3]。刚性接触网中所用的汇流排一般由铝合金制成，其质量检验所依据的行业标准为TB/T 3252—2022。在该标准的出厂试验项目中，对汇流排型材有最大挠度方面的要求。一般而言，型材的最大挠度与材料弹性模量、截面形状、型材长度、所受弯矩等因素有关。下文将通过求解型材的挠度曲线方程，讨论该类型材最大挠度的影响因素及其控制方法。

1 建立力学模型

一般而言，如果对型材在重力作用下有挠度要求，往往会规定一个合适的跨距，在该跨距内，型材相应位置的挠度应满足一定要求。为方便描述，绘制如图1 所示力学模型，并在图1 中建立直角坐标系xow，设型材长度为l，用于检测挠度的2 个支撑点位置分别设为（l1，0）和（l2，0），型材单位长度质量为m，则支撑点间距（跨距）为l2-l1，单位长度的重力为mg（g为重力加速度，其值为9.8 m/s2）。

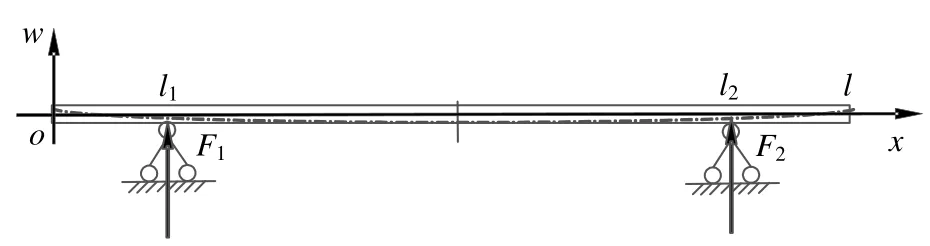
图1 力学模型

由静力学平衡条件可知：

对于支点关于中轴线对称分布的情况，有l=l1+l2，此时式（1）、式（2）可化简为

式（1）、式（2）比式（3）更具一般性，但用其推导出的方程十分复杂，且在型材挠度测量中一般不使用该方程，故本文不作讨论，如遇到此类情况，可直接求出F1和F2的具体数值，并用下文所述方法代入求解即可。本文只讨论式（3）的情况。

根据图1 所建立的直角坐标系及式（3），由端面法易知剪力方程为

需注意的是，支撑点处有集中力F1、F2，剪力方程不连续。

由材料力学可知，弯矩与剪力有如下关系：

将式（4）代入式（5），并由图1 可知，无集中力偶作用时弯矩不发生突变，为连续函数，且M(0) =M(l) = 0，故弯矩方程为

2 求解挠曲线方程

根据材料力学知识，挠曲线近似微分方程为[4]

式中：w为挠度；E为弹性模量（又称杨氏模量）；I为截面对中性面的惯性矩。

对式（7）进行一次积分，可得转角方程为

将式（6）代入式（8），转角方程为

对式（7）进行二次积分，可得挠度方程为

将式（6）代入式（10），可得

根据图1 及挠度光滑连续条件得边界条件为

将式（12）代入式（9）及式（11），并由挠度光滑连续条件可得积分常数为

3 问题讨论

依据TB/T 3252—2022 的第6.8 条，刚性悬挂接触网汇流排的挠度测量方法为：在专用平台上用4 个特制的可调高度的锥形垫脚将12 m 汇流排垫起，汇流排两端各用2 个锥形垫脚；锥形垫脚的支点距离型材端头50 mm，调节4 个垫脚水平，用高度游标卡尺量得型材两端最大高度与汇流排中部最小高度的差值[5]。根据该标准要求，可确定l1= 50 mm，l2= 11 950 mm，l= 12 000 mm；再根据汇流排截面形状及尺寸，利用CAD 软件计算其截面对中性面（即xoy面，其中x轴过o点且垂直于截面）的惯性矩I= 3 403 543.47 mm4。汇流排截面如图2所示。

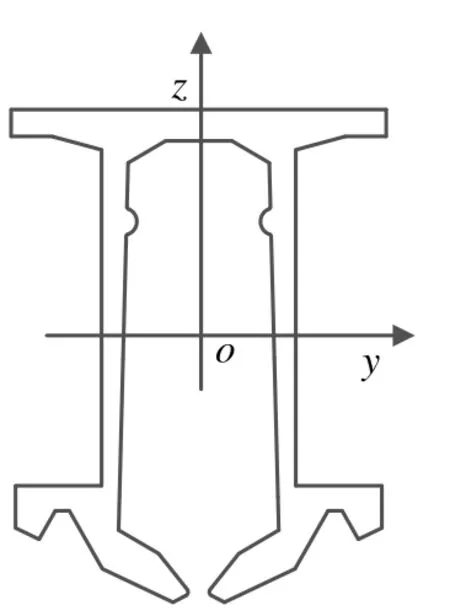
图2 汇流排截面

需注意的是，利用CAD 软件计算截面惯性矩时，不能直接求解，须先确定型材截面的形心，并将系统坐标系原点设置于型材截面的形心处。图2中yoz坐标系原点o即为汇流排型材截面的形心。

经计算可以得到型材的截面积A= 2 235.02 mm2。一般电气化铁路刚性悬挂接触网所用汇流排为6101B（T6）铝合金，在室温下其对应的弹性模量为69 000 N/mm2。考虑到其密度约为2.7 g/cm3，则该截面的汇流排单位长度质量m= 2.7×10-3×2 235.02 g/mm = 6.03 g/mm = 6.03 kg/m。

综上所述，式（11）中涉及的所有参数均可计算得到，如表1 所示。

表1 汇流排挠度方程参数

将表1 中的数据代入式（11），可得汇流排在TB/T 3252—2022 第6.8 条要求下试验时的挠度方程为

图3 汇流排挠度曲线（单位：mm）

以上挠度方程及挠度曲线是根据理论计算得出的，表2 是对10 根不同批次、规格为12 m、截面为图2 所示的汇流排，严格依据TB/T 3252—2022 的第6.8 条要求测量的最大挠度实测值。

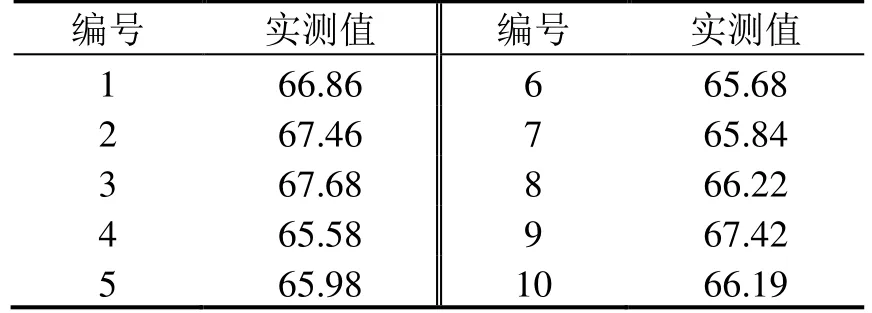
表2 汇流排挠度实测值 mm

结合理论计算结果，从表2 可以看出，汇流排最大挠度的实测值与理论值相差不大。查阅相关资料可知，材料的弹性模量是材料抵抗弹性变形的一个量，是材料刚度的一个指标，其与材料的化学成分和温度有关，与组织变化无关，热处理对其影响不大，约为±5%左右[6]。从式（11）可以看出，型材在重力作用下的挠度与弹性模量成反比关系，考虑到热处理对弹性模量的微小影响，汇流排的理论最大挠度范围区间为(66.58×95%, 66.58×105%) =(63.25, 69.91)，而TB/T 3252—2022 的表2 汇流排性能参数中要求最大挠度wmax≤70 mm，若考虑到型材加工误差等其他因素的影响，有可能会导致汇流排型材的挠度不能满足不大于70 mm 的要求。从式（11）可以看出，在型材材质一定、检测方式一定（即型材长度、支撑点位置一定），并考虑到热处理对弹性模量有±5%影响后，影响型材最大挠度的因素只有截面惯性矩和单位长度质量。

下文讨论能否通过增加截面积的方法减小型材在重力作用下最大挠度。增加型材截面积意味着型材单位长度质量m也随之增加，从式（11）可以看出，最大挠度与m和I的比值成正比，而m=ρA，ρ为型材体密度，A为截面积。因此，最大挠度与A和I的比值成正比，即

式中：α为引入的比例系数，mm3；积分区域为型材截面轮廓围成的区域。对于不同的截面形状，A/I一般也不同，当增加截面积时，若A/I随之增大，则无法通过该方式减小型材在重力作用下的最大挠度，若A/I随之减小，则可以通过该方式减小型材在重力作用下的最大挠度。但是，通过这种方式调整型材自重下的最大挠度时，由于A和I均增大，型材挠度的理论值减小效果并不明显，同时也会增大型材单位长度的重量，经济性较差。

综上所述，减小型材在自重作用下最大挠度比较合理的方案是：在满足载荷和安装要求的情况下，保证型材截面积不增加（即保持不变或减小），同时使型材截面的材料尽量远离中性面，以增大型材对中性面的惯性矩I。

以图2 为例，TB/T 3252—2022 第5.2.2 条规定了钳口尺寸，这是用于夹持接触线的关键尺寸，不能随意变更。对除此之外的其余尺寸，在不影响现场安装并满足载荷要求的情况下，可以尽量使之远离xoy平面。如果不考虑其他因素，对图2 汇流排截面的顶部尺寸增加1 mm，同时各壁厚保持不变，此时，计算型材截面的截面积及惯性矩分别为A=2 210.93 mm2，I= 3 417 492.22 mm4，与图2 相比，截面积有所减小，惯性矩有所增加。此时m=ρA=5.97 kg/m。将I及m代入式（11），并利用表1 的其他数据，可计算出w(x)m=w(6 000) = -64.70 mm，w(0) =w(12 000) = 0.87 mm。最大挠度wmax=w(0)-w(x)m= 65.57 mm。考虑到热处理对E有±5%的影响，此时，汇流排的理论最大挠度范围区间为(62.29, 68.84)，即使考虑制造误差，挠度的理论值仍有一定的裕度，可以满足TB/T 3252—2022 表2中最大挠度不大于70 mm 的要求。

对于有挠度要求的型材，理论上可根据式（17）确定其截面几何参数。例如，型材在某段距离支撑点下的最大挠度应满足wm≤[w]，[w]为允许最大挠度，即

式中：α为引入的比例系数，mm3。从式（11）可以确定只要型材的材质一定（即E、ρ一定），挠度的测量条件一定（即l、l1、C2、D2一定），则α即为定值。式（19）可作为满足型材挠度要求的充分必要条件。对于截面形状规则的型材而言，可以通过式（19）准确计算出其截面尺寸的临界值，如为圆形截面，可以求出最小直径。但对于形状不规则的截面，由于（截面坐标系为yoz，原点为截面形心），积分区域为型材截面轮廓围成的区域，很难通过函数关系准确表达，一般无法找到截面尺寸需要满足的临界条件，但可以借助软件求解A/I的具体数值，然后代入式（19），反向验证设计的截面尺寸是否满足挠度要求。

4 结语

型材在重力作用下的挠度是表征型材抵抗弯曲变形的重要指标，通过分析可知，若考虑热处理对材料弹性模量的影响，本文所述截面形式的汇流排通过理论计算出的挠度值非常接近标准值。对于此类情况，建议在不增加截面积的前提下，可以适当改变型材材料的分布情况。本文推导出的挠曲线方程可用于一般型材在重力作用下最大挠度的校验，也可用于确定某些形状规则简单截面的临界尺寸。对于有热处理要求的型材，如果技术标准中或实际工况中对型材挠度的控制要求较高，设计型材截面时还应考虑5%的弹性模量变化。