重大突发事件下应急物资分配优化模型

相晨宇，刘 宁

（沈阳建筑大学 管理学院，辽宁 沈阳 110168）

0 引言

重大突发事件一般指突然发生、造成或者可能造成严重社会危害,需要采取应急处置措施予以应对的自然灾害、事故灾难、公共卫生及社会安全事件，具有偶然性、危害性、紧急性和影响大等特点[1]。我国在控制、减轻和消除突发事件引起的严重社会危害上制定了多项措施，其中，应急物资的保障工作是战胜突发事件的重要环节，物资的合理分配更是至关重要。在重大突发事件期间，应急物资的需求不仅由突发事件的发展程度决定，还受公众的心理行为影响，物资供应呈现出需求难以预测、市场主导的供给机制失灵以及供需信息不对称等问题[2]。任何重大突发事件都会对相关人员的生活和工作产生较大的影响，因此，实现物资的合理分配是稳住人们心态的关键。

重大突发事件下的物资分配供应问题一直是众多学者关注的研究热点，在突发事件初期对及时支援、救助病患和防止扩散的问题上，大多研究倾向于在最短的时间内将物资运达指定地点，缓解重大突发事件带来的物资紧缺问题。

一类研究主要集中在供需平衡上，杜丽敬，等[2]主要从考虑物资供应与疫情演化耦合关系的需求预测、完善疫情演变下医疗物资转扩产产能调节机制和搭建基于互联网的社会捐赠医疗物资供需平台等方面解决物资供应问题；王付宇，等[3]利用SEIR预测决策时刻各灾区感染人数，由此计算灾区紧迫程度权重与物资需求量；吴涵，等[4]通过K-means聚类分析提出了医药物资筹措全过程分阶段、分重点的可持续优化策略；胡忠君，等[5]通过构建结合“互联网+”的研究框架,提出了一种混合优化方法实现灾区需求预设满足程度。

另一类研究主要集中在高效率上，一些学者对多目标路径优化问题，设计出了改进的多目标蚁群算法。王新平，等[6]采用纵向配送和横向转运相结合的协同配送模式,构建了一类应急物流网络优化多目标随机规划模型；庄媛媛，等[7]通过SEIR模型预测应急物资需求，以应急物资需求缺货损失最小与物资分配总距离最短为目标构建了优化模型；黄辉，等[8]从救援物资的高效投放出发研究了最优车辆调度决策问题；蔡延光，等[9]针对应急物流中的运输时效性和物资分配公平性，提出了一种两阶段应急物流运输与物资二次分配策略；杨勃，等[10]提出一类具有多个受灾点、多种救灾物资的分配调度问题，实现所有受灾点物资需求时间最短。

应急物资分配是否合理在解决哄抬物价、囤货居奇行为的同时也能大大缓解公众的恐慌心理。因此，根据重大突发事件的特点，物资发放不合理可能会导致影响进一步扩散，在判断物资发放是否合理时，受影响人数是一个重要指标。这里的受影响者是指灾害事件遇难及受伤人数和公共卫生事件感染及死亡人数等。判断物资发放是否合理并且对发放点数量进行优化是本文研究的主要问题。

1 基于GM(1,1)预测与熵权法的应急物资分配模型

1.1 灰色预测模型

灰色预测模型是通过少量的、不完全的信息，建立数学模型并做出预测的一种方法。当我们运用运筹学的思想方法解决实际问题，制定发展战略和政策、进行物资发放等问题的决策时，都必须对未来进行科学的预测。灰色预测理论是研究灰色系统分析、建模、预测、决策和控制的理论。灰色预测模型所需建模信息少、运算方便、建模精度高[11]。将已获取的重大突发事件地区信息完全确定的受影响者的数量作为白色系统，在假设未发放应急物资的情况下，将突发事件地区信息完全未确定的受影响者的数量作为黑色系统，通过GM(1，1)对未确定的受影响者的数量进行预测建模[12]。

式（3）中：a表示发展系数，表征预测对象的发展状态；b为灰色预测中的灰色作用量，表征数据变化的关系。

通过最小二乘法求得方程的解为：

最后通过累加生成算子逆变换得到方程：

式（6）中：

1.2 后验差检验

为了验证GM（1，1）模型对于新增受影响者的数量预测结果是否准确、可靠，通过后验差方法对模型精度进行检验。

式中：

1.3 熵权法评价模型

通过建立熵权法评价模型对投放点数量的合理性进行分析。熵权法评价模型具有客观性、适应性等特点[13]。

熵权法评价模型中的信息熵求解公式为：

其中i为影响因素指标；Pij表示每项指标数值占总数的比例；n指分组数量；H介于0到1之间。

计算出各个指标的熵值后，再根据第i个指标的熵值计算熵权。

综合GM(1,1)灰色预测法、后验差检验和熵值法构建重大突发事件下应急物资分配优化模型。

2 算例分析

2.1 针对长春市疫情的GM（1，1）预测分析

通过分析发放应急物资（蔬菜包）前后长春市各个区的新增感染者人数，将这些新增感染者人数数据以折线图的形式表现出来，分析折线图的变化趋势，以此判定发放物资对控制疫情发展是否有影响。因仅有发放物资后的新增感染者人数，无法进行对照试验，因此需要采用灰色预测法[14]进行预测拟合分析，预测不发放物资的新增感染者人数，再利用控制变量法对比分析长春市发放物资前后效果。

对长春市疫情期间各个区以及全市汇总的新增本土感染者与新增无症状感染者进行统计，绘制出长春市疫情期间新增感染者人数折线图。以2022年3月14日作为第1周，以九台区、绿园区、朝阳区、经开区、宽城区、南关区和二道区这些新增感染者人数较为显著的7个区为例，得到长春市疫情期间新增感染人数折线图，如图1所示。

图1 长春市疫情期间新增感染人数折线图

由图1可知，长春市疫情期间新增感染人数的变化趋势为先增后减，在2022年4月2日时达到新增感染人数最大值后新增感染者人数开始下降。考虑到新型冠状病毒的潜伏期大约在7天左右[15]，恰好是长春各个区自2022年3月26日陆续开始发放物资后的第7天，说明物资的发放对抑制疫情的发展有良好的作用。

以2022年3月4日到3月26日这23天信息完全确定的新增已确诊和无症状感染者人数作为白色系统，在假设未发放应急物资（蔬菜包）的情况下，将3月27日到4月14日这19天信息完全未确定的新增确诊与无症状感染者的数量作为黑色系统，通过GM(1，1)对未确定的新增感染者人数进行建模预测。

为了使结论更加可靠，分析模型对于新增感染者人数预测结果是否准确、可靠，可通过后验差方法对模型精度进行检验，后验差精度标准见表1。

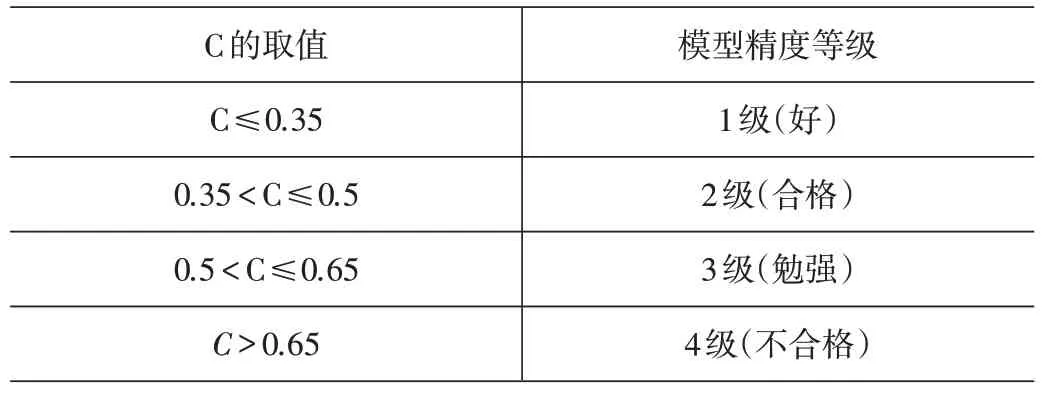
表1 后验差精度标准

基于2022年3月4日到3月26日的新增感染者人数数据，采用GM（1，1）灰色预测未发放物资情况下3月27日到4月14日的新增感染者人数。首先预测出2022年3月27日、3月28日新增感染者人数，求得方差为0.64，由表1可知，模型精度为勉强，可以应用。利用预测得到的3月29日、3月30日新增感染者人数，预测3月31日、4月1日新增感染者人数，同理得到长春市十六个县区2022年3月27日到4月14日新增感染者人数的预测结果，见表2。

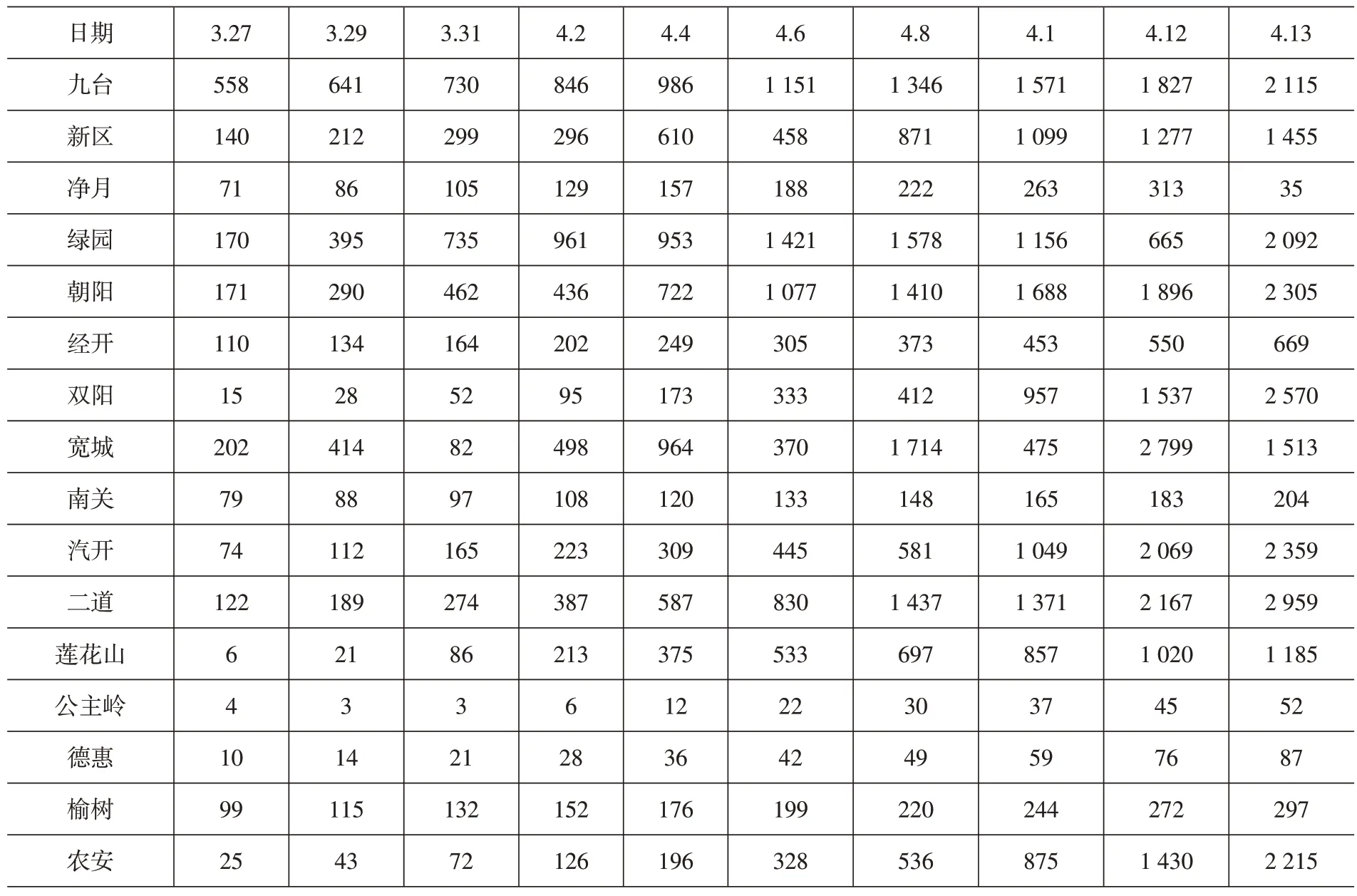
表2 长春市疫情期间新增感染者人数预测表

以2022年3月14日作为分析的第1天，对长春市实际总计新增感染者人数和未发放蔬菜包情况下预计新增感染者人数进行对比，结果如图2所示。由图2可以看出，蔬菜包的发放对抑制疫情的发展的确有良好的作用。

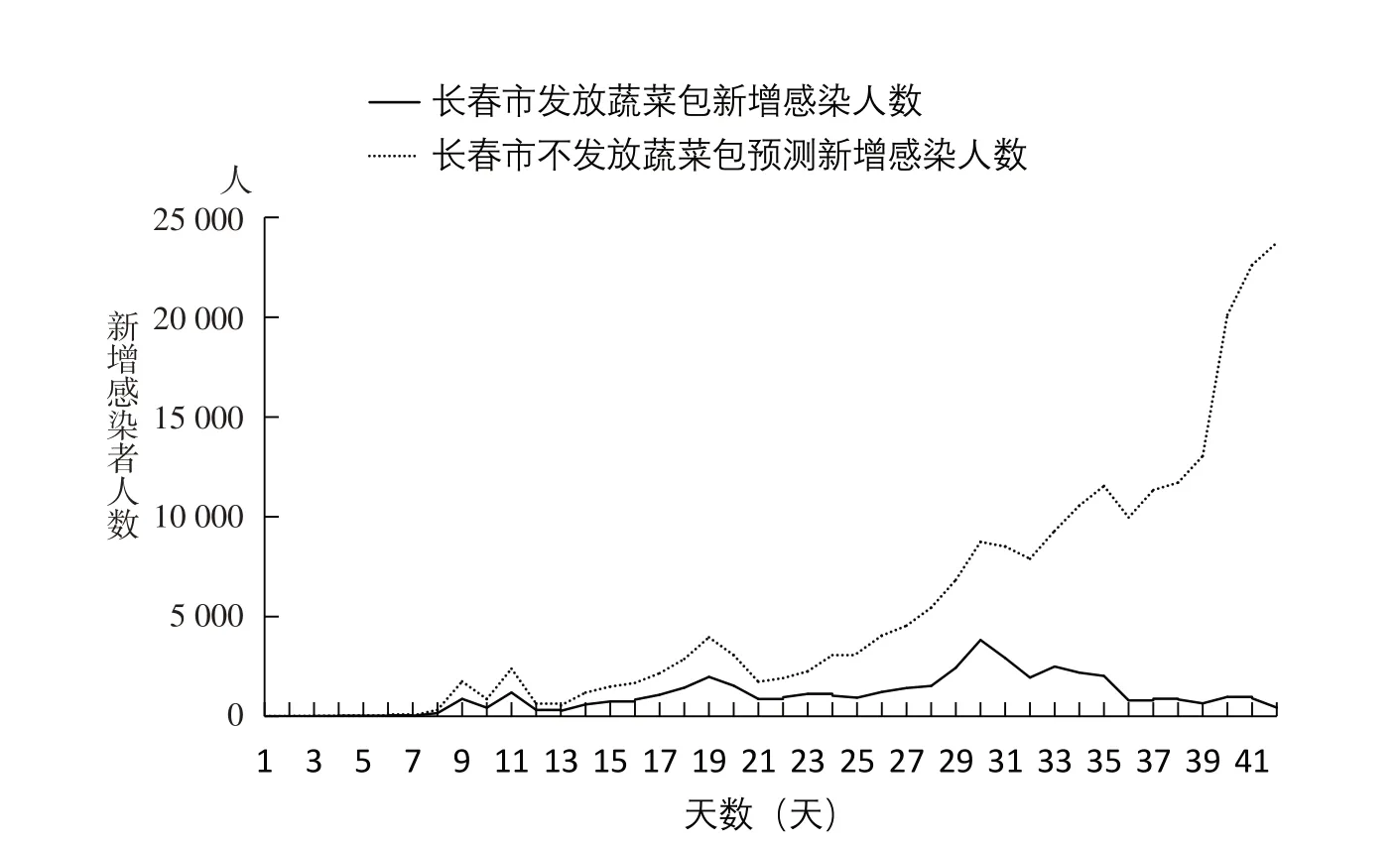
图2 长春市发放蔬菜包与不发放蔬菜包新增感染人数折线图

2.2 基于熵权法的蔬菜包数量合理性分析与优化

结合长春市九个区主要小区的数据，将小区栋数、小区户数、小区人口数、街道数目以及新增感染者人数作为评价指标体系的因素集，以长春市九个区为评价打分对象，采用熵权法对长春市不同区域投放点数量进行合理性分析和权重分配，确定合理的投放点数量。长春市九个区各个因素所占比例见表3。

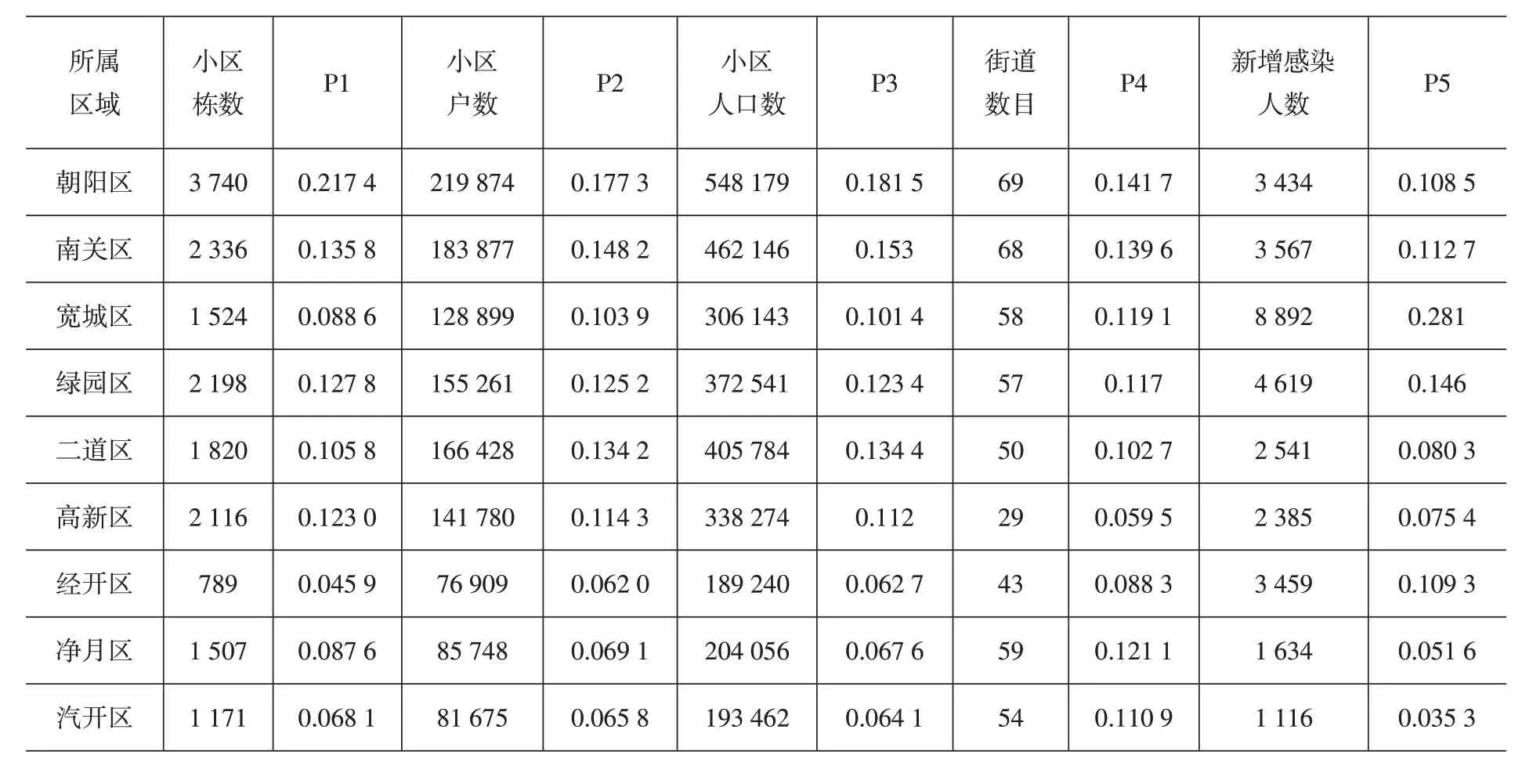
表3 长春市九个区研究指标汇总及概率表

用i表示小区栋数、小区户数、小区人口数、街道数目以及新增感染者人数这5个指标；Pij表示每项指标数值占总数的比例；n=9；H介于0到1之间。基于式（11）、式（12）计算得到5个指标的熵值与熵权见表4。

表4 五项指标的熵值与熵权表

利用表4中的熵权求出各个区的值记为得分，根据得分求出各个区的投放点系数占比，对物资投放点进行重新分配，结果见表5。

表5 长春市九个区投放点系数及重新分配表

根据上述分析可知，各个区的投放点数量不合理，优化后各个区的投放点数量为：朝阳区279个，南关区235个，宽城区164个，绿园区193个，二道区207个，长春新区（高新）174个，经开区98个，净月区105个，汽开区100个。

通过分析长春市疫情期间应急物资发放情况与投放点数量优化，可以发现在重大突发事件中，应急物资合理发放的确有助于降低突发事件给人们生活和工作带来的影响，极大地降低了其所造成的损失。

3 结语

本文以长春市为例，围绕其应急物资发放的合理性，对应急物资发放点数量进行优化，这是对现有重大突发事件物资分配合理性研究的有力补充，同时也能为发生重大突发事件时优化应急物资分配点数量提供必要的参考依据。

研究结果主要揭示两点：一是合理发放应急物资是缓解重大突发事件的有效措施；二是优化发放点数量是提高应急物资合理分配的关键因素。未来将进一步考虑各个应急物资供应点间的距离，建立距离最优模型，寻找最优的应急物资投放点，进行选址优化，进而确保应急物资发放的速度。

与已有研究成果相比，本文利用GM（1，1）预测方法对数据进行对比分析，再结合熵权法评价模型优化应急物资发放点数量。该方法也适用于分析其他突发事件下应急物资分配数量的合理性并对其进行优化，如地震、洪灾、其他传染性疾病等。