基于Kriging模型的造纸法再造烟叶筛分工艺参数优化方法

李锦,罗冲,闫瑛,马建荣,李高辉

1.河南卷烟工业烟草薄片有限公司,河南 许昌 461000;

2.郑州轻工业大学 机电工程学院,河南 郑州 450002

0 引言

再造烟叶(Reconstituted Tobacco Sheet,RTS)是将碎烟叶、烟末、烟梗等原料,通过工艺成型、重组而成的薄片状烟草制品[1]。再造烟叶以烟草为原料,加工过程属于物理变化[2],其物质基础与天然烟叶相同,但物理结构更疏松,燃烧性更好,且焦油含量更低[3-4]。因此,在卷烟中掺入一定比例的再造烟叶可以减少对人体和环境的危害[5],且能够提高再造烟叶利用率、减少烟草原料消耗,具有显著的社会效益[6-7]。

再造烟叶技术主要包括辊压法、稠浆法和造纸法。其中,造纸法将烟草生产中的废料重新加工,经过废料处理、纸浆制备、纸张生产等步骤,将烟草废料转化为可用于香烟、雪茄和烟斗制造的再造烟叶产品。造纸法再造烟叶能够避免辊压法中出现的烟叶物理强度低、填充性能差、烟叶表面白色斑点多及稠浆法中出现的生产过程复杂、投资规模大、生产成本高等缺点[8-10],在烟草生产废料的利用方面具有较大优越性。制浆和筛分是造纸法生产再造烟叶的关键工序,其中纤维筛分是将制浆后经过稀释的烟浆悬浮液依次通过多个具有不同尺寸筛孔的筛网,小而短的纤维直接流入下一级,而较大的纤维则被阻留在筛板上[11]。上述工序中,水流速度和烟浆固含量起着关键作用,不仅会影响筛分效率,还会影响不同目数烟末颗粒纤维的质量占比。烟末粒径会影响烟草基片的松厚度和抗张强度,较小的烟末粒径能够提供更好的吸附性能,且增加基片的紧密性,提高烟草基片的抗张强度。然而,过高的抗张强度会降低烟草薄片的柔软性、口感等,过低的松厚度会影响卷烟的燃烧性能,不利于烟叶充分燃烧,且会加剧CO等有害气体的产生[12-13]。因此,制浆和筛分效果直接关乎纤维浆料抄造成基片或薄片的难易程度及后续成品纸张的质量,进而对再造烟叶的物理性能(松厚度、多孔性、透气性能、燃烧性能等)产生影响。

目前,针对造纸法再造烟叶的工艺参数研究多集中于制浆工艺参数[14-17],而筛分工艺参数的优化研究较少。实际生产往往采用标准筛分工艺参数(如水流速度8 L/min,烟浆固含量0.5%)或仅凭生产经验进行参数粗调,导致再造烟叶中12目以下纤维占比过少或50目以上纤维占比过多,严重影响再造烟叶的松厚度和柔软性。此外,现有方法未考虑工艺参数不确定性对筛分效果的影响。Kriging模型是一种半参数化的插值模型[18],通过对设计空间已知训练样本信息进行线性加权组合,以评估未知测试样本的响应信息[19],最常用的变量-响应隐式关系拟合模型之一,其能够兼顾变量的不确定性。基于此,本文拟以水流速度、烟浆固含量为设计参数,以筛分后烟末颗粒中50目以上纤维质量占比为概率约束,以12目以下纤维质量占比为优化目标,提出基于Kriging模型的造纸法再造烟叶筛分工艺参数优化方法。

1 Kriging模型构建

为降低直接调用筛分实验进行工艺参数设计优化的计算成本,本文采用适应性好、建模简单的Kriging模型。以当前工艺参数为继承点进行继承拉丁超立方采样(ILHS)和筛分实验,在此基础上构建Kriging模型,拟合水流速度、烟浆固含量与12目以下和50目以上纤维质量占比间的隐式关系。

1.1 继承拉丁超立方采样

近似模型的构建依赖于样本点的选择,常用方法有全因子试验设计、部分因子试验设计、正交试验设计[20]、均匀试验设计、拉丁超立方试验设计(LHS)[21]和继承拉丁超立方采样[22]。在再造烟叶筛分工艺参数优化中引入ILHS方法,可以充分利用现有筛分参数下的运行数据,减少优化所需的实验次数,且能够保证Kriging模型在初始优化迭代点附近的近似精度。

ILHS既包含给定继承点,又具有LHS的均匀性[22]。以二维空间4个样本点(包含1个继承点)为例,对ILHS进行描述,如图1所示。首先,将设计空间的两个维度分别等分为4个区间(共16个小网格),移除继承点占据的7个灰色小网格,形成缩减设计空间(如图1b));其次,将缩减设计空间的两个维度分别等分为3个区间(共9个小网格),并用LHS选取3个样本(如图1b)黑色圆点);最后,将图1b)中3个黑色圆点映射到图1a)的空白区域。

图1 ILHS示意图Fig.1 Diagram of inherited Latin hypercube sampling

1.2 样本数据收集

再造烟叶筛分实验流程如图2所示。由图2可知,在给定时间点收集各筛网上的纤维并烘干称重,最后计算各筛网上留存纤维的质量相对于投入试样的质量占比。本文利用鲍尔纤维筛分仪(英特耐森精密仪器有限公司制造)测量烟浆中不同长度纤维的质量占比,并根据不同长度纤维在浆料中的分布情况,优化筛分工艺参数,以提升再造烟叶的填充性能。

本文以当前筛分工艺参数(水流速度8 L/min,烟浆固含量0.5%)为继承点,采用ILHS选取9组水流速度和烟浆固含量数据,并对除继承点外的8组数据开展筛分实验,获得不同筛分工艺参数下的性能响应数据(12目以下纤维质量占比和50目以上纤维质量占比)。ILHS筛分工艺参数及性能响应数据见表1。

1.3 模型构建

不同水流速度和烟浆固含量下的纤维质量占比需要通过筛分实验来确定。而烟浆筛分工艺参数优化涉及多次迭代,每次迭代均需进行筛分实验,优化成本很高。因此,本研究拟利用少量筛分实验数据构建筛分工艺参数与性能响应间隐式关系的Kriging模型,然后在优化迭代中直接调用Kriging模型来获得最优的筛分工艺参数,以大幅降低优化成本。

在Kriging模型[23-25]中,测试样本的响应并不仅仅取决于设计参数,还会受样本点分布的影响。Kriging模型的响应函数(见公式(1))由一个多项式回归模型f(x)Tη(η为多项式系数项)和一个随机过程Z(x)组成[23]。

图2 再造烟叶筛分实验流程Fig.2 Flowchart of sieving experiment for reconstrituted tobacco

表1 ILHS样本点及性能响应数据Table 1 ILHS sample points and performance response data

(1)

2 筛分工艺参数优化

筛分过程中,水流速度和烟浆固含量往往会随着烟浆流动而发生波动,两参数的变化可近似为正态分布。若采用确定性优化设计,则很难真实反应筛分工艺参数对性能响应的影响规律,从而导致优化结果失效。因此,在Kriging模型基础上,使用概率约束和局部自适应采样方法进行烟浆筛分工艺参数优化。具体步骤如下:1)构建烟浆筛分工艺参数优化模型;2)利用局部自适应采样方法(LAS)对Kriging模型进行更新;3)利用蒙特卡罗仿真-序列二次规划(MCS-SQP)计算最优的再造烟叶筛分工艺参数。

2.1 概率约束

以水流速度和烟浆固含量为随机优化参数,12目以下纤维质量占比最大为优化目标,50目以上纤维质量占比为概率约束,构建烟浆筛分工艺参数的可靠性优化模型如下:

s.t:P(g(x)>18)≤Φ(-βt)

5≤d1≤11,0.5≤d2≤1.5

x1～N(d1,0.12)

x2∈N(d2,0.012)

式中:f(x)是目标函数,表示12目以下纤维质量占比;x=[x1,x2]为优化变量,x1和x2分别表示水流速度和烟浆固含量;x=[x1,x2]服从以d=[d1,d2]为均值的正态分布;g(x)为50目以上纤维质量占比,小于18%为企业要求;P(g(x)>18)为50目以上纤维质量占比超过18%的概率;Φ(-βt)为累计概率分布,βt=3为根据企业要求确定的目标可靠度。

2.2 局部自适应采样方法

本文中性能响应与筛分工艺参数之间存在复杂的隐式关系,由表1中ILHS数据构建的Kriging模型精度难以满足优化要求,因此有必要利用序列采样方法对Kriging模型进行更新。在设计优化和可靠性分析过程中,迭代设计点附近的区域相对于其他区域更为重要,且该区域内的极限状态约束边界应被优先考虑[24]。因此,本文引入对迭代设计点区域内约束边界进行重点拟合的LAS选取序列样本点。LAS示意图如图3所示,其中,黑色圆点为初始的ILHS样本点,x为序列样本点,d0为初始设计点,d1～3为第1到3次迭代设计点,dopt为最优设计点,绿色椭圆形为迭代设计点的局部采样区域。由图3可知,在LAS方法中,序列样本点大多位于迭代设计点附近的小区域中,因此能够实现概率优化求解过程中样本利用率的最大化。

图3 LAS示意图Fig.3 Diagram of local adaptive sampling method

2.3 优化流程

基于ILHS和LAS的可靠性优化流程如下:

1)以当前运行的筛分工艺参数为继承点,利用ILHS选取9个样本点作为初始样本集合S0。

2)通过纤维筛分实验获取S0处的12目以下纤维质量占比和50目以上纤维质量占比,并依据现有样本及其响应值建立Kriging模型。

3)在第k次迭代中,依据目标可靠度和迭代点附近概率约束函数的非线性程度计算局部采样区域的半径[26]。

4)在步骤3)确定的局部采样区域内,利用LAS方法选择序列样本点,并通过纤维筛分实验获取12目以下纤维质量占比和50目以上纤维质量占比,然后依据已有样本及其响应更新Kriging模型。

5)利用蒙特卡罗仿真(MCS)[27]计算当前筛分参数下的失效概率及梯度,并利用序列二次规划(SQP)[28]计算下一个筛分参数。

6)如果收敛,则整个筛分工艺参数优化过程结束;否则,k=k+1,转向步骤3),继续后续步骤。

图4 Kriging模型响应面Fig.4 Kriging model response surface

3 结果与分析

利用以当前工艺参数为继承点的ILHS获取初始样本点并构建目标函数及约束函数的初始Kriging模型,进而在概率优化求解过程中利用LAS方法对Kriging模型进行序列更新,最终构建目标函数及约束函数Kriging模型所需的总样本数目为30。本文构建的Kriging模型响应面如图4所示。由图4可知,水流速度和烟浆固含量与12目以下纤维质量占比和50目以上纤维质量占比存在非线性关系。当水流速度和烟浆固含量同步增大时,12目以下纤维质量占比呈下降趋势,而50目以上纤维质量占比呈上升趋势。

基于Kriging模型,利用MCS-SQP计算最优的筛分参数,并分别对优化前后的筛分参数进行纤维筛分实验,最优解处的性能响应对比见表2。由表2可知,优化后的最优水流速度和烟浆固含量分别为6.31 L/min和0.53%,该工艺参数下的12目以下纤维质量占比相较于优化前提升了7.19%;50目以上纤维质量占比相较于优化前降低了4.13%。此外,相较于优化前,优化后的工艺参数能够满足企业的可靠度要求(β≥3)。

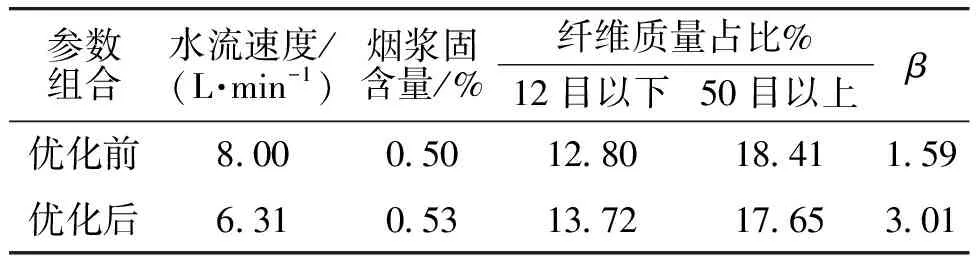
表2 筛分工艺参数优化前后对比Table 2 Comparison of screening process parameters before and after optimization

4 结论

本文以12目以下纤维质量占比为优化目标,以水流速度、烟浆固含量为设计参数,以50目以上纤维质量占比为概率约束,构建了造纸法再造烟叶筛分工艺参数可靠性优化Kriging模型,利用MCS-SQP计算最优筛分工艺参数并对其性能响应进行验证。得到如下结果:采用ILHS开展实验设计,并通过筛分实验获取了9组水流速度和烟浆固含量的12目以下纤维质量占比和50目以上纤维质量占比数据,能够保证Kriging模型在优化迭代点附近的近似精度。利用Kriging模型拟合筛分工艺参数与性能响应间的非线性关系,并采用LAS方法对Kriging模型进行序列更新,取得了良好的建模效果。通过调用Kriging模型及利用MCS-SQP进行优化求解,得到最优的水流速度和烟浆固含量分别为6.31 L/min和0.53%。优化后12目以下纤维质量占比提升了7.19%,50目以上纤维质量占比降低了4.13%,且优化后的工艺参数能够满足企业的可靠度要求(β≥3)。

本文提出的基于Kriging模型的方法能够满足造纸法再造烟叶筛分工艺参数优化需求,未来可将该方法推广于烟草工业其他工艺参数优化中。