多目标遗传算法反演对流层大气温湿廓线研究
2024-03-14李志乾仇志金
李志乾,王 波,胡 桐,仇志金,邹 靖
(齐鲁工业大学山东省科学院海洋仪器仪表研究所,山东 青岛 266061)
0 引言
地基微波辐射计是1种非接触式被动大气遥感器。微波辐射计接收到的特征信号是大气温度、湿度、压力等参数的函数。利用微波辐射计采集到的特征信号,可以反演出不同高度层上的温度、湿度等大气物理参数信息。与常规气象观测相比,微波辐射计可全天候昼夜工作。其时间分辨率高,是现阶段测量大气温度、云液态水和水汽密度剖面的理想探测设备。
微波辐射计反演大气温湿廓线的常用方法有牛顿迭代法[1-2]、统计回归法[3-4]、变分同化法[5]、贝叶斯最大概率估计算法[6]、卡尔曼滤波法[7]、蒙特卡洛法[8]、神经网络法[9-13]等。Solheim等[14]测试了神经网络、牛顿迭代、线性回归和贝叶斯最大概率等反演方法的性能,并与探空数据进行对比,从而分析新算法的反演精度。
近年来,大气微波辐射传输模式模拟精度不断提高。在大气微波方程中,给定1组大气廓线,就能求得唯一解析解,即各通道频率对应的亮温。这就是微波辐射计的正演过程。反演过程是正演的逆运算。逆运算即已知微波辐射计的各通道频率的亮温,反求出观测天顶角方向上的大气廓线。显然,逆过程求解是1个不适定问题。逆运算的求解矩阵是秩亏的,意味着有多组可行解(也称非劣解)。在这种情况下,精确地求得最优解是不现实的,只能得到若干组可行解。因此,需要对可行解设定约束,以从可行解中寻得全局最优解。遗传算法(genetic algorithm,GA) 是模拟生物在自然环境中遗传与进化过程的1种自适应全局优化概率搜索算法,非常适合解决传统方法难以解决的一些非线性或复杂问题。GA在组合优化、机器学习、自适应控制等领域得到广泛应用。
本文提出了1种基于多目标GA的反演对流层大气温湿廓线方法。该方法首先通过构造目标函数,分别使水汽通道和氧气通道的模拟亮温计算值与实测值误差最小;然后,设定合理的温、湿递减率等约束条件,利用GA的快速搜索能力,得到若干组可行解;最后,采用加权平均法寻得全局最优解,即大气温湿廓线。
1 微波辐射计对流层大气廓线反演原理
大气微波传输方程如下[15]。
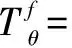
(1)
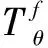
由式(1)可知,大气对微波辐射计观测亮温的贡献来源于2个部分:一部分为宇宙背景辐射经过大气吸收衰减到达辐射计的亮温;另一部分是大气自身辐射经过下层大气衰减后进入微波辐射计的亮温。
大气微波吸收光谱分布如图1所示。
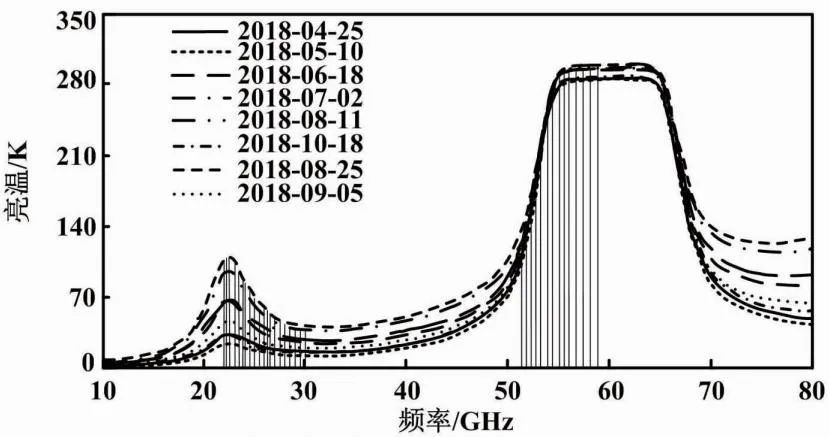
图1 大气微波吸收光谱分布
在图1的10~80 GHz频段,22 GHz附近是水汽吸收带。利用这个频率附近的几个通道可以反演湿度。而在58 GHz附近,氧气吸收较强。本文可以利用这个频率附近的几个通道来反演温度廓线。
以美国Radiometrics公司的MP3000A微波辐射计为例,其共有35个探测通道。通道位置如图1中竖实线所示。其中,水汽通道(N波段)21个,氧气通道(V波段)14个。主设备能获取0~10 km共58层大气参数剖面。
2 大气微波辐射传输模型MonoRTM
MonoRTM模型是美国大气环境研究所(Atmospheric and Environmental Research,AER)开发的、适用于微波波段模拟的大气辐射传输模型。该模型的水汽吸收采用Voigt线型,相关参数来源于HITRAN数据库(如水汽的压力加宽系数、温度加宽系数和自加宽系数等)。水汽吸收谱采用MTCKD模型。该模型考虑到了氧气、氮、二氧化碳和臭氧的压力加宽和自加宽效应。
MonoRTM模型采用FORTRAN语言编写,以源码的形式提供给用户。用户需在Linux环境下自行完成编译。模型以文件为接口,在输入文件中设定各层大气的温度、气压、高度、湿度、液态水含量,以及微波辐射计的通道数、通道波数、观测天顶角等参数信息。通过计算可得到各观测通道的模拟亮温。
(2)
式中:h为大气温、湿、压及液态水的复杂隐函数;g为观测天顶角与波数的隐函数;Θ为耦合算子。
常规探空数据中没有液态水参数,可参照王振会等[16]的方法:当相对湿度小于85%时,云液态水浓度取值为0 g/m3;当相对湿度大于95%时,云液态水浓度取值为2.0 g/m3;当相对湿度在85%~95%之间时,云液态水浓度的取值满足线性关系。本文利用MonoRTM模型计算探空数据温湿压廓线,得到模拟观测亮温。
3 多目标GA反演
GA是由美国的John holland教授于20世纪70年代提出的。它借鉴了达尔文生物进化论和孟德尔遗传定律的基本思想,是1种自适应随机搜索启发式算法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。其在求解较为复杂的组合优化问题时,能够较快地获得较好的优化结果。GA已被广泛应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域,是人工智能的关键技术之一。
在多目标优化问题中,需先构造问题,再选择一定的优化算法,并设置边界条件和约束条件以进行求解。
3.1 经验区间统计学习
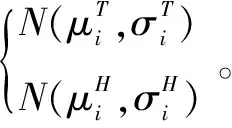
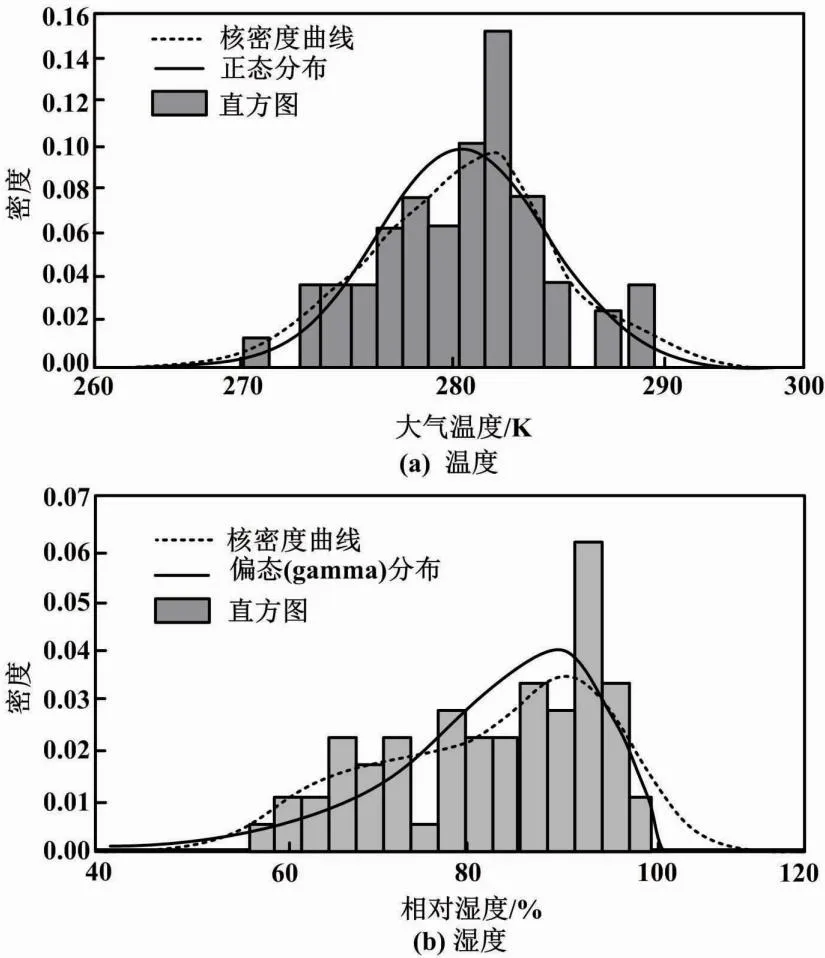
图2 每层的温/湿度分布规律
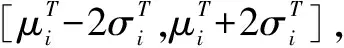
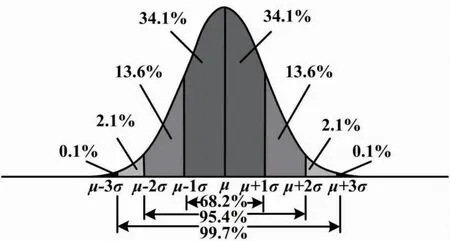
图3 正态分布概率
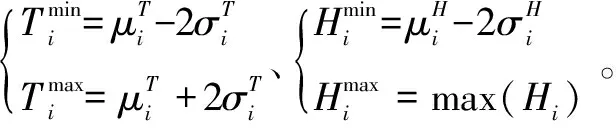
3.2 气压廓线获取
上海探空站气压剖面实测值和模拟计算值比较如图4所示。
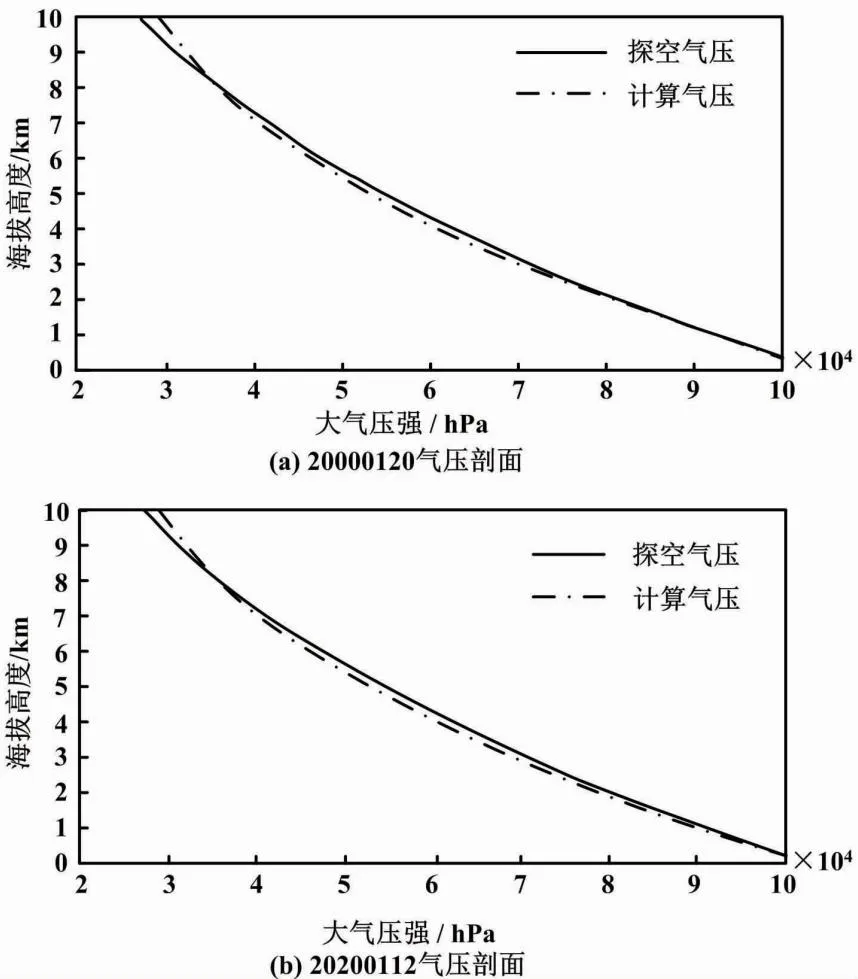
图4 上海探空站气压剖面实测值和模拟计算值比较
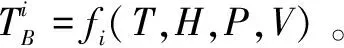
(3)
式中:P0为地面气压,hPa;H为离地海拔,m。
本文根据地面测量气压,利用压-高式计算各高度层上的气压。在智能搜索算法中,实际只有大气温度和相对湿度这2个自变量。这大幅降低了计算复杂度,节省了计算时间。
3.3 多目标函数构建
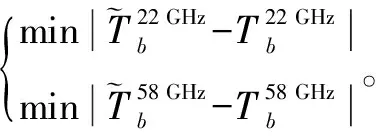
本文在经验区间中随机选取温湿廓线,利用大气微波辐射传输模式MonoRTM计算模拟亮温。衡量2组向量接近程度的方法有曲线曼哈顿距离法、皮尔逊相似度法和向量余弦相似度法等。本文取满足差值向量组(即曲线曼哈顿距离)的最小值的温湿廓线为可行解。微波辐射计观测值与模拟值比较如图5所示。
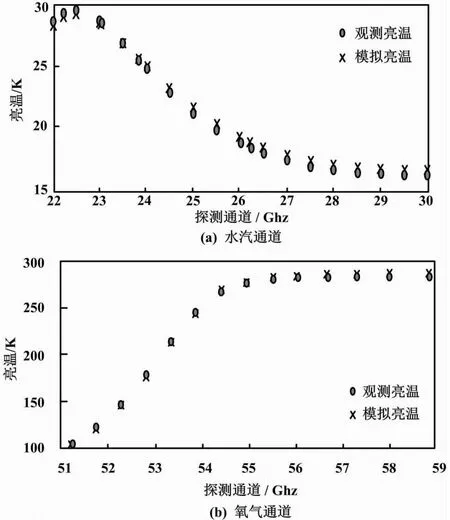
图5 微波辐射计观测值与模拟值比较
在实际计算中,衡量2条曲线相似度的方法有距离均方差法和向量余弦法。
3.4 约束条件
约束条件是抽取多维变量的初步依据,包括等式约束和不等式约束。在多目标GA中,设置一定的合理约束条件,可以从可行解中快速约束出帕累托最优解。但约束条件不宜设置过多,尤其是强约束,否则会导致不可预见的内部自相矛盾。这将引发目标函数振荡,导致无法收敛。
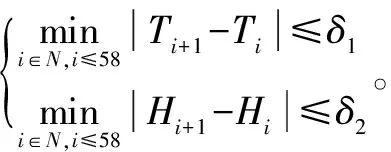
设定约束条件既保留了大气的温湿度垂直递减率,又不会过滤大气温湿度的逆变化。湿度廓线反演结果“锯齿”较多。这与大气中水汽含量的变化非常不稳定有关。对此,可以用卡尔曼滤波或维纳滤波来平滑可行解中的湿度廓线。
3.5 可行解优化处理
多目标GA的结果为多组可行解,通常情况下难以确定哪组可行解为全局最优解。对此,本文设置一定的取舍法则。如:大气温度在短时间内,不会有剧烈波动;与前一时刻温度廓线横向比较,剔除温度变化较大的廓线组。若结果仍多于1组,则以计算加权平均作为全局最优解(满意解)。权重取当前廓线与前一时刻的大气廓线皮尔逊相关系数γ。
(4)
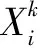
4 仿真比对试验
本文设计了仿真试验,模拟探空站和微波辐射计的同步观测数据,以此验证多目标GA在大气温湿廓线方面的反演能力。本文利用上海站点的探空温湿廓线,采用MonoRTM模型计算大气在MP3000A相关通道上的天顶模拟亮温。本文由模拟亮温结合多目标GA,反推出大气温湿廓线。由于是在经验区间随机取值,反演出的温湿廓线有较多“锯齿”。对此,可利用卡尔曼滤波(或维纳滤波)对反演结果进行平滑处理。试验分别选取201807120800和201808020800这2个探空数据(均判定为阴天)。多目标GA的大气温湿廓线反演结果如图6所示。
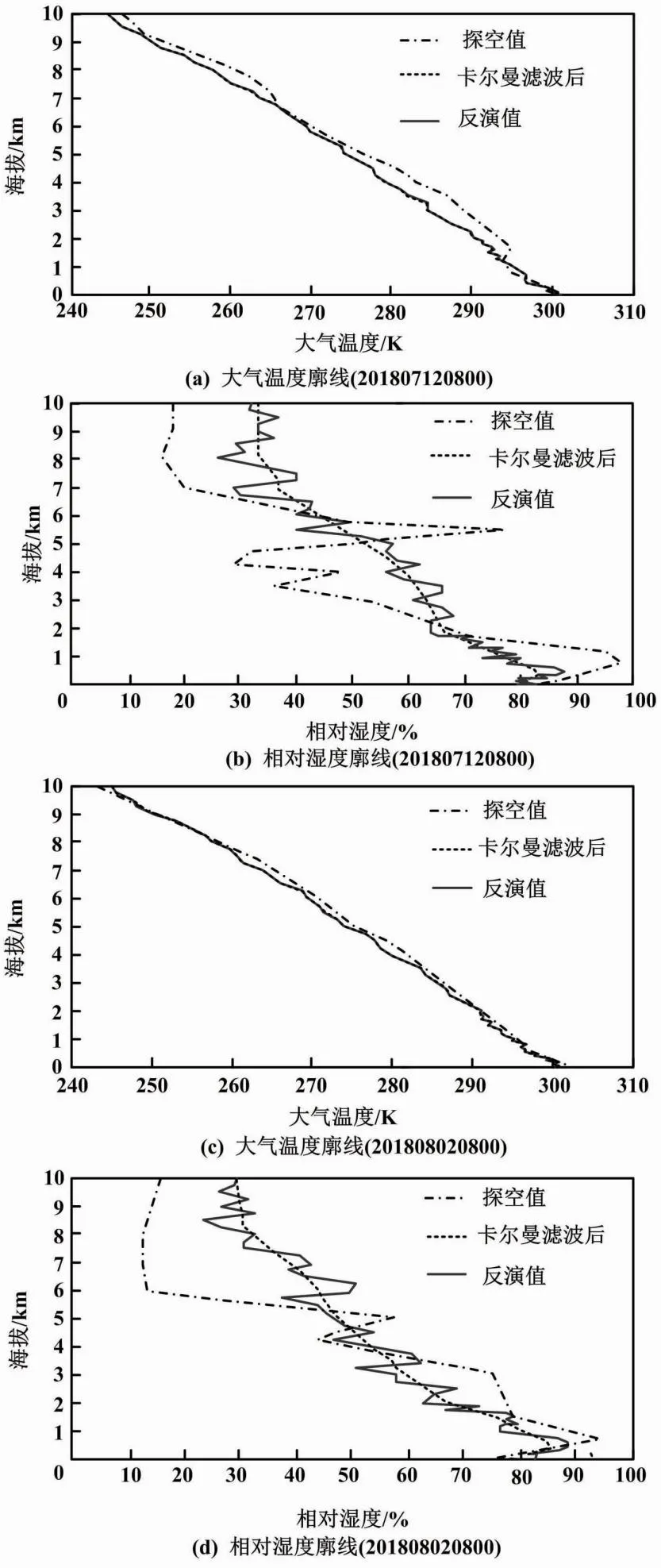
图6 大气温湿廓线反演结果
MP3000A型微波辐射计在下层有更高的路径分辨率。图6中,低层的网格更密。经统计,温度廓线的反演精度为1.5 K,湿度廓线的反演误差为14.2%。
5 反演结果精度验证及误差分析
为进一步验证多目标GA的反演能力和效果,本文以探空资料为标准,计算并比较了各高度层上的反演值平均绝对误差(mean absolute error,MAE)及均方根误差(root mean square error,RMSE)。
(5)
式中:M为MAE值;n取2020年7、8月探空数据(共计62个样本);vi为探空值;ui为反演值,包括大气温湿廓线。
(6)
式中:R为RMSE值。
5.1 大气温度廓线反演结果精度验证
多目标GA大气温度反演廓线误差分布如图7所示。
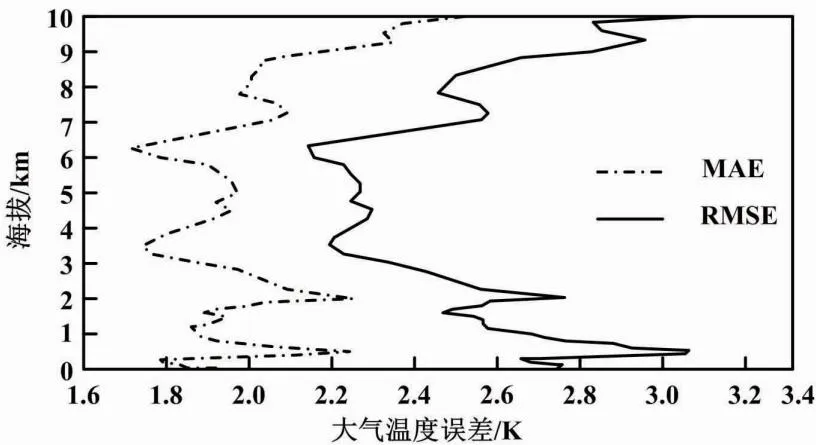
图7 大气温度反演廓线误差分布
与探空仪实测数据相比:在地面500 m,MAE和RMSE均呈线性增大的趋势;在对流层低空3 km以下,MAE在1.8~2.2 K之间、RMSE在3 K以下;在6 km处,MAE接近1.7 K;在6 km以上,RMSE和MAE都呈上升趋势;至10 km处,误差达到最大,MAE在2.5 K左右,RMSE在3.2 K左右。
大气温度廓线反演效果如图8所示。
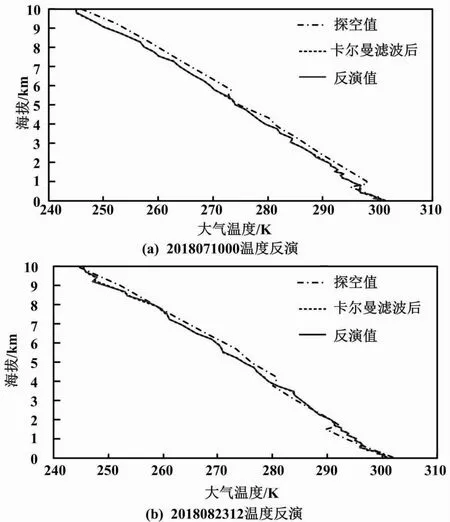
图8 大气温度廓线反演效果
由图8可知,运用多目标GA反演出的温度廓线与探空温度廓线较为接近。这从侧面验证了本文所设计的多目标GA的温度廓线反演能力。反演结果基本可以较好地反映实际的大气温度垂直分布。
5.2 大气湿度廓线反演结果精度验证
多目标GA相对湿度廓线反演误差分布如图9所示。
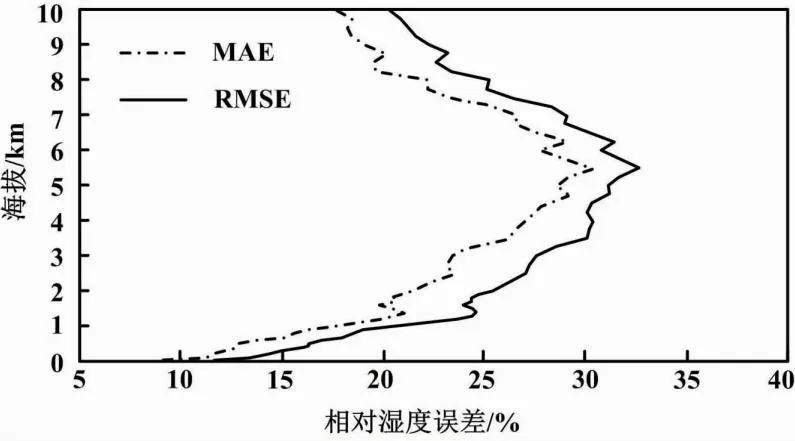
图9 相对湿度廓线反演误差分布
与探空仪实测数据相比:在地面至1 km处,MAE与RMSE都在10~20%以内;在5 km以下,反演误差呈递增趋势,RMSE最大达到32%;在6~10 km,反演误差整体呈递减趋势,下降到20%左右。
相对湿度廓线反演效果如图10所示。
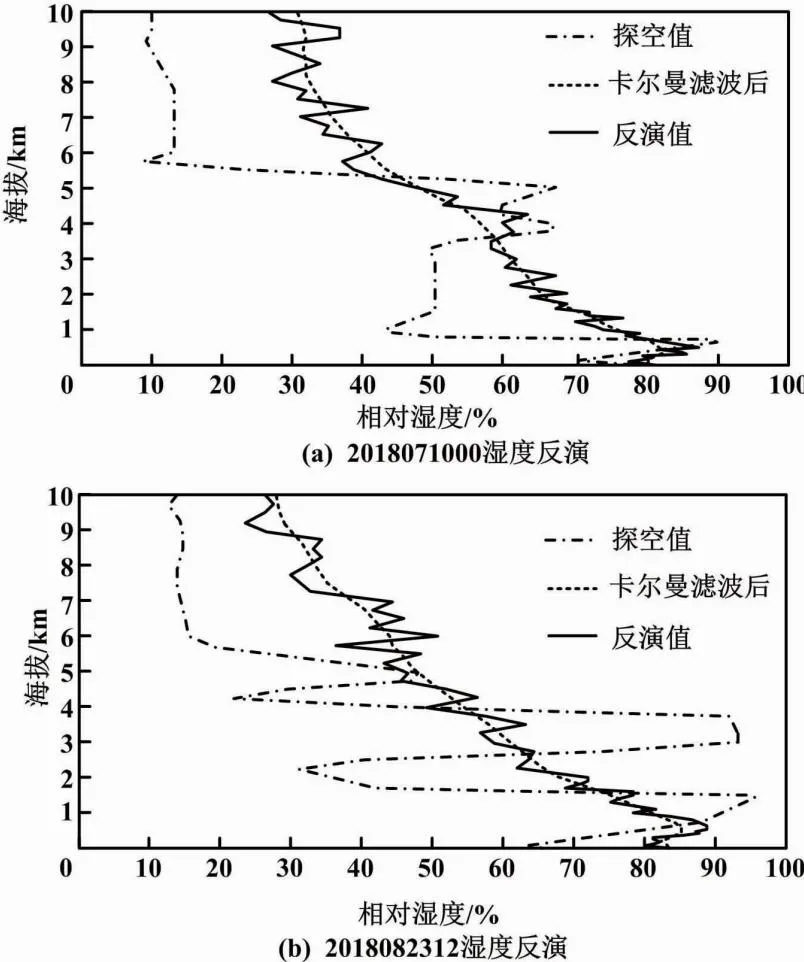
图10 相对湿度廓线反演效果
由图10可知,运用多目标GA反演出的相对湿度廓线基本上与探空相对湿度廓线一致。这很好地刻画了相对湿度的垂直变化规律,从侧面上验证了本文所设计的多目标GA相对湿度廓线的反演能力。
5.3 误差原因分析
本文引进了多目标GA反演模型。相比于微波辐射计自带的神经网络模型,新的反演算法摆脱了对历史数据的完全依赖,并在反演精度上取得了很好的效果。但相比于常规探空观测,该算法还存在一定的误差。造成这一误差的可能原因如下。
①插值计算误差。探空资料层数有限,且温湿廓线的垂直分辨率与气球的上升速度有关,一般为几百米至公里级,而MP3000A型微波辐射计在近地面低空的路径分辨率为50 m。其由低分辨率探空数据插值出高路径分辨率的大气参数剖面数据。因插值数据并非真实数据,必然会引入一定的误差。
②云液水计算误差。云液水含量可由经验式算得。这一近似计算方法本身有一定的误差,应用到MonoRTM大气微波辐射传输模式计算时可能会带来一定的亮温模拟误差,进而影响温湿廓线反演结果。
③探空资料固有误差。探空仪气球上升过程中受风等不稳定气流影响,其探测路径并非地面观测点的垂直路径。用非天顶路径的数据代入反演,也会产生一定的反演误差。
6 算法效率讨论
多目标规划通常存在若干个可行解。多目标优化问题的目标是在可行解中寻找一组具有代表性的帕累托最优解,使总体目标性能尽可能同时达到最优。帕累托最优解的集合称为帕累托前沿。如果决策者没有额外的主观偏好信息,所有帕累托最优解都被认为是同样优秀。多目标优化问题的解如图11所示。
微波辐射计对流层大气廓线反演可看作1个多目标优化问题。由于求解矩阵是秩亏的,解空间中必然有多组可行解。问题的难点在于如何从可行解中得到帕累托最优解,进而寻得理想解(或称满意解)。为此,本文在多目标GA中加入约束条件,如温湿递减(或逆增)率。约束的结果即帕累托前沿。若解集多于1组,可取帕累托前沿的加权平均作为满意解。
基于多目标GA的对流层大气温湿廓线反演,由于求解过程要在经验区间中随机搜索,即边界约束,算法成功率及计算时间受种群大小(种群所含个体数量)、基因交叉率、基因变异率、遗传代数和迭代次数的影响。几种参数组合的计算效率如表1所示。
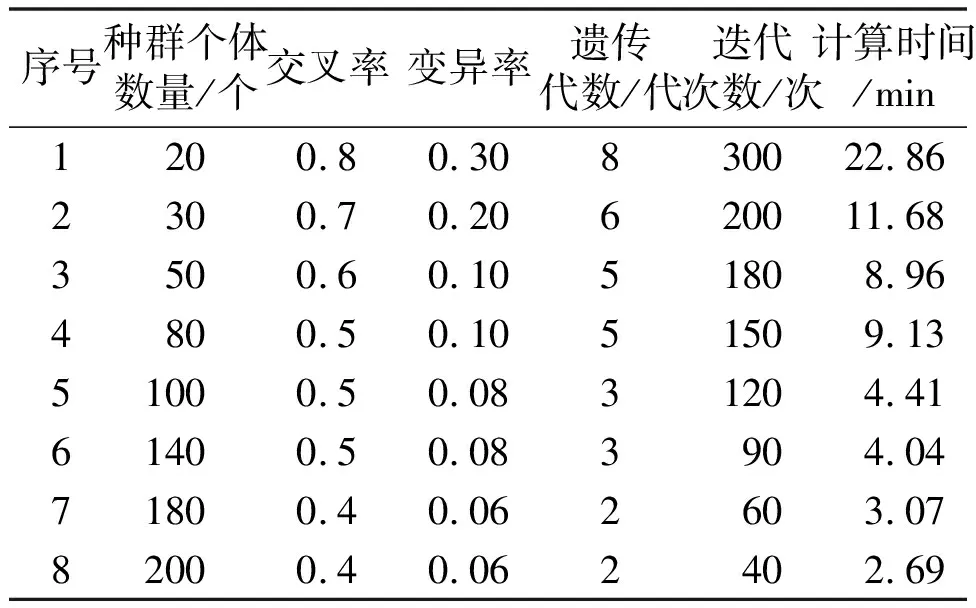
表1 计算效率
由表1可知,合理设置多目标GA参数,可以有效提高计算效率。另外,多核并行计算也可有效缩短计算时间。
7 结论
多目标GA具有优化结果与初始条件无关、算法独立于求解域、鲁棒性较强、适用于求解复杂的优化问题等特点。本文将多目标GA应用于微波辐射计对流层大气温湿廓线反演。GA不需要海量历史数据训练,自适应能力强、应用前景广阔,特别适用于海上或荒漠等历史数据积累匮乏地域。本文使用上海宝山气象站2018~2020年近3年的探空数据,结合MonoRTM大气微波辐射传输模式模拟计算亮温,设计多目标GA,反演了晴空对流层大气温湿廓线,得到以下结论。
①在0~10 km的对流层区域,运用多目标GA反演的温度廓线与探空资料计算的温度廓线有很好的一致性。经RMSE统计,温度廓线反演精度小于或等于1.2 K。
②由于大气中的水汽含量非常不稳定,运用多目标GA反演的湿度廓线,与探空资料计算的湿度廓线相比,总体误差在可接受范围内。RMSE在14%以内。
③由于探空资料里没有云液态水廓线,本文在利用MonoRTM模型计算模拟亮温时加入了云液水改正。反演的云液水廓线依赖于相对湿度廓线,可在云液水精度要求不高的情况下使用。
如何设置更为合理的约束条件,以及利用图形处理器(graphics processing unit,GPU)优化算法提高搜索效率,将是后续研究的重点方向。
