新型气液相变压缩二氧化碳储能系统性能分析

2024-03-14刘仕桢施东波谢永慧

动力工程学报 2024年3期

王鼎, 刘仕桢, 施东波, 谢永慧

(1．国家储能技术产教融合创新平台(中心), 西安 710049;2．西安交通大学能源与动力工程学院, 西安 710049)

随着“双碳”目标逐渐成为全球共识,可再生能源得到大力发展[1]。储能技术作为提高可再生能源普及率的关键技术,能够有效解决可再生能源波动性与间歇性问题,避免可再生能源大规模并网时对电网造成的冲击,有效提高电网安全性与稳定性[2-4]。在现有的储能技术中,压缩空气储能由于容量大、周期长等优点,受到众多学者的关注[5-6]。然而,传统压缩空气储能系统通常需要借助大型地下洞穴储存高压空气,极大地受到地理环境的制约。虽然液化空气储能系统能够避免上述问题,但空气的液化温度极低,对冷源要求极高,系统整体性能较低[7]。

相比于空气,二氧化碳(CO2)的临界点(7.4 MPa、31.4 ℃)更易达到,并且亚临界状态下的CO2能够实现常温下液化。此外,超临界CO2的密度远大于相同压力下的空气,因此能够有效缩小高压工质的储罐容积[8]。基于CO2的以上优点,部分学者提出利用CO2作为储能系统工质。吴毅等[9]提出了一种CO2以液态形式储存的跨临界CO2储能系统,优化后系统的储能效率达到50.4%,储能密度为21.7 kW·h/m3。Zhang等[10]将跨临界CO2储能系统与压缩空气储能系统进行比较,结果表明跨临界CO2储能系统的能量密度是压缩空气储能系统的2.8倍。李玉平等[11]对跨临界CO2储能系统进行了分析,找出了损大的部件及内部原因。

在超临界CO2储能系统方面,He等[12]采用常规及先进分析2种方式对超临界CO2储能系统进行了评估。王永庆等[13]对超临界CO2储能系统进行了热力学与经济性分析。李乐璇等[14]计算分析了超临界CO2储能系统各过程和部件的损,找出了损最大的位置,为超临界CO2储能系统的优化方向提供了参考。

以上研究表明,现有的CO2储能系统主要分为跨临界CO2储能和超临界CO2储能这2种形式。相比于压缩空气储能系统,以上2种CO2储能系统能够有效提升系统的能量密度。但是其整体的压力水平较高,系统最低压力通常在临界压力附近,而系统最高压力则远高于临界压力,这大大增加了系统部件,尤其是高压工质储罐的制造难度与成本,同时对系统的安全性造成威胁。

因此,笔者提出了一种新型气液相变压缩二氧化碳储能系统。该系统利用由弹性材料制成的储气室储存常压气态CO2,而高压CO2则以液态形式储存在储罐中,因此系统整体压力水平低,能够有效降低部件制造难度,提升系统安全性。首先对系统进行了热力学建模,并对典型设计工况下的系统进行了热力学分析、分析与经济性分析;之后研究了CO2冷凝温度、换热器端温差、压缩机以及透平等熵效率对系统储能效率及投资回收周期的影响。

1 系统概述

图1为新型气液相变压缩二氧化碳储能系统的结构,主要部件包括储气室、压缩机、换热器、冷凝器、液态CO2储罐、蒸发器、透平、冷却器、冷水罐、热水罐、冷盐罐、热盐罐。图2为该系统的T-s图,其中:T为温度,K;s为熵,kJ/(kg·K)。整个储能系统分为储能与释能2个阶段。储能时,储气室中的常温常压CO2被压缩机压缩至高温高压状态(1-2),之后分别经换热器1和换热器2放热降温(2-4),将压缩热传递给来自冷盐罐的熔融盐及来自冷水罐的储热水(21-22,11-12),降温后的CO2进入冷凝器由冷却水冷凝为液态(4-5)并储存在液态CO2储罐中,在换热器中吸热升温的熔融盐和储热水分别存储在热盐罐和热水罐中。释能时,液态CO2首先在蒸发器中被来自热水罐的部分储热水蒸发为气态(5-6),之后进入换热器3与来自热水罐的剩余储热水进一步换热升温(6-7)。中温高压的CO2进入换热器4,进一步与来自热盐罐的熔融盐换热升温后,进入透平膨胀做功(7-9)。最后,膨胀至常压的CO2储存在储气室中,在换热器3与蒸发器中放热降温的储热水分别经冷却器1与冷却器2冷却后回到冷水罐存储,在换热器4中放热降温后的熔融盐存储在冷盐罐中。

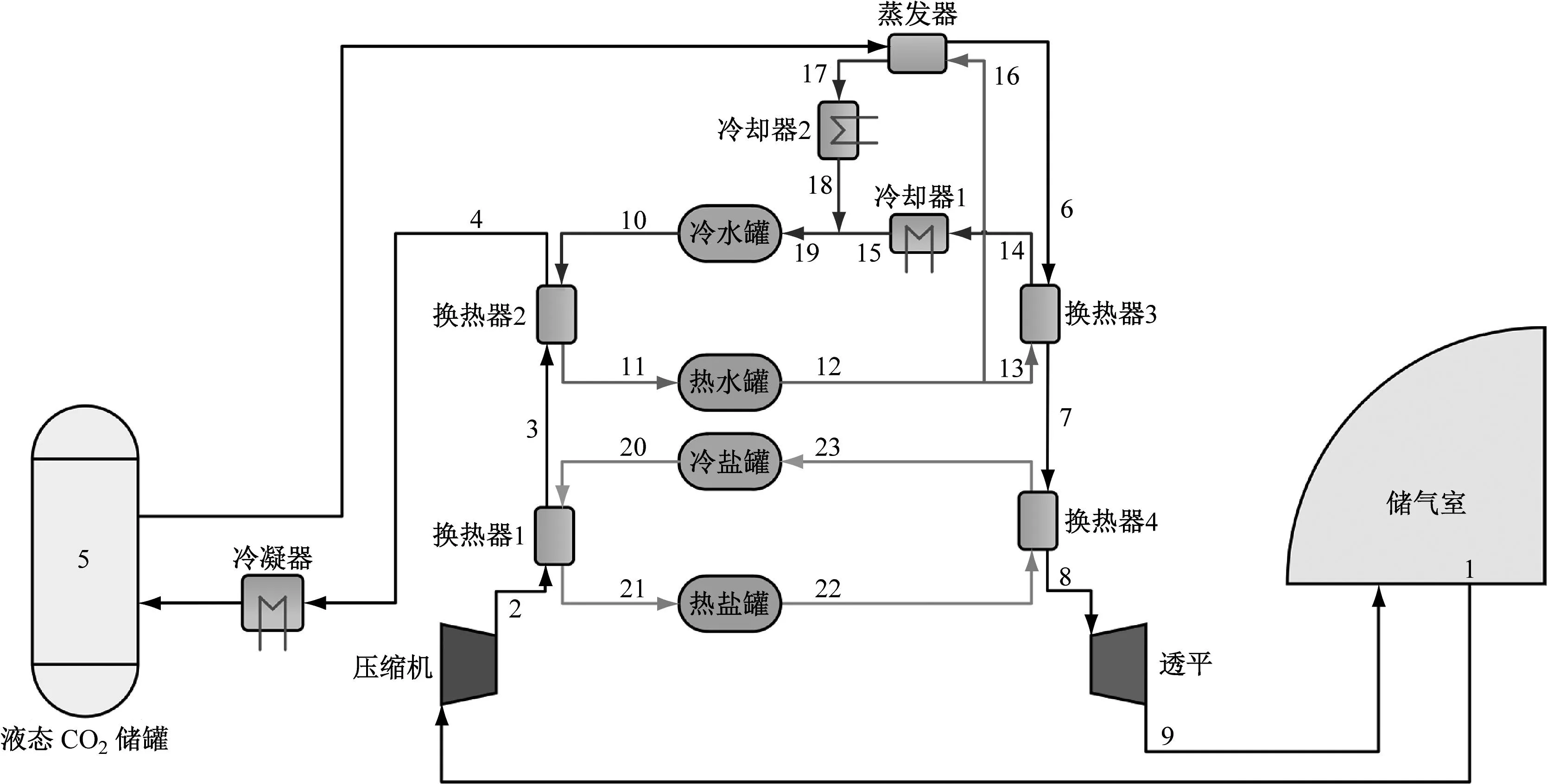
图1 气液相变压缩二氧化碳储能系统结构示意图

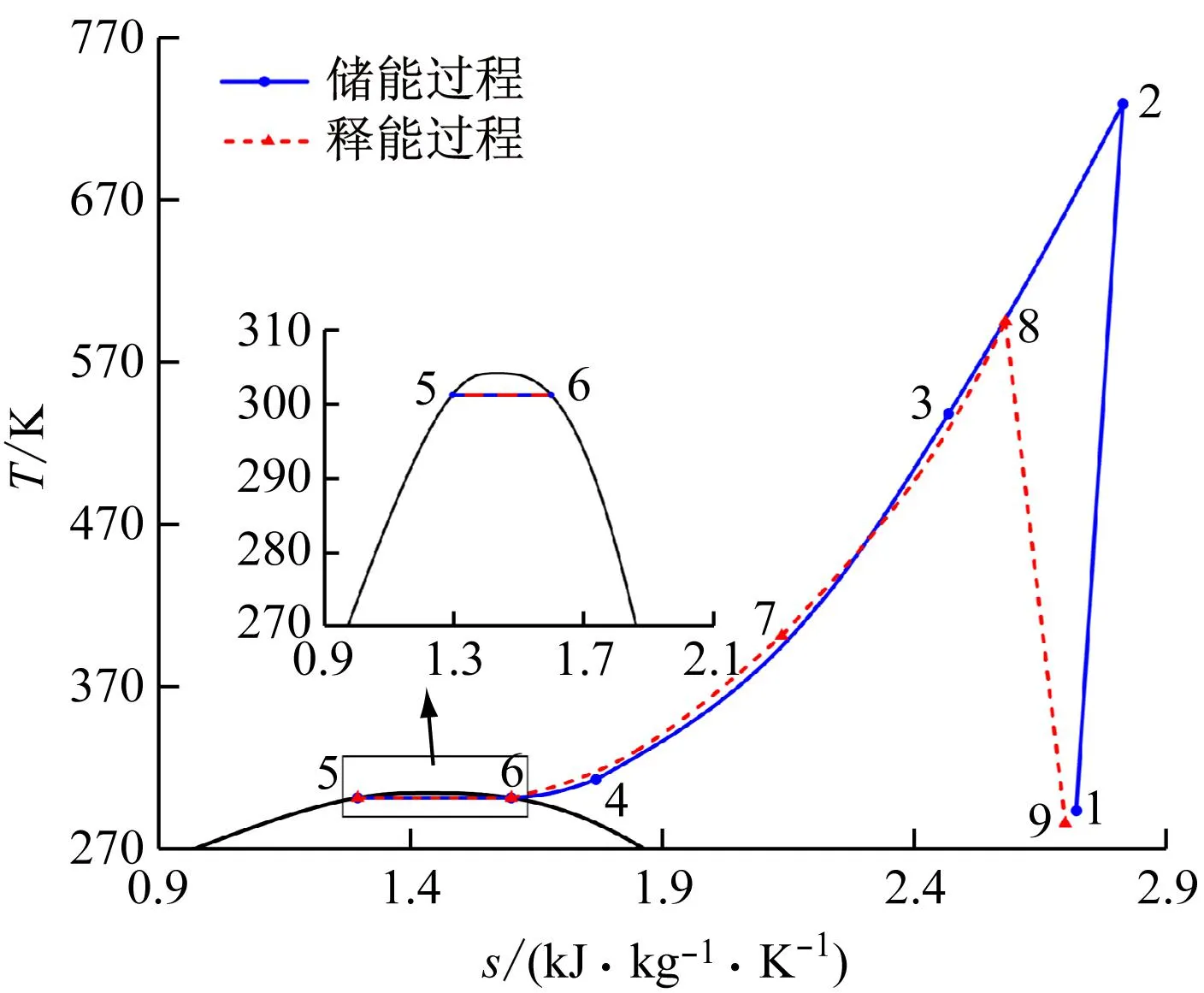
图2 新型气液相变压缩二氧化碳储能系统T-s图

2 系统假设及数学模型

为了简化数学模型,本文进行如下假设[15-17]:

(1) 系统运行在稳定工况下,忽略动能及势能变化的影响。

(2) 忽略管道和管道的压力损失与热量损失。

(3) 冷凝器与蒸发器最小换热温差为3 K,其余换热器最小换热温差为5 K。

(4) 冷却水进口状态为常温常压,且水量充足,冷凝及冷却过程中水温恒定。

(5) 系统储能阶段与释能阶段的运行时长相同,2个阶段的CO2质量流量也相同。

基于以上假设,结合热力学第一定律及热力学第二定律,对系统进行热力学建模。

储能过程压缩机耗功率PC、压缩机等熵效率ηC,释能过程透平输出功率PT、透平等熵效率ηT分别定义为

PC=qm,CO2(hout-hin)

(1)

(2)

PT=qm,CO2(hin-hout)

(3)

(4)

式中:qm,CO2为CO2质量流量,kg/s;hout为部件出口焓,kJ/kg;hin为部件出口焓,kJ/kg;hout,s为等熵过程部件出口焓,kJ/kg。

由于系统存在熔融盐和水2种储热介质,因此换热器换热量的计算方式也分为2种,定义CO2-熔融盐换热器换热量QHE,salt为

QHE,salt=qm,CO2ΔhCO2=qm,saltcsaltΔTsalt

(5)

式中:ΔhCO2为换热器进、出口CO2的焓差,kJ/kg;qm,salt为熔融盐的质量流量,kg/s;csalt为熔融盐比热容,kJ/(kg·K);ΔTsalt为换热器进、出口熔融盐温差,K。

定义CO2-水换热器换热量QHE,water为

QHE,water=qm,CO2ΔhCO2=qm,waterΔhwater

(6)

式中:qm,water为水的质量流量,kg/s;Δhwater为换热器进、出口水的焓差,kJ/kg。

由于本文系统中的换热器均采用逆流式换热器,因此换热器的热端温差ΔTHE,hot与冷端温差ΔTHE,cold计算方式相同,可以表示为

ΔTHE,hot=Th,in-Tc,out

(7)

ΔTHE,cold=Th,out-Tc,in

(8)

式中:Th,in为部件热流体侧进口温度,K;Tc,out为部件冷流体侧出口温度,K;Th,out为部件热流体侧出口温度,K;Tc,in为部件冷流体侧进口温度,K。

储能系统的储能效率ηstor可定义为释能过程总输出功与储能过程总耗功的比值,即

(9)

式中:tr为释能过程工作时长,s;ts为储能过程工作时长,s;

储能系统的能量密度DES可定义为系统总输出功与系统存储容器总容积的比值,即

(10)

式中:Vi为存储容器i的容积,m3。

除熔融盐外,系统其余状态点j处工质的Ej可定义为

Ej=qm,j[(hj-h0)-T0(sj-s0)]

(11)

式中:qm,j为状态点j处工质的质量流量,kg/s;hj为状态点j处工质的焓,kJ/kg;h0为环境条件下工质的焓,kJ/kg;T0为环境温度,K;sj为状态点j处工质的熵,kJ/(kg·K);s0为环境条件下工质的熵,kJ/(kg·K);

(12)

式中:Tout为部件出口熔融盐温度,K;Tin为部件进口熔融盐温度,K。

ED,k=EF,k-EP,k

(13)

式中:EF,k为部件k的燃料,kW;EP,k为部件k的产品,kW。

定义部件k的效率εk为部件产品EP,k与燃料EF,k的比值[18],即

(14)

系统各主要部件的成本计算方式如表1[13]所示。应当指出,主要部件的成本只是储能系统总成本的一部分,但是在系统设计过程中可以认为其余部分的成本与主要部件的成本成一定比例,因此本文用主要部件成本来表征储能系统的成本。

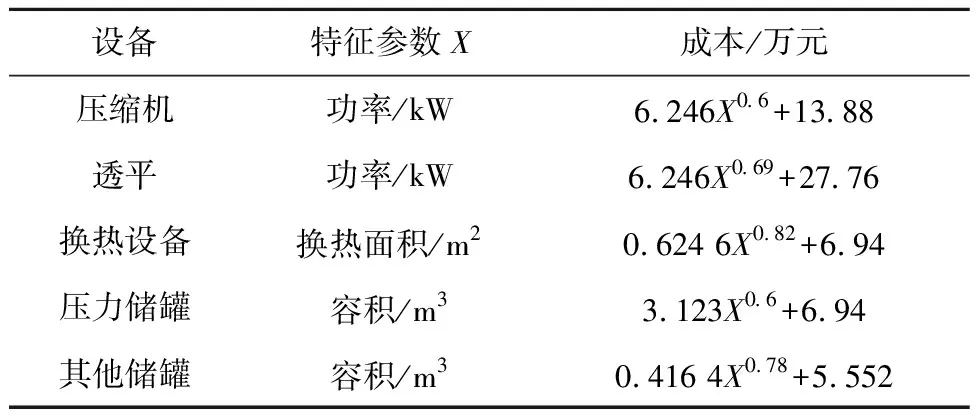
表1 储能系统主要部件成本计算方式

此外,本文采用总传热系数的近似值对换热面积进行估算,对于各换热器取3.0 kW/(m2·K),对于冷凝器及冷却器取2.0 kW/(m2·K),对于蒸发器取1.6 kW/(m2·K)[19]。此外,系统中的储气库可视为半球体,其成本可按投影面积1 000元/m2进行估算。

系统的投资回收周期Y可表示为系统总成本Zsystem与年收益Eyear的比值[13],即

(15)

Eyear=N(C2PTtr-C1PCts)

(16)

式中:N为系统年运行天数;C2为高峰电价,元/(kW·h);C1为低谷电价,元/(kW·h)。

3 结果与分析

3.1 典型设计工况分析结果

利用MATLAB软件建立储能系统仿真程序,利用物性数据库查取系统中的CO2和水的热力学性质,熔融盐则选择应用较为广泛的Solar Salt(质量分数为60%的NaNO3+质量分数为40%的KNO3),其物性可由文献[20]获取。系统典型设计工况的参数设置如表2[13,21-22]所示。

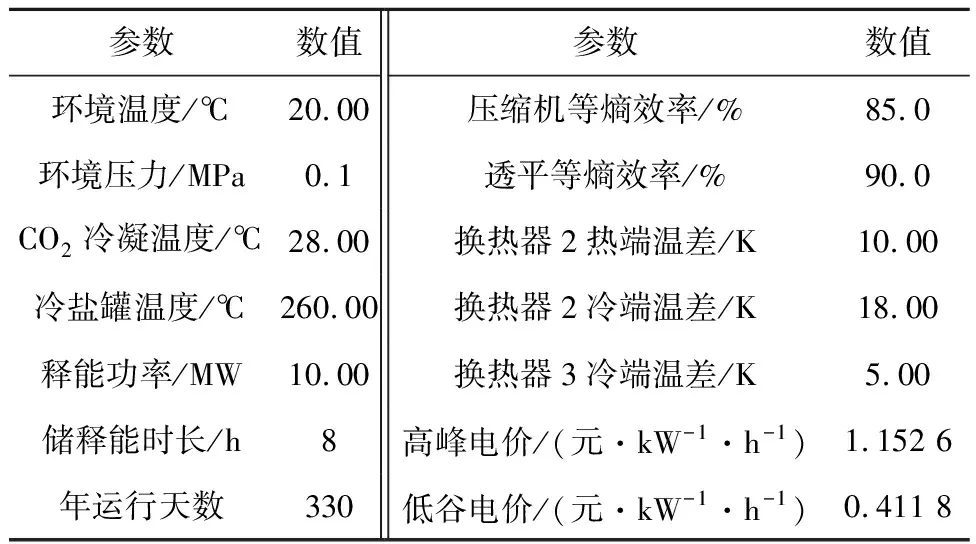
表2 储能系统典型设计工况参数设置

在表2给出的典型设计工况参数下,储能系统各状态点热力学参数计算结果如表3所示。系统主要性能参数的计算结果如表4所示。由表4可知,典型设计工况下系统储能效率达到65.35%。而由于采用气态存储低压CO2,因此系统储能能量密度为0.144 kW·h/m3。

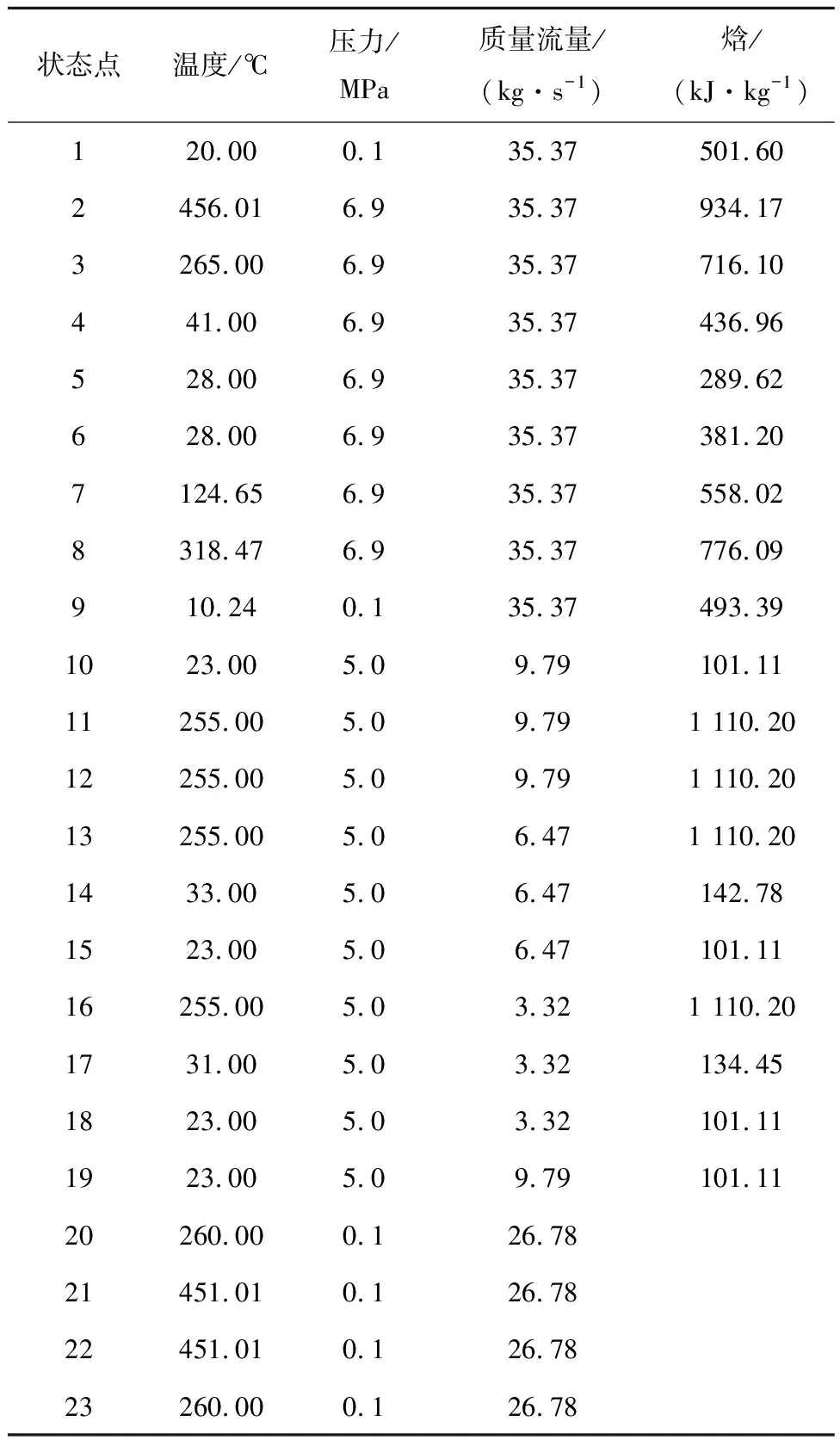
表3 系统各状态点热力参数计算结果

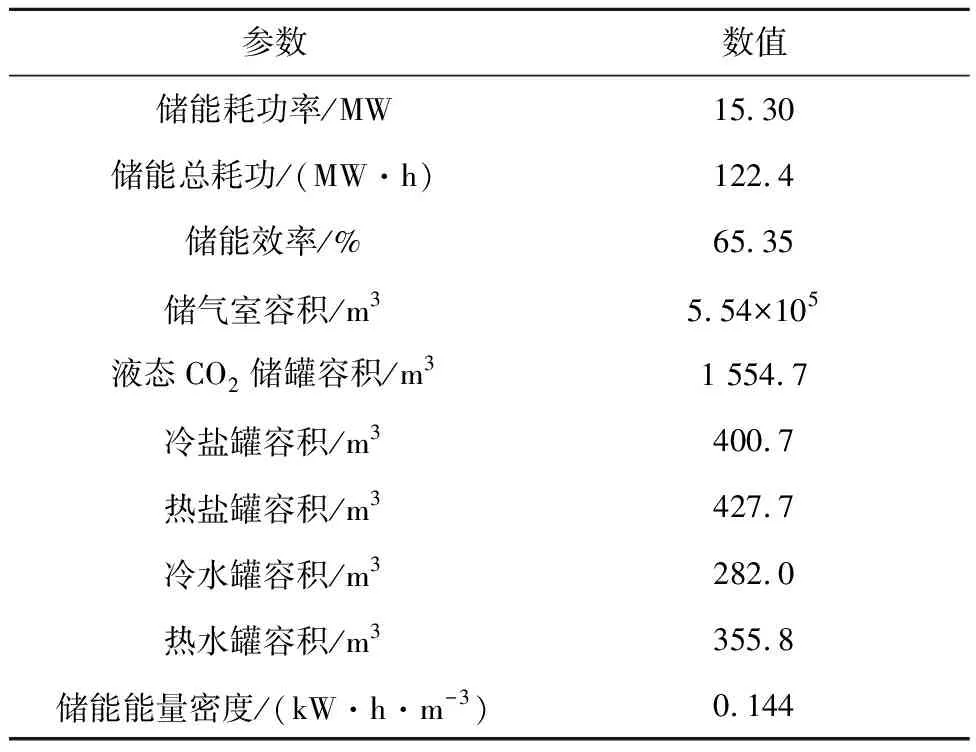
表4 系统主要性能参数计算结果

表5 储能系统各部件分析结果

Tab.5 Exergy analysis results of each component in the energy storage system

部件燃料/MW产品/MW损/MW效率/%压缩机15.3014.340.9693.73换热器14.124.090.0399.19换热器22.752.700.0598.16冷凝器7.467.300.1697.75蒸发器0.910.090.829.41换热器31.780.781.0043.75换热器44.093.081.0175.28透平11.2310.001.2389.01冷却器10.660.661.10×10-399.83冷却器21.291.293.00×10-399.77

图3 储能系统各部件损及效率

储能系统各部件成本的计算结果如表6所示。将表6中各部件的成本相加可知,典型设计工况下储能系统的总成本约为7 587.2万元。而由式(16)以及表2中的电价可知,系统年收益约为1 379.4万元,由式(15)可知系统投资回收周期约为5.50 a。

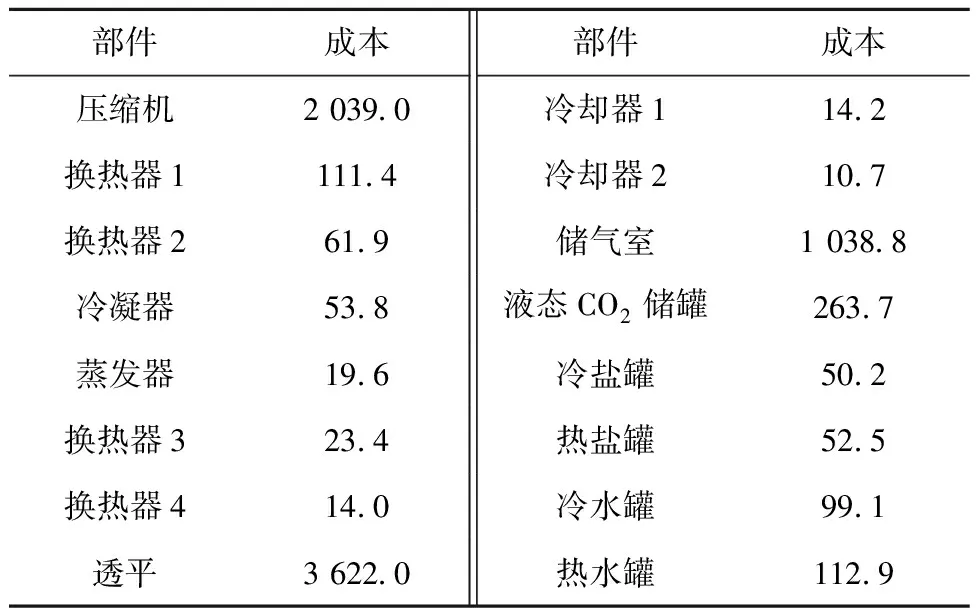
表6 储能系统主要部件成本计算结果

3.2 敏感性分析

本节选取CO2冷凝温度、换热器2热端温差及冷端温差、换热器3冷端温差、透平等熵效率和压缩机等熵效率这5个参数作为系统的决策变量,计算分析其变化对系统储能效率及系统投资回收周期的影响。决策变量的变化范围如表7[23-24]所示。

表7 储能系统决策变量的变化范围

图4为不同CO2冷凝温度(T5)下系统储能效率及投资回收周期随换热器2热端温差的变化情况。可以看出,随着换热器2热端温差的增大,系统储能效率逐渐下降,投资回收周期逐渐上升,且换热器2热端温差对两者的影响并不明显。以CO2冷凝温度28 ℃为例,当换热器2热端温差由10 K增大至30 K时,系统储能效率从65.35%降低至65.22%,仅下降了0.13百分点;投资回收周期则从5.50 a上升至5.51 a,仅上升了0.01 a。一方面,储能阶段换热器2热端温差增大,将导致换热器2出口处储热水温度降低,并最终使透平进口CO2温度降低,单位质量工质的做功能力下降。为了保持恒定的输出功率,CO2质量流量将上升,使储能过程压缩机耗功率上升;另一方面,由于换热器2热端温差不影响换热器进、出口CO2的参数,因此单位质量CO2在换热器2中的放热量不变,而CO2质量流量的上升将增加储能过程回收的热量,即释能过程可利用的热量有所增加,这对于储能效率是有利的。在上述两方面的共同作用下,储能效率呈缓慢下降趋势。而系统储能效率的下降将导致系统收益降低,从而延长系统的投资回收周期。

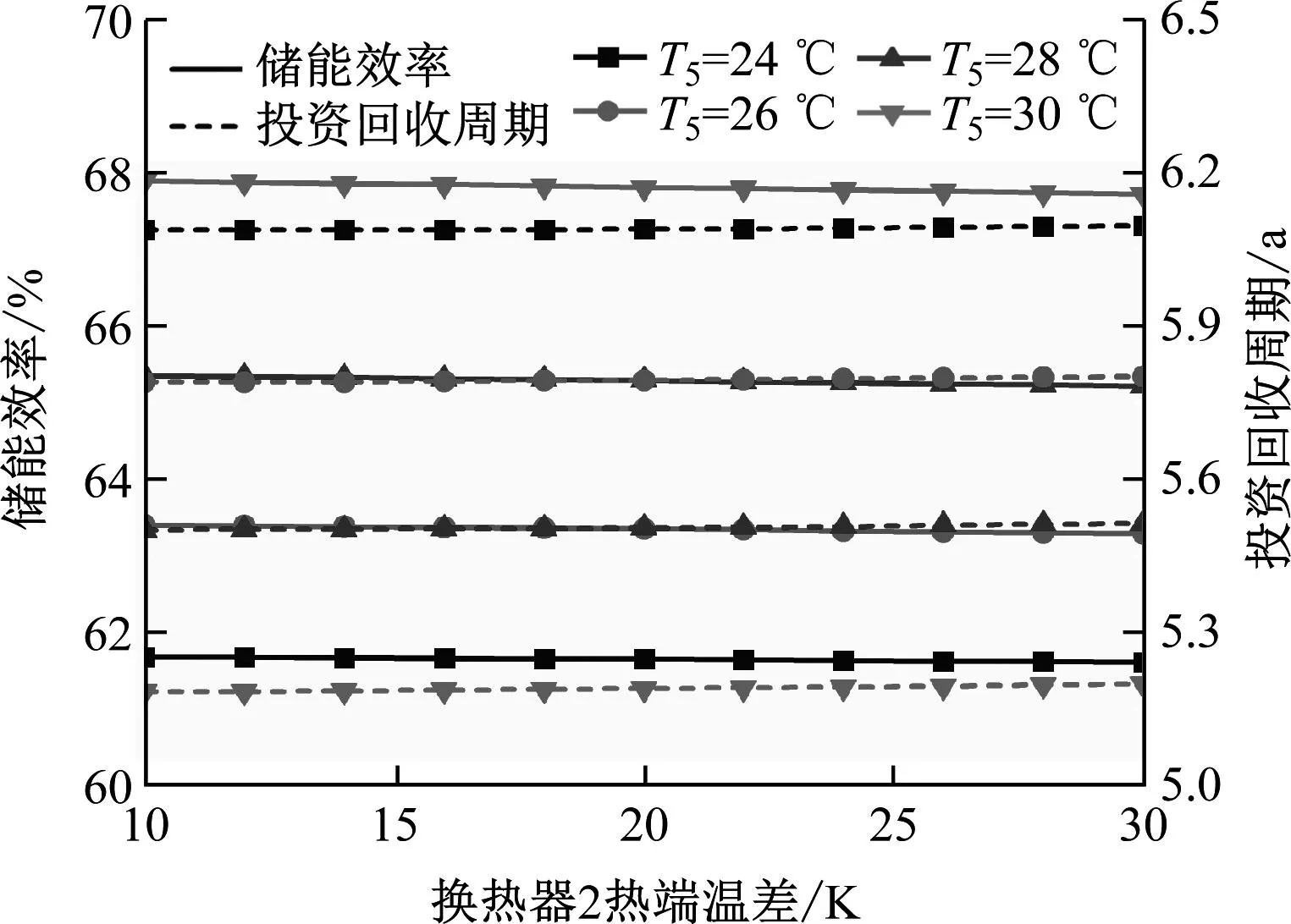
图4 不同CO2冷凝温度下换热器2热端温差对储能效率和投资

不同CO2冷凝温度下换热器2冷端温差对系统储能效率及投资回收周期的影响如图5所示。随着换热器2冷端温差的增大,系统储能效率同样呈下降趋势,投资回收周期也同样逐渐延长,且换热器2冷端温差对两者的影响更为明显。以CO2冷凝温度28 ℃为例,当换热器2冷端温差由16 K增大至30 K时,系统储能效率从65.93%下降至62.51%,下降约3.42百分点;投资回收周期则从5.43 a上升至5.89 a。这是由于换热器2冷端温差的增大将导致单位质量CO2在换热器2中的放热量减小,即释能过程可利用的热量有所降低,进而使得单位质量CO2做功能力下降,因此系统储能效率逐渐下降,系统收益降低,投资回收周期延长。此外,由于CO2在临界点附近比热变化较大,换热过程中最小换热温差通常出现在换热器内部。因此,换热器2冷端温差不能过低,以避免换热器产生“夹点”问题。同时,随着CO2冷凝温度的提升,所允许的最小换热器2冷端温差逐渐增大。这是由于CO2冷凝温度提升使换热器2出口CO2更接近临界点,比热变化更加剧烈,需要提高冷端温差才能满足“夹点”约束。

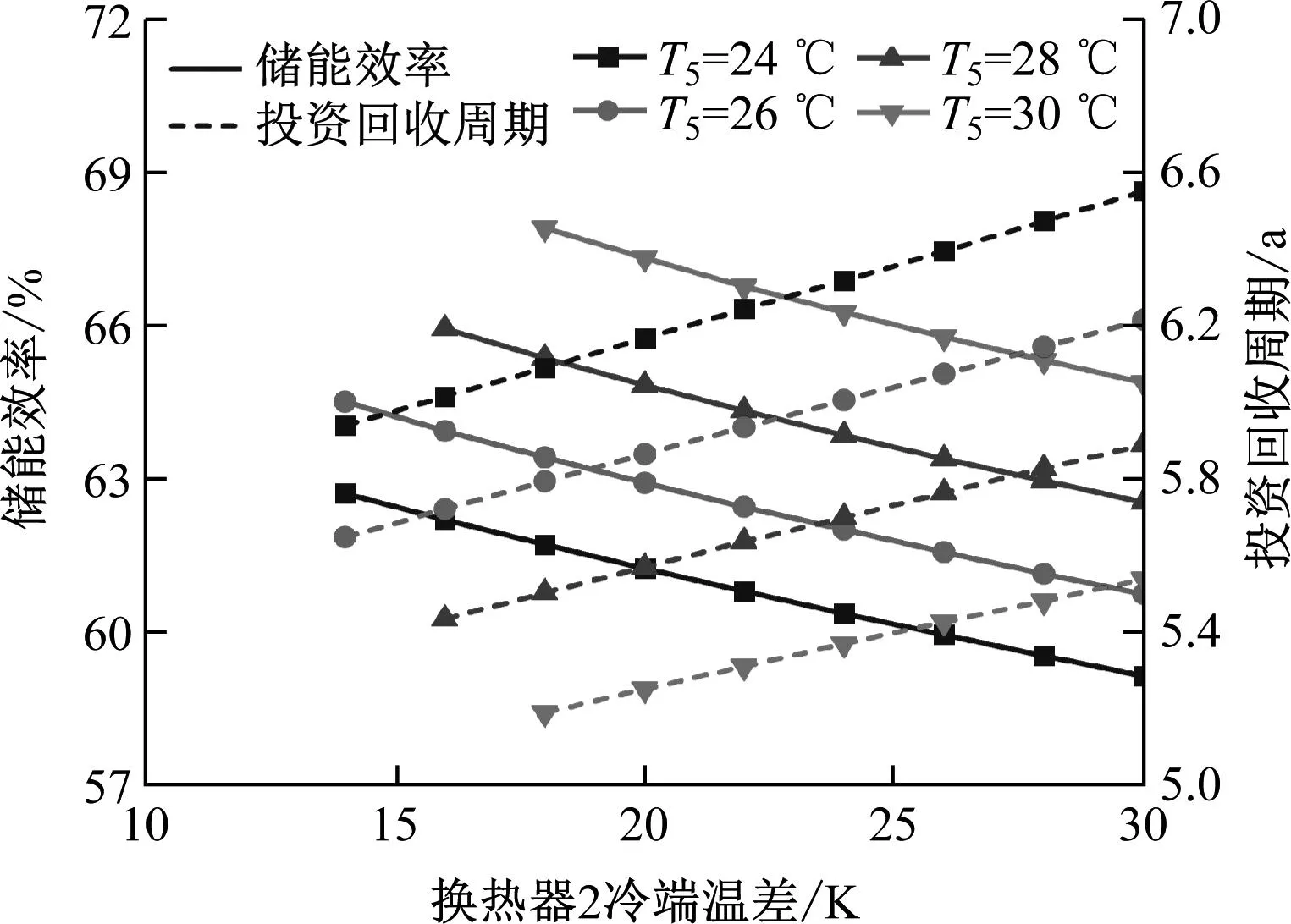
图5 不同CO2冷凝温度下换热器2冷端温差对储能效率和投资回收周期的影响

图6为不同CO2冷凝温度下换热器3冷端温差对系统储能效率及投资回收周期的影响。系统储能效率随着换热器3冷端换热温差的增大逐渐降低,投资回收周期的变化与之相反。以CO2冷凝温度28 ℃为例,当换热器3冷端温差从5 K增大至25 K时,系统储能效率从65.35%下降至63.49%,投资回收周期从5.50 a上升至5.76 a。这是由于换热器3冷端温差的提升降低了单位质量储热水在换热器3中的放热量,即释能过程可利用的热量有所降低,单位质量CO2的做功能力下降,最终使系统热力学性能与经济性能均有所下降。

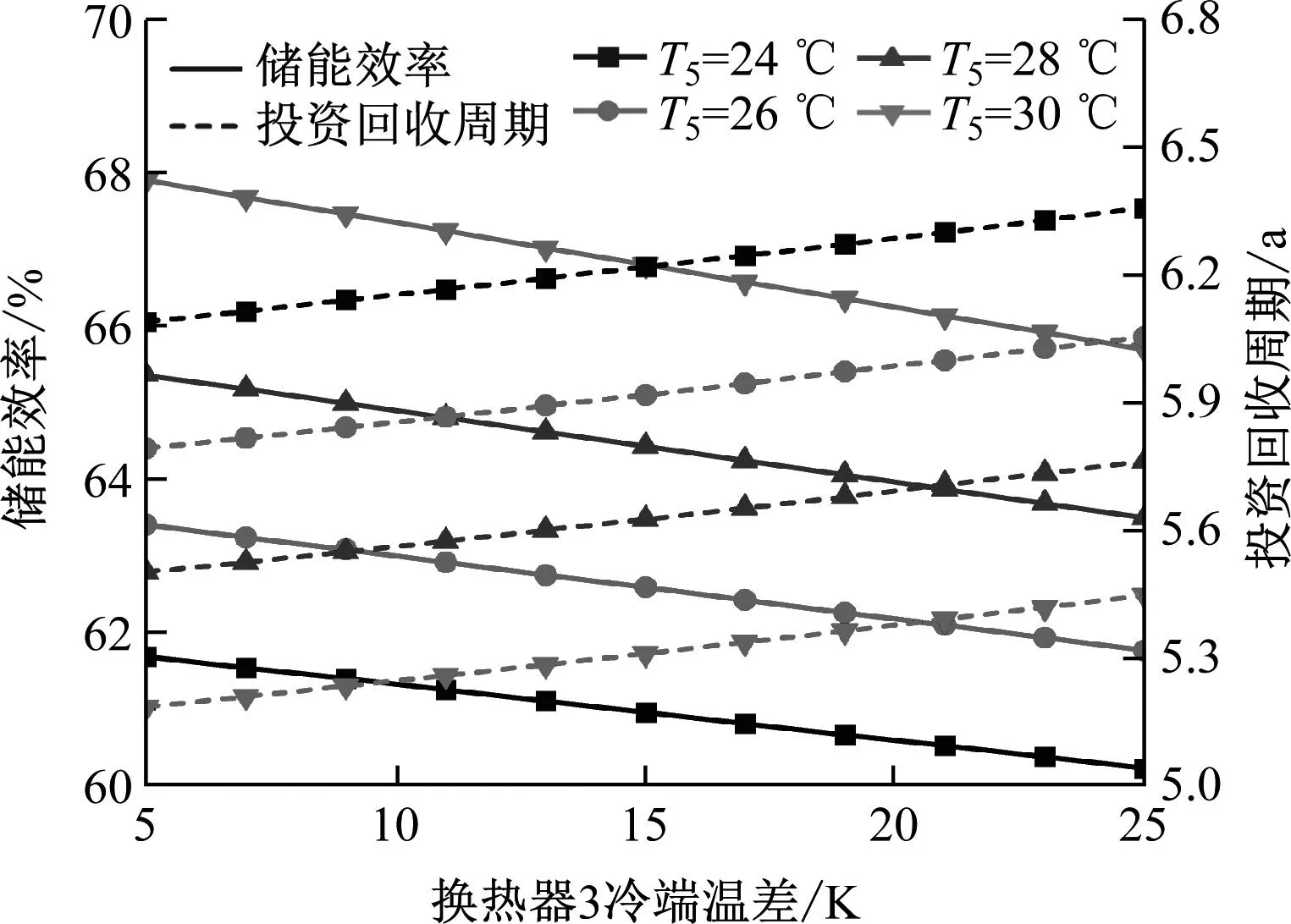
图6 不同CO2冷凝温度下换热器3冷端温差对储能效率和投资回收周期的影响

图7为不同CO2冷凝温度下系统储能效率及投资回收周期随压缩机等熵效率的变化情况。可以看出,随着压缩机等熵效率的增大,系统储能效率逐渐增大,而投资回收周期逐渐缩短。以CO2冷凝温度28 ℃为例,当压缩机等熵效率从80.0%增长至90.0%时,储能效率由64.59%增长至66.08%,而投资回收周期则由5.54 a下降至5.46 a。一方面,压缩机等熵效率的增大意味着压缩机性能的改善,相同条件下压缩单位质量CO2的耗功量大大降低;另一方面,压缩机等熵效率的增大还会导致压缩机出口CO2温度下降,透平进口CO2温度下降,单位质量CO2做功能力有所下降。而在这两种效应的共同作用下,储能过程压缩机耗功率呈下降趋势,系统收益有所增长。因此,随着压缩机等熵效率的增大,系统储能效率有所提高,而投资回收周期逐渐缩短。

图7 不同CO2冷凝温度下压缩机等熵效率对储能效率和投资回收周期的影响

不同CO2冷凝温度下透平等熵效率对系统储能效率及投资回收周期的影响如图8所示。增大透平等熵效率能有效提升系统储能效率并缩短投资回收周期。以CO2冷凝温度28 ℃为例,当透平等熵效率从82.0%提升至92.0%时,系统储能效率由59.54%提升至66.81%,提升约7.27百分点;投资回收周期由6.46 a下降至5.32 a,下降约1.14 a。产生这种结果的原因为:透平等熵效率的提升意味着透平性能的改善,相同条件下单位质量CO2在其膨胀过程中所能输出的功增加,有利于系统储能效率的提升,大大改善了系统的热力学性能与经济性能。因此,系统储能效率呈不断增大的趋势,且投资回收周期不断缩短。

图8 不同CO2冷凝温度下透平等熵效率对储能效率和投资回收周期的影响

此外,由以上分析还可以看出,随着CO2冷凝温度的提升,系统储能效率呈增大趋势,而投资回收周期的变化与之相反。其他决策变量保持不变,当CO2冷凝温度从24 ℃提升至28 ℃时,储能效率由61.68%增长至67.89%,投资回收周期由6.09 a下降至5.18 a。在储能阶段,随着CO2冷凝温度的提升,压缩机压比逐渐增大,在储能过程总耗功量增加的同时,压缩机出口CO2温度也会随之提升,即储能过程能够回收更多热量用于释能。在释能阶段,CO2冷凝温度的提升一方面增大了透平膨胀比,提升了释能过程的输出功量;另一方面降低了CO2的相变潜热,使更多的储热水能够进入换热器3用于加热CO2,单位质量CO2的做功能力提升。在以上因素综合作用下,系统储能效率逐渐增大,投资回收周期随之缩短。

综合参数分析的结果可知,降低换热器2冷端、热端温差或换热器3冷端温差,增大CO2冷凝温度或提升压缩机、透平等熵效率均能够有效改善系统的热力学性能和经济性能。但是考虑到“夹点”问题对换热器2的影响,换热器2的冷端温差不能过低。