含多类型储能的综合能源系统低碳经济运行双层优化方法研究
2024-03-14李金航潘佩媛刘文毅
李金航, 佟 曦, 陈 衡, 潘佩媛, 徐 钢, 刘文毅
(华北电力大学 能源动力与机械工程学院, 北京 102206)
随着全球能源结构向低碳形态快速转变,构建低碳清洁的能源体系迫在眉睫[1]。作为我国的主要碳排放源,能源行业的绿色低碳转型将成为推动“双碳”目标早日实现的重要举措[2]。面对可再生能源的波动性与间歇性,通过构建多类型储能系统-综合能源系统(MTES-IES)实现异质能源子系统的协调互补与最优运行,将是实现可再生能源充分消纳的有效方式[3-5]。因此,需要对多类型储能在综合能源系统的优化配置调度进行研究。
学者们针对综合能源系统优化调度与规划进行了广泛研究。杜传铭等[6]建立了光-气互补冷热电联产系统,该系统采用阶梯式释能,运用遗传算法优化之后,提高了系统总体的经济性。王智等[7]针对冷热电联产系统的运行经济性,提出了基于日前-日内多时间尺度滚动优化模型。朱海南等[5]在IES规划时,构建了一种综合考虑系统经济性和碳排放的电-气IES多目标随机优化规划模型,利用混合整数二次约束规划,最终实现了系统整体最优规划。秦婷等[8]将碳交易机制引入调度模型,提出了电-气-热IES分层低碳调度方法,验证了电-气-热多能协调运行模式和碳交易机制对IES调度决策经济性和低碳性的促进作用。王守文等[9]构建了一种含改进生物质燃气与阶梯碳交易的综合能源系统低碳经济调度模型,实现了系统经济性与低碳性的提高。
各类储能系统能够用于改善可再生能源的波动及平缓负载波动[10-12]。在评估储能系统的功率响应能力时,Wang等[13]评估了各种储能技术处理IES中波动和不确定性的能力,评估结果表明,单一类型的储能系统只能解决有限的波动场景。Wang等[14]通过创建两阶段混合整数非线性规划优化模型,实现了最大限度地降低多储能配置的总成本,优化了IES中混合储能的容量分配。Zhang等[15]开发了包含存储容量分配和操作优化的双层优化模型,并且使用置信区间使总规划成本最小化。Heidari等[16]构建了一个IES的随机优化模型,该模型具有基于价格的需求响应(DR)和冰存储,然后将其作为混合整数非线性规划问题求解。郭宴秀等[17]考虑了共享储能接入,优化了IES内部机组的能量交互,实现了系统整体运行成本优化。
基于以上研究背景,智能优化算法存在可解释性差,容易陷入局部最优等问题,而采用Karush-Kuhn-Tucher(KKT)条件与大M法将双层优化问题降维转化为混合整数线性规划(MILP)问题,能够有效地提取具有合理计算复杂度的系统特征,实现复杂问题的快速求解[18]。通过多类型储能技术实现可再生能源的消纳,同时考虑整个系统的低碳效应,笔者采用两阶段混合整数非线性规划优化模型构建了一种考虑协同低碳的多类型储能-综合能源系统双层优化调度模型。
1 多类型储能-综合能源系统模型
MTES-IES结构示意图见图1,系统包括3个模块:能量供应模块、能量转换模块和能源需求模块。该系统中主要包括风电(WT)机组、光伏(PV)机组、热电联产(CHP)机组、燃气锅炉(GB)机组、电解槽(EL)机组、燃料电池(HFC)机组、电-热-氢储能系统。通过多类型储能系统高效地平抑功率波动,实现负荷的时空平移,通过热电联产机组实现了电、气、热之间的能量耦合,构建了燃气锅炉机组的气、热耦合模型。针对风电的随机性与反调峰特性,在MTES-IES模型中构建风电-电解槽-储氢罐-燃料电池系统作为电-热-氢能源枢纽,针对电解槽-燃料电池耦合系统进行更精细化地建模,实现异质能量梯级转化、高效利用。
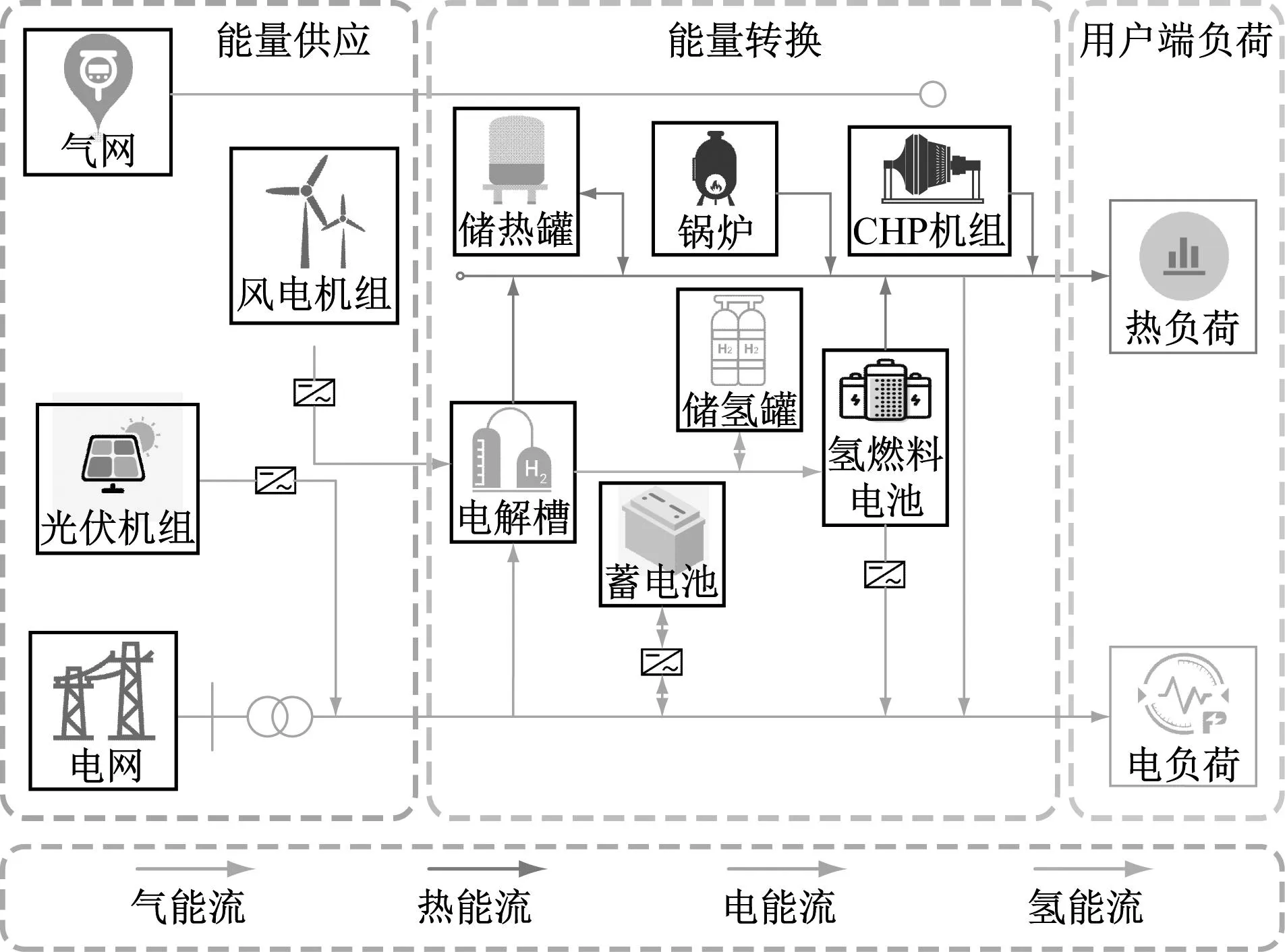
图1 MTES-IES结构示意图
2 多类型储能-综合能源系统双层优化
2.1 双层优化理论
双层(B-L)优化是指具有2个层次系统的优化,并且上层模型与下层模型之间存在耦合关系。通过B-L优化理论能够有效解决涉及多决策层与多主体利益的问题。在B-L优化模型中,上层模型与下层模型都有独立的决策变量、约束条件和目标函数。上层模型对决策进行优化排序之后做出决策,将决策变量传递给下层模型,然后下层模型在上层模型的基础上确定可行域范围,通过计算求解得到下层目标函数的最优解,再将下层优化结果反馈给上层模型,最后通过迭代得到其对应的最优解。B-L优化模型的数学描述[19]为
(1)
式中:x、F(x,y)、H(x,y)和G(x,y)分别表示上层模型的决策变量、目标函数、等式约束和不等式约束;y、f(x,y)、h(x,y)和g(x,y)分别表示下层模型中的决策变量、目标函数、等式约束和不等式约束。
2.2 上层多类型储能优化模型
针对上层模型,从多类型储能系统运营的经济性出发,综合考虑维护成本、充放电成本、储能市场补贴等经济性因素,最终求解规划期内多类型储能系统运行成本的最优解,决策变量包括电储能、热储能、氢储能系统的充放电功率。
2.2.1 上层优化目标函数
多类型储能系统中主要包含电储能、热储能、氢储能。多类型储能系统通过参与能源市场交互、储能政策补贴进行经营。上层目标函数可以表示为
minC1=COM1+CINA
(2)
式中:C1为储能系统运行成本,元;COM1为储能系统运行维护成本,元;CINA为储能系统参与能源市场交互成本,元。
储能系统运行维护成本为
(3)
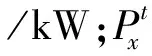
储能系统参与能源市场交互成本为
(4)
式中:Cx为第x台储能设备参与市场运行交互成本,元/kW。
2.2.2 上层模型约束条件
储电与储氢单元是由多块锂电池和储氢罐组成的集群,由于锂电储能(EES)与氢储能(HES)的约束相似,因此对二者进行同一化建模。建立热储能的灵活调节方式、布置合适的储热设备能够充分提高热能利用率,由于热储能(TES)系统存在差异,因此单独对其进行建模。在所构建的综合能源系统中,各个多类型储能子系统数学模型公式为
(5)
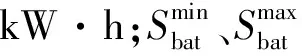
(6)
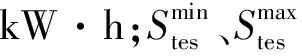
分析多类型储能系统运行的约束包括连续性变量与0-1型变量,为了降低非线性约束的求解难度,本文提出一种基于大M法的约束嵌套方案来解耦约束。将式(6)中第4、5数学模型表达式转化为
(7)
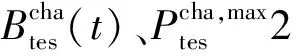
2.3 下层电-热-气-氢综合能源系统优化模型
针对下层优化模型,综合考虑多类型储能与低碳优化协同的IES优化运营,采用整个IES运营的经济性最优为下层目标函数,充分考虑IES的电、热、气、氢功率平衡和各项能源转换设备安全运行等约束条件。
2.3.1 下层优化目标函数
下层目标函数可以表示为
minC2=COM2+CG,B+CCT
(8)
式中:C2为综合能源系统运行成本,元;COM2为各个机组运行维护成本,元;CG,B为购电、购气成本,元;CCT为碳交易成本,元。
运行维护成本为
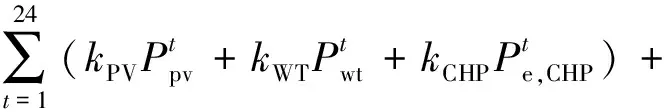
(9)
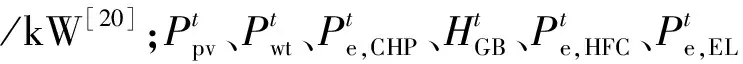
IES与电网、气网之间的交互成本为

(10)
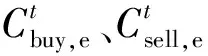
不同能源设备具有一定量的初始免费碳配额。基准碳交易成本是在固定碳交易价格下,根据实际碳排量与初始免费碳配额的差值计算所得。双向碳交易模式如图2所示。当系统碳配额不足,无法满足自身需求时,需要向碳交易市场购买碳配额;反之,当系统碳配额富余时则可向碳交易市场出售碳配额以获取低碳收益。
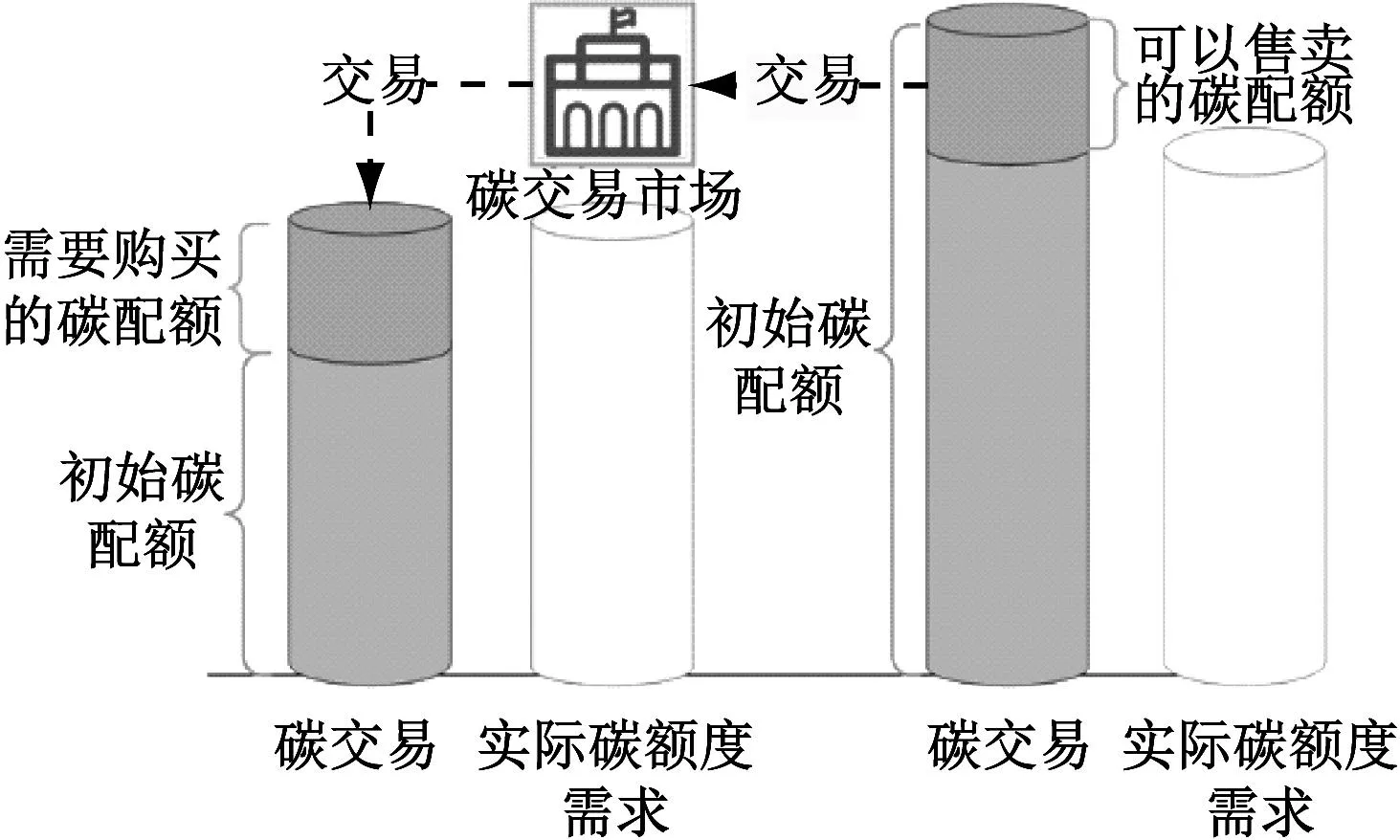
图2 双向碳交易模式示意图
综合能源系统中的碳排放综合考虑电网购电、热电联产机组及燃气供热锅炉机组,计算公式[20]为
(11)
(12)
(13)
式中:Cgrid、CCHP、CGB分别为电网购电、热电联产机组及燃气供热锅炉机组的初始碳配额,t/h;αe为单位电力碳配额系数,0.728 t/(MW·h);αh为单位热力碳配额系数,0.102 t/GJ;αe,h为单位电力与单位热力之间的转换参数,6 MJ/(kW·h)。
(14)
(15)
(16)
式中:Cgrid,a、CCHP,a、CGB,a分别为电网购电、热电联产机组及燃气供热锅炉机组的实际碳排放,t/h;βe为实际单位电力碳排放系数,1.08 t/(MW·h);βh为实际单位热力碳排放系数,0.065 t/GJ。
CCT=c(Cgrid,a-Cgrid+CGB,a-CGB+CCHP,a-CCHP)
(17)
式中:CCT为最终碳交易成本,元;c为碳交易基准价格,0.25元/kg[21]。
2.3.2 能源供应平衡约束
下层优化模型中主要包括能源功率平衡约束、能源供应设备运行约束、与电网功率交互约束、能源转换约束等。式(18)为系统电力平衡约束,式(19)为热力平衡约束,式(20)为氢平衡约束,式(21)为氢能枢纽能量平衡约束。
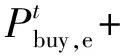
(18)
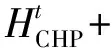
(19)
(20)
(21)

2.3.3 热电联产机组运行约束
(22)
(23)
(24)
(25)

2.3.4 燃气锅炉机组运行约束
(26)
(27)
(28)

2.3.5 电解槽-燃料电池耦合机组运行约束
不同于电化学储能,氢储能系统既能参与电网交互,也能同时参与热网循环。在整个风电-电解槽-储氢罐-燃料电池系统中,将风电产生的电能输入电解槽,通过电解槽热交换器使电解质与循环水进行热交换,从而实现热量供给。同时,将生成的部分氢气分配至储氢罐进行存储;再将部分氢气输送至燃料电池阳极,氢气在阳极通过覆盖有催化剂的质子交换膜被催化分解为质子,这些质子通过质子交换膜到达阴极。氢气在分解过程中释放出电子,通过负载将引至阴极发电。在阴极,质子与氧、电子结合生成水。燃料电池反应产生的水和热量通过气体扩散层从系统中排出,热水直接进入热水网络,参与热循环以满足热负荷需求[22]。
(29)
(30)
(31)
(32)
(33)
(34)
(35)
2.3.6 风电机组运行约束
(36)
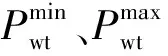
2.3.7 电网功率交互约束
(37)
(38)
(39)
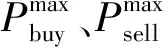
2.3.8 基于KKT条件与大M法的双层模型求解
在构建的MTES-IES双层模型中,上层模型针对多类型储能最优运营进行求解调度,下层模型在协同低碳运行的情况下进行最优求解。上、下层系统分别拥有各自的决策且相互影响,以多类型储能系统与综合能源系统两者实现自洽为前提,最终实现整个系统的最优调度。在调度过程中,双层模型耦合下的计算迭代涉及上、下层变量的传递,计算方法较为复杂,因此采用KKT条件与大M法对双层模型进行降维、线性化处理。图3为双层优化模型求解示意图。
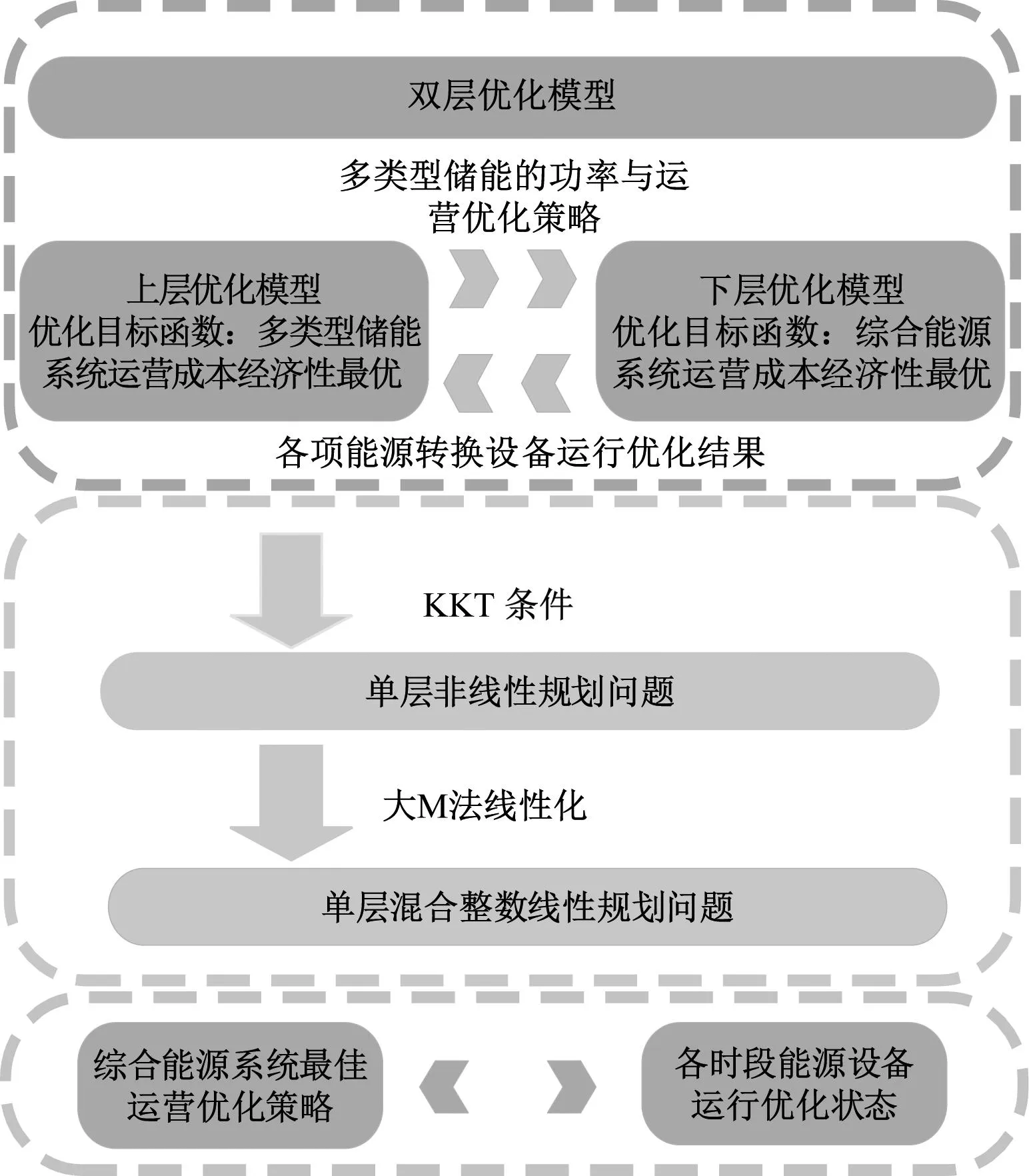
图3 双层优化模型求解示意图
KKT条件是拉格朗日乘子法的广义化,也是凸约束问题得到全局最优解的充分必要条件。因此,首先采用KKT条件对拉格朗日函数求解转化,再采用大M法线性化进行求解,模型求解转换思路可分为以下3个部分。
(1) 提出协同低碳的MTES-IES双层经济优化模型,确立上层多类型储能系统的经营优化与下层综合能源系统的低碳调度策略。
(2) 构建模型所需的拉格朗日函数,利用KKT条件将下层模型转化为上层模型的约束条件,采用大M法进行线性化处理,最终实现双层模型的降维处理。
(3) 在MATLAB平台中调用CPLEX求解,得到各时段异质能源流动调度状态,最终实现MTES-IES最优经营运行。
3 算例分析
MTES-IES双层经济模型由CHP机组单元、GB机组单元、EL-HFC耦合机组单元、WT机组单元、PV机组单元和MTES单元构成。在上层多类型储能系统最优经济性运行为主导、下层综合能源系统考虑低碳性的基础上进行经济优化调度,实现双层经济优化模型的自洽运行。系统根据各自最优成本优化各子系统供能策略。采用MATLAB 2023a建立优化模型,周期为24 h,步长为1 h,采用不同多类型储能系统配置与不同能量优化调度策略。
3.1 基本参数
算例中的过渡季节典型日负荷和风光发电功率预测数据选自我国西北某地,风电机组单机额定功率为30 kW,装机容量为210 kW,光伏机组单机额定功率为0.28 kW,装机容量为224 kW[23]。西北某地典型日电、热负荷需求和可再生能源发电情况分别见图4和图5。
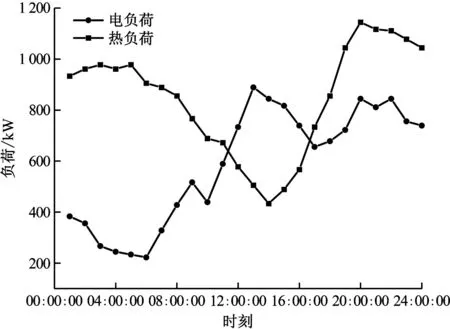
图4 电、热负荷需求示意图
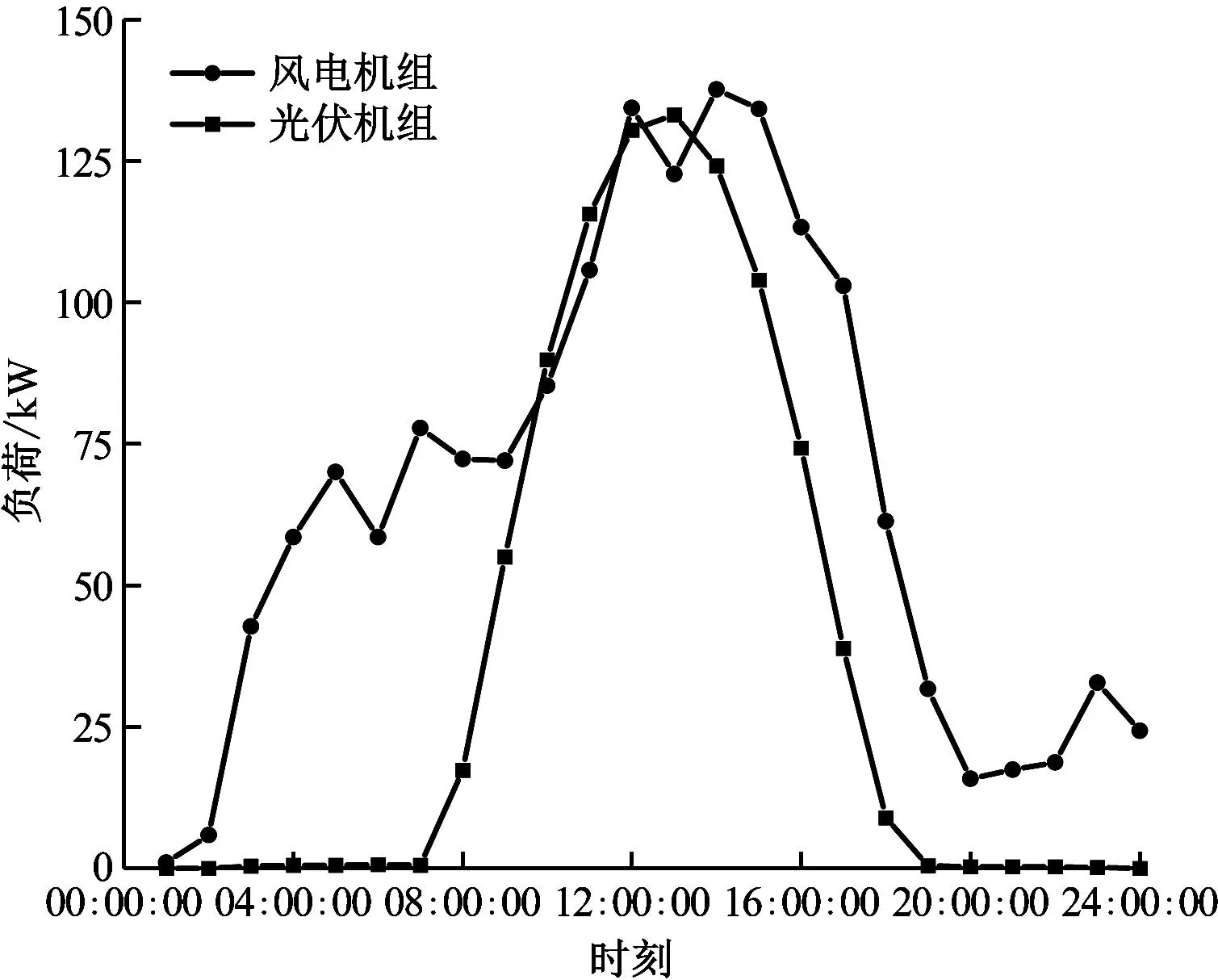
图5 可再生能源发电功率示意图
分时电价、气价是引导用户改变用能行为的重要措施,在构建的综合能源系统中加入分时电价、气价能够使系统在满足能量自洽的情况下,进一步实现各个能源子系统的最优经济性调度。详细分时电价、气价分别见表1和表2。
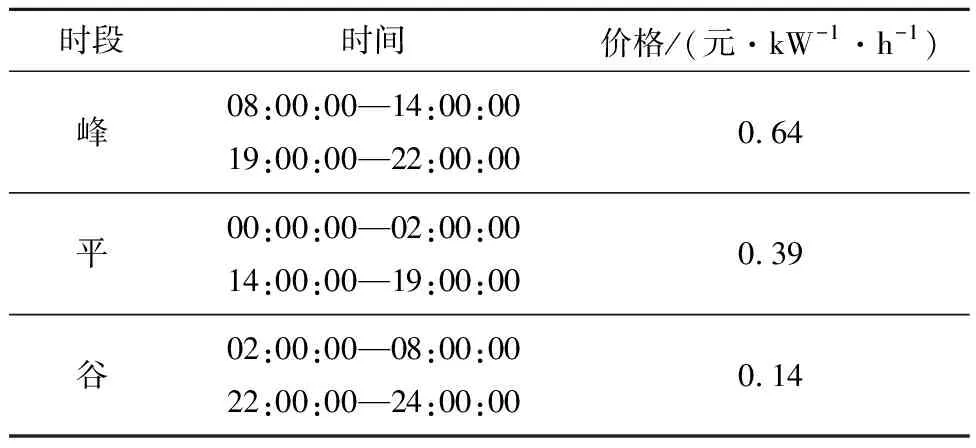
表1 分时电价

表2 分时气价


表3 能源设备参数[20-22]
3.2 不同场景结果分析
对比分析多类型储能协同低碳调度对综合能源系统的影响,以典型日负荷曲线和风电、光伏功率数据为支撑,设计了以下3个优化仿真场景进行计算。
场景1:仅考虑热、电储能接入,不考虑碳交易成本。
场景2:考虑风电-电解槽-燃料电池-氢储能耦合为能量枢纽接入,不考虑碳交易成本。
场景3:考虑电解槽-燃料电池-氢储能耦合为能量枢纽接入,同时考虑碳交易成本。
在场景1中采用传统电热储能系统双层优化调度模型,在场景2中将氢储能接入整个综合能源系统中,构建了风电-电解槽-燃料电池-氢储能耦合能量枢纽,充分实现能量梯级利用,在场景1、2中均不考虑低碳协同优化。在场景3的下层目标优化函数中增加了低碳协同优化目标函数以实现整个系统低碳调度。不同场景下各项成本参数及系统碳排放量对比分析如表4所示。

表4 不同场景中每日成本及碳排放量对比分析
由表4可知:在接入氢储能之后,运行过程中的余热被充分利用,碳排放量降低了2 278.6 kg;在此基础上采用低碳协同调度,通过对热电联产机组调度进行更加严格的限制,碳排放量进一步降低了2.91%,同时系统整体运行成本减少896.82元。
针对场景3中的供需结果进行详细分析。通过对多类型储能耦合综合能源系统进行24 h仿真调度,实现异质能源的最优化调度。系统根据各自最优成本优化各子系统供能策略,求解得到各子系统各时段优化调度出力,得到电、热负荷最优经济调度,分别见图6和图7。
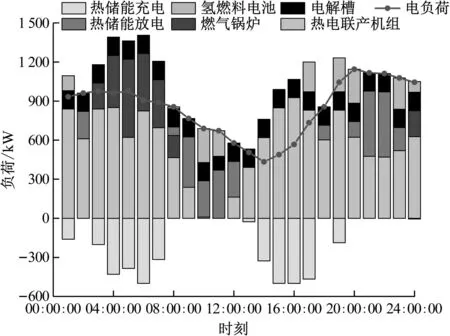
图6 电负荷最优化经济调度
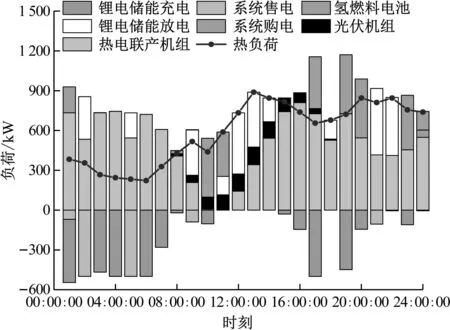
图7 热负荷最优化经济调度
通过最优负荷图像可知:电负荷与热负荷在时空上具有一定的互补性,在01:00:00—08:00:00之间,处于低电负荷与低电力价格时段,而此时用户端所需的热负荷较高。利用CHP机组的热电耦合特性,提高了GB机组的综合电热利用,剩余热负荷基本通过GB机组补偿。在08:00:00—14:00:00时间段,电负荷逐渐增加,热负荷需求逐步降低,此时通过CHP机组供应热量将使系统整体经济性降低,因此CHP机组与GB机组基本不再运行。根据储能系统低充高放的特性,在08:00:00—14:00:00时间段主要通过电储能与氢燃料电池供应电负荷,由于储能系统与氢燃料电池在运行过程中基本不会排放碳,因此该时段的系统基本实现零碳运行。在14:00:00—20:00:00时间段,电负荷呈平缓下降趋势,热负荷逐渐增加,由于CHP机组存在爬坡功率约束,仅能逐步增加输出功率,电负荷不足部分通过储能系统与电网购电进行补充。在20:00:00—24:00:00时间段,系统电、热负荷需求都趋于平缓,该时段CHP机组功率降低,HFC机组、EES出力逐渐增加,将多余电力部分向电网出售。
氢能作为综合能源系统中的能量转化枢纽,在经济性最优的前提下实现了可再生能源的消纳,并转化为电能、热能以满足系统的能量供应,同时降低CHP、GB等高碳排放机组的运行功率,实现整个综合能源系统的低碳经济调度。氢负荷平衡和氢能枢纽中心优化调度示意图分别见图8和图9。EL机组在24 h内实现了满负荷运行,消纳了全部可再生能源。同时由于CHP、GB机组都有爬坡约束限制,因此HFC机组在9:00:00—11:00:00、17:00:00—20:00:00和23:00:00—24:00:00时间段的出力较大,从而满足系统对电力、热力的需求。
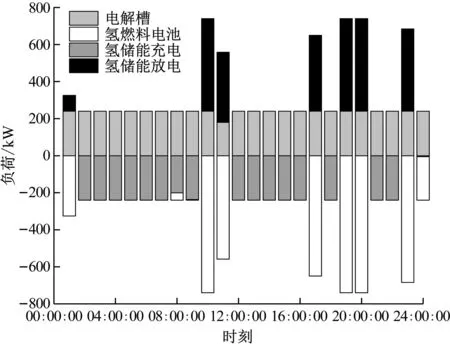
图8 氢负荷平衡
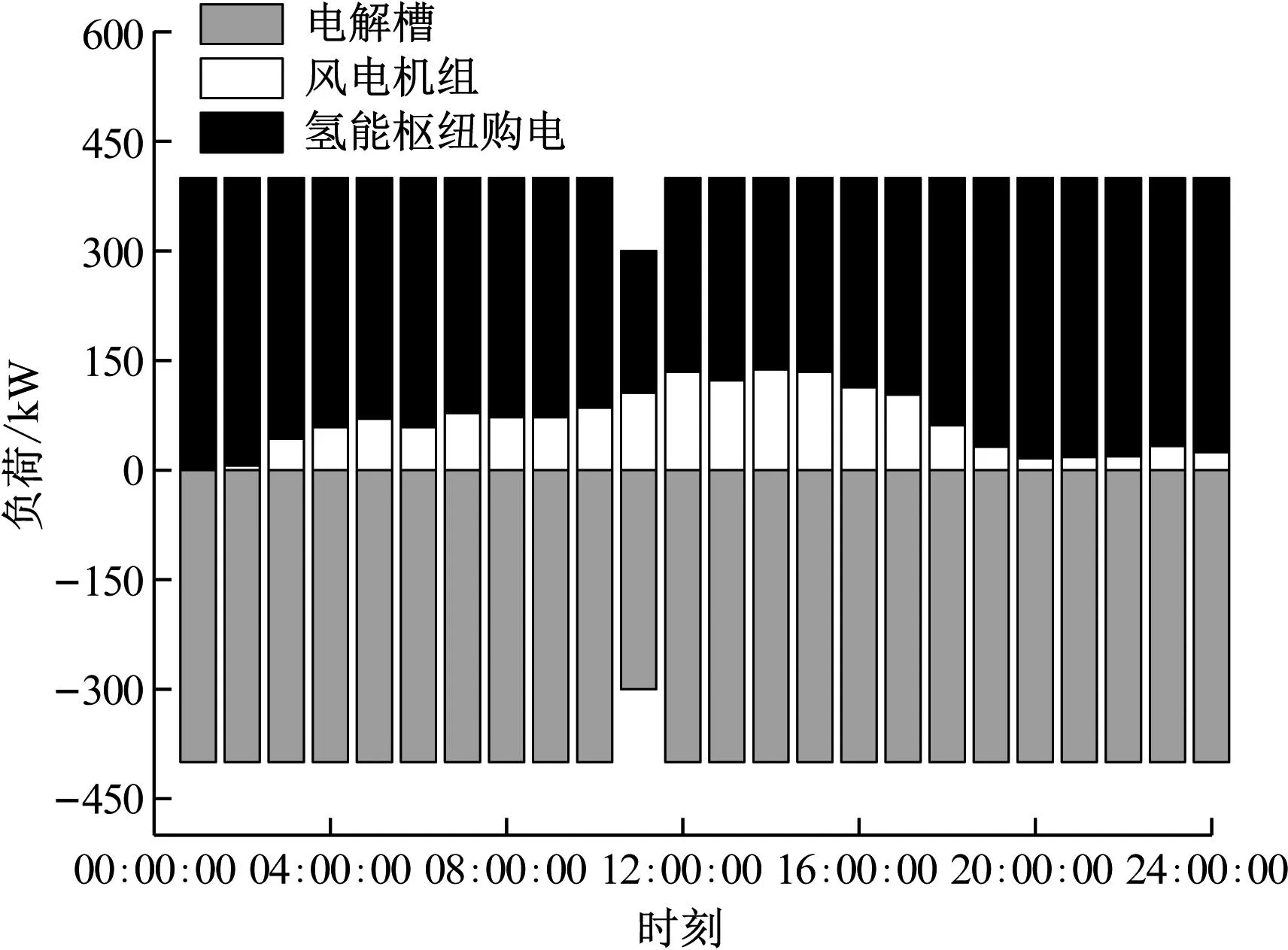
图9 氢能枢纽中心优化调度
图10为双向碳交易分时交易成本的结果。在双向碳交易模式下,下层模型充分实现了系统的低碳优化调度。在00:00:00—09:00:00时间段,可以通过向碳交易中心出售多余的碳配额来获取收益。在10:00:00—13:00:00时间段,由于机组热力负荷逐步下降,CHP机组出力逐渐增加,GB机组出力逐渐降低,碳交易中心分配给系统的碳配额不能满足机组碳排放需求,所以系统将向碳交易中心购买碳额度以满足自身需求。在14:00:00—24:00:00时间段,热负荷需求与电负荷需求不断增加,通过双层经济优化调度模型,在充分实现系统低碳调度的情况下,将多余碳配额出售给碳交易中心,进一步提高MTES-IES的经济性。

图10 双向碳交易分时交易成本
3.3 储能系统荷电状态分析
多类型储能系统的荷电状态(SOC)经济优化调度见图11。

图11 多类型储能系统SOC经济优化调度示意图
分析EES系统可知:在00:00:00—08:00:00时间段,电价处于平、谷段,EES系统主要进行充电,系统SOC逐渐增加;在09:00:00—14:00:00时间段,随着电负荷需求逐步增加至峰值的过程中,EES系统在满足电力需求供应的条件下,实现经济性最优调度,系统SOC处于波动状态;在15:00:00—19:00:00时间段,电负荷需求呈下降趋势且电价处于平价阶段,EES系统将电能储存,系统SOC逐渐增加;在19:00:00—24:00:00时间段,电负荷需求处于高位波动状态,电价处于峰值阶段,系统SOC逐渐降低,EES系统在满足系统电力供应平衡的情况下实现经济性运营最优调度。
分析TES系统可知:由于下层模型考虑协同低碳调度,碳交易中心对GB机组的碳配额相对较高,因此在00:00:00—08:00:00时间段,天然气价格处于谷底阶段,下层模型通过博弈计算决策,充分调动TES系统进行充电;在09:00:00—14:00:00时间段,用户端热负荷需求逐渐降低,此时能源价格上升,采用GB机组进行热供能将不再是最优决策,结合上层模型中TES系统经济性协同优化,该时段TES系统放热基本为全负荷运行,将释放上个时间段存储的热能;在15:00:00—19:00:00时间段,热负荷逐渐增加,将储存部分富余热能;在18:00:00—24:00:00时间段,热负荷需求较高,TES系统将储存的热能释放,以满足负荷需求且实现系统在双层优化下的经济性最优。
分析HES系统可知:在00:00:00—09:00:00时间段,HFC机组没有运行,因此HES系统一直处于充电状态;在10:00:00—15:00:00时间段,HFC机组供应电负荷、热负荷,同时将氢能逐渐释放出来;在16:00:00—19:00:00时间段,电负荷需求相对较低,因此HES系统又逐步充电,并且该时段天然气价相对较低,可将多余能量转化存储在HES系统中;在20:00:00—24:00:00时间段,电负荷、热负荷需求都相对较高,此时将氢能通过HFC机组转化为电能、热能以供应负荷需求。
由图11可以清晰看出,电、热、氢储能系统均在24 h内实现了“两冲两放”,基本符合储能系统在实际中的运行情况。
3.4 储能系统初始SOC
不同气候条件等因素影响可能造成储能系统初始SOC存在差异。由于外部环境对锂电储能系统影响较大,因此仅分析锂电储能系统不同初始SOC对整个系统的低碳经济运行调度策略的影响,结果见图12。
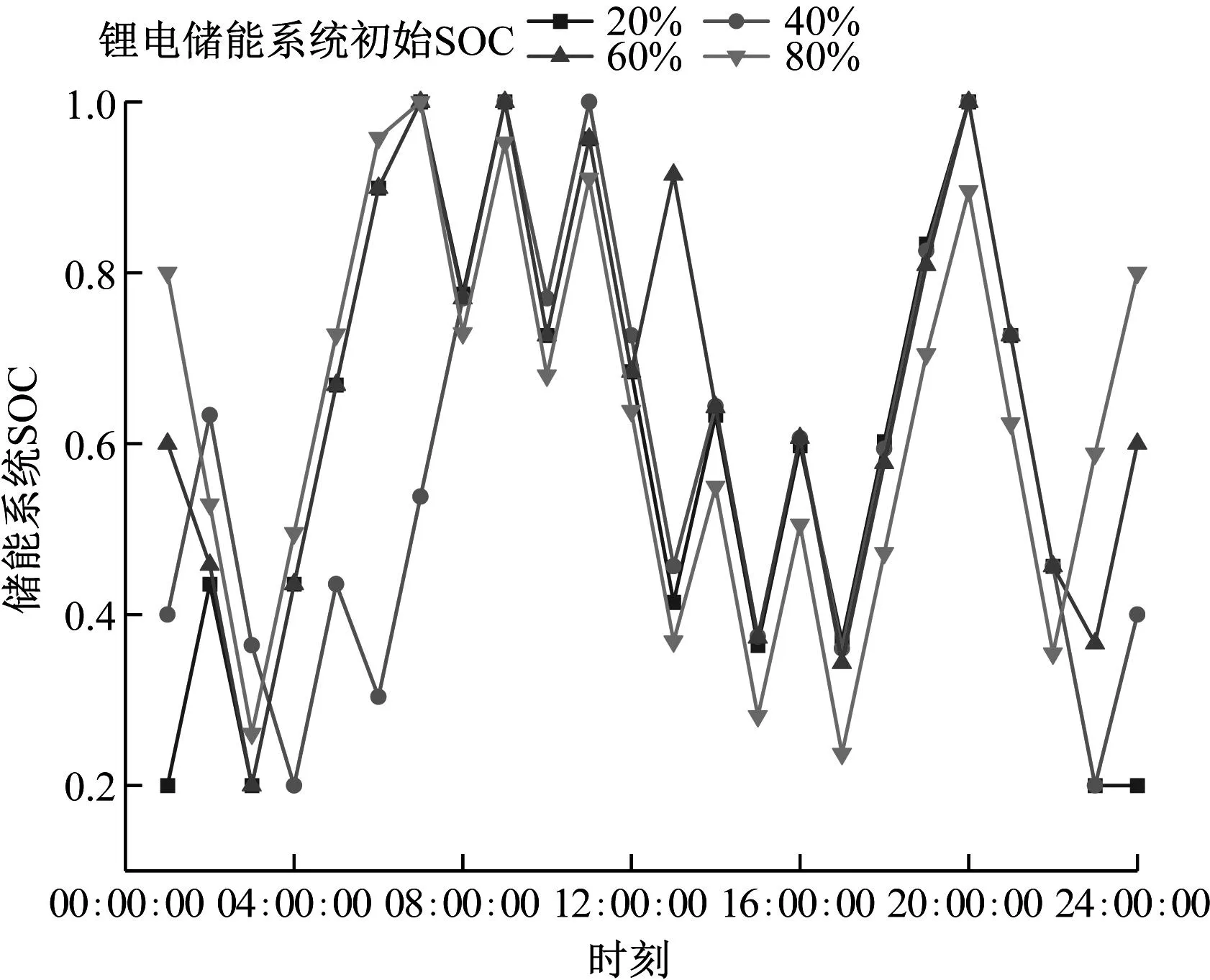
图12 锂电储能系统初始SOC影响分析示意图
EES系统运行主要受分时电价、天然气价等相关经济因素影响,在初始SOC改变的情况下,该系统中不同时段的充放电行为基本一致。在初始SOC低于0.4时,系统在初始情况下优先进行充电;初始SOC在0.6以上时,系统优先进行放电。因此,电储能系统的SOC存在最优解。通过对多类型储能系统进一步优化仿真,得到多类型储能系统最优初始SOC,如图13所示。
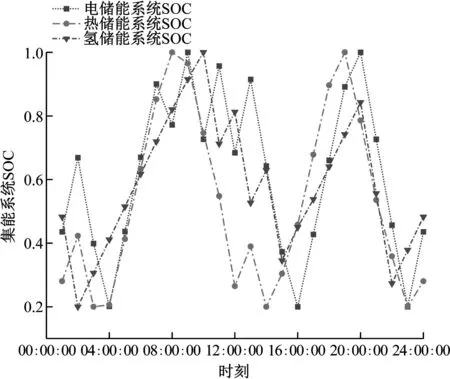
图13 多类型储能系统最优初始SOC运营示意图
根据仿真结果可知,多类型储能系统存在最优初始SOC,最优值受各类型负荷需求、能源价格、能源系统运行成本等相关参数的影响。后续将在此基础上增加时间尺度,进行各类型负荷预测,考虑可消减负荷等因素影响,从而引导储能系统进行最优经济调度。
4 结论
(1) 在上层多类型储能优化调度模型中,加入氢储能系统可以充分消纳可再生资源,构建风电-电解槽-燃料电池能量枢纽中心,充分利用电解槽、燃料电池在制氢、用氢过程中产生的余热,实现了异质能量的充分利用。
(2) 将低碳调度模型加入下层综合能源系统优化模型,在平衡负荷需求的情况下,各个子系统实现了低碳优化调度。对比分析可知,场景3在场景2的基础上碳排放量进一步降低了2.91%。
(3) 提出了一种基于电-热-气-氢联合协同低碳的双层经济优化模型,该模型实现了在低碳调度下多类型储能系统与综合能源系统不同利益主体的互利共赢,有效提高了供能品质。
