鱼类叉状尾鳍效率转捩点水动力性能研究

熊仲营,刘越尧

(江苏科技大学 船舶与海洋工程学院,江苏 镇江,212100)

0 引言

在逃避捕猎者、追捕猎物和迁移的自然选择压力下,鱼类已经演化出优秀的水下机动性能[1],其中鲔科为身体/尾鳍(body and caudal fin,BCF)游动模式鱼类,具有较高的游动速度和游动效率,因此成为了仿生水下机器鱼的理想生物原型。这种能力激起了更多工程师和研究者去研究其游动推力、阻力、功率消耗、效率和机动性能的潜在机理。鲔科鱼类的推动方式可归纳为基于尾鳍的升力基法,而尾鳍的形状差异性也被认为是不同游动行为的主要决定因素之一。

对于一个优秀的仿生自主水下航行器(autonomous undersea vehicle,AUV)而言,寻求一个有利的仿生尾鳍推进器是工程应用的关键。然而,Salazar 等[2]认为现代的机器鱼仍然不能复制特定鱼类的机动性特征,且缺少有效率的推进器。Yu等[3]认为目前仿生水下航行器样机尚无法做到内在机理上的相似,造成性能偏差的主要原因是对鱼体的主动驱动特性和流体控制机制尚不清晰,从而制约了仿鱼形水下航行器的高效推进性能。在这方面,一个优化或理想的尾鳍形状已经变成许多学者追求的目标[4-5]。Webb 等[6]总结了带有不同形状尾鳍的形式和功能差异,例如,带有窄尾柄的叉状或者半月形尾鳍能够提供加强型游动经济性。Low 等[7]发现即使低长宽比尾鳍具有较大的鳍面面积,但带有较高长宽比的尾鳍能在产生每单元推力和升力的同时引起较小的阻力。另外,Geder 等[8]研究了尾鳍鳍面面积对推进力的影响,得出当鳍面面积增加3 倍时,推进力增加了9 倍。Borazjani 等[9]发现在鸟和昆虫飞行中翼的前缘涡的再附着也发生在类鱼类游动中,许多鱼类的游动是通过身体波动带动尾鳍摆动实现推进运动,并证实了波动速度比游动速度更高,这个过程可以抑制沿鱼体的流动分离,且有助于前缘涡的再附着。Krishnadas 等[10]总结出尾鳍的推力主要源于推动流体向下流运动而产生的附加质量力、涡增推力和产生的前缘涡。Xiong 等[11]研究了摆动尾鳍前缘涡的产生和攻角之间的关系。然而,这些研究成果并没有充分考虑前缘涡诱导产生的涡增推力对总推力的贡献度,且尾鳍推进机理的研究又受限于尾鳍形状的多样性,因此这些研究是不充分的。

尽管学者们付出了许多努力,但尾鳍形状对于推进力性能的影响并没有被完全揭示[12-15]。在最近几十年内,生物推进的研究领域已经进行了许多基于计算流体动力学的数值研究和采用数字粒子图像测速(digital particle image velocimetry,DPIV)方法的实验研究。然而,当进行DPIV 实验研究时,由于分辨率或者光线限制的缘故,一些关键领域通常呈模糊状态,比如摆动尾鳍的前缘附近区域[9]。因此,更多研究关注在尾鳍的尾迹区域。但是,计算流体动力学仿真能够可视化这些关键区域的流动特性,并可检测潜在的流动机理。为了更好地识别尾鳍形状对于推进性能的影响,有计划地改变类鳍推进器的平面结构是一种常见的方法。然而,尾鳍的前缘和后缘也分别能够影响推进性能,这就难以对鲔科鱼类叉状尾鳍的推进性能提出归一性的评估方法。

文中为了研究叉状尾鳍效率转捩点的特征,将对推力产生和功率消耗的源项进行重点分析,目的是得出鲔科鱼类叉状尾鳍的高效推进内在作用机理,为水下仿生机器鱼推进器的设计和优化提供参考。

1 计算模型及研究方法

1.1 计算模型

为了揭示叉状尾鳍效率转捩点的特征,采用3 种鲔科鱼类叉状尾鳍结构模型,分别命名为Model-1,Model-2 和Model-3,从形态上分别类似于鲔鱼、扁舵鲣和灰跃鲣,如图1 所示。

图1 尾鳍模型和扫掠角定义Fig.1 The shape of the three caudal fin models and the definition of the sweep angle

图1 中,3 种模型的最大弦长分别为0.1 m、0.073 3 m 和0.126 7 m。更多的几何特征数据见表1,其中Sr2和Sr3分别为无量纲化2 阶矩面积和3 阶矩面积,定义为

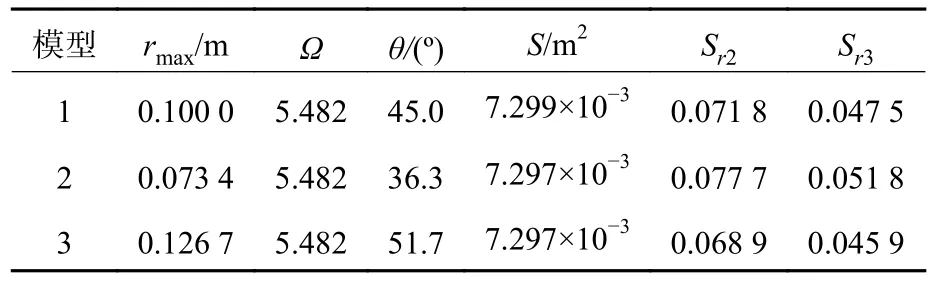
表1 3 种模型的几何参数Table 1 Geometric parameters of the three models

式中:r为尾鳍任意前缘位置到俯仰轴之间的距离;rmax为尾鳍弦向顶点与俯仰轴之间的距离,其值等于弦长c;S为尾鳍表面积;θ为扫掠角,定义为前缘顶点到后缘展向顶点之间的连线和俯仰轴之间的夹角。

从上表可以得出,3 种尾鳍具有相同的表面积、展弦比Ω和叉长b。这种布置形式显示了尾鳍除了弦向长度不同外,具有明显的相似性。不同的扫掠角虽然对应不同的弦长,但3 种尾鳍的扫掠角一旦被确定,其前缘和后缘形状也相应地被确定下来,因此叉状尾鳍的外形平面结构也就被确定。为了统一尾鳍形状的尺度,选取扫掠角来表征3 种不同的叉状尾鳍结构。另外,这种几何结构也确定了任意展向水平下都具有相同的从前缘到后缘的下游面积,从而使前缘涡的演化过程具有相同的激活时间。因此,这3 种尾鳍模型均较好地满足了控制研究要求的形状孤立因素。

1.2 运动模型

鲔科鱼类叉状尾鳍的运动形式可设定为沉浮-俯仰运动,表示为

式中:h为沉浮运动位移;Ψ为俯仰角,幅值为Ψ0;h0为尾鳍沉浮运动的幅值,其数值等于尾柄末端的波动幅值;ω为尾鳍摆动角频率;沉浮-俯仰运动之间存在着运动滞后,即存在相位差φ,全文取φ=90°。文中h0=0.05 m,Ψ0=25°。

决定推力和阻力的动量转换机制因素有: 雷诺数Re=Uc/υ,斯特劳哈尔数St=fA/U和尾鳍展弦比Ω=b2/S,其中,U为来流速度;c为弦长;υ为介质运动粘性系数;f为尾鳍的摆动频率,f=1 Hz;A通常被认为等于沉浮运动幅值的2 倍,即2h0,通过改变来流速度可获取不同的St。

Fx(t),Fy(t)和Mz(t)分别为瞬时推进力、瞬时侧向力和瞬时力矩,表示为

式中:nx,ny分别为鳍面沿x方向和y方向的法向单位向量;pn为尾鳍表面微元面积dS上的总压强。在1 个给定的摆动周期T内,尾鳍的平均推进力

尾鳍的平均输出功率为有用功率或推进功率,为

摆动尾鳍的瞬时总功率P(t)可以理解为灌输给尾鳍的用于克服流体力的总能量,目的是为了维持沉浮-俯仰运动,表示为

式中负号表示侧向力Fy(t)和绕俯仰轴的力矩Mz(t)是来源于流体介质的反作用力。1 个周期内的平均输入功率可表示为

从而,水动力推进效率η可定义为有助于推进的输出功率和总输入功率之比,即

1.3 仿真研究及网格无关性验证

在动边界流体域求解方法中,重叠网格技术可生成适合复杂几何边界的结构化网格,但频繁在重叠网格界面之间进行插值将对三维非定常流场求解的效率和准确性造成影响[16]。同时,采用浸入边界法对“锐边界”相关的动边界流动问题求解时,在浸入边界附近会出现违反几何守恒定律的情况,造成所谓的“伪”压力振动[17]。但是,贴体非结构化网格没有这些问题。

针对鲔科尾鳍的动边界摆动过程进行仿真,尾鳍的实际摆动运动通过ANSYS Fluent 软件的用户自定义函数(user define function,UDF)中DEFINE_CG_MOTION 宏进行规划,其可以预设叉状尾鳍摆动运动所包含的俯仰速度和沉浮速度。湍流模型采用了SSTk-ω模型,PRESTO!和QUICK 项则分别用于离散压力和力矩方程。计算区域尺度沿x,y和z方向分别设置为20c×10c×8c,尾鳍的前端端点到进口的距离为5c。计算域入口和出口分别设定为pressure-inlet 和outflow 边界条件,摆动尾鳍表面满足无滑移壁面条件,计算域的其他面则设定为symmetry 边界条件。

计算域内的网格划分采用非结构化网格,四面体网格用于空间离散三维计算域,并进行网格动态更新。网格无关性研究选取了4 种不同分辨率的网格作为研究对象,获取4 种分辨率网格主要是通过改变尾鳍表面的节点数和三维计算区域的单元数来实现,即增加尾鳍表面和尾鳍附近区域的节点和单元数,以及整个计算区域体的总单元数。4 种网格分辨率分别为36.9×104(Grid-1),58.2×104(Grid-2),12×105(Grid-3),和19.5×105(Grid-4)。网格无关性研究主要是通过检测平均推力系数和效率η随着总单元数的变化规律,如图2 所示。计算结果也显示了Grid-3 和Grid-4 之间具有较小的差异。更者,Grid-3 和Grid-4 时的平均推力分别为0.134 N 和0.132 N,相差3%。因此,选择Grid-3 作为三维数值仿真的网格量级。

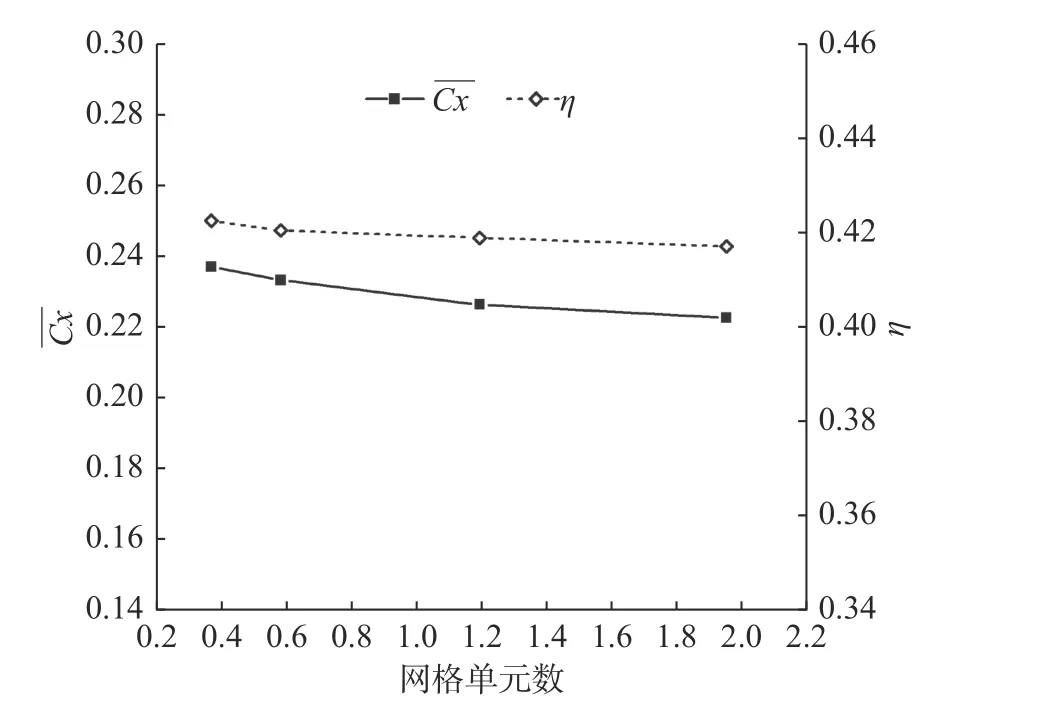
图2 平均推力系数和效率随单元数变化曲线(St=0.25)Fig.2 Curves of average thrust coefficient and efficiency with the number of units(St=0.25)

除此之外,图3 显示了所采用的Grid-3 和Grid-4 网格分辨率下的尾迹涡结构,并且发现在可见区域内尾迹发夹涡结构仅仅存在较小的差异。因此,三维模型所拥有的1.2×106网格单元量级对于尾迹涡结构研究是合适的,同时也证实了数值方法可以有效模拟鱼类叉状尾鳍摆动过程的水动力特征。

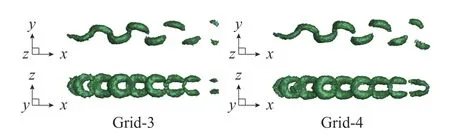
图3 2 种网格尺度下尾迹涡结构对比Fig.3 Comparison of wake vortex structures at two grid scales

为了避免过大的网格变形,甚至负网格单元体,时间步长通常由流动速度和尾鳍速度决定。依据一般的经验法则,在1 个给定时间步长内,尾鳍边界运动的距离需要小于最小单元尺度的一半。而文中三维仿真设定的时间步长为0.000 5 s,所采用的时间步长较好地满足了这一标准。因此,文中所选择的时间步长尺度是可以接受且可信的。

2 仿真结果及分析

2.1 推进效率与St 的关系

为了达到优秀的巡游推进性能,最好的方法是采用一种较高的游动效率。图4 显示了在St=0.2～0.3 范围内3 种尾鳍模型的推进效率。其中3 种模型的效率转捩点都在St=0.25 处获得,因此选取St=0.2～0.3 作为研究范围。从图4 可知,Model-3 在上述范围内具有较高效率,Model-2 的效率较小,而Model-1 则处于两者之间。

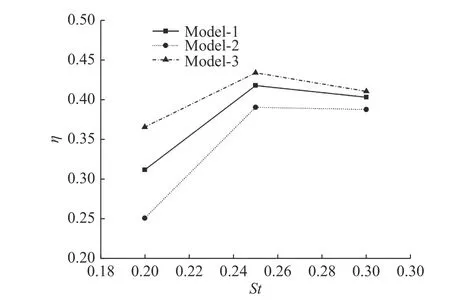
图4 3 种模型的推进效率(St=0.2～0.3)Fig.4 Propulsion efficiency of three models with St numbers in the range of 0.2-0.3

2.2 推进力和功率与St 数的关系

图5 和图6 分别显示了3 种尾鳍模型在St=0.2～0.3 范围内的时均推力和时均功率。值得注意的是,3 种模型的随着St的增加而增加,并且三者之间的差距在转捩点附近也变得越来越小。从图中可以得出Model-3 的增长率最低,而Model-2 最高。然而,3 种模型的时均功率曲线都一致地随着St的增加而增加。另外,从Model-3 到Model-1,再到Model-2,功率消耗在St=0.2～0.3 范围内连续增加。平均推力和功率的不同变化规律源于扫掠角的改变,也意味着来自前缘和后缘的差异,同时也可以看出影响平均推力和功率的源项是不同的。

图5 3 种模型的时均推力(St=0.2～0.3)Fig.5 Time-averaged thrust of the three models with St numbers in the range of 0.2-0.3

图6 3 种模型的时均功率(St=0.2～0.3)Fig.6 Time-averaged power of the three models with St numbers in the range of 0.2-0.3

对于St=0.2～0.3,Model-3 具有较高的效率,但是推力并不总是最大的,特别是在较高的St情况下。另外,Model-2 具有最低的效率,但却有在较高St下较好地产生推进力的潜力。Model-1 则是处于两者之间的中间状态,具有较高水平的推力和效率值。

2.3 叉状尾鳍推力和功率的源项分析

Krishnadas 等[10]将尾鳍的推力F推力分解为附加质量力F附加质量力、涡增推力F涡增推力和前缘涡吸力F前缘吸力。前缘涡吸力是指在尾鳍前缘由于涡的分离造成的负压。由于前缘涡量较小,因此前缘涡吸力通常相对较小。但随着前缘涡不断在尾鳍吸力面延伸、发展和脱落,在吸力面形成的负压将会逐步增大从而形成涡增推力。附加质量力是由于尾鳍的压力面推动流体向下流运动而产生的流体附加质量力,同时该附加质量力也会对尾鳍形成反作用力,即附加质量力实际为摆动尾鳍受到流体的反作用力。摆动尾鳍的推力可表示为

对于类似昆虫和以尾鳍等摆动运动的生物推进功能部件,其推力和功耗水平可用S×Sr2和S×Sr3来表征,且S×Sr2在本质上代表了尾鳍的“有效面积”。但对于不同的功能部件和运动方式的差异,S×Sr2和S×Sr3是否能表征叉状尾鳍的推力和功耗水平是需要验证的。图7 和图8 分别显示了在St=0.2～0.3 范围内推力和功率随着S×Sr2和S×Sr3的变化规律。从表1 中可以看出,Model-3 具有较大的扫掠角,但是它的S×Sr2和S×Sr3值却是最小的,Model-2 却恰恰相反,Model-1 则处于两者之间。因此,在图7 和图8 中每条曲线的纵坐标值是随着横坐标值从Model-3 到Model-1,再到Model-2 的过程而相应发生变化。在图7 中,在St=0.2 时推力随着S×Sr2值的增加而降低,而在St=0.25 时则近似呈水平状态,在St=0.3 时则有略微的增加,这种趋势显示有多种因素影响了推力的产生。由于Model-3 具有较小的有效面积,来自于流体的反作用力略小于其他模型。因此,对于Model-3在St=0.2 具有最大推力的唯一原因可能源于强烈的前缘涡和较大的涡增推力。另外,随着St的增加,源于尾迹的反作用力变得更大,并且反作用力的份额也变得更大。因此,在St=0.3 时推力随着S×Sr2值的增加而增加。图8 显示了在St=0.2～0.3范围内功率也随着S×Sr3值的增加而增加。另外,其增长率也随着St的增加而增加。尽管由于横坐标值差异较小造成可能的近似线性关系,但是推力和效率也并非分别与S×Sr2和S×Sr3值呈严格的线性关系。推力和S×Sr2值之间的非严格线性关系除了强烈的非稳态特征外,可能还源于在不同扫掠角下前缘涡的产生和发展的差异,以及St的不同。这是基于如下事实: 前缘涡的行为引起了不同的低压分布,影响了整个尾鳍表面的压力差。然而,功率和S×Sr3值之间的非线性关系可能主要源于在每个St下尾迹的强非稳态特征。很明显,产生推力的源项并不是唯一的,而S×Sr2仅仅反映了由于推动流体向下游运动而引起的对压力面的反作用力,即附加质量力。推力的其他源项将和前缘涡有直接关系,因此尾鳍前缘结构也是推力产生的主要影响因素之一。然而,S×Sr3则较好地反映了功率消耗的能力水平。

图7 推力相对于S×Sr2 的关系(St=0.2～0.3)Fig.7 Thrust as a function of S×Sr2 with St numbers in the range of 0.2-0.3

图8 功率相对于S×Sr3 的关系(St=0.2～0.3)Fig.8 Power as a function of S×Sr3 with St numbers in the range of 0.2-0.3

因此,增加扫掠角引起了较低的功率消耗,并获得了一个适中的推力。然而,尽管增加扫掠角可能导致功率消耗的降低,但过度增加扫掠角可能引起推力和效率的下降,特别是在较高St的情况下。

2.4 功率消耗评估

巡游游动时,将在y坐标方向和z坐标方向的速度平方分别命名为v2和w2,实际上意味着在相应方向的能量消耗。图9 显示了在St=0.3 的3 s时3 种尾鳍模型的v2+w2分别为0.003(蓝色区域)、0.01(绿色区域)和0.03(红色区域)的等值面图。结果显示,围绕3 种尾鳍的区域具有相似的功率消耗分布,且在3 种模型之间仍具有可辨识的差异。比如,Model-2 在尾迹区具有最高的功率消耗,Model-3 则最低,这种结果也证实了上述功率消耗的变化规律。

图9 3 种模型在3 s 时的能量消耗等值面图(St=0.3)Fig.9 Energy consumption contours of three models at 3 s(St=0.3)

2.5 叉状尾鳍尾迹射流特征

由尾迹涡所诱导的喷射流极大地决定了推力的产生。为了检测与喷射流相关联的流向方向的动量,在St=0.25 时3 种尾鳍模型流向方向的速度等值面如图10 所示。

图10 3 种模型尾迹流向方向速度的瞬态等值面图(St=0.25)Fig.10 Transient contours of wake flow direction velocity for three models at St=0.25

图10为3、3.16、3.32 s3 个时刻流向方向的速度等值面。其中,蓝色,绿色和红色区域分别表示高于自由来流速度的7.5%、15%和20%。由图可知,在St=0.25 时Model-3 所产生的喷射流在3 个时刻都是最弱的,这表现了相对于其余2 个模型,Model-3 具有较弱产生推力的特性,而这部分推力主要来源于推动流体向后运动产生的反作用力,实际上是由于较小有效面积所造成的。另外,Model-1 的蓝色面积大于Model-2,但是绿色面积却较少,因此,Model-2 具有较好的推力产生潜力,这也对应于其具有较大的有效面积。

如果巡游需要产生足够的推力,带有较低扫掠角的叉状尾鳍应当被选作为水下航行器的合适推进器。这是因为鱼类并不总是游动在较高效率区间内,但是却常游动在能够应付特定的或者复杂的游动环境下。即Model-2 在较高St条件下具有较好的推力产生潜力。相反,具有较大扫掠角的叉状尾鳍能够提供较高效率的游动性能,但却是以降低推力产生为代价。

2.6 摆动尾鳍表面压力分布规律

图11 和图12 分别为在St=0.25 和St=0.2 时3 种尾鳍模型在3.16、3.28、3.48 s 时刻的表面压力云图。前缘涡出现、发展并延伸到整个吸力面是在前缘涡从尾缘分离之前完成的,因此决定了吸力面的涡增推力分布。

图11 3 种模型在3.16 s、3.28 s 和3.48 s 的表面压力分布(St=0.25)Fig.11 Pressure contours of the three models at 3.16 s,3.28 s and 3.48 s at St=0.25

图12 3 种模型在3.16 s、3.28 s 和3.48 s 的表面压力分布(St=0.2)Fig.12 Pressure contours of the three models at 3.16 s,3.28 s and 3.48 s at St=0.2

在3.28 s 时,正压区域已经填满了整个压力表面。3 种尾鳍模型在压力面的高压在St=0.25 时比St=0.2 时占据了更大的面积。此外,在St=0.25 和St=0.2 时,Model-2 的高压面积大于Model-1,而Model-3 的高压面积最小。另外,越接近前缘端点,压力就越高。这种压力分布反映了不同有效面积的叉状尾鳍提供推进力的差别。而且,较高的沉浮速度也促使3 种尾鳍模型在此时获得了较高的压力。此外,3 种尾鳍模型的吸力面显示了前缘涡向下游平动,并且负压区域在Model-3 中传播得最远,而在Model-2 中则最近。这种负压区域的分布意味着Model-3 的前缘产生了最强的前缘涡,而Model-2 所产生的前缘涡是最弱的。

在尾鳍摆动过程中,大部分推力来源于在整个尾鳍表面贡献于推进方向分量的压力差。在3.28 s时,压力面具有较高的正压值,且吸力面也表现出一定程度的负压区域。配合较大的角位移,2 个表面之间的压力差导致了在3.28 s 附近产生了最大推力。因此,在接近3.28 s 时整个尾鳍表面的压力差较大程度决定了瞬态推力的幅值。另外,在St=0.2 的3.28 s 时,压力面显示了3 种尾鳍模型存在较小的压力差异。然而,Model-3 的吸力面具有较大的负压面积,从而导致了在St=0.2 时出现最大推力。甚至在St=0.2 的3.48 s 时,在压力面和吸力面之间存在较大的压力差也证实了这种说法。因此,尽管Model-2 带有较低的扫掠角,并且前缘涡产生得更快且发展得更早,但其前缘涡的强度却是最低的。再者,在St=0.25 的3.28 s 时,Model-2的压力面显示了更大面积的正高压,但是在吸力面则具有较小面积的低负压。Model-3 则正好相反,Model-1 则处于两者之间。在St=0.25 时的压力分布导致了3 种尾鳍模型具有较小的推力差别。

以上的分析说明了扫掠角的增加使得尾鳍的有效面积衰减,从而导致了源于推动流体向下游运动而产出的反作用力对于推力的贡献能力的退化。此外,扫掠角的增加也引起了前缘涡强度的增强和前缘涡的发展,从而导致了源于吸力面的低压区域涡增推力的增大。扫掠角对涡的演化特征的影响是复杂的,但却影响了推进力产生的幅值。扫掠角对附加质量力和涡增推力有相反的作用机制。

3 结论

文中对3 种鲔科鱼类叉状尾鳍的摆动过程进行了仿真,运动形式设定为沉浮-俯仰运动。3 种尾鳍具有相同的表面积、展弦比和叉长,其扫掠角表征了不同的叉状尾鳍平面结构。为了研究叉状尾鳍效率转捩点的特征,对推力和功耗的源项进行了重点分析,并对叉状尾鳍高效推进的作用机理进行了探讨。为了获得AUV 的优秀仿生推进器,叉状尾鳍的拓扑结构优化研究非常必要,也具有较好的工程应用前景。通过文中研究,可得如下结论。

1) 在保证尾鳍表面积不变时,增加尾鳍扫掠角时其2 阶矩面积(有效面积)随之降低,从而导致了尾鳍摆动时推动流体向下游运动而受到的反作用力降低,因此尾鳍的推进能力也会随之衰退。

2) 扫掠角的增加会引起前缘涡强度的增加以及前缘涡的发展,从而导致更大的涡增推力。因此,扫掠角对附加质量力和涡增推力有相反的作用机制。

3) 增加扫掠角造成了较低的功率消耗和适中的推力,产生推力的源项并不是唯一的,而3 阶矩面积则可直接用于评估功率消耗的能力水平。

4) 过分增加扫掠角尽管存在功率消耗下降的优势,但也引起推力和水动力效率的下降,特别是对于高St的情况;带有较低扫掠角的尾鳍具有最低的效率,但是却在高St情况下具有较好的产生推力的潜力。