波浪环境下无人水面艇改进MFAC 节能控制方法

2024-03-14魏佳广张拓圣辛筠炜李怀亮张西伟

水下无人系统学报 2024年1期

魏佳广 ,张拓圣 ,辛筠炜 ,李怀亮 ,张西伟

(1.海洋石油工程股份有限公司工程技术中心,天津,300461;2.哈尔滨工程大学智能海洋航行器技术全国重点实验室,黑龙江哈尔滨,15001)

0 引言

无人水面艇(简称无人艇)是一种漂浮在水面的小型智能平台,作为一种海洋智能装备,其具有环境适应力强、成本低、可搭载多种任务载荷等特点,对于充分利用海洋资源具有重要且广泛的应用价值[1]。

目前,无人艇的运动控制研究属于热点问题,主要的控制方法有比例-积分-微分(proportionalintegral-derivative control,PID)控制[2-3]、S 面[4-5]、神经网络[6-7]、模糊PID 控制[8-9]、自适应控制[10]、反步法[11]、滑模控制[12]、无模型自适应控制(modelfree adaptive control,MFAC)[13-14]、人工鱼群算法[15]、自抗扰控制[16]以及模型预测控制[17]等。由于受到外界环境扰动和模型摄动等不确定因素影响,无人艇的运动数学模型具有较强的非线性和耦合性,在设计过程中难以为控制器提供精准的数学模型[13]。因此,仅利用受控系统的离、在线输入/输出数据来设计控制器的数据驱动控制方法进入人们的视野中[18]。侯忠生等[19]提出了一种数据驱动控制方法——MFAC 方法,经过不断的发展和完善,已逐渐形成一套完整的控制理论体系。廖煜雷等[13]针对无人艇艏向控制子系统的特殊动力学特性,引入重定义输出增益,提出了重定义MFAC(redefine MFAC,RMFAC)方法,并通过仿真实验及外场试验验证了该方法的有效性和实用性。杜廷朋[20]针对使用标准MFAC 时无人艇出现的航向响应振荡、不能收敛的现象,提出了差分型MFAC和非增量型MFAC 方法,解决了标准MFAC 方法应用过程中存在的问题。

在运动控制方法研究的基础上,针对无人艇节能控制方法研究也不断展开。魏红艳[21]将无人艇路径跟踪滑模控制器与基于障碍李雅普诺夫函数的原理相结合,设计了无人艇区域保持控制器,同时设计了环境最优区域保持不连续控制器,从而减少了能耗,增加了推进器持续工作时长。周韬等[22]使用非线性反馈技术对航向保持控制进行优化,采用模糊PID 控制器对航向保持控制方法进行设计,仿真实验证明了其可行性。冯永孝[23]将非线性馈饰技术与模糊PID 控制器相结合,使控制性能得到提升,并在一定程度上减少了能耗。

上述文献在运动控制研究中大多实现了更快、更精确的无人艇运动响应,但是没有考虑运动控制过程中的能耗过大及设备寿命等问题。为此,文中首先建立无人艇运动数学模型和波浪干扰下运动力学模型;其次,设计了模糊RMFAC(fuzzy RMFAC,FRMFAC)方法;最后,对波浪影响下无人艇节能运动控制仿真进行研究,以验证控制器的节能控制效果。

1 无人艇运动数学模型及波浪干扰分析

1.1 运动数学模型

文中研究对象为船长5.2 m,排水量1 900 kg的喷水推进单体无人艇。建立其惯性坐标系OEXEYEZE和船体坐标系Ob-XbYbZb,各坐标系均按照右手法则设计,如图1 所示。

图1 惯性坐标系和船体坐标系Fig.1 Inertial coordinate system and hull coordinate system of ship

由这2 个坐标系可得无人艇的6 自由度运动数学模型,并简化为水平面3 自由度的运动数学模型[24]

式中:x,y分别为横向和纵向位移;ψ为艏向角；u,v分别为纵向和横向速度;r为艏摇角速度;Fu和Tr分别为纵向推力与转艏力矩;du、dv分别为波浪等环境干扰造成的横向和纵向干扰力;dr为环境干扰力矩。

该无人艇的运动模型参考文献[25],通过对其辨识得到的水动力系数进行适当选取与转化,得到文中的运动参数为: 船体坐标系中3 个坐标轴下的惯性系数m11=2.4×103kg、m22=3.35×103kg、m33=2.49×105kg;阻尼系数d11=255 kg/s、d22=2.92×103kg/s、d33=1.22×104kg·m2/s。

1.2 波浪对无人艇的干扰建模

真实情况下波浪是不规则的,通常采用相位调制(phase modulation,PM)波能谱密度函数公式对波浪进行建模[26]

式中: ω为波浪频率;hs为有义波高;g为重力加速度。

当hs=0.2、0.4、0.6m 时,对应的PM 波能谱密度曲线如图2 所示。

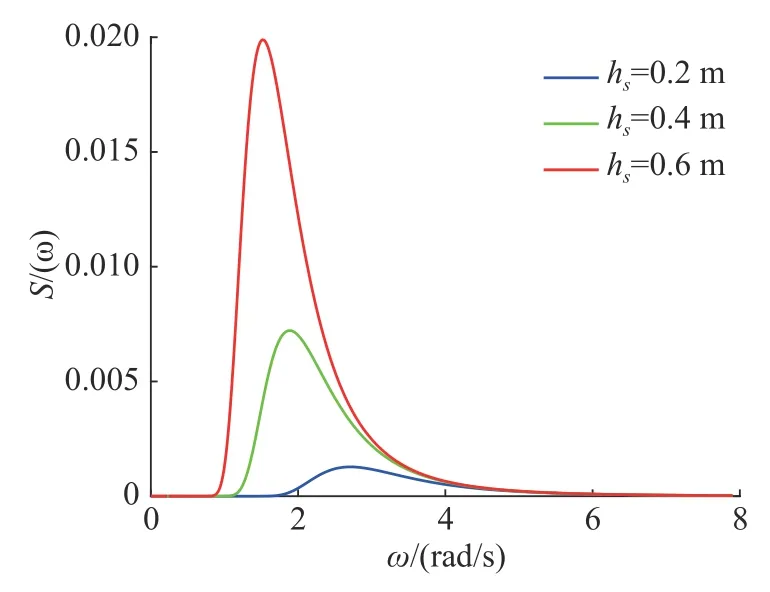
图2 PM 波能谱密度曲线Fig.2 Curves of PM wave energy spectral density

波浪扰动函数为

式中: ωi为第i个单元的特征频率;εi为[0,2π]上均匀分布的随机数;H(t)为实时波高。

hs=0.6 m时的波浪仿真如图3 所示(图中,H为波高)。

图3 实时波浪仿真Fig.3 Simulation of real time wave

使用Daidola 提出的对无人艇在波浪干扰情况下的受力计算公式对2 阶波浪力和力矩进行计算[26],由于实时波浪力计算十分繁琐,因此采用平均波高进行计算,其公式如下

由于无人艇顺浪与逆浪情况下遭遇角对称相等,仿真中的波浪方向恒定沿Y轴(惯性坐标系下)负方向;而无人艇艏向以Y轴正方为0 度,以逆时针方向为正,因此遭遇角 χ=|π -ψ|。

1.3 波浪影响下无人艇回转仿真实验

对无人艇在不同波浪情况下进行回转仿真。实验恒定推力Fu=500 N,恒定扭矩Tr=300 N·m,同时设定恒定的波浪方向沿Y轴负方向。仿真结果如图4 所示,图中星号为航行起点,三角箭头为终点。

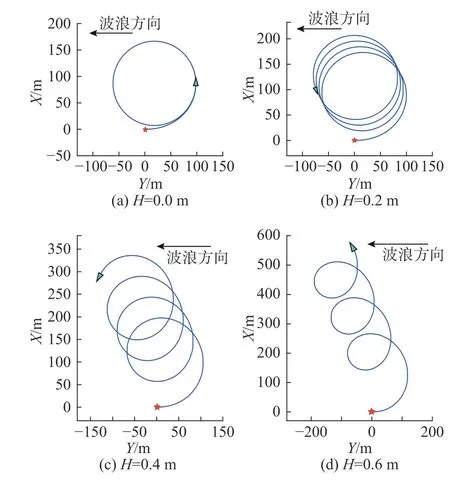
图4 不同波高时无人艇回转轨迹Fig.4 The rotation trajectory of the unmanned surface vessel at different wave heights

分析可知,在无人艇运动过程中,波高越大无人艇产生的扭转力矩越大,无人艇的航迹和偏移距离也越大。由于无人艇回转运动时艇体各方向都会受到波浪力的干扰,导致无人艇运动轨迹发生偏转的方向大致与波浪方向一致。

2 无人艇运动控制应用分析及方法设计

无人艇在不同波浪环境下运动时,固定的控制参数会造成控制响应趋于一致,但实际在顺浪和逆浪情况下无人艇对控制器响应速度的要求是不同的。顺浪情况下,控制器需要灵敏地作出响应,以防止偏离期望艏向造成较大误差;逆浪情况下,控制器可较为缓慢地响应,以节约能量消耗减少机械结构磨损。

文中针对无人艇在波浪环境中的艏向控制问题,基于RMFAC 方法[13],并结合模糊控制提出一种FRMFAC 方法,以使无人艇适应更多复杂海况。通过分析不同波浪情况及控制参数对无人艇的控制效果,设计相应的模糊控制规则。该方法可根据不同波浪环境对RMFAC 参数进行在线调整,在保证控制效果的基础上,达到节能的效果。

2.1 RMFAC 方法

考虑在无人艇艏向控制系统下,探究紧格式动态线性化MFAC(compact form dynamic linearization MFAC,CFDL-MFAC)方法[19]的应用问题,其控制方法为

式中:λ＞0为权重系数;y*(k+1)为期望输出;ρ ∈(0,1]。

式中: µ＞0为权重系数;η ∈(0,1]为步长因子;ε为1 个充分小的正数;(k)为ϕ(k)的估计值;(1)为ϕˆ(k)的初值。

式(8)是算法重置机制。该算法不包含任何模型信息,且对时变信息不敏感,算法的重置机制也提高了伪偏导数估计算法跟踪数据随时间变化的能力。然而为了严谨地证明控制系统的稳定性,还需满足如下假设:

假设1:期望输出信号y*(k+1)是有界的,则存在1 个有界的u*(k),将此信号输入到系统中,使其输出等于y*(k+1)。

假设2:当任意时刻k及Δu(k)≠0时,伪偏导数的正负不会发生改变,即满足ϕ (k)＞ε ＞0,或ϕ(k)＜-ε。

在无人艇艏向控制系统中,由于其艏向输出范围为-180°～180°,当控制输入(舵角或偏航力矩)增大时,受控系统输出(艏向角)并不是一直增大,不满足CFDL-MFAC 方法对受控系统的“拟线性”假设2,导致该方法不能直接应用于艏向控制子系统中。

针对艏向控制子系统不满足上述假设2 的问题,廖煜雷等[13]针对艏向控制子系统的特殊动力学特性,引入重定义输出增益,提出了RMFAC 方法。其原理如图5 所示。

图5 RMFAC 原理图Fig.5 Principle of RMFAC method

引入重定义输出

如果选择合适的参数K1,当控制输入增大时,K1r持续增大,抵消艏向 ψ减小的问题,确保受控输出ψ+K1r也随之增大,从而满足了假设2 的要求[13]。

针对无人艇艏向控制子系统,对于式(9),选择参数满足K1=1min＞2π/(maxTs)时,伪偏导数ϕ(k)＞0 恒成立;同理,当 ΔTr(k)＜0,也存在合适的K1使得 ϕ(k)＞0恒成立,即假设2 得以满足。其中,max为单位时间内最大正向转艏角速度。

2.2 FRMFAC 方法设计

2.2.1 重定义输出增益对控制效果影响分析

基于无人艇水平面运动模型,利用重定义输出增益分别尝试不同的K1值进行仿真实验。实验分别设置了K1=0、10、20和30等4 种情况,期望艏向角 ψ0为90°,仿真结果如图6 所示。

图6 不同重定义输出增益仿真对比Fig.6 Simulation comparison of different redefined output gains

对比可知,随着K1值的增加,无人艇的艏向控制效果越来越好,最大超调量逐渐减小,但也由此导致上升时间越来越长。因此,为了提高控制系统的响应速度,可适当减小K1值;相反为了降低控制系统的响应速度,可适当增加K1值。考虑波浪干扰情况下无人艇运动情况,在顺浪或逆浪情况下,无人艇受到的外界波浪干扰力是不同的,因此控制系统的响应速度可以在航行过程中进行相应调整,以更好地适应波浪环境。

2.2.2 方法步骤

针对无人艇在波浪干扰情况下的运动问题,并基于上述RMFAC 方法中重定义输出增益系数K1的不同对控制效果的影响,设计了FRMFAC 方法。该方法的设计思路为: 根据不同波浪及遭遇角情况,在顺浪和逆浪时采用不同的控制参数对无人艇进行控制。无人艇运动过程中其艏向与波浪方向是不断变化的,因此,需要考虑遭遇角与控制参数之间的关系,即: 顺浪情况下,应加快无人艇响应速度,对偏差快速进行调整;逆浪情况下,应减慢无人艇响应速度,防止振荡发生。同时,在不同波浪干扰条件下的控制参数也需要随着波高的增高而改变,即: 波高较小时,无人艇自身扰动不大,可以适当降低响应速度;相反,波高较大时,无人艇受到的扰动增大,需要提高其响应速度,防止发生危险。该控制方法原理如图7 所示。

图7 FRMFAC 原理图Fig.7 Principle of FRMFAC method

该算法主要包含以下步骤。

1) 确定控制器的输入输出变量,设定相应的论域。控制器采用二维输入,系统的输入分别为波高H、波浪遭遇角 χ,输出值为K1。接下来进行模糊化,将模糊子集分别用NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)表示[28]。根据实际工况条件,设定H的论域为(0,0.2,0.4,0.6),其模糊子集表示为{ZO,PS,PM,PB}。遭遇角 χ的范围为(0,2π),由于无人艇在顺浪与逆浪航向时的遭遇角呈现镜像的特点,因此,其论域可定义为(0,π/6,π/3,π/2,2π/3,5π/6,π),于是遭遇角的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。输出参数K1的论域可根据实际经验与实验得出。

2) 确定各模糊变量的隶属度函数,将系统输入进行模糊化。文中采用三角形函数作为隶属函数[29]。

3) 根据设计思路对模糊规则进行设计。根据不同波浪情况,依据控制原理对模糊控制规则进行设计,如表1 所示。

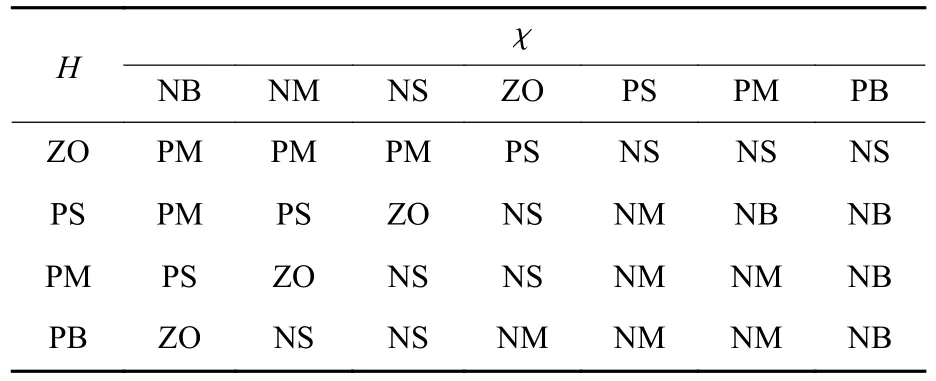
表1 K1模糊控制规则Table 1 K1 Fuzzy control rules

得到3 个控制参数的三维曲面图,如图8 所示。

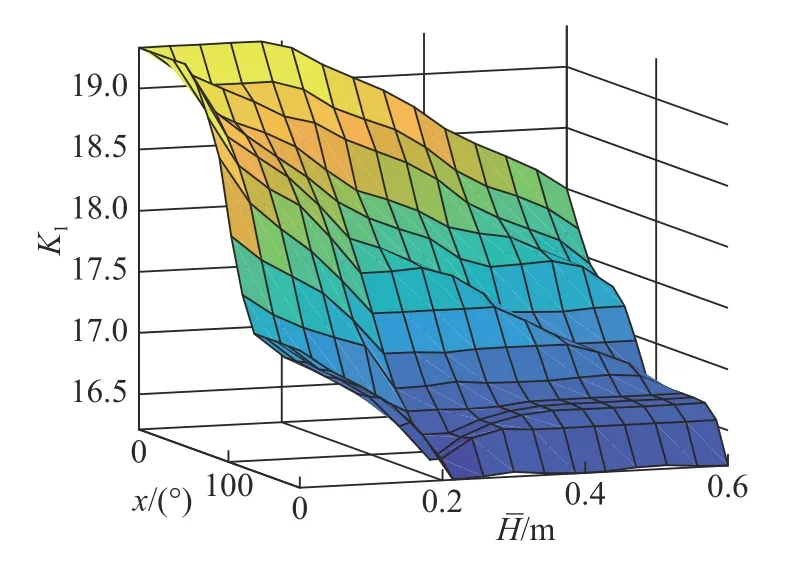
图8 K1三维曲面图Fig.8 Three-dimensional surface diagram of K1

4) 进行解模糊操作,最终得到输出值。得到模糊输出子集后,选用面积重心法进行去模糊化[30]。

2.3 基于视线法的路径跟踪方法

给定一条以参数化表示的路径曲线(Xd(θ),Yd(θ)),其中θ为与时间无关的曲线参数。

定义曲线的切向角

以跟踪点为原点建立S-F坐标系如图9 所示,对于在 (x,y)处的无人艇,其纵向跟踪误差xe和横向跟踪误差ye可以表示为

图9 无人艇路径跟踪示意图Fig.9 Schematic diagram of of path tracking

分别对xe和ye求导,通过联立可得

视线法制导律为

式中,Δ ＞0为无人艇的前视距离。

九曲蒋家208断裂总体倾角30°，2号主矿体与其产状基本相似，向深部愈加富集，局部倾角由陡变缓的地段往往是厚大矿体赋存位置，这也符合胶西北大型控矿断裂变缓控矿的规律[16-19]。

设计式(12)中up的表达式为

式中: κ为常量参数。

由式(15)与式(13)可得

3 仿真与分析

3.1 抗波浪干扰效果分析

通过对上文建立的无人艇运动数学模型进行的大量仿真实验,得到使用PID 控制方法时较优的控制参数为:kp=6,ki=0.01,kd=50;RMFAC方法较优的控制参数为: ρ=1,λ=0.1,η=0.8,µ=0.001,K1=20;FRMFAC 方法的参数为: ρ=1,λ=0.1,η=0.8,µ=0.001,其中K1由模糊规则根据实时波浪情况给出。

选取以X=100 m,Y=0 m为圆心,半径为100 m 的圆形路径,设定期望路径为

无人艇初始位置为(0,0)点,初始速度为0 m/s,初始艏向角为90°,设定前视距离 Δ=10 m。

分别在不同波浪干扰情况下,对PID、RMFAC和FRMFAC 等控制方法进行对比实验。仿真结果如图10 所示。

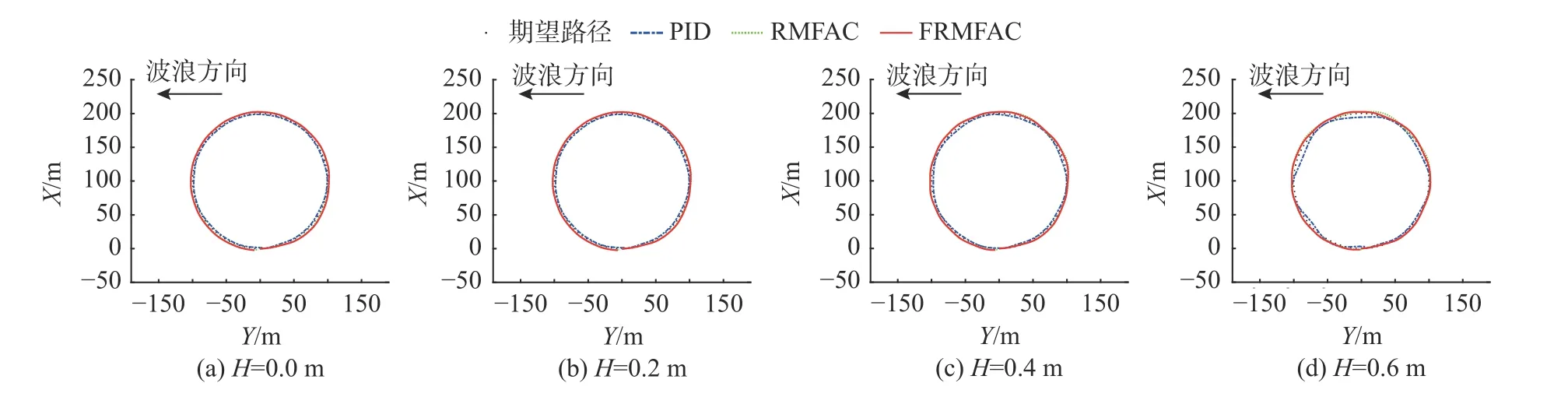
图10 不同波高下控制仿真结果Fig.10 Simulation results of different control methods at different wave heights

为了更好地对比仿真效果,采用均方根误差RRMSE对仿真误差进行计算(结果见表2),有

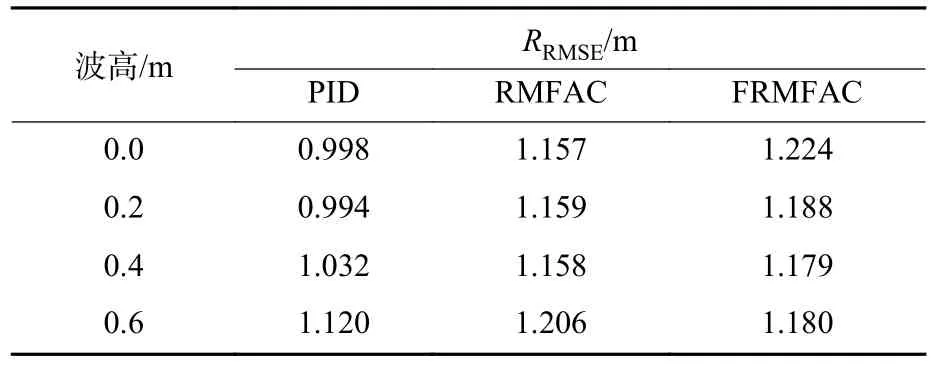
表2 不同控制方法的RMSETable 2 RMSE with different control methods

式中:d(ti)为每时刻无人艇的位置与圆心的距离;m为跟踪一周无人艇轨迹点的总数。

由表2 可以看出,3 种方法在不同波浪干扰情况下均可完成路径跟踪任务。但不同波高下的跟踪效果存在些许差异。随着波高的增加,3 种控制跟踪效果逐渐变差。在迎浪运动时,三者差别不大;但在顺浪运动时,PID 控制过大,导致一直处于跟踪路径内部,而RMFAC 和FRMFAC 在顺浪情况下随着波浪干扰力的增加,在误差允许的范围内逐渐远离跟踪路径,且两者之间的跟踪效果几乎重合。

3.2 节能效果分析

由于无人艇的推进方式为喷水推进,在恒定航速情况下推力基本一致,因此能量消耗差距主要体现在航向控制机构上。同时,舵机转动机构大范围频繁往复运动会造成机械结构磨损甚至降低使用寿命。图11 给出了使用PID 方法与FRMFAC方法在波高0.2 m 情况下舵机提供的转艏力矩变化情况。

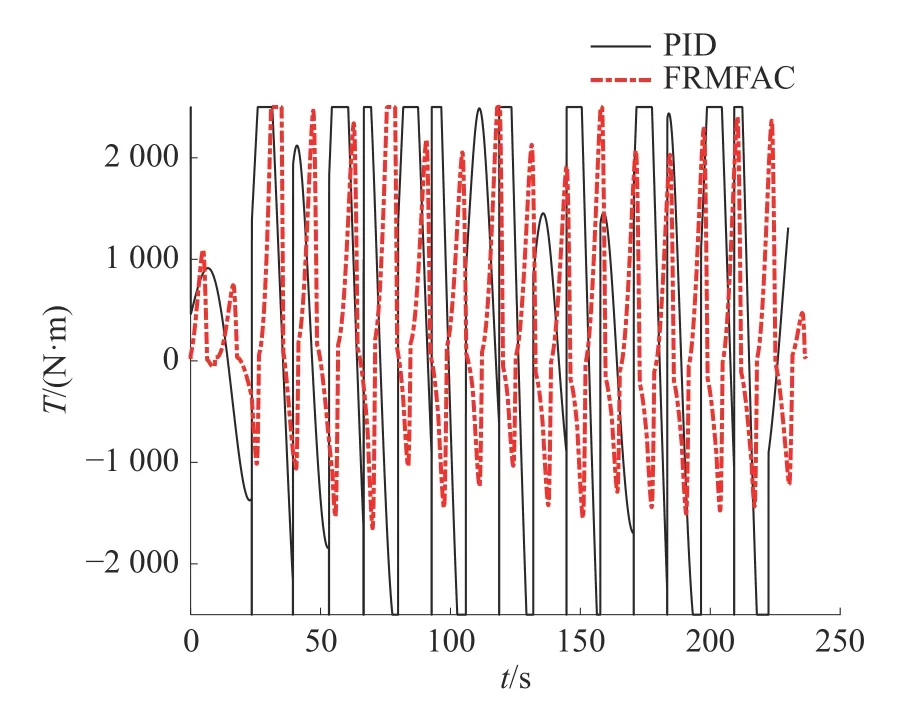
图11 H=0.2 m 时舵机提供的转艏力矩Fig.11 Bow turning moment provided by steering gear at H=0.2 m

由图11 可见,在使用PID 方法时舵机一直在最大转动范围内运动,相比之下使用FRMFAC方法仅有少数几次转动会触碰到最大舵角限制,其余时间均在正常工作范围内转动。因此,使用FRMFAC 方法可以有效降低舵角转动范围,进而提高舵机等操纵装置的使用寿命并起到节能效果。

通过对比3 种控制方法跟踪圆形轨迹一周舵机的能耗情况,对不同控制方法的节能效果进行分析。首先假设在恒定航速情况下该无人艇在不同舵角情况下对应的扭矩为线性关系,即T=Kδ,使用如下能量衡量方法对仿真结果进行量化[23]。

对上述圆形轨迹跟踪结果见表3。

表3 跟踪圆形轨迹一周舵机的能耗情况Table 3 Energy consumption of tracking circular trajectories one turn

从表中可看出,3 种控制方法控制艏向所消耗的能量均随着海洋环境干扰的增大而增加。在波高相同的情况下,FRMFAC 的能耗始终小于PID控制方法,与RMFAC 方法相比有部分提升。但在波高为0.4 m 时,FRMFAC 方法的节能效果达到了31.3%。在波高0.6 m 时,3 种控制方法的能量消耗均有所增加,FRMFAC 方法相较RMFAC 方法的节能效果最明显。可见在波浪干扰较大的情况下,相较其他2 种方法的效果提升十分明显,同时验证了使用模糊控制的方法更能节约能量。

对这种差异的原因进行分析。对于传统固定参数的PID 控制器和RMFAC 方法来说,为了应对多种复杂的海况环境,在设计时通常选取较大的控制参数,避免因控制响应速度不足,导致无人艇艏向控制失控。因此,在逆浪情况下,由于控制响应速度过大,造成舵机反复大范围转动,最终导致其能量消耗的增加。而对于FRMFAC 控制方法,其可在合理范围内对控制参数进行调节,在顺浪情况下,适当减小K1值,使无人艇快速响应;在逆浪时适当增大K1值,从而减少舵机反复转动角度范围,因此该控制方法可以达到节能的效果。