改进小波阈值降噪的汽车加速度信号处理
2024-03-13韦流权魏李帅贾亦雄易文彬彬
韦流权、魏李帅、贾亦雄、易文彬彬
(上汽通用五菱汽车股份有限公司 柳州 545007)
0 引言
随着汽车工业的迅速发展,汽车的性能评估变得越来越重要。其中,汽车的加速度信号是评估汽车动态性能的关键参数之一,它可以反映汽车的加速性、制动性以及行驶的平稳性等多方面的性能。因此,在汽车驾驶性评价中加速度信号所蕴含的信息很多,能否准确提取其信息并从中得到相应特征关系着驾驶性评价的准确程度。然而,在实际测量过程中,由于路面不平、传感器误差、电磁干扰等因素,采集到的汽车加速度信号往往含有大量噪声,这些噪声会严重影响信号处理的准确性和可靠性。
汽车加速度信号中噪声的特点较为鲜明,噪声信号与加速度信号相比,频谱广泛、频率成分更加复杂,且噪声信号多为高频信号。常用的低通滤波器、中值滤波或自适应滤波等可以通过信号的频率成分不同将噪声信号进行过滤处理得到可以反映加速度特征的去噪信号。但这些去噪方法将信号的高频成分直接过滤,不仅去除了噪声信号,也将加速度信号中本应含有的部分信息去除,得到的去噪信号反应汽车加速过程的加速度并不完整,尤其是当高频成分可能含有有用信号时。而傅里叶变换不具备时域分析能力,而窗口傅里叶变换在研究信号去噪时,窗口长度固定,在不同频率的信号下不具备普遍适应性。由于小波变换具有良好的表征时频局部特征的能力,能有效探测瞬变信号[1],因此工程上多应用小波变换对信号进行去噪处理。
目前,小波变换由于其在时频域内具有良好的局部特性,已经被广泛应用于信号的去噪处理中。通过选择合适的小波基和阈值方法,可以有效地移除加速度信号中的噪声成分,从而提高信号的质量。然而,尽管小波阈值降噪技术已取得了一定的成果,但仍存在一些问题和挑战。例如,如何选择最优的小波基和阈值方法以适应不同噪声环境下的信号处理,如何减少降噪过程中可能引入的信号畸变,以及如何提高计算效率等问题。此外,随着新型传感器和数据采集技术的发展,加速度信号的复杂性也在不断增加,这对小波阈值降噪技术提出了新的要求。因此,针对现有小波阈值降噪技术的不足,研究并提出改进的降噪方法,对于提升汽车加速度信号处理的精度和效率,具有重要的理论意义和应用价值。
1 小波阈值去噪
1.1 小波阈值去噪原理
小波阈值去噪由于其小波基选择的多样性,多分辨率分析的优良特性,以及阈值去噪的灵活性,在工程中应用较为广泛。含噪信号通过小波分解得到多个分量后,根据一个阈值选择合适的阈值函数进行量化处理,大于阈值的量保留,小于阈值的量去除,就去除了噪声。然后通过最底层低频分量和经过阈值处理的高频分量进行重构,得到的信号就是去噪信号。其基本步骤如图1所示。

图1 小波阈值去噪步骤
(1)小波分解:小波变换的原理是通过波形的尺度伸缩和平移来等运算功能对函数或信号进行多尺度细化分析。利用小波变换进行分解信号的灵活性在于,小波基函数的不唯一性。小波分解可根据信号的性质和特点来选择、推导或构建小波基函数。工程常用的小波基函数有Haar 小波、Daubechies小波(dbN小波)、coif 小波和sym小波等。利用这些小波基函数可对信号进行多分辨率分析,即把信号向嵌套的空间投影,Mallat 算法(多层分解,其分解层数根据信号特征确定),直到信号能清晰表达信号特征。分解层数一般根据经验确定或分解不同层数对比实际去噪效果选择。刘海江提出一种多指标融合的分解层数确定算法,但未得到广泛应用。
如图2 所示,通过Mallat 算法将信号分解成不同频率的分量,并将低频部分进一步分解。
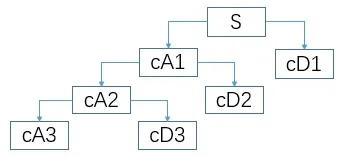
图2 小波分解过程
信号分解算法如下:
式中:S为含噪信号;cAi为第i层低频分量;cDi为第i层高频分量。
(2)阈值处理:阈值处理是去除噪声信号的关键步骤,含噪信号经过小波分解后,信号的小波系数会大于噪声的小波系数[2]。通过获取合适的阈值和阈值函数将低于阈值部分的信号置零,保留高于阈值的信号,便实现了噪声的去除。图2中,通过阈值函数进行置零处理可消除高频部分所含的噪声。
(3)小波重构:小波分解后信号的高频部分经过阈值处理去除了噪声,通过逆向小波变换进行重构即可得到去除噪声的信号。
小波去噪过程涉及小波基函数的选择、阈值获取、阈值函数选择、分解层数等多种参数,对各参数进行最佳设置,才能达到最好的滤波效果[3]。小波基函数的选择决定信号分解过程中信号的特征能否清晰表达出来,一般根据小波函数的对称性、正则性、消失矩等性质和信号的特征来确定。
本文对软、硬阈值函数进行改进,将软硬阈值函数进行折中处理,建立新的阈值函数,为去噪方法的优化提出思路。
1.2 小波阈值的获取
小波阈值的获取有如下多种算法。
(1)自适应阈值选择,使用Stein的无偏风险估计原理。对一个给定的阈值t,得到其似然估计,再将非似然估计t最小化,就得到所对应的阈值[4]。
(2)启发式阈值选择。
(3)极大极小原理选择阈值。
(4)固定阈值形式:固定阈值的大小由信号相关参数决定。
式中:λ为阈值;N为信号长度;σ为噪声的标准差。
阈值选取的方法较多,根据分析的信号特点选择合适的阈值方法能更好降噪。
2 阈值函数现状及改进
2.1 阈值函数现状
在利用小波阈值函数去噪时,传统的阈值函数主要包括硬阈值函数和软阈值函数[5]。硬阈值函数在均方误差意义上优于软阈值法,但是由于硬阈值函数的不连续,信号会产生附加震荡,产生跳跃点,不具有原始信号的平滑性。软阈值估计得到的小波系数整体连续性较好,从而使估计信号不会产生附加震荡,但是由于软阈值函数会使信号产生一定的偏差,直接影响到重构的信号与真实信号的逼近程度。
硬阈值函数为:
软阈值函数为:
式中:λ为阈值;j为分解层数;ω为小波系数;ωj,k为含噪信号小波变换后的小波系数。
硬阈值函数与软阈值函数各自存在一定缺点,硬阈值由于其自身不连续,信号会出现附加振荡;软阈值由于其偏差,这偏差会叠加至信号中。从阈值函数图可以看出硬阈值、软阈值与目标信号的差值(图3)。
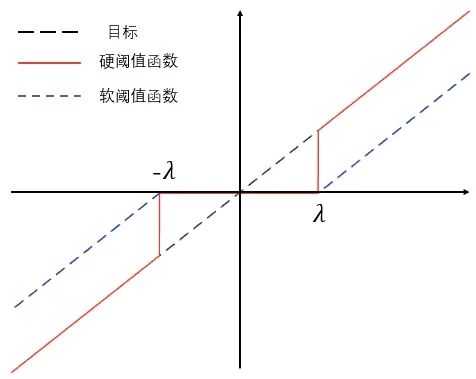
图3 目标及硬、软阈值函数图像
在许多文献中也提到关于阈值函数的改进,文献[6]将小波降噪与EMD结合使用,降噪效果更加明显。文献[7]提出了小波阈值函数族应满足的条件和一般构造方法。
2.2 阈值函数改进
根据硬阈值和软阈值函数的局限性,构造一种折中的阈值函数,该函数连续,且偏差较软阈值函数更小。其表达式如下:
式中:λ为阈值;j为分解层数;ω为小波系数;ωj,k为含噪信号小波变换后的小波系数。
改进阈值函数图像如图4 所示。
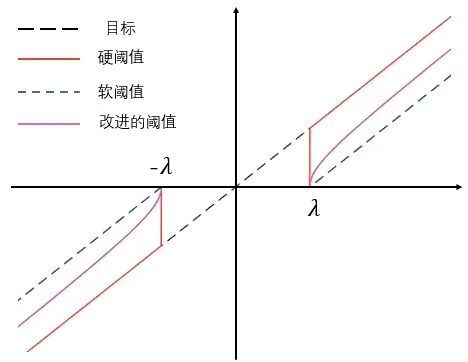
图4 改进阈值函数图像
3 汽车加速度信号处理
3.1 加速度信号采集
汽车加速度信号采集通过AVL-Drive 软件配套的DMU2数据采集仪,连接三轴加速度传感器进行测试(表1),并通过AVL-Drive导出。
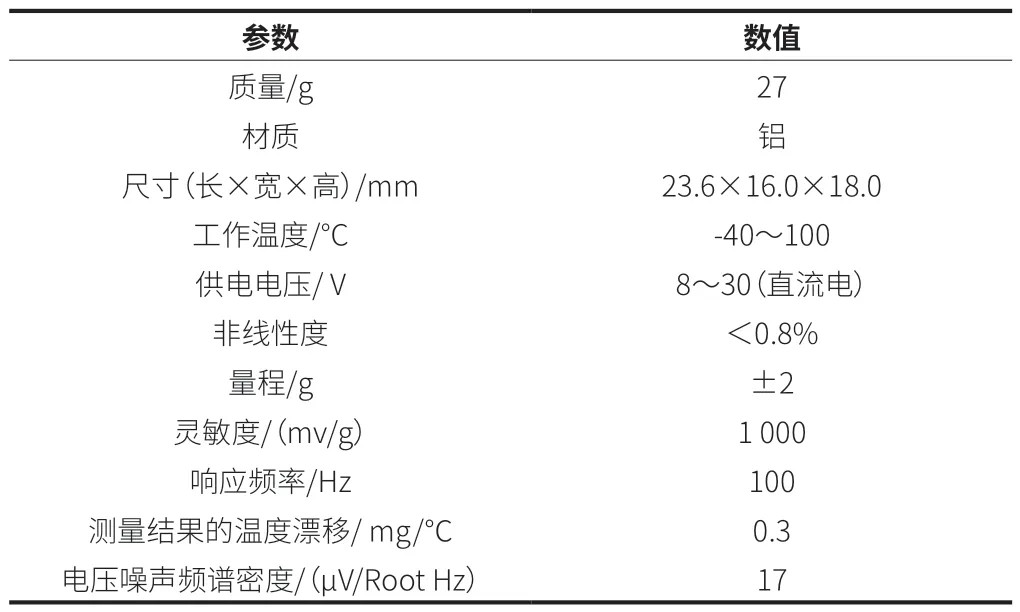
表1 三轴加速度传感器参数
加速度信号经传感器采集后,由于车载环境的影响,信号中包含较多噪声,若使用此信号直接进行驾驶性分析,可能会得出不准确的结论。因此需要对加速度信号进行降噪处理。
3.2 硬阈值、软阈值函数去噪
实际中广泛应用的小波阈值函数有硬阈值和软阈值,两种阈值方法均可对含噪信号进行去噪。两种阈值方法其对此含噪声信号的去噪效果如图5所示。
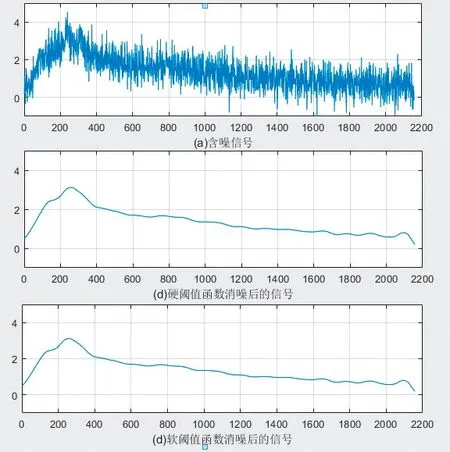
图5 硬、软阈值函数去噪效果
在MATLAB中对加速度信号进行处理,分析信号的特点,选择db6小波基,小波分解层数为5层,各层阈值分别获取。按照分解的各个尺度上用启发式小波阈值(heursure)方法对小波系数进行处理,然后用各尺度上的估计小波系数重构原始信号。
3.3 改进阈值函数的信号去噪
本文根据硬阈值和软阈值存在的不足,提出改进的阈值函数,该阈值函数介于硬阈值与软阈值之间,且函数连续,不会产生跳跃。其与目标值间虽存在一定偏差,但偏差较软阈值函数更小。选择db6小波基,小波分解层数为5层,各层阈值分别使用heursure获取,与前文各参数除阈值函数外,保持一致,对信号进行去噪处理,其结果如图6所示。
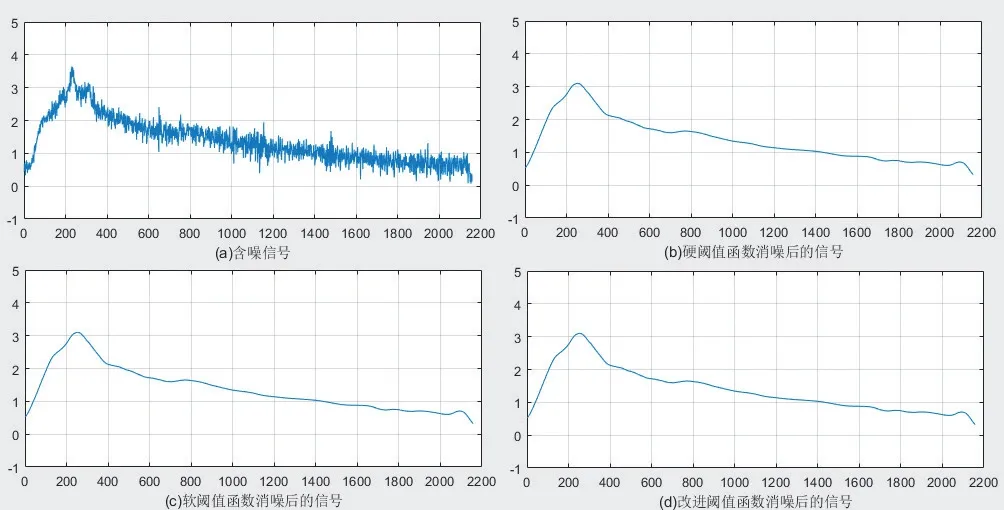
图6 不同阈值函数去噪
图6分别为含噪信号、硬阈值去噪信号、软阈值去噪信号和改进阈值去噪信号,可以看出各信号的去噪效果均较为优异,能很好地过滤掉噪声。各信号去噪后各方面参数如表2所示。

表2 各阈值函数去噪性能比较
由表2可知,使用改进的阈值函数去噪后,信号的信噪比值优于硬阈值函数和软阈值函数,均方误差值与硬阈值函数、软阈值函数的去噪方法差异不大。
4 结论与展望
相较于传统小波阈值降噪技术,本研究提出的改进方法能够更有效地去除汽车加速度信号中的噪声,同时保留了更多的有用信号成分,显著提高了信号的信噪比。根据硬阈值、软阈值函数的局限性构建折中的改进阈值函数,函数图像介于硬阈值和软阈值之间,其应用于小波分解降噪时,其信噪比大于硬阈值和软阈值函数,降噪效果更好;且均方误差与两者差异很小,性能较好。改进的阈值函数可以为小波降噪的阈值规则提供指导方向,同时为提高汽车加速度信号处理的准确性和效率提供了新的技术手段。
