基于IAGA的多行设施布局优化方法

曾强，陈永锋，袁瑞甫，赵水晶

(1.河南理工大学工商管理学院能源经济研究中心，河南焦作 454000；2.河南理工大学能源科学与工程学院，河南焦作 454000)

0 前言

设施布局是指在给定的空间与约束条件下，将生产所需的设施进行合理组合和安排，以便经济高效地为企业的生产运作活动服务[1]。现有研究表明，合理的设施布局可以有效降低10%～30%物料搬运成本、加快物料处理效率、减少在制品数量、缩短产品生产周期[2-3]。因此，开展制造业设施布局优化研究具有重要意义。

多行设施布局具有节约生产空间、物料传输柔性高、搬运设备利用率高等优点[4]，因此引起了国内外学者的广泛关注和研究。多行设施布局中分布有横向通道和纵向通道(统称为通道)，设施间的物料流动均沿通道运行。目前针对通道数量、位置均不确定及设施纵横比可柔性变化情况的研究较少。董舒豪等[5-6]先后针对纵向通道数量已知但位置不确定和纵向通道数量及位置均不确定的两个问题进行了研究，但均是基于设施长宽固定和横向通道位置及数量已知的前提。李玉兰、李波[7]构建了带有搬运设备空载成本的优化模型，但设施间物料搬运距离采用曼哈顿距离，并没有考虑物流通道，使得布局方案有可能无法满足实际需求。此外，通道数量和位置不仅直接影响设施间的物料搬运距离，而且对布局面积有一定影响。通道数量过少会增加设施间的物料搬运距离，通道数量过多则会直接增加占地面积成本，因此在布局过程中需要综合考虑通道的数量和位置。

多行设施布局是一个NP-hard问题，故启发式算法是求解该类问题的常用方法[8]。目前已在多行设施布局问题中应用的启发式算法有遗传算法[7，9-10]、粒子群优化算法[11-12]、蛙跳算法[13]、模拟退火算法[14]、珊瑚礁算法[15]等。其中，遗传算法是一类可用于复杂系统优化计算的鲁棒搜索算法。在遗传算法中，编码方式、交叉算子、变异算子在很大程度上决定了种群的遗传进化方向及遗传进化的效率，因此这三者的设计至关重要[16]。CHENG等[9]结合切片结构编码方式采用遗传算法对设施布局问题进行仿真实验，证明了遗传算法能够有效解决该类问题。HASDA等[10]对传统的遗传算法进行改进，提出交换算子和旋转算子，降低了搜索空间，提高了算法性能。李玉兰、李波[7]采用单亲遗传方式和单点交换的交叉算子对小规模设施布局问题进行求解，指出了单点交换的交叉算子搜索性能更好。因此，编码方式、交叉算子、变异算子的设计是遗传算法能否有效求解设施布局类问题的关键。

综合考虑多行设施布局过程中通道数量、位置均不确定及设施纵横比在满足最大纵横比约束的情况下对物料搬运成本和整体布局面积的影响，建立以物流成本、搬运设备空载成本及占地面积成本的加权平均值最小化为优化目标的布局优化模型，设计一种基于柔性隔间结构(Flexible Bay Structure，FBS)编码的改进自适应遗传算法(Improved Adaptive Genetic Algorithm，IAGA)，对该模型进行求解。

1 数学模型构建

1.1 问题描述

在有限的区域内分行布置n个设施，每相邻两行设施之间存在一条横向通道，中间行(除第一行和最后一行)中的每行至少存在一个纵向通道。假设如下：(1)所有设施均可看作规则的矩形；(2)所有设施面积和最大纵横比均为已知的固定值；(3)所有设施的物料搬运点均位于设施的中心点；(4)通道宽度为已知的固定值，且通道位置和数量可变；(5)设施布局方向已知。在以上假设条件下，为车间生产提供一个以物流成本、搬运设备空载成本及占地面积成本的加权平均值最小的设施布局方案。

1.2 变量定义

为方便描述布局优化模型，定义了如表1所示的变量。

表1 变量定义

1.3 优化模型

1.3.1 优化目标

以物流成本、搬运设备空载成本及占地面积成本的加权平均值最小化为优化目标，建立的目标函数如式(1)所示：

minc=w1×op1+w2×op2+w3×op3

(1)

(1)物流成本的量化

物流成本是指各个设施间的物流量、单位物流成本及搬运距离三者的乘积之和，按式(2)进行量化。

(2)

其中：设施间搬运距离采用文献[6]提出的3种方式(同行搬运、邻行搬运及跨行搬运)进行度量，如图1所示。

图1 三种搬运方式示意

假设从设施i搬运物料至设施j，则同行搬运距离和邻行搬运距离分别按式(3)和式(4)计算：

dij=|xi-xj|+|yi-y′i|+|yj-y′j|

(3)

d′ij=|xi-xj|+|yi-yj|

(4)

其中：y′i表示距离设施i最近的横向通道中心点的纵坐标。

跨行搬运可能存在多条路径如图1(c)所示，在搬运过程中需选择最短路径。采用邻接图对可行路径进行表示。以设施i、设施j及两设施所在行之间的纵向通道的中心点作为节点，邻行之间的节点是可达的，其权重为两节点间的距离，跨行节点为不可达，其权重为无穷大，记为∞。图1(c)的邻接图和可达矩阵如图2所示。采用floyd算法[17]求解最短路径。

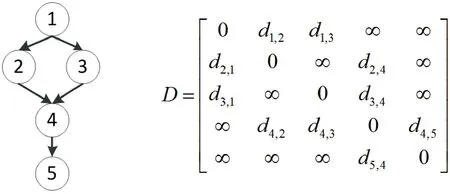
图2 跨行搬运方式的邻接图与可达矩阵

(2)搬运设备空载成本的量化

(5)

(6)

(7)

(3)占地面积成本的量化

设施布局占地面积是指当前布局下的最小包络矩形的面积，按式(8)进行量化：

op3=λ2×l′×w′

(8)

其中，l′和w′分别按式(9)和式(10)计算：

(9)

(10)

1.3.2 约束条件

模型的约束条件如式(11)—(17)所示：

(11)

(12)

(13)

(14)

s+v=1

(15)

s，v∈[0，1]

(16)

(17)

其中：i，j∈[1，2，…，n]；k∈[1，2，…，r]；ΔS为松弛变量。式(11)表示所有设施尺寸满足最大纵横比和面积约束；式(12)(13)表示所有设施均不超出规定的布置区域；式(14)—(16)表示任意设施间不发生干涉；式(17)表示第一行和最后一行不存在纵向通道，中间行至少存在一个纵向通道。

2 改进自适应遗传算法设计

2.1 IAGA算法流程

图3 IAGA算法流程

2.2 FBS编码及解码

柔性隔间结构(FBS)编码是由前、中、后三段构成，前段是长度为n的设施编号排列，中段是长度为n的隔间结构，后段是不定长度的纵向通道位置信息。根据布局编码信息从左到右、从上到下依次放置设施，解码过程如图4所示，其中纵向通道位置(3，0)和(4，1)分别表示在位置3前插入纵向通道和位置4后加入通道。每行设施的长(平行于x轴的边长)和宽(平行于y轴的边长)分别按照式(18)和式(19)计算：

(18)

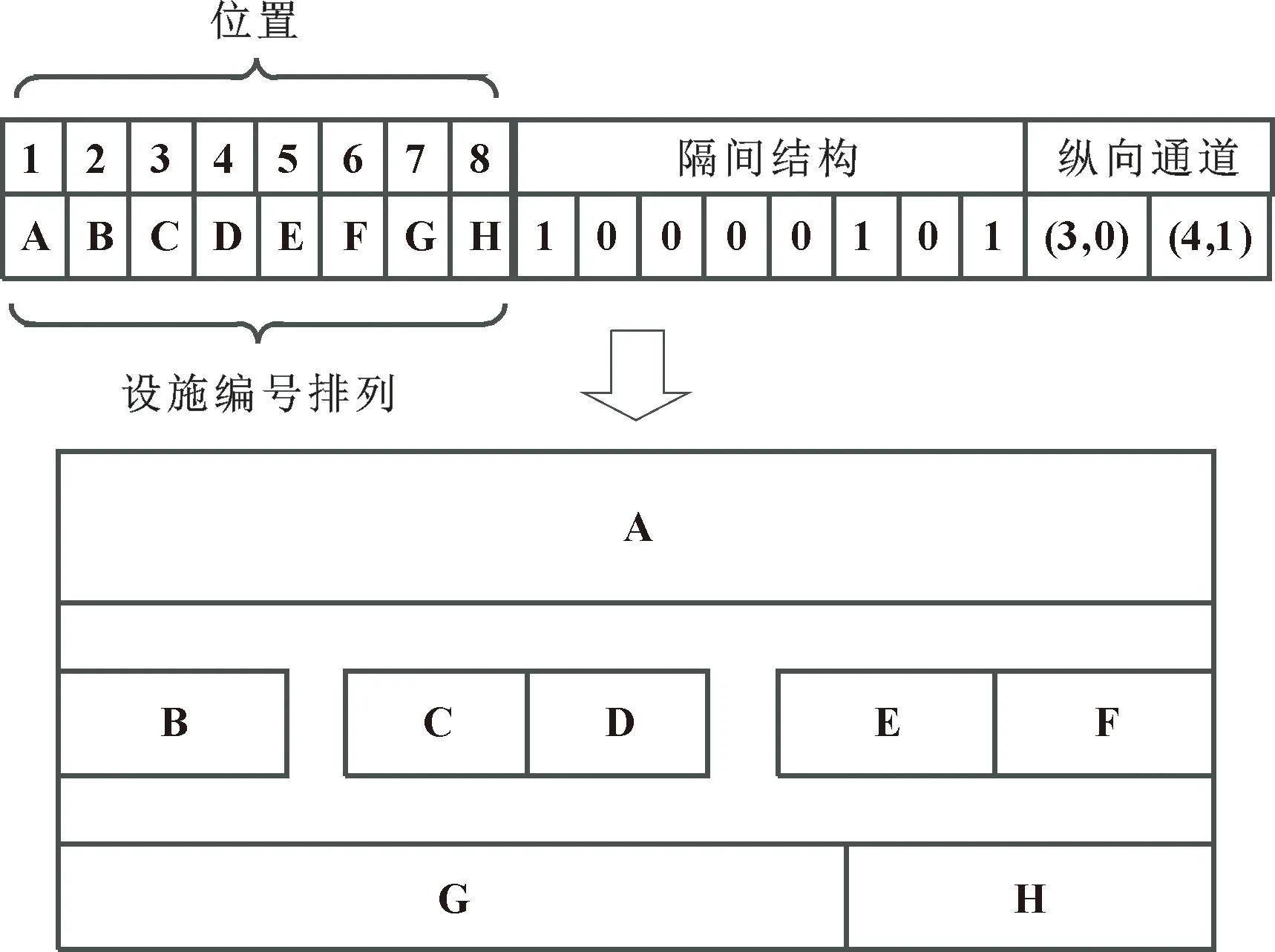
图4 布局编码及解码示意

(19)

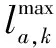
(20)

(21)

a1，a2，…，ank∈ψk

(22)

2.3 适应度函数

个体适应度按式(23)计算：

f(x)=1/(φ×op1+op2+op3)

(23)

其中：φ为惩罚系数，若当前解同时满足约束式(12)和约束式(13)，则φ=1，否则φ>1。

2.4 自适应交叉操作

基本遗传算法在种群进化过程中往往采用固定的交叉概率和单一的交叉算子。较高的交叉概率在种群进化前期能够快速筛除较差的个体，但在种群进化后期，个体适应度趋于平均值，全局的搜索需求降低，较高的交叉概率则容易破坏适应度较高的个体且单一的交叉算子难以兼顾全局搜索能力和局部搜索能力，导致在求解多峰值优化问题时易早熟。因此，采用自适应交叉概率方式[19-20]，动态调整交叉概率pc，适应度越高的个体发生交叉的概率越低，反之亦然。自适应交叉概率pc按式(24)取值：

pc=

(24)

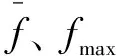
针对适应度较低的个体和适应度较高的个体分别设计了双点交叉算子和单亲单点交换算子。双点交叉算子可以对个体进行较大范围扰动，保证了种群进化过程中的个体多样性，提高算法全局搜索能力，如图5所示；单亲单点交换算子可以对个体进行小范围扰动，不易破坏个体结构，提高算法局部搜索能力，如图6所示。在种群进化过程中，以概率ps选择双点交叉算子，以1-ps概率选择单亲单点交叉算子。文中ps取值与pc相同。

图5 双点交叉示意

图6 单亲单点交换示意

2.5 变异操作

分别针对设施编号排列和FBS编码设计了两种变异策略，在种群进化过程中以等概率随机选择一种变异策略进行变异操作。

FBS编码变异：随机选择需变异个体FBS编码中的任意一个基因值进行取反操作(原值为0则置为1，原值为1则置为0)。

设施编号排列变异：随机选择需变异个体设施编号排列中的任意两个设施编号进行置换。

2.6 通道的更新

通道更新目的是确定当前个体的通道位置和数量。通道的更新步骤如下：

步骤1，依次为中间行的每一行随机生成一个纵向通道，并作为初始解x0。

步骤2，若不满足约束式(13)，且krow>1，则随机删除当前布局的一条横向通道，跳转到步骤1，否则执行下一步。

步骤3，若不满足约束式(13)，且krow≤1，则重新生成布局编码，跳转到步骤1，否则执行下一步。

步骤4，设置循环计数器初值t=1。

步骤5，随机选择中间行中的任意一行，以同等概率选择以下3种方式之一获得新解xnew。

方式一：为该行随机添加新的纵向通道。

方式三：随机选择当前行的一个纵向通道重新生成其位置。

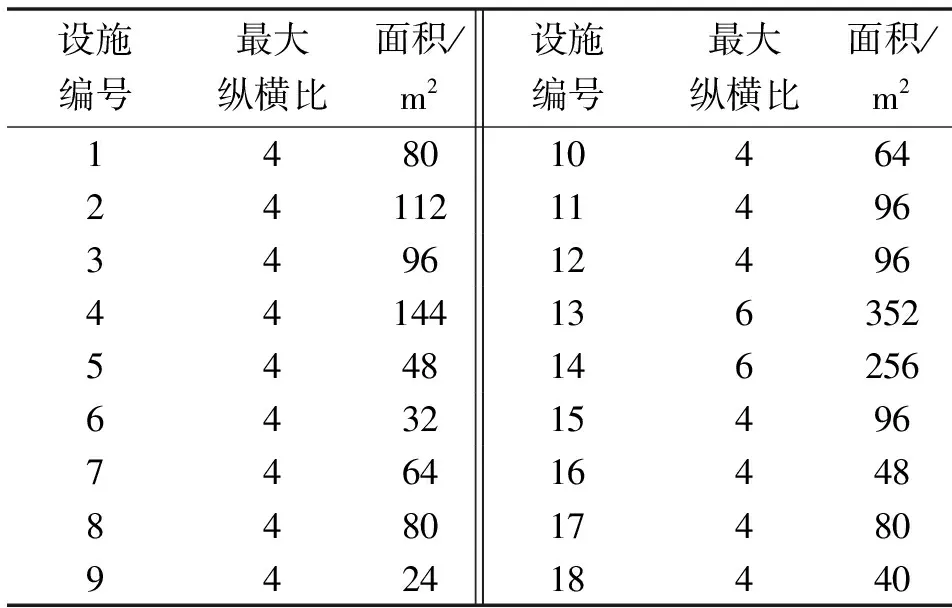
步骤6，若xnew不满足约束式(13)或f(xnew)

步骤7，若t

3 案例分析

将上述IAGA算法采用Java语言实现。为了验证文中所提方法的有效性，引用文献[6]中的案例进行分析。该案例中共有18个设施需要布置在长64 m、宽41 m的区域内，通道宽度为3 m。各个设施面积及最大纵横比如表2所示。所有设施间的单位距离搬运成本均取值为1元/(t·m)。设施间的物流量如表3所示，未列出的设施间物流量为0。

表2 设施面积和最大纵横比

表3 设施间物流量 单位：t Tab.3 Logistics volume between facilities Unit：t

式(1)中权重系数由专家打分法得出，分别为w1=0.5，w2=0.25，w3=0.25，取空载系数λ1=0.7、单位面积成本系数λ2=2。取种群大小m=80，进化代数ngen=1 000，交叉概率参数p′c=0.8、最大交叉概率pmax=1，最小交叉概率pmin=0.5，变异概率pm=0.1，惩罚系数φ=2。

在一台配置为Intel(R)Core(TM)i5-10210U CPU@1.60 GHz 2.11 GH及8.0 GB内存的计算机上独立运行IAGA算法20次，将所得到的最优解与原文献[6]中随机密钥蝙蝠算法(Random-Key Bat Algorithm，RKBA)独立运行20次的最优解进行比较，结果如表4所示。RKBA算法最优布局如图7所示，IAGA算法最优布局如图8所示。

图7 RKBA最优设施布局

图8 IAGA最优设施布局

表4 IAGA与RKBA运行结果

从表4可知：IAGA算法所得最优解优于RKBA算法，节约占地面积315.37 m2。表明IAGA算法能够有效求解带有最大纵横比约束的横向和纵向通道数量和位置均不确定的多行设施布局模型。

仅采用单亲单点交换算子的基本遗传算法(GAO)、仅采用双点交叉算子的基本遗传算法(GAT)及IAGA算法分别独立运行20次的对比结果如表5所示，3种算法对应的进化图和20次运行结果对比分别如图9和图10所示。

图9 三种算法的最优进化图

图10 三种算法独立运行20次结果对比

表5 三种算法运行20次结果对比 单位：元

从图9、图10和表5可知：GAO算法运行稳定性最差，表明该算法全局搜索能力较差，容易陷入局部最优；GAT算法收敛速度和求解质量最差，种群进化后期乏力，表明该算法局部搜索能力较差；IAGA算法运行结果最为稳定且最优解对应的总目标成本最低，收敛速度较快，搜索能力较强，表明该算法在求解文中所提的布局优化模型上表现出更好的性能。

4 结束语

针对横向和纵向通道位置和数量均不确定的多行设施布局问题，提出一种基于IAGA的多行设施布局优化方法。通过研究得出如下结论：

(1)构建的通道位置和数量均不确定的多行设施布局优化模型，考虑了设施最大纵横比约束，该模型以物流成本、搬运设备空载成本及占地面积成本的加权平均值最小化为优化目标，能较好地反映实际需求。

(2)设计的基于FBS编码的改进自适应遗传算法，能有效求解通道位置和数量均不确定的多行设施布局优化模型。算法中设计的FBS编码方式能够有效表示设施的位置信息，更容易生成适应度较高的个体。针对基本遗传算法对于多峰值问题求解时容易早熟现象，设计了自适应交叉概率、自适应选择双点交叉算子和单亲单点交换算子、针对隔间结构和设施编号排列的基本位变异算子，提高了算法性能。