上软下硬黏土中四筒基础抗倾覆承载特性研究

2024-03-12练继建黎慧珊

海洋工程 2024年1期

练继建，曹政，杨旭，2，黎慧珊

（1.天津大学水利工程智能建设与运维全国重点实验室，天津 300350；2.天津理工大学海洋能源与智能建设研究院，天津 300382）

风能作为最具发展潜力的三大清洁能源之一，资源丰富、可利用量大［1］。海上风电更是凭借平均风速高、风切变小、风机单机容量大［2］等优势逐渐成为各国风能开发的重中之重。近十年来，中国海上风电发展十分迅猛，每年新增装机容量不断增加（见图1）。中国在2021年“抢装潮”期间，新增装机容量呈现爆发式增长，远超其他国家。

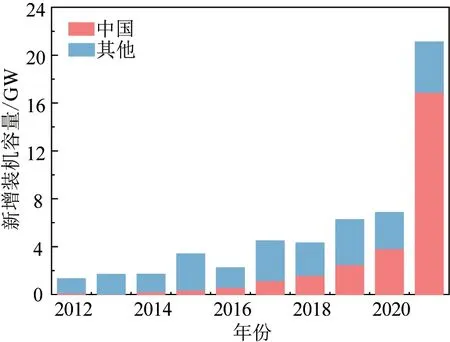
图1 全球新增装机容量[3]Fig.1 Latest global offshore installations

海洋环境十分复杂，风机机组在海上安全运行需要稳固的下部基础支撑。针对不同的地质和水文条件，各种基础形式［4］被相继提出。其中，筒型基础由于其具有施工操作简单［5-6］、造价低、承载性能好等特点而备受青睐。近年来，众多学者对单筒基础在单向荷载［7-11］以及复合荷载［12-13］作用下的承载力特性做了大量的研究。Barari和Ibsen［7］采用数值计算和物模试验的方法研究了不同长径比筒型基础在弯矩荷载作用下的极限承载能力，并简化了竖向—弯矩—水平复合加载屈服面表达式。Li 等［12］考虑扭矩荷载的作用，揭露了扭矩荷载对筒型基础承载力特性的影响。天津大学海上风电课题组通过在筒型基础内部增设分舱板，提出单筒多舱型筒型基础［14-20］，并提出基础—塔筒—风机机组一体化运输安装技术［21］。基于此基础形式，练继建等［22］研究了上覆软土层厚度和不排水抗剪强度对宽浅式筒型基础单向荷载承载能力的影响。

随着海上风电逐渐向深远海发展，上部结构向下传递的荷载逐渐增大，将多个单筒基础按照一定的形式进行排列并相互连接形成多筒基础，具有很大发展潜力。目前，多筒基础形式中研究较多的为三筒基础［23-27］和四筒基础［28-31］。Kim 等［25］针对三筒基础，提出承载组合效应因子的概念，揭示了承载组合效应因子与筒间距和筒高的相关性。Hung和Kim［26］研究了筒间距、筒高以及土体性质对三筒基础水平—弯矩承载能力的影响，并提出水平—弯矩承载力包络线与长径比相关的计算公式。丁红岩等［29］研究了砂土地基中不同上覆软土层厚度对宽浅式四筒基础在单向荷载作用下承载力特性的影响。乐从欢等［30］建立了不同长径比的四筒导管架基础，发现筒高对砂土中基础抗弯承载能力的影响更为显著。中国海上风电场主要建立在福建、广东、江苏等海域，海床以淤泥和软黏土为主，且上覆软弱覆盖层较厚，因此考虑黏土中上覆软土层厚度对基础承载力的影响十分必要。

针对上述问题，采用ABAQUS 有限元计算软件建立四筒基础模型，考虑不同筒间距、长径比和上覆软土层厚度的影响，研究了四筒基础在单向水平荷载、弯矩荷载作用下的承载力变化、筒壁土压力变化以及土体塑性区域分布规律，为四筒基础的合理性设计提供指导性建议。

1 计算方案

1.1 有限元模型

采用ABAQUS建立四筒基础有限元计算模型，图2为计算模型示意图。为了下文描述更加清晰，将单个筒按照顺时针顺序进行编号。每个单筒直径D=12 m，筒的厚度t=16 mm；四筒基础结构材料为钢材，弹性模量E=210 GPa，泊松比υ=0.3。为了降低地基边界效应的影响，土体有限元模型尺寸为200 m×200 m×100 m；土体模型底面限制6个方向的自由度，土体模型侧面约束径向位移。基础与土体之间切向采用摩擦接触，摩擦因数取值为0.35，法向采用硬接触形式。整体结构网格模型均采用C3D8R 单元，基础与土体接触区域网格进行局部加密，整体模型网格数量约为360 000 个。以黏土中大港滩海四筒基础模型试验［32］为例建立有限元模型，图3 给出了模型试验与有限元计算结果对比，可见2 种方法得到的结果变化趋势一致，偏差较小。

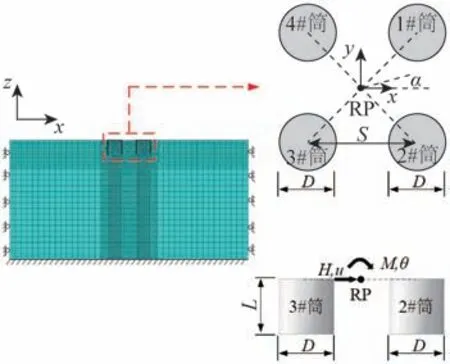
图2 计算模型Fig.2 The calculation model

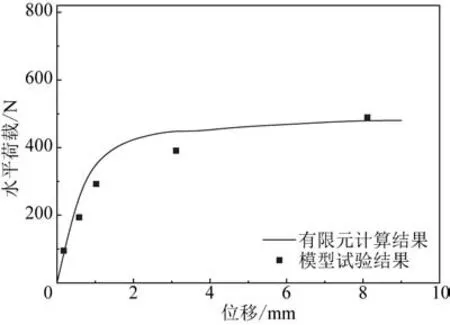
图3 四筒基础模型试验与有限元结果对比Fig.3 Comparative analysis of experimental and finite element results for the four-bucket foundation

1.2 确定加载方向

为明确加载方向对四筒基础承载力特性的影响，选取筒高L/筒径D=1，筒间距S/筒径D=1 作为计算模型。参考福建某风电场地质条件，土体设置为均质粉质黏土，弹性模量E=12 MPa，不排水抗剪强度Su=40 kPa。四筒基础之间通过与参考点（如图2中点RP）耦合进行刚性连接［25］，参考点位于四筒基础筒顶面几何中心处。采用位移控制法分别对参考点施加单向水平位移和转角，得到地基荷载—位移关系曲线。

荷载施加方向与x轴正向的夹角α分别设置为0°、15°、30°和45°，如图2所示，得到不同加载方向下的水平荷载—位移和弯矩—转角关系曲线，如图4所示。当荷载—位移曲线斜率接近0时，表明荷载并不随着位移的增大而持续增大，即认定四筒基础达到了极限平衡状态，对应的荷载即为四筒基础的极限承载力。由图4 可知，不同的荷载作用方向对四筒基础达到水平极限承载力和弯矩极限承载力所对应的位移和转角的影响并不显著。其中：水平极限承载能力随着夹角的增大而增大，如图4（a）所示，分别是95、97、99 和101 MN，与α=0°时比较，分别增加2.1%、4.2%和6.3%，说明在黏土中，水平荷载作用方向对四筒基础的水平极限承载能力影响较小；弯矩极限承载能力同样随着夹角的增大而增大，如图4（b）所示，分别是1 102、1 118、1 167 和1 223 MN·m，与α=0°时比较，分别增加1.5%、5.9%和11.0%，相较于水平极限承载能力，荷载作用方向对弯矩极限承载能力的影响更为显著。在黏土中，当夹角α为0°（即对边加载）时，四筒基础水平极限承载能力和弯矩极限承载能力均最小，为最不利工况。因此，这里仅研究荷载方向为0°时上覆软土层厚度和筒间距对四筒基础承载力特性的影响。

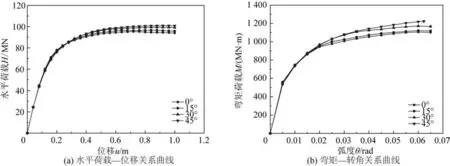
图4 荷载—位移关系曲线Fig.4 Load-displacement curves

1.3 计算组次

基于福建某海上风电场地质条件，上覆软土层主要是淤泥层，下层主要是粉质黏土层。土体分层示意如图5 所示，各分层土体参数取值如表1 所示。为了研究上覆软土层厚度对不同尺寸四筒基础在黏土中承载力特性的影响，软土层厚度h与筒高L的比值h/L分别取值为0、1/4、1/2、3/4、5/6 和23/24；四筒基础筒间距S与筒径D的比值S/D分别取值为1.5、2.0、2.5 和3.0；四筒基础筒高L与筒径D的比值L/D分别为0.7、0.9、1.0和1.5。

表1 土体参数Tab.1 Soil parameters

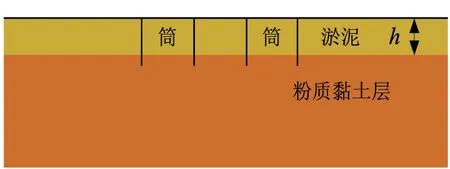
图5 分层土体示意Fig.5 Layered soil diagram

2 四筒基础水平承载特性

2.1 水平极限承载力

以L/D=1为例，在参考点上施加水平位移，得到不同筒间距下四筒基础水平极限承载力随着软土层厚度的变化趋势如图6（a）所示，L/D=1 时，水平极限承载力降低幅度在不同的筒间距下呈现出相同的变化趋势：当h/L≤3/4时，水平极限承载力降低幅度呈近似线性增加；当h/L＞3/4时，水平极限承载力降低速率明显减小。以S/D=2.0为例，得到不同长径比下四筒基础水平极限承载力随着软土层厚度的变化趋势如图6（b）所示，由图可知：当h/L≤3/4 时，四筒基础水平极限承载力降低幅度随着软土层厚度的增加近似线性增长；当h/L＞3/4时，水平极限承载力降低速率明显减小，且随着长径比的增加，承载力降低速率的减小趋势不断增大。

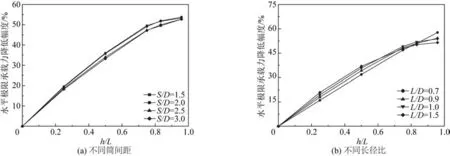
图6 软土层厚度对水平极限承载力影响Fig.6 Influence of soft soil thickness on horizontal bearing capacity

2.2 水平荷载下四筒基础运动模式

四筒基础在水平荷载的作用下产生平动和转动2种位移形式，将四筒基础视为刚体，运动位移包括平动位移（u，v）和转角θ，其中水平位移由整体水平运动和绕轴转动两部分叠加形成。仅考虑转动部分，四筒基础转动形式示意如图7所示。

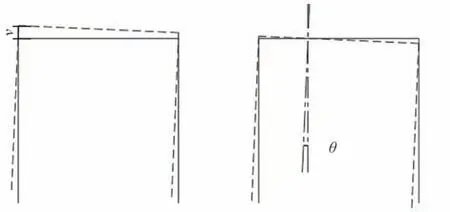
图7 四筒基础转动形式示意Fig.7 Four-bucket foundation rotation mode diagram

以L/D=1 为例，提取不同筒间距下的四筒基础在不同上覆软土层厚度达到水平极限承载力时的转角位移，如图8 所示。由8 图可知，随着筒间距和上覆软土层厚度的增加，四筒基础达到水平极限状态时产生的转动位移减小，四筒基础主要运动模式由转动变为水平运动。

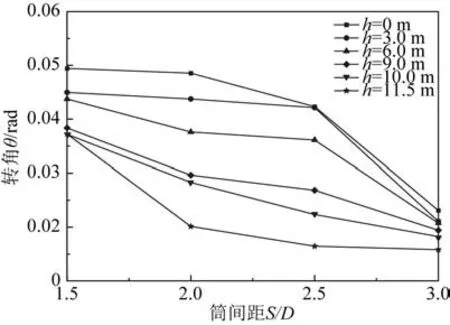
图8 水平极限承载状态下基础转角位移Fig.8 The rotation angle of the foundation in the horizontal limit bearing state

由于转角θ较小，忽略由于转动产生的筒顶盖水平位移，认为旋转轴水平位置近似与筒顶盖竖向位移为0 对应的水平位置相一致。以L/D=1.0，S/D=1.5、3.0 为例，沿1#筒与4#筒中心连线取不同上覆软土层厚度下筒顶盖竖向位移，得到中心连线各个位置竖向位移如图9所示。图9中1.5-3.0代表四筒基础筒间距S/筒径D为1.5，上覆软土层厚度为3.0 m时提取的筒顶盖中心连线各个位置竖向位移。由图9可知：四筒基础在水平荷载作用下产生转动，转动轴靠近受压筒1#筒且随着软土层厚度增加不断靠近四筒基础平面中心，但转动轴水平位置变化幅度较小。

图9 筒顶竖向位移Fig.9 The vertical displacement of bucket top cap

2.3 软土层厚度对土压力的影响

以L/D=1、S/D=2 为例，分别提取四筒基础达到水平极限承载力时筒壁位置a、b 不同埋深位置的水平位移和筒壁外侧土压力，得到不同上覆软土层厚度下四筒基础水平位移和土压力分布分别如图10 和图11 所示。由图10可知，对于筒壁位置a、b，土体被动区位于筒壁外侧土体，水平抗力主要由被动区土体提供。

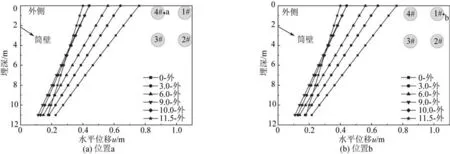
图10 不同深度筒体水平位移Fig.10 Horizontal displacement of the bucket foundation at varying depths

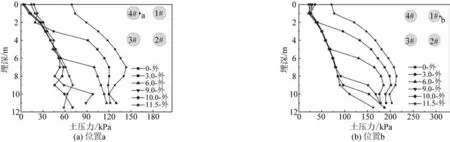
图11 不同深度被动土压力分布Fig.11 Passive earth pressure distribution at various depths

由于四筒基础在水平荷载作用下出现转动现象且受拉筒4#筒远离转动轴位置，基础转动影响较大，位置a外侧土压力分别在软硬土层内均呈现出先增大后减小的趋势（见图11（a））。受压筒1#筒靠近旋转轴，当软土层厚度不超过9.0 m 时，基础转动影响较大，位置b 外侧土压力呈现出先增大后减小的趋势（见图11（b））；当软土层厚度超过9.0 m 时，四筒基础达到水平极限承载力时的转角位移减小，基础转动影响减小，位置b外侧土压力随着埋深的增加不断增大。此外，土压力值在软硬土层分界面附近出现突增，且当软土层厚度超过9 m时，软硬土层内的土压力值存在相同的变化规律且不同软土层厚度下土压力值差别较小，因此当软土层厚度超过9.0 m时，四筒基础水平承载力降低速率减小。

2.4 水平荷载下土体破坏特征

以L/D=1.0，S/D=2.0，上覆软土层厚度h分别为6.0、9.0、10.0、11.5 m 计算方案为例，得到水平荷载作用下的土体等效塑性应变如图12所示。由图12可知：四筒基础在水平荷载的作用下产生转动位移，当上覆软土层厚度为6.0 m 时，筒外土体塑性破坏区域沿着筒壁分布在被动土压力区且在软硬土层分界面处不连续，筒内土体塑性破坏区域在软硬土层内均出现，说明软硬土层共同提供水平抗力；沿着荷载施加的方向，当软土层厚度超过9.0 m时，土体塑性区域分布形式类似，筒体前侧（即1#筒右侧）被动土压力区土体的塑性破坏区域沿筒壁分布在软硬土层内，筒体后侧（即4#筒左侧）被动土压力区土体的塑性破坏区域只出现在软土层范围内，筒体内部土体塑性区域主要出现在软土层，即当软土层区域进入塑性状态时，四筒基础达到承载力极限状态，说明当软土层厚度超过9.0 m时，四筒基础水平承载力主要由软土层性质决定。

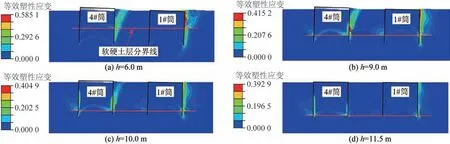
图12 水平荷载下土体等效塑性应变Fig.12 Equivalent plastic strain of soil under horizontal loading

3 四筒基础弯矩承载特性

3.1 弯矩极限承载力

取曲线斜率接近0 时对应的弯矩荷载作为四筒基础弯矩极限承载力，得到黏土地基中四筒基础弯矩荷载—位移关系曲线如图13所示。由图13可知：当筒间距和长径比一定时，四筒基础弯矩极限承载力随软土层厚度的不断增加均呈现出减小的趋势，且在不同的筒间距和长径比下具有相同的变化趋势。以S/D=2.0、L/D=1.0为例，当上覆软土层厚度分别为3.0、6.0、9.0、10.0、11.5 m时，四筒基础弯矩极限承载力相对于软土层厚度为0 m 时的降低幅度分别为16.20%、30.90%、46.09%、49.72%和54.04%，四筒基础弯矩极限承载力随着软土层厚度的增加近似线性降低，当软土层厚度超过9 m 时（即h/L＞3/4），承载力降低速率减小，但并没有水平承载力降低速率减小趋势那么明显。

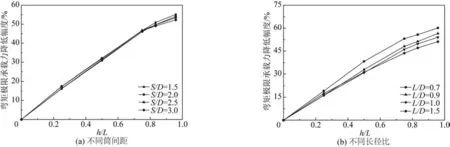
图13 软土层厚度对弯矩极限承载力影响Fig.13 Influence of soft soil thickness on bending moment bearing capacity

3.2 弯矩荷载下土体破坏特征

以S/D=1.5 和3.0，软土层厚度分别取0 和11.5 m 为例，在单向弯矩荷载作用下的土体位移如图14 所示。由图14可知：在弯矩荷载作用下，四筒基础转动轴位于受压筒1#筒内部且远离平面中心，随着软土层厚度的增大，转动中心越靠近1#筒左侧筒壁，但变化幅度较小；随着筒间距的增大，转动中心越远离1#筒左侧筒壁。当筒间距较小时，筒间土体受到两侧筒体的挤压作用而产生位移；当筒间距较大时，两侧筒体的挤压作用对筒间土体影响范围有限。

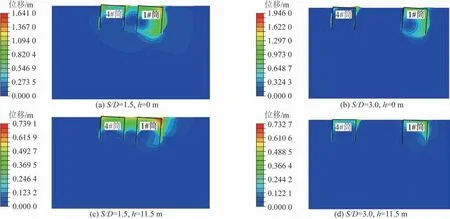
图14 土体位移Fig.14 Soil displacement

四筒基础达到弯矩极限承载力时的土体等效塑性应变如图15所示。由于在不同长径比和筒间距下，四筒基础弯矩极限承载力存在相同的变化特征，因此以S/D=2.0、L/D=1.0，软土层厚度h分别取6.0、9.0、10.0、11.5 m计算方案为例。由图15可知：当软土层厚度为6.0 m时，软硬土层中的土体塑性范围均分布在被动土压力区，受压筒1#筒在弯矩荷载作用下，竖向和水平方向挤压土体，筒体底部自筒端位置向下延伸形成连续的勺形破坏面；随着软土层厚度的增大，土体塑性破坏区域主要出现在软土层范围内，沿着筒壁自筒顶向下延伸，在软硬土层分界面并不连续，硬土层中土体塑性范围缩小，因此当软土层厚度超过9.0 m 时，弯矩极限承载力主要由软土层土体性质决定。

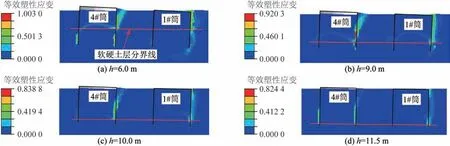
图15 弯矩荷载下土体等效塑性应变Fig.15 Equivalent plastic strain of soil under bending moment

3.3 软土层厚度对土压力的影响

以L/D=1.0、S/D=2.0为例，分别提取四筒基础达到弯矩极限承载力时筒壁位置a、b不同埋深的水平位移和筒壁内外土压力，得到不同上覆软土层厚度下四筒基础位置a、b筒侧水平位移和土压力分布如图16和图17 所示。由图16 可知：四筒基础在弯矩荷载作用下发生转动，受拉筒4#筒远离旋转轴，由于转动产生的水平位移较大，位置a和位置b被动土压力区域并未出现在筒壁同一侧，即上部分被动土压力区出现在筒壁外侧土体、下部分被动土压力区出现在筒壁内侧土体。

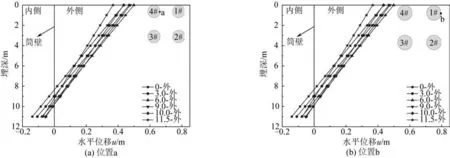
图16 不同深度筒体水平位移Fig.16 Horizontal displacement profile of the bucket foundation at various depths

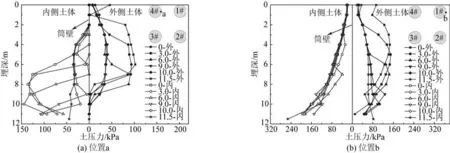
图17 不同深度筒壁内外侧土压力分布Fig.17 Earth pressure distribution inside and outside the bucket wall at various depths

土压力在软硬土层分界面位置出现突增，但当软土层厚度超过9.0 m 时，软硬土层范围内土压力大小和变化趋势基本一致（见图17），说明此时四筒基础弯矩极限承载力变化幅度减小。受压筒1#筒靠近旋转轴，转动影响较小，位置b 产生向下的竖向位移和水平位移，位置b 外侧土压力随着埋深的增加先增大后减小，内侧土压力随着埋深的增加而增加，当软土层厚度超过9.0 m 时，软硬土层内的土压力变化趋势一致且不同软土层厚度下土压力值差别较小。