火灾后高强钢管混凝土柱轴压的参数化分析

王晓初, 杨玉琪, 刘 晓, 回彦川, 崔洧瑄, 袁立灏, 朱 俊, 侯东序

(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)

高强钢管混凝土柱是在高强钢管(钢材屈服强度大于460 MPa)中填入高强混凝土(混凝土强度等级为C60及以上)形成的组合构件。对组合柱施加轴向压力时,钢管对混凝土起约束作用,延缓混凝土的纵向开裂,从而提高混凝土的抗压强度,同时由于混凝土的作用可延缓钢管出现局部屈曲。高强钢管混凝土柱在高层及超高层建筑中使用可以减轻结构自重,增强耐火性能,经历火灾后的高强钢管混凝土柱依然具有比较好的承载力。

目前,已有学者对高强钢管混凝土进行了研究:韩林海[1]通过研究矩形钢管混凝土柱在火灾后的力学性能和剩余承载力,确定了构件在高温作用后的应力-应变模型,同时简化了火灾后圆钢管和方钢管混凝土构件承载力的计算方法;刘晓等[2]利用有限元建立高强CFDST柱的计算模型,剖析了不同受火时间、外钢管屈服强度和混凝土抗压强度等因素对火灾后高强CFDST柱受轴压时的影响规律,结果表明外钢管屈服强度对火灾后高强CFDST柱的极限承载力影响较大;林晓康[3]利用ABAQUS建立火灾后普通钢管混凝土构件的数值模型,并对其载荷-变形关系曲线分析,深入了解构件在火灾后的受力特性;Xiong等[4]为了扩大设计规范应用范围,研究使用了高强和超高强材料的钢管混凝土在环境温度下的性能,对56组钢管混凝土短柱轴向性能进行试验,将试验结果与各国规范预测结果相对比,提出设计建议;Tao等[5]为评估火灾后结构的损伤,通过广泛收集文献测试数据,建立可用于加热和冷却后钢结构和钢筋的应力应变模型;王彦博等[6]对13组高强圆钢管混凝土短柱进行轴压试验,分析了钢管强度、混凝土强度及径厚比对构件轴压性能的影响,并将高强圆钢管混凝土短柱试验结果与现有试验数据对比,修正了其受压截面承载力计算公式;刘晓等[7]利用ABAQUS建立火灾后圆套圆CFDST柱模型,剖析了火灾后CFDST柱轴压工作机理并对其典型的承载力-位移曲线进行分析;刘晓等[8]考虑火灾受火时间、偏心距和空心率等因素,建立火灾后方截面CFDST柱数值模型,分析构件载荷-跨中挠度关系曲线,揭示方截面CFDST偏压工作机理;幸坤涛等[9]采用数值分析方法对高强钢管混凝土核心短柱受轴压时的载荷-变形关系曲线进行分析,简化了高强钢管混凝土核心柱轴压短柱承载力计算公式;王晓初等[10]使用ABAQUS有限元软件对高强方钢管混凝土短柱在高温后的轴压机制进行研究,发现构件在经历高温后各部件材料性能损失严重,构件极限承载力随所经历温度的升高而降低,构件承载力主要由高强钢材承担;王灿灿等[11]对6个圆形高强中空夹层钢管混凝土构件进行试验研究,利用ABAQUS分析了空心率、混凝土强度及内外钢管径厚比对该构件轴压性能的影响规律,并提出圆形高强中空夹层钢管混凝土构件轴压承载力和刚度的计算公式。

目前研究多集中在普通钢材、高强钢材在常温或高温条件下的力学性能,对在火灾后高强钢管混凝土的力学性能研究较少,本文利用ABAQUS有限元软件,创建火灾后高强钢管混凝土轴压模型,将有限元模型数据与文献试验数据对比验证,并对火灾后高强钢管混凝土进行参数化分析。

1 有限元模型

1.1 混凝土和钢材的本构模型

采用文献[3]提出的火灾后混凝土本构模型。火灾后高强钢材采用文献[1]提出的双折线模型,数学表达式为

式中:θ为钢材最高温度;fy为钢材屈服强度;fy(θ)为火灾后钢材屈服强度。

1.2 热工参数

本文选用文献[12]提出的热工参数:综合辐射系数即发射率取0.56;膜层散热系数取25 W·(m2·K)-1;混凝土容重ρc取2 400 kg·m-3;钢材容重ρs取7 850 kg·m-3。

1.3 建立模型

组合构件由钢管、核心混凝土和上下盖板3部分组成,组合构件边界条件如图1所示。

图1 组合结构边界条件

1) 建立温度场模型。钢管选用四结点传热四边形壳单元(DS4),核心混凝土和上下盖板采用八结点线性传热六面体单元(DC3D8);钢管与混凝土采用绑定(Tie)接触方式,可防止钢管与混凝土之间出现相对滑动或分离现象,也保障两者之间的热接触能力。

2) 建立力场模型。核心混凝土与盖板采用八结点线性六面体单元(C3D8R),钢管采用四结点曲面薄壳或厚壳单元(SR4);钢管内表面与核心混凝土之间、上下盖板与核心混凝土之间的接触类型均为表面与表面接触;钢管内表面与核心混凝土之间在切向上摩擦系数为0.6,法向上为硬摩擦;上下盖板与核心混凝土之间的切向行为和法向行为分别为无摩擦和硬摩擦。

各部件装配后,构件采用全局种子布种方式划分网格,网格划分精度为0.02,构件划分网格结果如图2所示。由于位移加载相较于力加载更加精确,本文选用位移加载,构件负载方式如图3所示,将柱底端盖板完全锚固,在柱底端X、Y、Z方向上限制柱底端的位移和转角,柱顶端施加位移载荷。

图2 构件网格划分

图3 构件负载方式

1.4 模型验证

为验证本文采用本构模型及建模方法是否合理准确,将文献[13]、文献[4]及文献[6]中试件承载力试验数据与本文有限元承载力模拟数据进行对比验证,试件模型参数见表1。

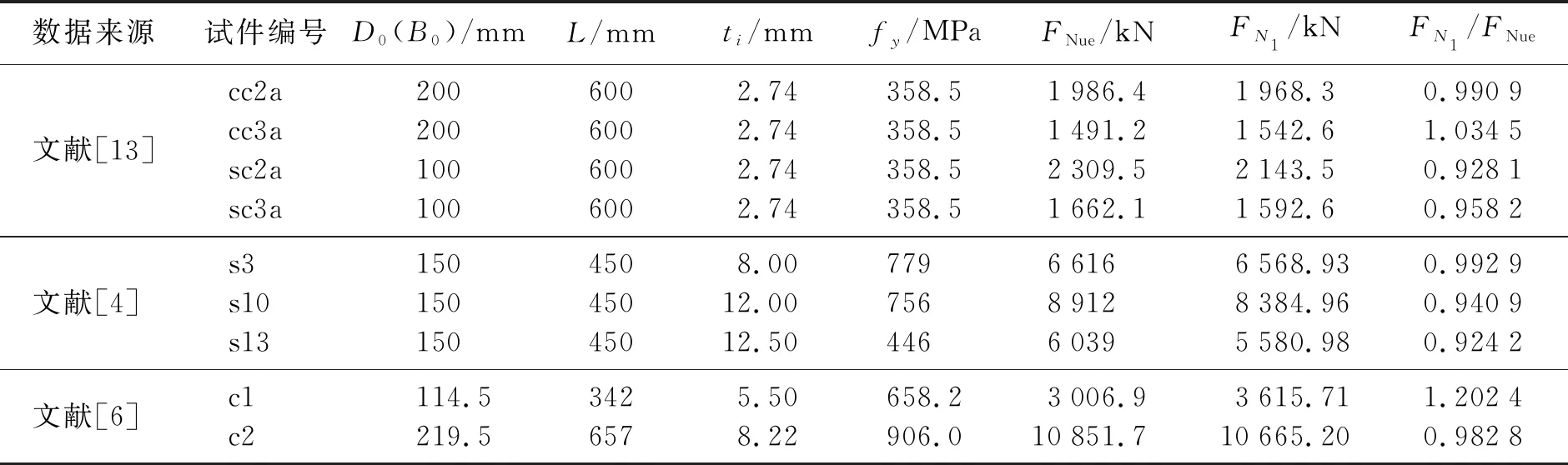
表1 各文献中试件具体参数

利用表1中数据计算可得承载力的有限元模拟值与承载力的试验值之比的平均值和标准差分别为0.995 0和0.080 6。 承载力(FN)-位移(Δ)曲线如图4、 图5和图6所示, 由图可见有限元模拟值曲线与文献试验值曲线趋势大致相同, 说明本文所采用的本构模型和建模方法是合理的。 因此可利用ABAQUS有限元软件对火灾后高强钢管混凝土柱受轴压时进行参数化分析。

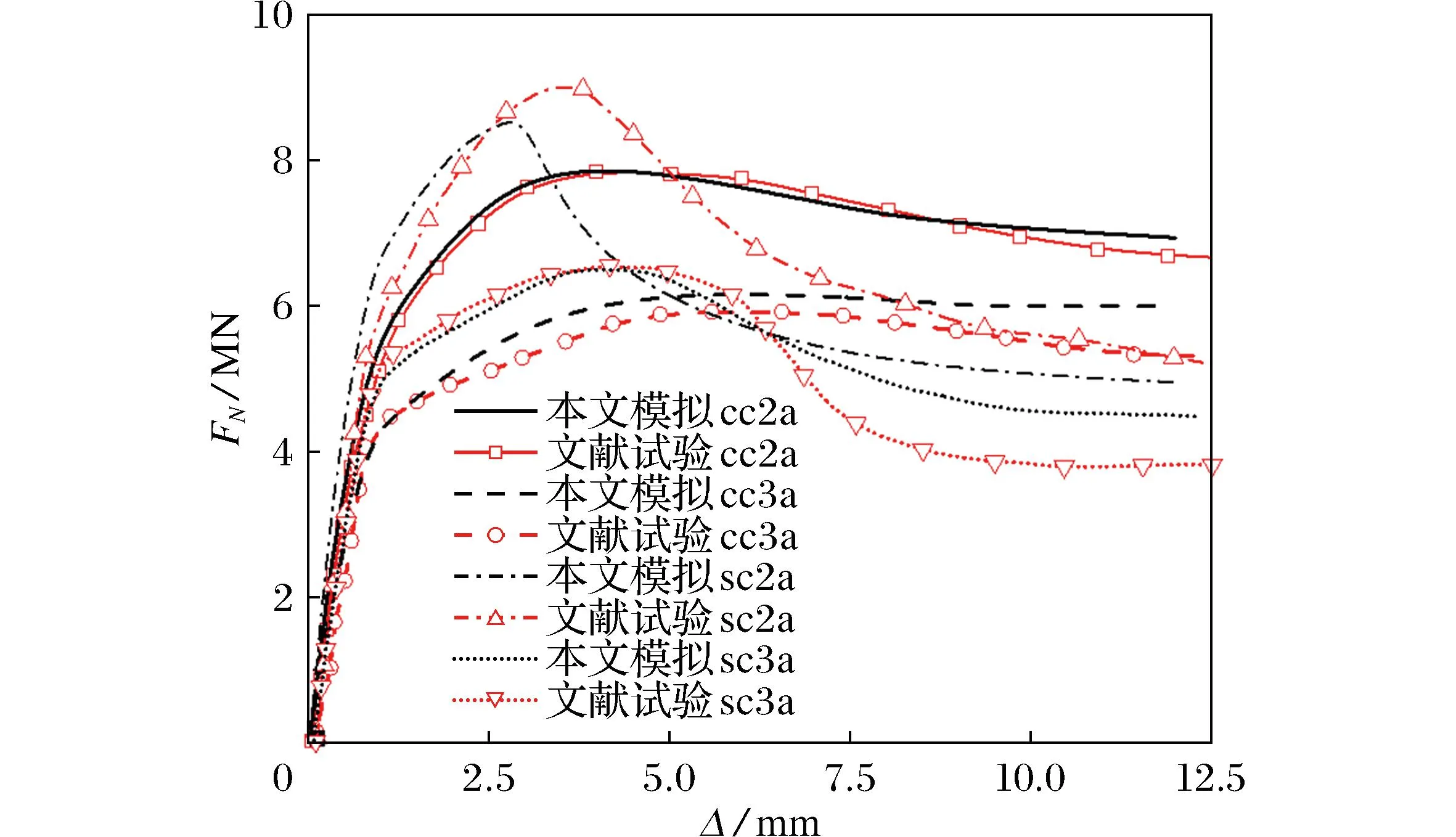
图4 本文与文献[13]的承载力位移曲线对比

图5 本文与文献[4]的承载力位移曲线对比

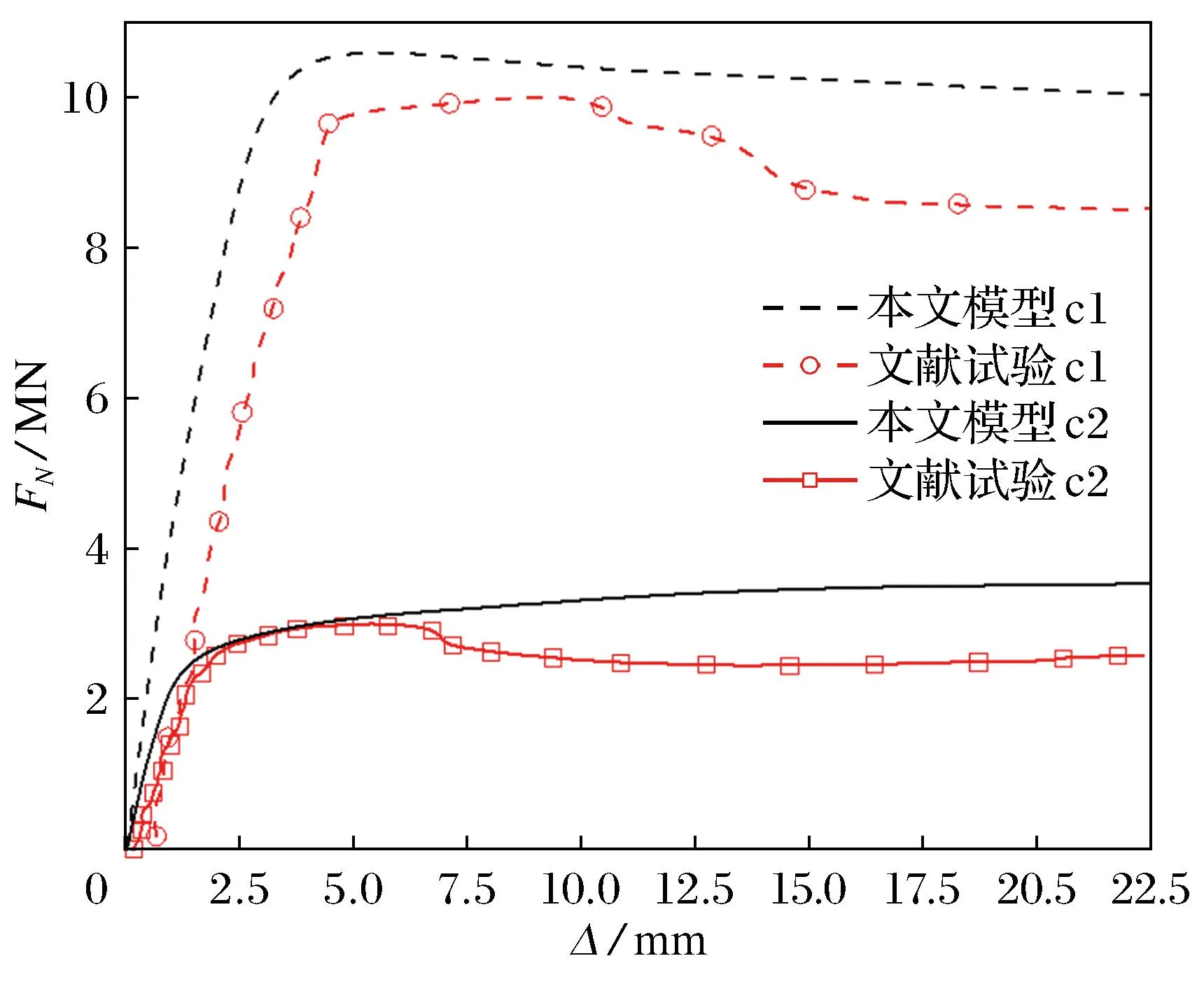
图6 本文与文献[6]的承载力位移曲线对比

2 有限元分析

有限元模拟中,选用圆截面高强钢管混凝土柱模型,模型上下端均采用300 mm×300 mm的方形盖板,构件中钢管长度均为600 mm,钢管直径均为200 mm,钢管壁厚均为3 mm。以受火时间t,钢材屈服强度fy,混凝土强度等级fcu为主要参数,建立10组高强钢管混凝土柱轴压模型构件,构件具体参数见表2。分析主要参数变化得出承载力-位移曲线以及对构件极限承载力产生的影响,同时与普通钢材进行对比。

表2 模拟构件参数

2.1 温度场分析

图7为构件在不同受火时间的核心混凝土温度场分布状况,取核心混凝土中截面1/4处作为研究对象。分析图7可知,核心混凝土在不同受火时间的内外温度差变化情况:随着受火时间增加,核心混凝土中截面1/4处的温度场以圆形波纹状从中间向外扩散,构件外边缘温度也逐渐增大;在受火时间60 min时混凝土的内部和表面存在较大温差,超过60 min后温差逐渐降低。

图7 不同受火时间构件中截面1/4处温度场分布

2.2 主要参数分析

2.2.1 钢管屈服强度

表2中的构件CC-10、CC-9、CC-6、CC-5、CC-4,受火时间均为90 min,对应钢材屈服强度分别为Q235、Q345、Q460、Q590、Q690,根据有限元模拟得到的数据绘制构件在轴向负载下不同钢管屈服强度的承载力-位移曲线如图8所示。分析图8可知构件的极限承载力逐渐提高:钢材屈服强度为Q690构件的极限承载力比钢材屈服强度为Q590构件的极限承载力提升了10.27%;钢材屈服强度为Q590构件的极限承载力比钢材屈服强度为Q460构件的极限承载力提升了16.75%;钢材屈服强度为Q460构件的极限承载力比钢材屈服强度为Q345构件的极限承载力提升了14.57%;钢材屈服强度为Q345构件的极限承载力比钢材屈服强度为Q235构件的极限承载力提升了19.45%。5组构件在达到极限承载力后均呈现下降趋势,从曲线下降幅度来看,钢材屈服强度为Q460、Q590、Q690构件的极限承载力的下降趋势比钢材屈服强度为Q235、Q345的更平缓。以CC-4构件的承载力-位移曲线为例,位移每增加2 mm选取一个点,取A、B、C、D、E五个点,B点承载力比A点增加253.11 kN,提升了15%;C点承载力比B点增加37.22 kN,提升了2%;D点承载力比C点减少22.56 kN,降低了1.1%;E点承载力比D点减少38.48 kN,降低了2%;构件承载力自C点以后下降3.7%,但降幅不大。因此,提升构件钢材屈服强度,极限承载力均增大,承载力在达到顶峰后,曲线下降平缓,说明使用高强钢材构件的极限承载力优于使用普通钢材,且构件在火灾后的延性较好。

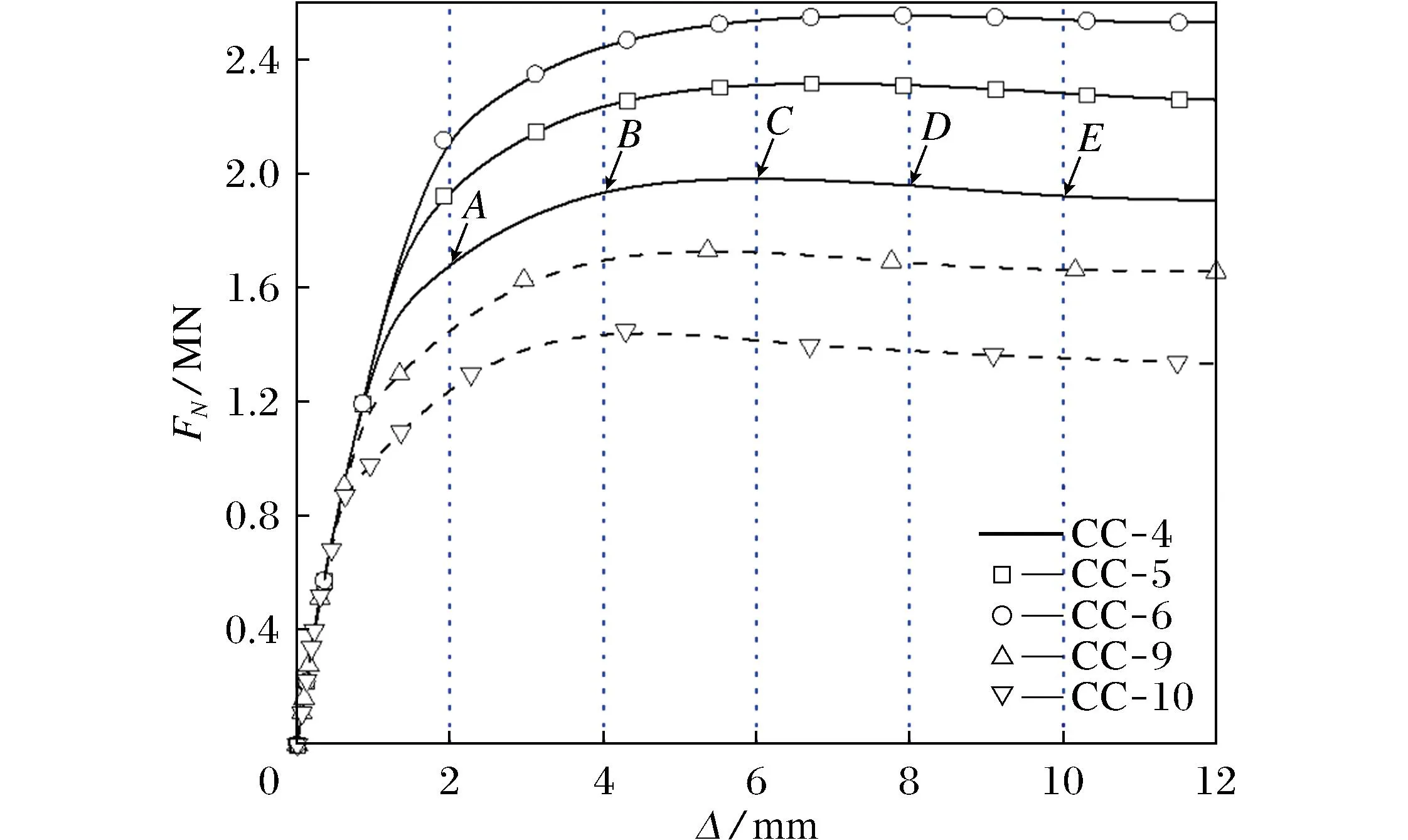
图8 不同钢材强度承载力位移曲线

2.2.2 受火时间

表2中的CC-1、CC-2、CC-3、CC-4构件的钢管强度和混凝土强度均相同,对应受火时间分别为30、60、90、120 min,根据有限元模拟得到的数据绘制构件经历不同受火时间后的承载力-位移曲线如图9所示。分析图9可知构件极限承载力逐步降低:受火时间从30 min到60 min时,构件极限承载力从2 716.62 kN下降到2 246.26 kN,下降了17.31%;受火时间从60 min到90 min时,构件极限承载力从2 246.26 kN下降到2 001.24 kN,下降了10.91%;受火时间从90 min到120 min时,构件极限承载力从2 001.24 kN下降到1 833.28 kN,下降了8.39%。以CC-3构件的承载力-位移曲线为例,位移每增加2 mm选取一点,取A、B、C、D、E五点,B点承载力比A点增加293.28 kN,提升了17.6%;C点承载力比B点增加45.49 kN,提升了2.3%;D点承载力比C点减少44.67 kN,降低了2.2%;E点承载力比D点减少21.83 kN,降低了1.1%;构件承载力上升至C点以后,承载力下降4.5%,自C点后曲线逐渐平缓。在构件均达到极限承载力后,受火时间30 min时,从B″至E″承载力下降了11.6%,受火时间60 min时,从B′至E′承载力下降了6.8%,曲线均出现明显下降;受火时间90 min时,构件承载力到达顶峰后曲线下降趋势变缓;受火时间120 min时,在达到构件极限承载力后,曲线无下降趋势。总的来说,随着受火时间增加,构件极限承载力呈明显下降到逐渐变缓趋势。这表明经历火灾后混凝土体积膨胀,产生很大的内应力,导致混凝土结构的破坏,水泥石产生较大收缩而骨料却膨胀,这种差异造成混凝土的破坏[14],此种破坏无法恢复,从而导致构件承载能力下降;而承载力无明显下降趋势则由于高强钢材在经历火灾,温度下降冷却后,钢材的材料性能可以大部分恢复,在火灾后构件展现出较好的延性。

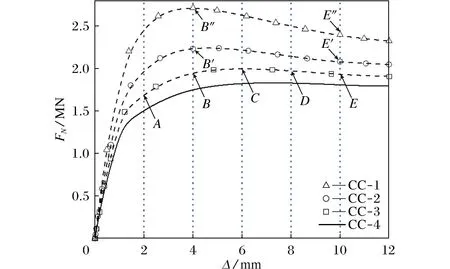
图9 不同受火时间的承载力位移曲线

2.2.3 混凝土强度

表2中的CC-8,CC-3,CC-7构件的受火时间和钢管强度均相同,对应混凝土强度分别为C60、C70、C80,根据有限元模拟得到的数据绘制构件在轴向负载下不同混凝土强度时的承载力-位移曲线(图10)。比较图10中的曲线可知:构件极限承载力提升较小,混凝土强度等级从C60提升至C70,构件极限承载力提升5.42%;混凝土强度等级从C70提升至C80,构件极限承载力提升6.75%。随混凝土强度等级的提升,构件极限承载力均略有提升,但在到达极限承载力后曲线渐渐下降。以CC-8构件的承载力-位移曲线为例,取A、B、C、D、E五点进行比较,B点承载力比A点增加249.92 kN,提升了14.9%;C点承载力比B点增加76.25 kN,提升了4%;D点承载力比C点减少67.92 kN,降低了3.4%;E点承载力比D点减少16.65 kN,降低了0.9%;随位移的增加构件承载力缓慢增加,在C点后构件承载力下降3.2%。由于混凝土是一种热惰性材料,传热较慢,根据温度场分析可知混凝土表层与内部存在较大温差,与传热快的材料相比,经历火灾后混凝土材料性能损伤程度较小,混凝土强度等级提升对构件承载力的提升较小。

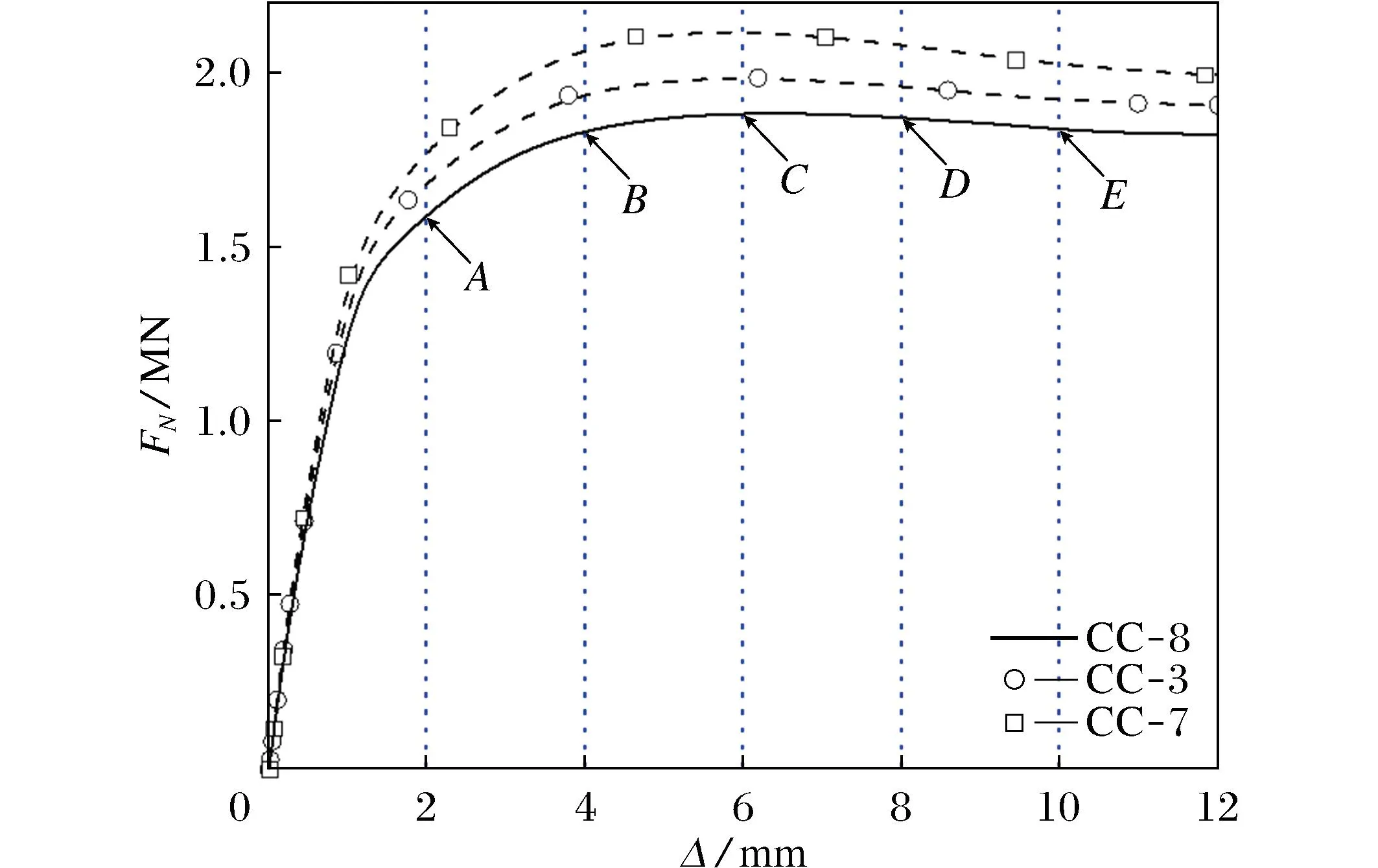
图10 不同混凝土强度的承载力位移曲线

3 典型曲线分析

图11为构件在受火时间为60、90、120 min的载荷-纵向应变曲线。分析图11可知:受火时间60 min时,钢管和核心混凝土分别占总承载力的29.61%和70.39%,受火时间90 min时,混凝土分别占总承载力的35.01%和64.99%,受火时间120 min时,钢管和核心混凝土分别占总承载力的37.46%和62.54%。随着受火时间增加,钢管所占总承载力的比例逐渐提升,混凝土所占总承载力的比例出现小幅度下降,但主要承担载荷的仍为混凝土。钢管和核心对火灾后高强钢管混凝土柱的轴压受力性能进行轴压工作机理分析,选取CC-8构件作为算例,其载荷-纵向应变曲线为图11(b)所示,O、A、B、C四点绘制对应的应力分布情况如图12所示。分析图11(b)与图12:O点对应构件施加轴力的起点、A点为弹性阶段结束点、B点为构件极限承载力点、C点对应构件纵向应变为0.02;OA段为弹性工作阶段,此时的OA段呈线性关系,由于混凝土的泊松比小于钢管,钢管与混凝土单独受力,混凝土未被压碎,钢管处于未变形状态但钢管两端出现些许应力集中现象;AB段为弹塑性阶段,随着轴力的增加混凝土加速膨胀,混凝土两端出现裂缝,钢管为混凝土提供约束作用;在B点以后,构件承载力开始下降,构件两端混凝土被压碎后逐渐退出工作,钢管对混凝土的约束降低,同时钢管中部开始出现应力集中。

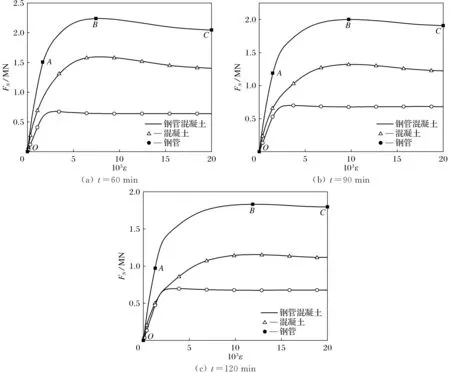
图11 典型载荷-纵向应变曲线

图12 O、A、B、C点应力分布

4 结 论

1) 随着钢材屈服强度的提高,构件极限承载力增大,高强钢材极限承载力明显大于普通钢材;随着受火时间的增加,构件承载力减小,构件在达到极限承载力后曲线变得逐渐平缓,说明使用高强钢材的构件在受火后展现出较好延性;增加混凝土强度等级对构件极限承载力提升较小。

2) 受火时间为60、90、120 min时,构件中的混凝土承担主要载荷。