实时参数整定的无模型自适应控制算法及其在气体分馏装置的应用

谷小峰，马庆鲁，黄文杰，李国庆

(1.华南理工大学化学与化工学院，广州 510640；2.山东京博石化公司)

随着流程工业,如炼油、化工、冶金、制药等行业生产工艺复杂程度不断增加,其传统的基于机理模型的控制方法(model-driven control,MDC)正面临越来越多的挑战[1-3]。随着信息技术的发展,工业过程数据收集和处理能力越来越强,这些数据包含了大量的工艺和设备信息,如何在难建立甚至无法建立机理模型的情况下,利用这些数据进行控制成为了控制研究的新课题。数据驱动控制(DDC)正是基于这种设想,通过挖掘蕴藏在数据中的信息而直接实现控制方案和控制器设计。近年来,DDC得到了迅速发展,出现了十余种方法[2,4-7],其中之一是无模型自适应控制(MFAC)[8-9],其基于伪偏导(PPD)概念将离散时间非线性系统转化成动态线性系统。伪偏导是一个时变参数,仅靠系统的输入/输出(I/O)数据估算,而无需建立被控对象的机理模型。同时借助于动态线性化方法,控制器的设计也相对简便。目前,MFAC已应用于自动泊车系统[10]、自动驾驶[11]、机械臂[12]、电机[13-14]、航天器姿态控制[15]和炼油化工过程[16-19]。

当前,MFAC研究主要从两方面展开:

(1)参数整定。MFAC有4个经验参数λ,ρ,η,μ,λ、μ为权重因子,ρ、η为步长因子。它们在控制方案设计过程中恒定不变,发明者未给出其整定方法,但它们深刻影响MFAC的跟踪性能。许多学者对参数整定进行了研究。郭代银[20]发现MFAC控制器与增量式比例-微分(PI)和比例-积分-微分(PID)控制器在结构上相似,可以用PID参数Z-N整定法和临界比例度法等来整定MFAC参数。胡益民等[16]提出了基于系统前3个时刻的初值,用拟牛顿法计算MFAC参数的方法,案例表明能改善MFAC的稳定性、不超调,但末期迭代次数较多。宋泽雨等[17]用遗传算法将四参数问题转化为单参数问题,在加速初期控制过程的同时也避免了可能出现的超调和震荡。但无一例外,上述方法都是离线整定,即通过系统初始参数整定得到的四参数在其后控制过程中一直保持不变,因而不能更好地适应时变过程,限制了伪偏导对控制过程的影响,自适应性不强。Yang Ye等[18]利用被控系统的输入输出实测数据用径向基函数(RBF)神经网络直接在线逼近每一时刻偏格式MFAC的伪梯度(PG);并利用长短期记忆(LSTM)神经网络,利用系统误差集和梯度信息集对控制方法的基本参数在线调优。最后,通过单输入单输出离散非线性系统仿真和三容水箱系统仿真验证了方法的有效性和适用性。

(2)优化MFAC跟踪控制。程志强等[21]针对执行器执行能力有限,即执行器饱和问题,提出了预报和滤波下一时刻输出,从而使预报值尽可能跟踪期望输出的方法。侯忠生等[10]提出了基于坐标补偿的MFAC算法,以消除自动泊车系统控制过程中实际泊车轨迹与目标轨迹存在的稳态误差,对下一时刻的输出期望进行修正,不过这一改进只是针对某一类对象,不具有普遍性。江浩斌等[22]结合滑模控制、模型预测控制改进了MFAC控制器,用理论分析证明了其稳定性,但算法参数多,十分复杂。

总体而言,MFAC在参数整定方面发表的研究多是离线整定,实时在线整定较少。在线整定根据系统当前I/O数据对每一时刻的四参数进行计算,因而能有效地提高控制过程的跟踪性能和自适应性能。本课题采用RBF神经网络对紧格式MFAC的四参数λ,ρ,η,μ进行在线整定,以建立一种新的RBF-MFAC方法,提高伪偏导对控制过程的影响,并将其应用于某非线性系统控制和某炼油厂0.3 Mt/a气体分馏(简称气分)装置丙烯塔的操作调整中。

1 无模型自适应控制

MFAC分为紧格式、偏格式和全格式3种。基于紧格式动态线性化的无模型自适应控制(CFDL-MFAC[23])的稳定性和收敛性有严格数学证明,本课题以其为研究对象。

考虑一类单输入单输出(SISO)离散时间非线性系统:

y(k+1)=f[y(k),…,y(k-n1),u(k),…,u(k-n2)]

(1)

式中:y(k)∈R,u(k)∈R分别为系统在k时刻的输出和输入;n1和n2是正整数;f(…):Rn1+n2+2R为未知非线性函数。可以证明,如果f(…)关于所有变量的偏导均连续,且系统满足广义Lipschitz条件,则有[23]:

Δy(k+1)=φc(k)Δu(k)

(2)

式中:Δy(k+1)=y(k+1)-y(k),Δu(k)=u(k)-u(k-1)分别为两个相邻时刻的输出和输入变化;时变参数φc(k)称为伪偏导。基于控制准则函数,可以证明[23]:

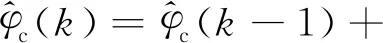
(3)

(4)

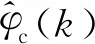
(5)

Δy(k+1)=Φc(k)Δu(k)

(6)

(7)

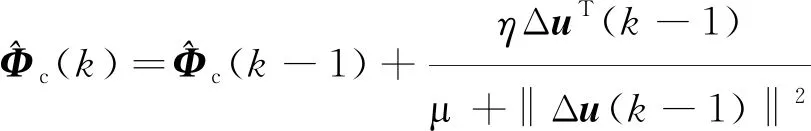
(8)

(9)

(10)

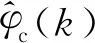
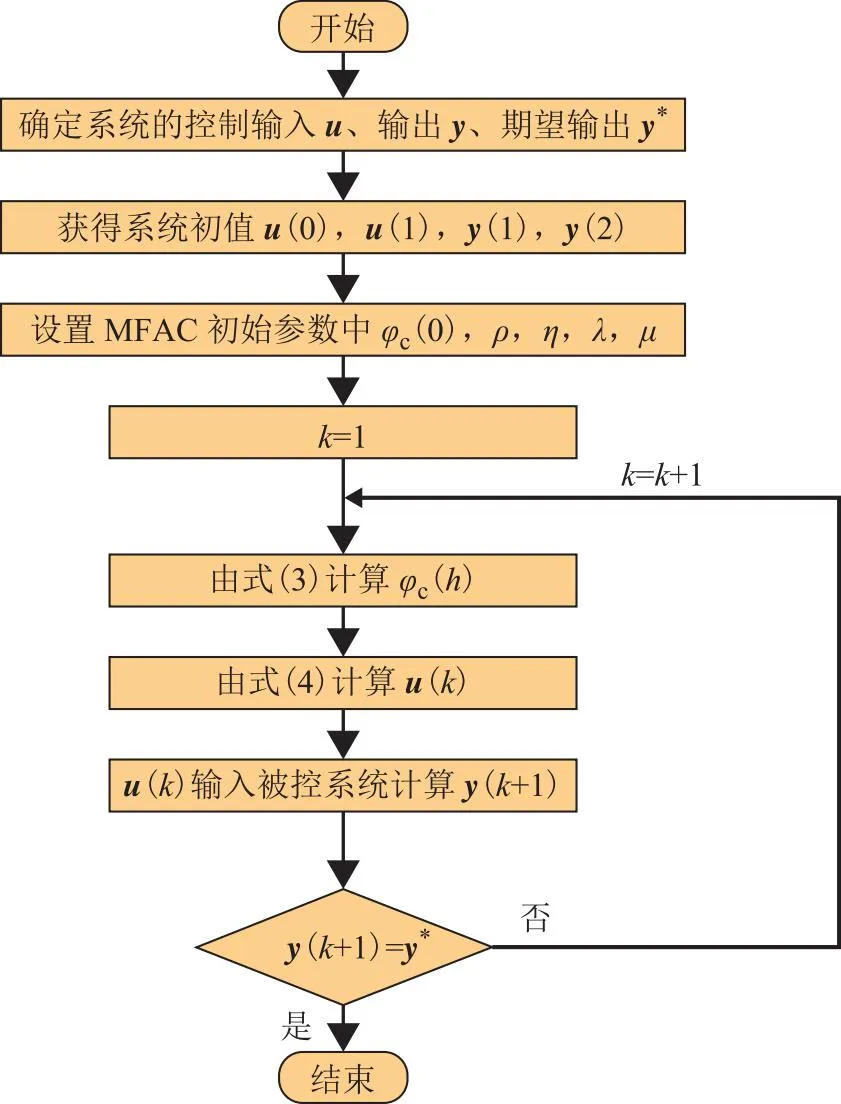
图1 SISO系统MFAC流程示意

MIMO系统的控制流程类似SISO系统,在此不赘述。

2 RBF神经网络整定MFAC四参数

2.1 RFB神经网络

RBF神经网络是由输入层、隐含层和输出层构成的三层前馈网络,是非常有效的非线性估计方法[24]。

RBF网络的输入可以表示为向量x,中心向量c与输入向量x维度相同,激活函数一般为高斯径向基函数(Gaussian radial basis function),隐含层的输出为:

(11)

式中:‖x-cj‖为两个向量间的欧氏距离;bj为基函数宽度,是正标量;m为隐含层神经元节点数。

RBF网络输出可以表示为:

(12)

式中:ω为输出层的权值;v为RBF神经网络输出;n为输出层节点数。

为了使RBF神经网络输出结果逼近系统期望输出,用于训练权值的误差为:

e(k)=vm(k)-v(k)

(13)

式中:vm(k)为系统期望输出;v(k)为系统实际输出。

取性能指标函数为:

(14)

利用误差反传播来更新RBF网络各层的权值系数。根据梯度下降法(GD),隐藏层至输出层的权值更新计算式为:

(15)

ωj(k)=ωj(k-1)+Δωj+α[ωj(k-1)-ωj(k-2)]

(16)

隐藏层基函数的系数bj和cij的更新计算式为:

(17)

bj(k)=bj(k-1)+Δbj+α[bj(k-1)-bj(k-2)]

(18)

(19)

cji(k)=cji(k-1)+Δcji+α[cji(k-1)-cji(k-2)]

(20)

式中:ξ∈[0,1]为学习率,ξ∈[0,1];α为动量因子,α∈[0,1]。

高斯径向基函数径向对称、两边递减,选取的中心向量接近输入向量时,对输入具有真实的映射作用,因此RBF神经网络具有学习速度快、不易陷入局部最优的特点[25],适用于解决MFAC的四参数实时整定问题。

2.2 MFAC四参数在线整定

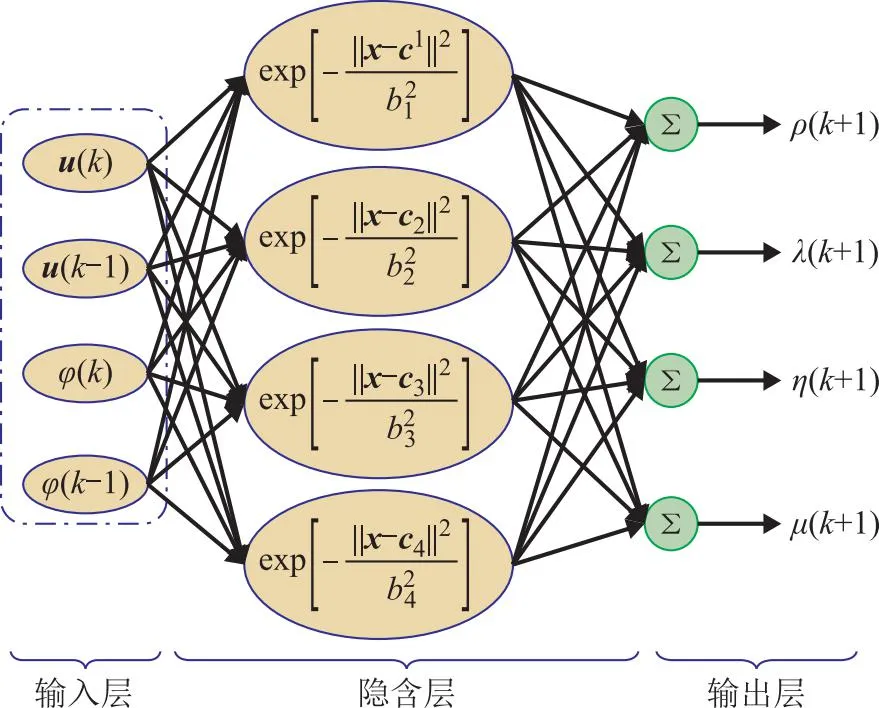
图2 基于RBF神经网络的参数在线整定示意

(21)

(22)

(23)

(24)

而后利用误差反传播来更新RBF网络各层的权值系数和中心向量[25]。由式(16)得到:

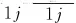
(25)

分别对ρ,μ,η求梯度,同理可得到ω2j(k+1),ω3j(k+1),ω4j(k+1)。

由式(18)得到:

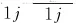
(26)

分别对ρ,μ,η求梯度,同理可得到b2j(k+1),b3j(k+1),b4j(k+1)。

由式(20)得到:

(27)

分别对ρ,μ,η求梯度,同理可得到其余基函数系数。

上述方法同样适用于MIMO系统,仅需将伪偏导数改为伪偏导矩阵,在此不赘述。

综上得到基于RBF神经网络实施四参数在线整定的MFAC算法(简称RBF-MFAC)框图,如图3所示。

图3 SISO系统RBF-MFAC示意

为了验证RBF-MFAC方法的优越性,将其应用于如下非线性系统[23]:

(28)

系统期望输出为:

(29)

图4为该非线性系统现有MFAC和RBF-MFAC控制跟踪性能,可见RBF-MFAC控制追踪性能优于MFAC。

3 案例应用

图5为某炼油厂0.30 Mt/a气体分馏(气分)装置的原则流程。由脱丙烷塔T101、脱乙烷塔T102和丙烯塔T103组成,工艺目标是分离来自催化裂化装置的液化气,得到摩尔分数99.6%的丙烯。由于丙烯、丙烷沸点接近(常压沸点分别为-47.7 ℃和-42.1 ℃),丙烯塔分离难度大,采用两塔串联,板数达200～240块,一旦原料组成波动,操作很难稳定[16]。研究目的是采用有效的控制策略,使丙烯产品纯度和产量尽快达标。

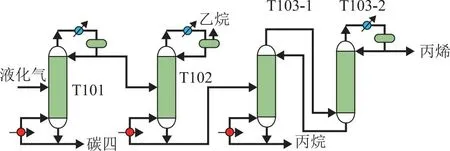
图5 某0.30 Mt/a气分装置原则流程

下面分SISO和MIMO两种情况进行讨论。

3.1 SISO系统

表1为丙烯塔进料和产品组成,产品中丙烯摩尔分数只有91.2%,未达到合格品要求。

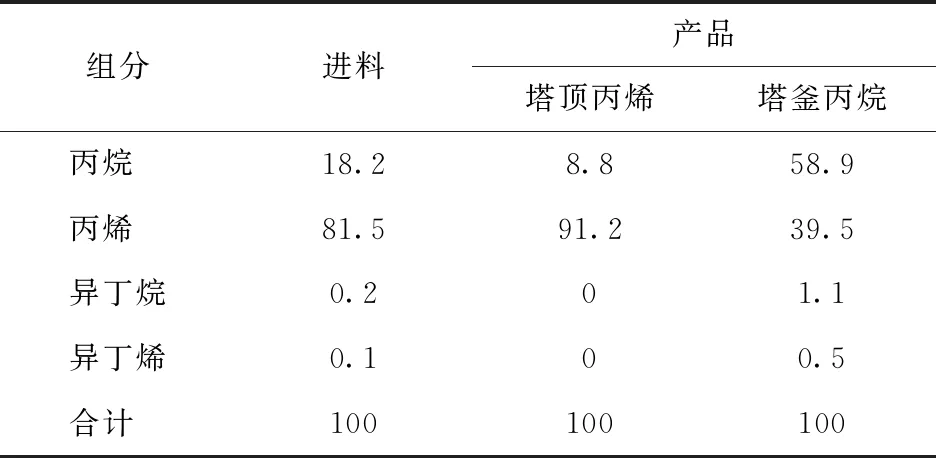
表1 丙烯塔SISO系统进料和产品组成 x,%

丙烯塔SISO系统操作参数见图6。保持丙烯塔塔顶压力1.79 MPa不变,丙烯塔自由度为1,故选择塔底再沸器负荷为输入u1,塔顶产品丙烯摩尔分数为输出y1,期望输出为yr1=99.6%。

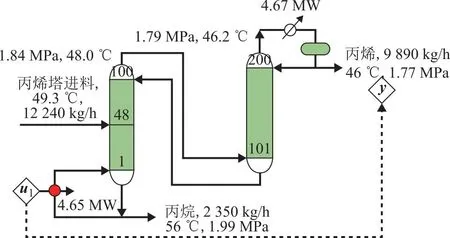
图6 丙烯塔SISO系统操作示意

Aspen Plus与Matlab数据交互平台,如图7所示。丙烯塔计算由大型商用流程模拟软件Aspen Plus V11完成,RBF-MFAC控制过程由Aspen Plus V11和Matlab 2022b交互平台实现。首先由Aspen Plus模拟取得k时刻I/O数据,然后由Matlab编写的MFAC或RBF-MFAC程序代码调用,未达到控制目标时,按图3流程整定得到k+1时刻四参数,计算得到的u(k+1)返回Aspen Plus模拟得到y(k+2),依次迭代,实现丙烯塔操作自动调整,达标后结束。

3.1.1MFAC方案

按图1流程得到丙烯塔SISO系统现有MFAC控制跟踪效果和伪偏导变化趋势,如图8所示,其中:y为塔顶丙烯摩尔分数;k为操作调整次数,可以理解为操作调整一次所需的单位时间。实际生产中塔的操作调整后,从当前的稳态生产转换到新操作参数下的新稳态时,需要一个过渡时间。由于本课题所提方法尚未应用到实际生产中,故该时间段长度未知。因此作了简化处理,近似认为每次调整操作后到新稳态的时间间隔相等。由图8可见:k=217时塔顶丙烯摩尔分数达到99.6%目标值;MFAC四参数保持不变时,伪偏导值变化缓慢,达到控制目标过程缓慢。

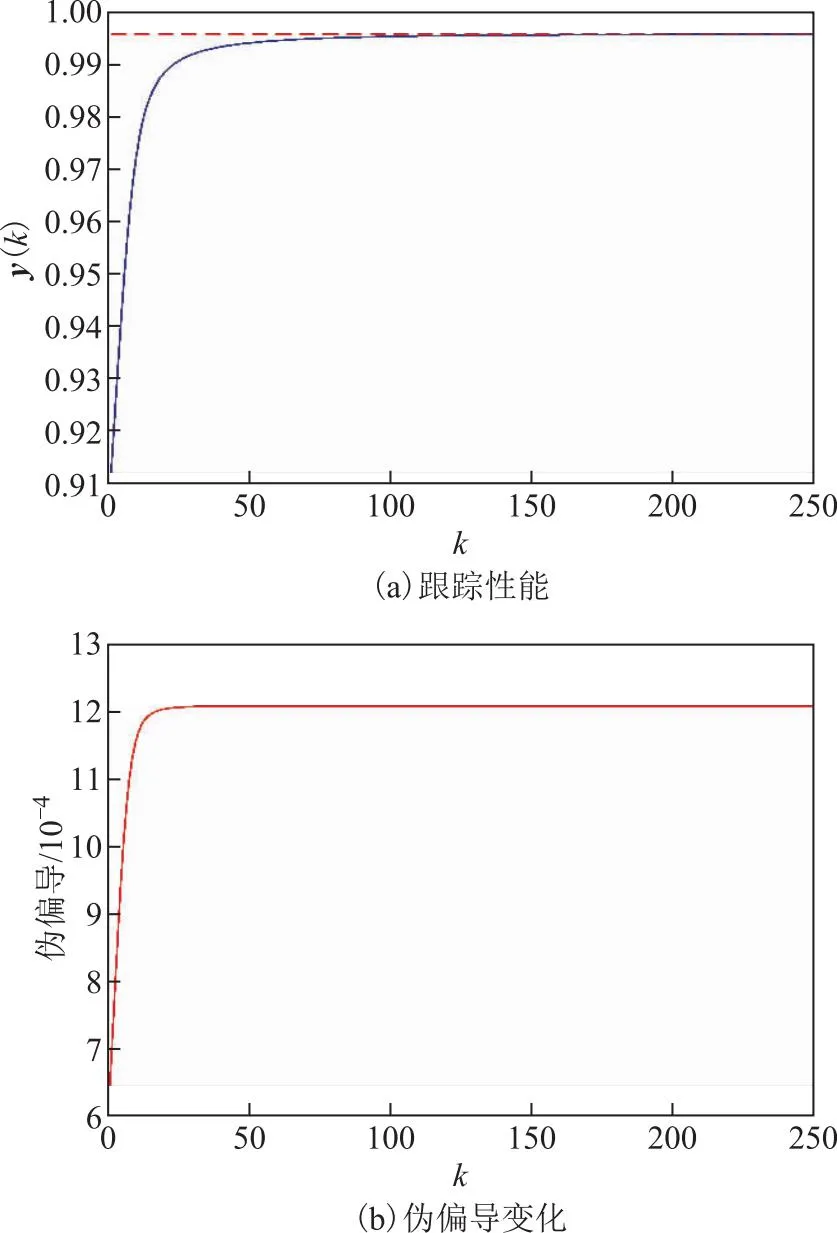
图8 丙烯塔SISO系统MFAC跟踪性能

3.1.2RBF-MFAC方案

保持丙烯塔SISO系统初值和MFAC初始参数设置不变。采用RBF神经网络实时整定四参数,设置RBF学习率ξ=0.1,动量因子α=0.07。按图2流程得到丙烯塔SISO系统现有MFAC控制跟踪效果和伪偏导变化趋势,如图9所示。图9(a)显示k=125时丙烯摩尔分数达到99.6%的目标。由图9(b) MFAC控制过程中伪偏导的变化趋势可见,相较于MFAC方案,RBF实时整定MFAC四参数时,伪偏导的变化更快,控制跟踪性能更好。

图9 SISO系统RBF-MFAC跟踪性能

图10为RBF-MFAC中四参数λ,μ,η,ρ的变化趋势。由图10可见:四参数初期变化较快,这是为了迅速达到期望值,提高跟踪性能;后期接近期望输出时,为避免超调,变化变缓。通过四参数的实时整定,RBF-MFAC自适应性增强。达到控制目标时,MFAC和RBF-MFAC操作调整次数分别为k=217和k=125,降幅为42.4%;仿真运行时间分别为1 189.0 s和694.5 s,降幅为41.6%(计算机为Win10系统,CPU为12th Gen Intel(R) Core(TM) i5-12400@2.50 GHz,RAM为16 GB DDR4 3 200 MHz)。

图10 SISO系统RBF-MFAC四参数变化趋势

3.2 MIMO系统

表2为丙烯塔当前操作的进料和产品组成,塔顶丙烯摩尔分数为94.6%,未达到合格品要求。

表2 丙烯塔MIMO系统进料和产品组成 x,%

在3.1节基础上,增加塔压调节。即输入u1为再沸器负荷,u2为塔顶压力P1;输出y1为塔顶丙烯摩尔分数,期望值yr1=99.6%,y2为丙烯产量D,期望值yr2=9 890 kg/h。故研究对象为二输入二输出的2I2O系统。图11为丙烯塔2I2O操作示意。

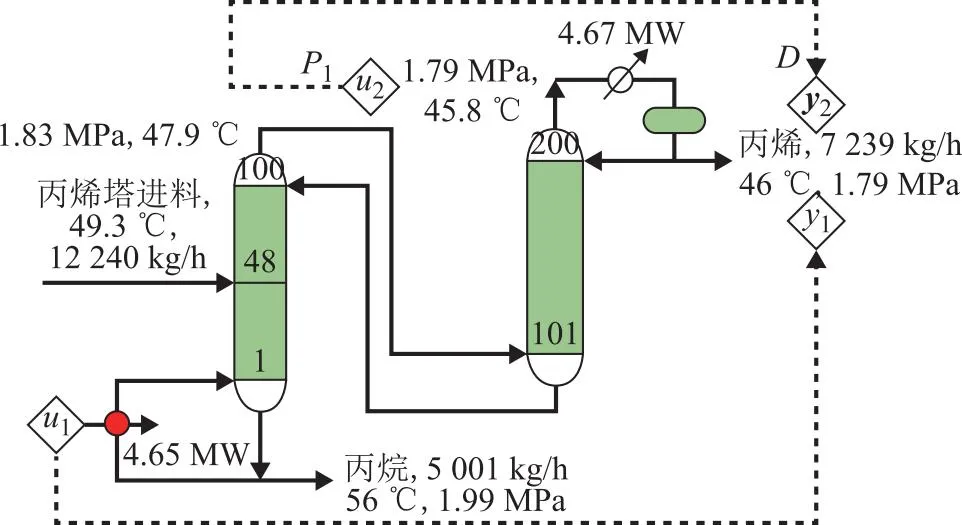
图11 丙烯塔2I2O操作示意

3.2.1MFAC方案

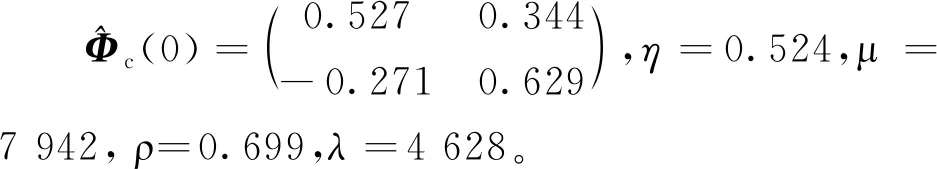
—yr1(k); —y1(k)

3.2.2RBF-MFAC方案

保持丙烯塔MIMO系统初值和MFAC初始参数设置不变。采用RBF实时整定MFAC参数,设RBF学习率ξ=0.1,动量因子α=0.07。实施图3流程,得到丙烯塔MIMO系统RBF-MFAC控制跟踪效果和伪偏导变化趋势,如图13所示。由图13可知,k=37时丙烯产量达标,k=42时两个目标均达标。

MIMO系统中yr1=99.6%和yr2=9 890 kg/h两个目标同时达到时,MFAC和RBF-MFAC操作调整次数分别为k=191和k=42,后者对前者的降幅为78.0%;仿真运行时间分别为1 048.8 s和246.4 s,降幅为76.5%。

图14为RBF-FMAC的λ,μ,η,ρ四参数变化趋势。从图14可以看出:控制初期四参数变化快,幅度相对较大,因此控制输入变化大,快速逼近期望目标;控制后期四参数变化缓慢,减小了对控制输入的影响,防止超调。

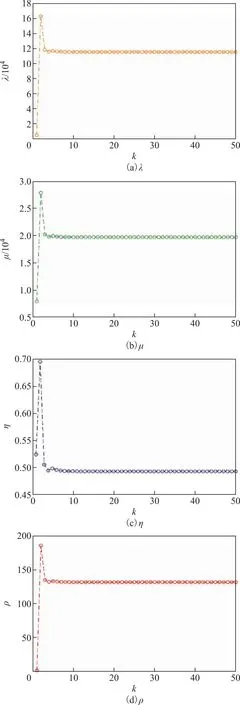
图14 MIMO系统RBF-MFAC四参数变化趋势

4 结 论

(1)针对现有无模型自适应控制算法中四模型参数恒定不变导致算法的跟踪性能和自适应性不强等问题,采用基于径向基函数的RBF神经网络,基于上两次调整的输入和伪偏导,以期望输出与实时输出差值为训练误差实时整定四参数。

(2)改进了现有SISO和MIMO离散时间非线性系统紧格式动态线性化无模型自适应控制流程,提出了RBF-MFAC控制算法。通过一个非线性系统验证了RBF-MFAC跟踪性能的优越性。

(3)将RBF-MFAC应用于某炼油厂0.30 Mt/a气分装置丙烯塔,其中I/O数据获取、RBF神经网络整定四参数、MFAC控制被集成在Maltab-Aspen软件平台中。计算结果表明:较现有MFAC控制,采用RBF-MFAC控制时丙烯塔SISO系统丙烯产品纯度达标调整次数减少42.4%,MIMO系统丙烯浓度和产量同时达标调整次数减少78.0%。说明RBF-MFAC控制过程跟踪性能相比MFAC明显增强。