台风登陆期间跨海大桥风-浪-流作用结构振动分析
2024-03-12沈忠辉
魏 凯,钟 茜,沈忠辉
(1.西南交通大学桥梁智能与绿色建造全国重点实验室,成都 610031; 2.清华大学水利水电工程系,北京 100084)
引言
台风是具有极强破坏性的低压天气系统,登陆时常常诱发狂风、巨浪、急流、风暴潮等自然灾害。跨海大桥由于跨度大、刚度低等特点,对台风登陆期间的风、浪、流作用十分敏感[1-2]。准确重现台风作用下复杂的海洋环境,并计算风、浪、潮、流荷载,分析桥梁结构的随机振动特性,是桥梁结构设计及安全运营的关键。
目前关于台风作用下海洋结构性能的研究主要基于现场实测或经验模型,但由于野外测量成本高、测量失效等原因,通过实测获取台风期间的海洋环境参数十分困难。然而,随着大气科学和海洋工程的发展,可通过数值模拟技术获取任意海域在台风登陆期间的风、浪、流、潮等要素。魏凯等[3-4]利用参数风场驱动波-流耦合模型实现了台风登陆期间的海洋环境模拟,并通过与实测数据进行对比,验证了该方法的准确性。
获得台风期间风、浪、流、潮等数据后,便可开展桥梁结构的随机振动分析。王浩等[5-6]基于实测数据研究了台风期间斜拉桥、悬索桥的抖振响应。TI等[7]对台风浪作用下大跨桥梁随机响应进行了模拟。除分析风或浪单独作用下桥梁结构的随机振动外,有学者还研究了风-浪联合作用下桥梁结构的动力响应。GUO[8]等开展了桥塔在风-浪联合作用下动力响应的模型试验,试验结果表明,当波浪周期位于结构的共振区时,风-浪联合作用对桥塔动力响应的影响显著。李永乐等[9]开展了风-浪联合作用下大跨度桥梁车-桥耦合振动分析,发现桥梁响应受波浪影响显著。刘高等[10]建立了车-桥-风浪流耦合动力系统,分析发现,与风场单独作用相比,风浪流耦合场能够激发桥梁产生更大幅度的横向和扭转振动,恶化列车运行安全性指标。但现有研究在考虑风、浪环境共同作用时常忽略台风期间风浪等环境参数间的相关性,与真实情况存在一定差异。
台风登陆时的风、波浪谱特性与良态风期间有显著区别。良态风的风谱假设大气层结稳定度为中性稳定。然而,LI等[11-12]对2008年台风“黑格比”期间的现场实测数据进行分析,发现台风期间大气并非一直保持中性稳定,与良态风环境存在差异。由于台风的强风作用,台风期间的波浪谱也与良态环境下的波浪谱不同。TI等[7]对台风“杜鹃”期间近岸桥址区的波浪进行野外观测,发现台风期间的波浪谱中风浪和涌浪共存,且风浪成分显著,存在多峰情形。WEI等[13]基于台风“苏迪罗”和“杜鹃”期间的波浪实测,提出了台风下波浪的参数波谱模型,并在模型中考虑了随台风时间变化引起的波谱变化。此外,实际跨海大桥中各墩处的波浪谱以及主波方向不同。DAI等[14]考虑了波高、波周期等波浪要素的变化,基于数值模拟研究了4.6 km长的fjord浮桥在波浪非一直激励作用下的动力响应,发现竖向响应受波浪非一致激励的影响显著。台风作用下的海洋环境数值模拟提供了精细的波流场信息,能为波浪非一致激励下桥梁的随机振动分析提供有力支撑。
因此,以某跨海公铁两用大桥为对象,通过引入数值模拟技术,基于台风混合模型及波-流耦合模型计算得到了台风“艾利”登陆期间的风、浪、潮、流荷载参数;计算台风登陆期间跨海大桥受到的风、浪、流、潮荷载,考虑台风下风谱及波浪谱与良态环境的不同,以及波浪的多点非一致激励;开展跨海斜拉桥风-浪-流作用随机振动分析,研究短期随机动力时程分析次数对响应统计特性的影响,并对不同时刻桥梁随机振动特性进行了计算,最后对桥梁短期极值响应的概率分布进行拟合。
1 台风登陆期间桥址区风-浪-流特性数值模拟
1.1 台风混合风场模型
台风模型是驱动波浪和风暴潮等复杂海洋环境的关键。本文采用由参数风场和背景风场叠加得到的混合风场来模拟台风风场,该风场的准确性已在以往研究中进行验证[15]。参数风场由于计算效率高且能满足工程精度,在台风灾害风险评估、风工程设计及台风期间波浪、风暴潮数值模拟中得到了广泛应用。基于中国气象局(CMA)提供的西北太平洋台风事件的信息(包括:时刻(6 h或3 h间隔)、强度等级、中心位置(经度和纬度)、中心最低气压和2 min平均最大持续风速等)开展台风参数风场的计算。台风参数风场由圆对称的梯度风场与台风移行风场叠加而成。
v(r)=vg(r)+vm(r)
(1)
式中,vg为梯度风场风速矢量;vm为移行风场风速矢量。本研究采用JAKOBSEN和MADSEN[16]的模型计算移行风场。
(2)
式中,vmc为台风中心移动速度矢量;RG(文中取500 km)为环境的长度尺度。为计算梯度风场,本研究采用应用较为广泛的HOLLAND[17]气压剖面描述台风的气压场。
(3)
式中,r为计算点到台风中心的距离;p(r)为台风径向气压;pc为台风中心气压;pn为外围环境气压,取1 010 hPa;Rm为最大风速半径;B为气压剖面形状系数。忽略地表摩擦,根据气压梯度力、科氏力及离心力平衡,得梯度风速为
(4)
式中,f=2Ωsin(Ψ)为计算位置处的科氏力系数;Ω为地球自转角速度;Ψ为纬度。Rm、B参数是Holland模型中关键的参数。本文采用经验公式计算Rm
Rm=Rk-0.4(pc-900)+0.01(pc-900)2
(5)
式中,Rk为经验常数,推荐值为40。B参数由最大持续风速计算。
(6)
Vgmax=sm/β
(7)
(8)
式中,ρa为空气密度,取为1.29 kg/m3;Vgmax为最大梯度风速,可由大气边界层顶部最大持续风速扣除移行风速获得(式(7)、式(8));β为从梯度风速转换到表面(10 m高度处)风速的折减因子,取0.9[15];sf为表面1 min平均最大风速,由CMA提供的2 min平均最大持续风速乘以1.03[18]转换得到;VtRe、VtRn分别为最大风速半径处的东向和北向的移行风速,由式(2)确定。需要注意的是,后文波流耦合模型需要表面10 min平均风速作为风场输入,因此需将计算的表面梯度风场和移行风场风速矢量转换为10 min平均风速矢量后叠加。1 min平均风速转换到10 min平均风速的转换系数取0.88[18]。
台风参数风场模型在台风中心附近具有较高的精度,但随着距台风中心距离增加,精度下降;相比台风参数风场模型,全球风场再分析产品在远离台风中心处,精度较高,在台风中心精度较差。为获得更精确的风场,将参数风场模型与CCMP全球再分析风场混合,得到混合风场模型。混合方式如下
(9)
式中,vHy为混合风场风速矢量;v为由台风参数模型确定的风速矢量;vccmp为CCMP风场风速矢量;α=(r-R1)/(R2-R1)为使参数风场与CCMP风场之间平滑过渡的系数,文中R1,R2分别取300 km和400 km。
1.2 SWAN+ADCIRC波流耦合模型
采用台风混合风场、气压场和全球海潮模型(TPXO)共同驱动SWAN+ADCIRC波流耦合模型以模拟台风期间的波浪、潮流等。SWAN是基于谱方程的第三代海浪模式,ADCIRC是目前应用广泛的潮流模式。SWAN+ADCIRC波流耦合模型中的SWAN模式和ADCIRC模式基于相同的非结构网格进行耦合计算[19]。ADCIRC将计算得到的风速、水位和流速数据传递给SWAN,SWAN根据ADCIRC提供的信息更新水深等与波浪计算相关的参数后计算波浪。然后,SWAN又将其计算出的波浪辐射应力传递给ADCIRC,ADCIRC又开始下一步的计算,以此循环,实现波流耦合模拟。该方法的有效性验证详见文献[15],本文不再赘述。
SWAN被广泛用于中小尺度海域的风浪生成及近岸演化模拟,其采用引入源项的动谱平衡方程为控制方程。
(10)
式中,N为波作用密度;σ为相对波频;θ为波向;cx和cy分别为波浪传播速度的x和y向分量;cσ和cθ分别为波浪在σ和θ空间的传播速度;S为用能量密度表示的源项。其中源项可考虑风浪成长、三波和四波相互作用、白帽耗散、底部摩擦耗散、水深变浅引起的波浪破碎、植被耗散、风浪遇到水下障碍物的绕射和反射、波浪绕射等过程。
ADCIRC模式是一种连续伽辽金、有限元、浅水模型,可用于求解一系列尺度的水位和流速,被广泛用于海洋、海岸、河口水动力计算。二维模式的ADCIRC,通过求解广义波动连续性方程和垂直积分动量方程获得水位和平均流速,并在计算中考虑了风、浪、潮汐和径流的影响。其控制方程[19]为
(11)
(12)
(13)
式中,H=ξ+h为总水深;ξ为从海平面起算的水位高度;h为静止海面下的水深;U、V为两个正交水平分量的平均流速;ps为水面大气压强;ρ0为水的密度;g为重力加速度;η为牛顿平衡潮汐势能;δ为地球有效弹性因子;τs,winds,τs,waves分别为由风和波浪引起的表面应力;τb为底部切应力项;M为侧向应力梯度;D为动力扩散项。
2 台风下风、浪、潮、流荷载计算方法
2.1 风荷载
桥梁所受风荷载由平均风和脉动风共同作用产生,其中脉动风速可根据风谱模型由谐波合成法生成。考虑静风荷载和抖振力作用,主梁单位长度受到的风荷载为
(14)

不考虑竖向风的作用,桥塔和桥墩横桥向单位长度上所受风荷载为
(15)
式中,b为桥塔或桥墩的断面迎风宽度;CDt[α(t)]为桥塔或桥墩在横桥向的风阻系数。桥塔的风阻系数根据LI等[21]基于CFD的数值模拟结果选取,上游桥塔CDt上取1.619,下游桥塔CDt下取-0.231。桥墩的风阻系数参考唐浩俊等[22]对不同柱间距的双柱式桥塔进行CFD数值模拟得到的结果进行近似考虑。上游桥墩阻力系数CDt上取0.347,下游桥墩阻力系数CDt下取0.829。同时,由于大跨度斜拉桥拉索数量多、长度长,在风荷载作用下受到的风荷载对全桥位移和内力贡献较大[23],故计算时考虑斜拉索受到的静风荷载。单位长度上,斜拉索受到的静风荷载为
(16)
式中,CDL[α(t)]为斜拉索在横桥向的风阻系数,根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》,取0.8。
台风期间风速变化较快,采用平均风分解法,将斜风分解成横桥向的余弦分量和顺桥向的正弦分量后,再根据现有的正风理论计算桥梁结构的响应[24],如图1所示。
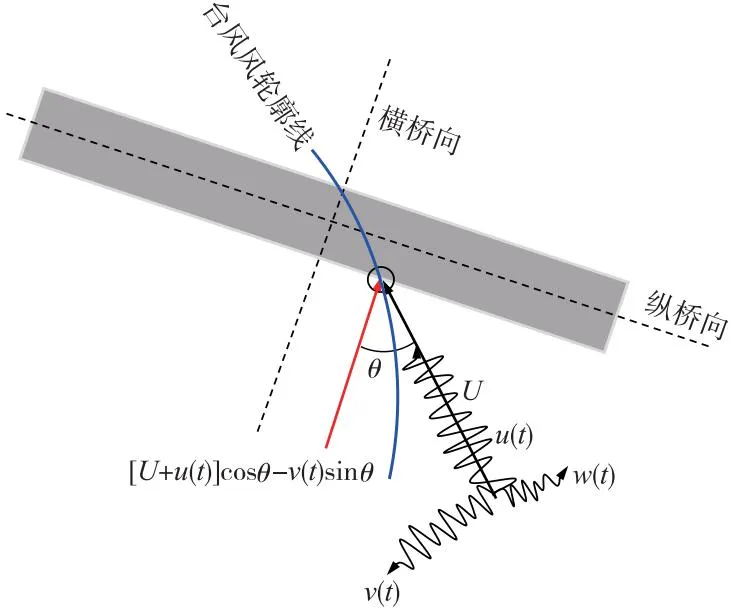
图1 斜风作用示意
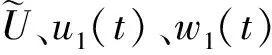
(17)
u1(t)=[U+u(t)]cosθ-v(t)sinθ
(18)
w1(t)=w(t)
(19)
风谱是脉动风计算的关键,而台风风环境与良态风环境的风谱存在差异。LI等[12]对2008年“黑格比”期间的近地层风场进行现场实测,发现台风的不同位置,台风的近地层湍流特征不同,并提出了台风不同位置的风谱模型。由于缺乏台风湍流特征的现场实测,本文采用LI等[12]提出的风谱模型计算台风期间的脉动风速,即顺风向风谱为
(20)
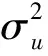
(21)
式中,u*为地表摩擦速度,可由下式计算
(22)
式中,κ为冯卡门常数,取0.4;z0为地面粗糙长度。
横风向风谱由von Karman[26]给出的顺风向风谱与横风向风谱的关系确定。由于台风期间并非为各向同性,需对von Karman[26]给出的关系式进行修正,根据TAO等[26]有
(23)
式中,Sv(n)为横风向风谱;k为修正系数,根据TAO等[26]的现场实测,本文取为0.25。同时,由于缺乏台风期间竖向湍流现场实测,本文采用Panofsky谱确定。
(24)
式中,Sw(n)为竖向风谱;σw为竖向风的统计方差,取良态风环境近地层根方差,即1.35u*。
2.2 波浪荷载
随机波浪可基于波浪谱采用线性叠加法进行模拟。获得随机波面后采用莫里森方程计算群桩受到的波浪荷载,作用于单个直立柱体任意高度z处的单位高度上的水平波浪力为
(25)
对于群桩基础,需要考虑波浪到达各桩之间的相位差及桩与桩之间的相互影响,包括遮挡效应和干扰效应。本文不考虑波浪到达各桩之间的相位差,根据FANG等[27],采用下式的遮挡系数(Kz)和干扰系数(KG)考虑桩与桩之间的影响。
Kz=1.0
(26)
(27)
式中,SG为相邻两桩之间的净距离;D为桩径。
大尺度承台上的水平波浪冲击荷载根据笔者提出的水平波浪荷载概率模型进行计算[28]。
F(t)=Fmaxp(t)
(28)
式中,Fmax为冲击峰值;p(t)为冲击的脉冲形状函数。
以往对各墩波浪荷载计算时,多采用相同的波浪谱,不考虑各墩的非一致激励或仅考虑各频率波到达各墩时在相位上的差异[2]。然而,实际跨海大桥各墩在波浪作用下可能处于更复杂的非一致激励波浪场中,各墩的波浪谱、浪向均可能不同。而基于台风下SWAN+ADCIRC波流耦合模拟结果,可获取各墩处的波浪信息,因此,采用各墩处的波浪谱、波向和水深对各墩处的波浪荷载进行计算以实现更复杂的非一致激励,如图2所示。图2中,Ai,Si,di(i=1,2,…,6)分别代表不同位置处桥墩、波浪谱、水深。
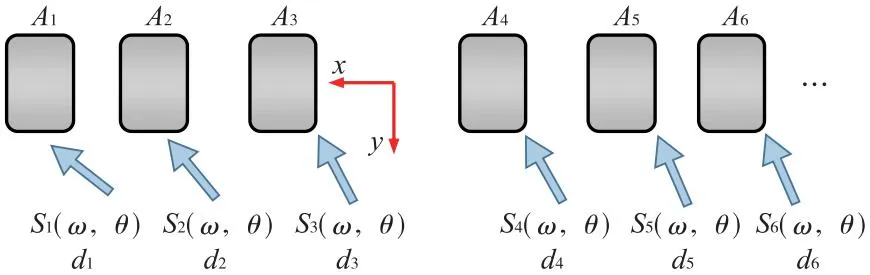
图2 波浪非一致激励示意
2.3 潮、流荷载
天文潮指海面受月球和太阳引潮力作用出现的周期性涨幅,而风暴潮是由于台风强烈的大气扰动引起海面异常升降现象。天文潮及风暴潮的共同作用会显著改变桥梁基础处的水深,影响波流荷载。基于数值模拟得到的结果,将天文潮和风暴潮两者叠加后造成的水位变化考虑到水深的计算中。
同时,采用JTS 144—1—2010《港口工程荷载规范》计算群桩水流力,即
F(t)=0.5ρAcCwV(t)2
(29)
式中,Ac为计算构件在海流垂直平面上的投影面积;Cw为海流阻力系数,圆形断面取为0.73;V(t)为海流流速,采用下式构造流速剖面
王国:① 以国王为国家元首的国家;② 借指管辖的范围或某种境界;③ 借指某种特色或事物占主导地位的领域。
(30)

3 工程背景与结构建模
3.1 工程背景
以某跨海公铁两用大桥的主航道桥为对象,对该桥在台风登陆期间的风-浪-流多灾害作用下的随机振动进行分析。该航道桥全长1 190 m,为双索面双塔斜拉桥,其中桥塔为H形桥塔,塔高219.5 m。各跨跨径为(133+196+532+196+133) m。跨径布置及构造如图3所示。

图3 实例桥梁构造(单位:cm)
桥梁主塔、辅助墩、边墩基础均采用高桩承台结构。主塔桩基础采用φ3.4 m钻孔灌注桩,边墩和辅助墩桩基础采用φ2.8 m钻孔灌注桩。主梁为倒梯形桁梁,宽36.5 m,高15 m。主梁距平均海平面94.8 m,主塔顶距平均海平面232 m。图4展示了卫星航拍的桥址区,桥梁走向与正西向的夹角为57°。

图4 元洪航道桥卫星航拍(单位:m)
3.2 跨海大桥有限元模型
采用有限元软件ANSYS建立有限元模型。主梁、主塔、桥墩、基础采用BEAM4单元,拉索采用LINK8单元。全桥采用半漂浮体系,主塔、桥墩采用C55混凝土,桩、承台采用C40混凝土。为简化桩土相互作用,采用等效嵌固模型计算有效桩长,即局部冲刷线下4倍桩径处固结。采用cp命令耦合边墩、辅助墩和主梁横桥向和竖向位移,N03主塔与主梁纵桥向、横桥向和竖向位移,N04主塔和主梁横桥向和竖向位移。图5中展示了加载台风风、浪、流荷载。

图5 全桥有限元模型
全桥前10阶动力特性分析结果如表1所示。

表1 全桥前10阶振动特征及振型描述
采用ANSYS的完全法(Full)进行动力响应分析,阻尼考虑瑞利(Rayleigh)阻尼,阻尼比设置为0.5%。需要说明:后文计算结果的坐标系为图4中坐标系,主梁横向位移为负时,位移朝向内侧海域。
3.3 强台风“艾利”
在以往研究中,笔者基于台风下风-浪-流模拟技术,模拟了1990—2018年对该桥有重要影响的58次历史台风事件[15]。其中,2004年18号台风“艾利”造成了桥址最大台风风和波浪。台风“艾利”于2004年8月18日上午在雅蒲岛西北方向生成,于8月25日晚在福建登陆,路径如图6所示。登陆时中心气压为975 hPa,中心最大风力达12级(35 m/s)。本文选取其作为算例,对其登陆期间的海洋环境进行模拟。同时,以得到的环境要素为基础,开展台风作用下跨海大桥随机振动分析,并研究其随机振动特性。
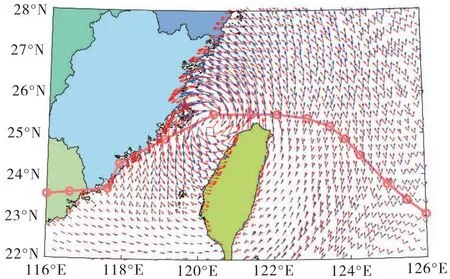
图6 台风“艾利”下风、浪模拟结果
4 台风下桥梁结构振动分析
4.1 台风“艾利”下桥址区环境模拟结果
图6给出了强台风“艾利”下算例所在海域最大风速时刻的风、浪模拟结果。红色箭头表示风场,蓝色箭头表示波浪场(箭头的长度为归一化之后的大小)。从模拟结果中可以看出,波向与风向相关性强,桥位处的风、浪间夹角较小。
图7为模拟得到的算例桥墩、桥塔及跨中的风、浪、流演变过程。虚线表示变量方向、实线表示变量值,t1、t2、t3、t4分别为桥位经历的最大风速时刻(FEW位置)、FEW位置风速与横桥向夹角最小时刻、BEW位置风速与横桥向夹角最小时刻及跨中(KZ)最大波高时刻(BEW位置)。其中,风速为10 m高度处的10 min平均风速,流速为垂直积分的平均流速。图7还展示了跨中最大波高时刻,模拟得到各墩处的波浪谱,由图可知,波高、流速、波向、流向受水深影响显著,各墩和塔处的波高、流速、波向、流向存在一定差异。表2为各桥墩在t1~t4时刻的潮位变化。
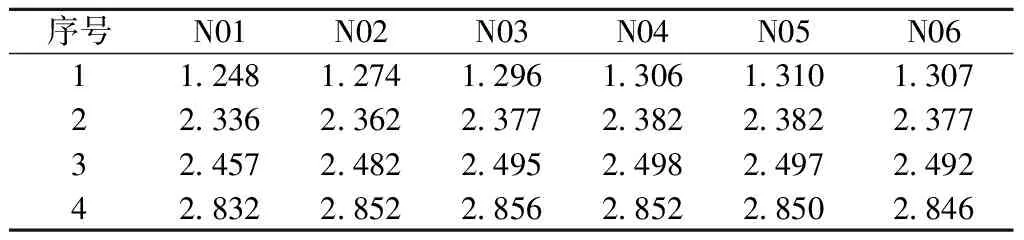
表2 t1、t2、t3、t4时刻各墩处潮位 m

图7 台风“艾利”期间各墩、桥塔及跨中风、浪、流、潮演变过程
4.2 短期时程分析次数的影响
短期时程分析的结果具有明显的变异性,为探明其变异性,本节以台风“艾利”登陆期间t2时刻为例,开展了100次短期随机模拟。与WANG等[29]一致,短期时程分析的时长选为10 min。
为说明短期时程分析的变异性,基于重抽样方法(Bootstrap方法[30]),定义变异因子为:95%置信区间上下界分别与均值之间差值的平均值比上均值。例如,对以上计算的100组结果(均值、标准差等),进行M次抽样,每次抽取N(N≤100)组结果。则就有M个N组结果的均值。对M个值进行排序,就可确定95%置信区间,由此N组结果均值的变异因子即可求出。
采用Bootstrap方法[30],进行10 000次抽样N(N≤100)个短期随机模拟,计算得到跨中横向位移标准差、跨中竖向位移标准差的变异因子随N的变化,如图8所示。其中,N个短期随机模拟内事件可重复抽样,即认为只有进行无限个短期随机模拟,其变异性才会为0。为解释本处定义的变异因子的含义,以跨中横向位移标准差为例,当短期样本集合为30时(比拟模拟时长为5 h),变异因子为0.06。这说明进行30次短期分析(5 h)得到的跨中横向位移标准差(30次的平均值),95%的可能性位于长期统计标准差的±1.06倍范围内(σ5h∈σ长期±0.06σ长期)。

图8 跨中横向位移、竖向位移标准差随短期模拟次数的变异性
由图8可知,随着模拟集合数量增加(模拟时间的增加),变异因子的下降斜率越来越小,当N>12(比拟模拟时长为2 h),增加短期模拟次数(模拟时长),对改善统计特征的变异性已不在乐观。为更精确描述结构长期响应的统计特征(均值和标准差),下文对每个工况进行30次重复模拟(比拟模拟时长为5 h)。每个工况的统计特征(均值和标准差)采用30次模拟的均值作为代表。
4.3 不同时刻桥梁结构振动特性
为描述台风“艾利”登陆期间的桥梁随机振动特性,本文分别计算了t1、t2、t3、t4时刻,模拟时长为10 min的桥梁随机动力响应。其中,最大风速时刻,桥梁位于台风的FEW位置,跨中最大波高时刻位于台风的BEW位置。基于前一节的研究结果,为考虑风荷载、波浪荷载由于脉动成分引起的变异性,对每一组风、浪、流、潮作用下都进行30次结构响应计算。
最大风速时刻(t1),30次10 min风、浪、流、潮作用下的响应结果为:跨中横向位移均值为-0.258 7 m、标准差为0.136 8 m;跨中扭转角均值为-0.001 7rad、标准差为0.000 1 rad;N03塔顶横向位移均值为-0.064 9 m、标准差为0.032 3 m;N03塔底横向剪力均值为-7.4×106N、标准差2.5×106N。
以t1为基准,计算t1,t2,t3,t4时刻的桥梁动力响应的相对大小(Rti/Rt1)如图9所示,其中包括:主梁跨中横向位移(B1)、跨中扭转角(B2)、N03塔顶横向位移(B3)、N03塔底横向剪力(B4)。

图9 响应均值及标准差
由图9可知,t2时刻的位移相对较大,此时跨中横向位移均值比最大风速时刻(t1)增加了12.5%,标准差增加了8.4%。这是由于t1至t4时刻,风速变化不大(35.22~34.23 m/s),同时波高大小变化也较小(跨中5.70~6.22 m),然而风向、波向变化显著(风向22.4°~14.4°、跨中波向-10.7°~10°),因此台风“艾利”期间最大响应可能在风速与横桥向夹角最小时刻(t2)附近取到。这也说明在台风期间考虑风向、波向变化的重要性。
为说明台风登陆期间桥梁的动力响应特性,以t2时刻为代表,图10展示了B1、B2、B3、B4在单独风荷载、单独波浪荷载及风-浪-流多灾害作用下的响应幅值谱。
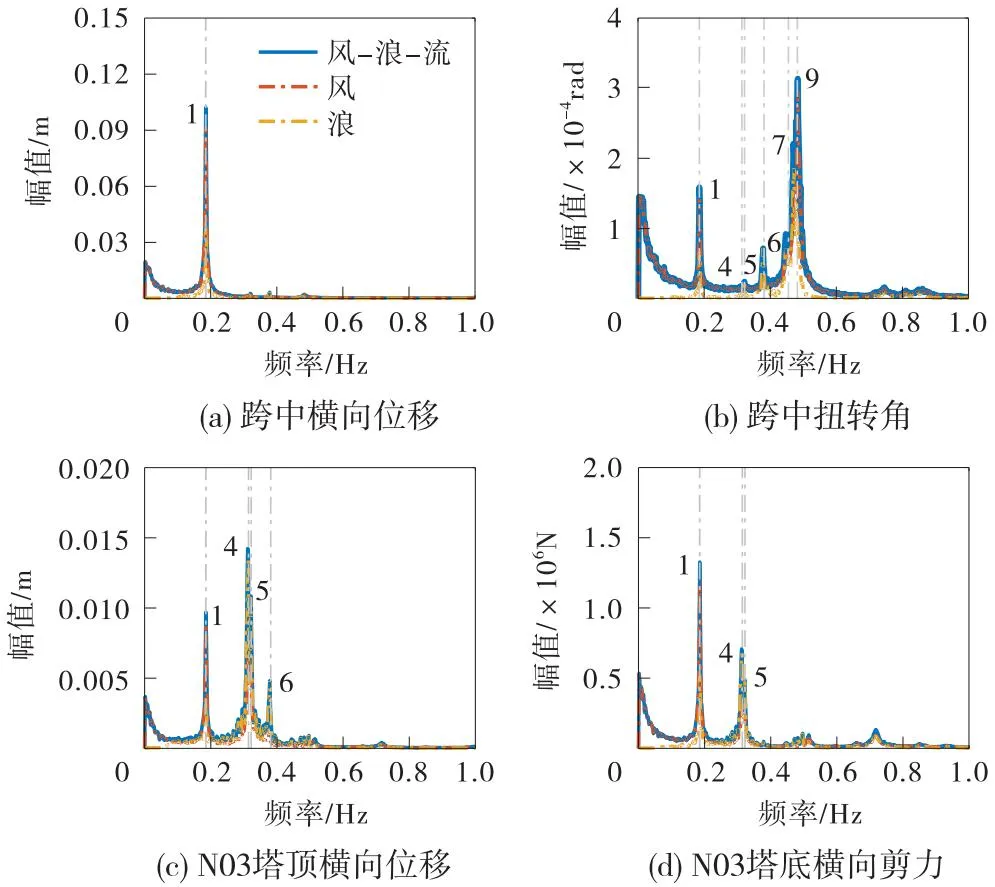
图10 桥梁的动力响应幅值谱(30组频谱的平均谱)
由图10可知,风荷载对主梁跨中横向位移和扭转角影响显著,而波浪荷载对N03塔顶横向位移贡献较大,这主要与算例采用的双柱式桥塔有关。根据LI等[21]开展的CFD数值分析,由于受到上游塔柱的干扰,下游塔柱的阻力系数为负,桥塔整体所受风荷载较小。同时,相对1阶振动,波浪引起的高阶振动明显。在单独波浪荷载作用下,贡献N03塔顶横向位移的模态主要为4~6阶(>0.3 Hz)。由于台风的强风作用,台风期间的波浪谱风浪成分显著(>0.1 Hz),如图7所示,因此,对于高阶振动参与显著的大跨桥梁,忽略台风期间波浪谱的变异(显著的风浪成分),无疑会低估桥梁的动力响应。
4.4 桥梁极值响应概率分布
为推求台风“艾利”期间的结构极值响应,对响应均值和标准差都较大的t2时刻下的极值响应进行分析。由于较多的数据量开展概率分布拟合具有更高的可信度,为推求较小概率下的结构极值响应,利用4.2节中100次t2时刻的短期时程分析,并对短期时程分析极值的概率分布进行拟合。图11展示了分别采用正态分布和广义极值分布拟合得到的结果。
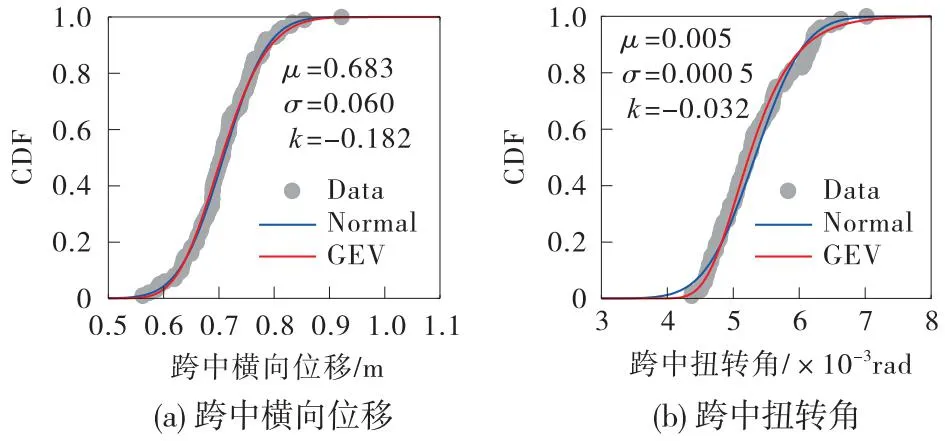
图11 短期极值分布及分布拟合
短期极值的分布与正态分布和广义极值分布吻合都较好,同时都通过了置信水平为95%的K-S检验。然而,对整体而言(B1、B2),广义极值分布对描述结构响应极值相对较好。
利用短期时程分析极值分布进行概率外推,可以得到响应极值与超越概率之间的关系,如图12所示。由图12可知,当超越概率为0.000 1时(即进行10 000次短期时程分析,得到的最大响应),拟合的跨中横向位移值为0.95 m,跨中扭转角值为0.008 8 rad。

图12 响应极值与超越概率之间的关系
5 结论
本文利用台风混合风场及波-流耦合模型模拟了台风期间的海洋环境,充分考虑台风环境的特点,开展了台风期间跨海大桥的振动特性分析。通过计算分析,主要结论如下。
(1)开展台风登陆期间随机振动分析时,考虑风向、波向变化十分重要。根据算例分析,主梁跨中横向位移和扭转角受风荷载影响显著,而桥塔塔顶横向位移则受波浪荷载影响显著。
(2)在随机振动分析时,开展30次10 min短期分析的结果可以有效描述长期分析的均值,在保证精度的同时,提高计算效率。
(3)根据算例桥梁结构振动分析,其在台风登陆期间的10 min随机振动短期响应极值服从广义极值分布,基于短期极值分析,可计算该台风期间的极值响应。
需要注意的是,本文研究的台风风谱采用了历史台风实测结果,未考虑台风风谱的变异性。同时,结构动力分析均为线性范畴,未考虑材料非线性的影响。上述研究有待未来深入开展。本文研究方法和相关分析结果可为台风下跨海大桥实时预警及监控提供理论支撑。
