Intelligent Solution System for Cloud Security Based on Equity Distribution:Model and Algorithms

Sarah Mustafa Eljack ,Mahdi Jemmali ,Mohsen Denden ,Mutasim Al Sadig ,Abdullah M.Algashami and Sadok Turki

1Department of Computer Science and Information,College of Science at Zulfi,Majmaah University,Al-Majmaah,11952,Saudi Arabia

2Department of Computer Science,College of Computing and Informatics,University of Sharjah,Sharjah,United Arab Emirates

3Higher Institute of Computer Science and Mathematics,University of Monastir,Monastir,5000,Tunisia

4Mars Laboratory,University of Sousse,Sousse,Tunisia

5Department of Logistic and Maintenance,UFR MIM at Metz,University of Lorraine,Metz,France

6Department of Computer and Information Technologies,College of Telecommunication,and Information Riyadh CTI,Technical and Vocational Training Corporation TVTC,Riyadh,12464,Saudi Arabia

7Department of Computer Science,Higher Institute of Applied Sciences of Sousse,Sousse University,Sousse,4000,Tunisia

ABSTRACT In the cloud environment,ensuring a high level of data security is in high demand.Data planning storage optimization is part of the whole security process in the cloud environment.It enables data security by avoiding the risk of data loss and data overlapping.The development of data flow scheduling approaches in the cloud environment taking security parameters into account is insufficient.In our work,we propose a data scheduling model for the cloud environment.The model is made up of three parts that together help dispatch user data flow to the appropriate cloud VMs.The first component is the Collector Agent which must periodically collect information on the state of the network links.The second one is the monitoring agent which must then analyze,classify,and make a decision on the state of the link and finally transmit this information to the scheduler.The third one is the scheduler who must consider previous information to transfer user data,including fair distribution and reliable paths.It should be noted that each part of the proposed model requires the development of its algorithms.In this article,we are interested in the development of data transfer algorithms,including fairness distribution with the consideration of a stable link state.These algorithms are based on the grouping of transmitted files and the iterative method.The proposed algorithms show the performances to obtain an approximate solution to the studied problem which is an NP-hard(Non-Polynomial solution)problem.The experimental results show that the best algorithm is the half-grouped minimum excluding(HME),with a percentage of 91.3%,an average deviation of 0.042,and an execution time of 0.001 s.

KEYWORDS Cyber-security;cloud computing;cloud security;algorithms;heuristics

1 Introduction

With the improvement of computer and communication technology and the increasing need for human quality of life,intelligent devices are growing in popularity.Internet applications are growing in diversity and complexity due to the development of artificial intelligence algorithms and communication technologies.Traditional cloud computing,which is used to support general computing systems,can hardly satisfy the needs of IoT(Internet of Things)and mobile services due to location unawareness,bandwidth shortage,operation cost imposition,lack of real-time services,and lack of data privacy guarantee.These limitations of cloud computing pave the way for the advent of edge computing.This technology is believed to cope with the demands of the ever-growing IoT and mobile devices.The basic idea of edge computing is to employ a hierarchy of edge servers with increasing computation capabilities to handle mobile and heterogeneous computation tasks offloaded by the low-end (IoT) and mobile devices,namely edge devices.Edge computing has the potential to provide location-aware,bandwidth-sufficient,real-time,privacy-savvy,and low-cost services to support emerging innovative city applications.Such advantages over cloud computing have made edge computing rapidly grow in recent years.Cloud computing consists of many data centers that house many physical machines(hosts).Each host runs multiple virtual machines(VMs)that perform user tasks with different quality of service (QoS).Users can access cloud resources using cloud service providers on a pay-as-you-go basis.

The IoT environment associated with the cloud computing paradigm makes efficient use of already available physical resources thanks to virtualization technology.Thus,multiple healthcare service users(HCS)can store and access various healthcare resources using a single physical infrastructure that includes hardware and software.One of the most critical problems in healthcare services is the task scheduling problem.This problem causes a delay in receiving medical requests in the healthcare service by users in cloud computing environments.

In this work,a new model was developed to store user data with fair distribution in cloud virtual machines.The used method can reinforce the security of the stored data.Two types of information are distinguished in this model.The first type is the data flow generated by users.It is random data because time and size are unknown.The second one is the control information or mapping information gathered by the collector agent and analyzed by the monitor agent according to the security levels.The scheduler receives the random user data which represents the main input for our algorithms and the regular information from the monitor agent which represents the second entree parameters for six algorithms.In this paper,the two presented agents are proposed in the model description and explained as part of our global model.The interaction of these agents with the scheduler will be treated in future work.This paper focused on the development of algorithms for equity distribution.For each data flow,developed algorithms should indicate the appropriate virtual machine and ensure a fair distribution of all incoming data.The task scheduling algorithms in the literature are used to reach an objective like minimizing the Makespan or latency or other well-known objectives.In this paper,a new objective is proposed.In addition,novel algorithms based on the grouping method are developed and assessed to show their performance.Consequently,the proposed algorithms can be reformulated and applied to solve traditional scheduling problems like parallel machines flow shops,or other hard problems.The main contributions of this paper are:

• Developing a new model for efficient file storage.

• Develop algorithms for equity distribution related to the virtual machines in the cloud environment.

• Minimize the risk of losing data by ensuring an equity distribution for the virtual machines.

• Compare the efficiency of the proposed algorithms and their complexity.

This paper is structured as follows.Section 2,is reserved for the related works.Section 3 presents the study background.In Section 4,the proposed algorithms are detailed and explained.The experimental results are discussed in Section 5.Finally,the conclusion is given in Section 6.

2 Related Works

Some classical scheduling techniques,such as first-come-first-served(FCFS),round robin(RR),and shortest job first (SJF),can provide scheduling solutions.Still,the scheduling problem is NPhard,which makes cloud computing difficult.It fails to meet the needs of programming [1].Since traditional scheduling algorithms cannot solve NP-hard optimization problems,modern optimization algorithms,also called meta-heuristic algorithms,are used nowadays instead.These algorithms can generate optimal or near-optimal solutions in a reasonable time compared to traditional planning algorithms.Several metaheuristic algorithms have been used to deal with task scheduling in cloud computing environments.For example,a new variant of conventional particle swarm optimization(PSO),namely his PSO(RTPSO)based on ranging and tuning functions,was proposed in[2]to achieve better task planning.In RTPSO,the inertia weight factors are improved to generate small and large values for better local search and global searches.RTPSO was merged into the bat algorithm for further improvement.This variant he named RTPSO-B.

In [3],the authors developed a task scheduling algorithm for bi-objective workflow scheduling in cloud computing based on a hybrid of the gravity search algorithm(GSA)and the heterogeneous earliest finish time(HEFT).This algorithm he called HGSA.This algorithm is developed to reduce manufacturing margins and computational costs.However,GSA sometimes does not work accurately for more complex tasks.The bat algorithm(BA)is applied to address the task scheduling problem in cloud computing with objective features to reduce the overall cost of the workflow[4,5].On the other hand,BA underperformed in higher dimensions.Several papers treated load balancing in different domains.In finance and budgeting [6–9],storage systems [10],smart parking [11],the network[12],and parallel machines[13].The authors in[14]proposed two variants of PSO.The first,called LJFPPSO,is based on initializing the population using a heuristic algorithm known as the longest job to fastest processor(LJFP).On the other hand,the second variant,MCT-PSO,uses the MCT(minimum completion time)algorithm to initialize the population and improve the manufacturing margin,total execution time,and non-uniformity when dealing with task scheduling problems in the cloud.

This answer intended to limit the general execution value of jobs,at the same time as maintaining the whole of entirety time inside the deadline [15].According to the findings of a simulation,the GSO primarily based mission scheduling (GSOTS) set of rules has higher consequences than the shortest mission first (STF),the most essential mission first (LTF),and the (PSO) algorithms in phrases of reducing the whole of entirety time and the value of executing tasks.There are numerous different metaheuristics-primarily based mission scheduling algorithms inside the cloud computing environment,which include the cuckoo seek a set of rules(CSA)[16],electromagnetism optimization(EMO)set of rules[17],sea lion optimization(SLO)set of rules[18],adaptive symbiotic organisms seek(ASOS)[19],hybrid whale optimization set of rules(HWOA)[20],synthetic vegetation optimization set of rules(AFOA)[21],changed particle swarm optimization(MPSO)[22],and differential evolution(DE)[23–27].In the same context,other research works are developed[28–30].

The algorithms developed in this paper can be extended to be used for the subject treated in[31–35].The techniques for machine learning and deep learning can be utilized to develop new algorithms for the studied problem [36].The Prevention Mechanism in Industry 4.0,the vehicular fog computing algorithms,and the Scheme to resist denial of service(DoS)can also be adapted to the novel constraint of the proposed problem[37–40].

According to literature research.Most of the heuristics and approaches developed to schedule data flows focus on minimizing processing time and optimizing resources.There is not much research that integrates the scheduling problem and the data security problem.By developing our approach,we believe we can integrate certain security parameters into the scheduling algorithms.We believe that the combination of the two techniques saves data processing time.In this article,we succeeded in developing the best scheduling algorithms by considering the security parameters (Collector and Monitor Agents) as constants.Our work continues to develop selection algorithms (trusted paths)and integrate them with those recently developed.

In general,Cloud environments can have many internal and external vulnerabilities such as Imminent risk linked to a bad configuration,possibly bad partnership/deployment strategy,and unauthorized access to resources,which increases the attack surface.To keep this environment accessible and secure,access controls,multi-factor authentication,data protection,encryption,configuration management,etc.,are essential.Our goal is to place cloud data streams in the right places while minimizing data security risks.

3 Study Background

Nowadays,the cloud environment has become the primary environment to run applications that require large capacities.Several areas use the cloud because of its scalability,fast services,and “we pay for what we consume”.Data flow planning in the cloud aims to minimize the overall execution time.It consists of building a map of all the necessary components to achieve tasks from source to destination.This process is called task mapping.The cloud environment faces many challenges,such as cost and power consumption reduction of various services.The optimization of the cost is studied in[41–44].Recently,many international companies have ranked security[45–47]as the most difficult parameter to achieve in the cloud and the first challenge for cloud developers and users.In the literature,several heuristics and meta-heuristics have been developed to optimize cost,processing time,and distribute workflows and tasks [48–50].Heuristics and algorithms for planning workflow in a cloud environment,taking into account security parameters,are not extensively developed.The security process includes an additional process time.The objective of our research is to develop new heuristics to reduce unused or mismanaged network resources.The developed model consists of periodically collecting information on the state of links,and intermediate nodes in the network,using a collector agent.This information is analyzed and subsequently classified using a monitor agent according to the level of confidence.The novel model is based essentially on three agents,as illustrated in Fig.1.

“Collector Agent”has the role of the collector to gather all possible information on the global state of the network.The collector agent scans all available resources and collects information about the state of the cloud virtual machine and the network link.This component translates this information to the monitor which processes it,analyzes it and decides on the security level of each link,and transmits it to the scheduler.

The information generated is an additional input for the scheduler which must take it into account in each calculation.Several other works can be considered[51–53].

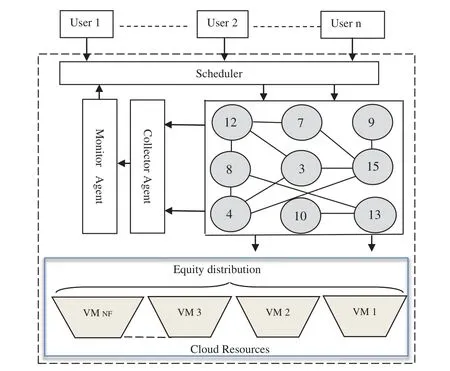
Figure 1:Model for the cloud computing environment

Information related to the security level will be treated specially.The second agent is the“Monitoring agent”which must analyze received information,estimate the risk levels on each section of the network,and decide whether the final state of the network is a downlink,low-risk or fair-link,or high-risk link(See Fig.2).The Scheduler component run the best-proposed algorithm to make a final decision about workflow dispatching.Users generate an arbitrary size of data flow.Finally,the“Cloud resources”component represents the set of virtual machines(storage servers or Hosts,etc.).

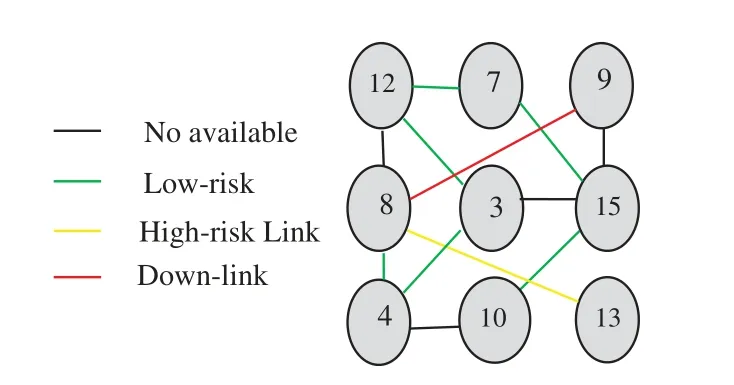
Figure 2:Monitoring agent decomposition

The scheduler should define the destination of each file ensuring the load balancing of the final state of the virtual machines.The network path state is described in Fig.2.In this work,we focus on the role of the scheduler component that calls the best-proposed algorithm to solve the problem of dispatching files that must be executed by the virtual machines.The two presented agents are proposed in the model description and explained as part of our global model.Algorithms for the two agents will be treated in future work.In this paper,the objective is to propose several algorithms to solve the scheduling problem of transmission of files to different virtual machines ensuring equity distribution.To do that,the gap of the used spaces between all virtual machines must be searched.This gap is denoted byGpVand given in Eq.(1):

The variable descriptions are presented in Table 1.The objective is the minimizeGpV.This problem is already proved as an NP-hard problem in[10].

Table 1: Description of all used notations

Example 1 may clarify the objective proposed in this paper.

Example 1

Assume that eight files must be transmitted to three virtual machines.In this case,Nf=8 andNv=3.The size filessfjfor the filefj∀j={1,...,Nf}are presented in Table 2.

Table 2: Size of the eight files

This example used two algorithms to explain the proposed problem.The first algorithm is the shortest size first(SSF).This algorithm is based on the sorting of all files according to the increasing order of their size.After that,the scheduling of the files will be done one by one on the virtual machine that has the minimumTvi.The second algorithm is the longest-size file algorithm(LSF).Firstly,the files are sorted according to the decreasing order of their sizes.Next,the first file will be assigned to the first virtual with the minimumTvivalue and so on,until the scheduling of all files.ForSSF,files{1,3,7}are transmitted to the first virtual machine,files{2,4,6}are transmitted to the second virtual machine,and files{5,8}are transmitted to the second virtual machine.Consequently,the loadTv1inV1,Tv2inV2,andTv3inV3are 31,39,and 20,respectively.Thus,Tvmin=20.So,theGpVvalue is=(31-20)+(39-20)+(20-20)=30.In this case,the gap between the used spaces between all virtual machines is 30.Now,it is crucial to find another schedule that gives a better solution than the latter result.This means that find a schedule with a minimum value ofGpV.In this context,the algorithmLSFis applied.This algorithm gives the schedule as follows:files{5,6}are transmitted to the first virtual machine,files{1,3,7}are transmitted to the second virtual machine,and files{2,4,8}are transmitted to the second virtual machine.Consequently,the loadTv1inV1,Tv2inV2,andTv3inV3are 29,31,and 30,respectively.Thus,Tvmin=29.So,theGpVvalue is(Tvi-Tvmin)=(29-29)+(31-29)+(30-29)=3.In this case,the gap of the used spaces between all virtual machines is 3.This schedule is better than the first one.A gain of 27 units is reached after applying the second algorithm.

To ensure a fair distribution,the algorithms must always calculate the difference in capacity between the virtual machines also called the gap(the gap is the unused space in each virtual machine).The main role of algorithms is to minimize the gap(capacity)between different virtual machines.The scheduler must then transfer a flow of capital data to the appropriate virtual machine(the one which must minimize the difference between the different virtual machines).In this way,data stability is more secure and several tasks that may occur such as data migration are avoided.Data stability means even less risk.On the other hand,if we consider that the states of the links are stable,this means that there is no other constraint to be taken into account by the scheduler,it must ensure a fair distribution in the first place.If the link states are not stable,other factors must be considered in the calculation of the scheduler since the virtual machines will not be“judged”according to their level of use but also according to the level of risk.This is what we are currently developing.

The main idea is to forward the data stream to the appropriate cloud virtual machines.In the developed model,two new components are introduced which are the collector agent and the monitor agent.The collector agent collects information about the state of the network(nodes and links),mainly security information(denial of service,downlinks,virtual machines at risk,etc.).This information will be transmitted to the surveillance agent who traits this information,decides the risk level degree,and transmits it to the scheduler.The scheduler must consider the decision of the monitor agent as input and re-estimate its new decision according to the new considerations.

4 Proposed Algorithms

In this section,several algorithms to solve the studied problem are proposed.These algorithms are based on the grouping method.This method consists of dividing the set of files into two groups.After that,several manners and variants are applied to choose how to schedule the files on the virtual machines between the first group and the second one.Essentially,seven-based algorithms are proposed.The proposed algorithms are executed by applying four steps.Fig.3 shows the steps of the objective reached by algorithms.The first step is the “Objective”which is the load-balancing schedule.The second step is the mathematical formulation to reach the load balancing.The third step is minimizing the load gap by reaching the solution.The fourth step is the analysis of the performance of each solution obtained by the proposed algorithms.

4.1 Longest Size File Algorithm(LSF)

Firstly,the files are sorted according to the decreasing order of their sizes.Next,the first file will be assigned to the first virtual machine with minimumTvivalue,and so on,until the scheduling of all files.The complexity of the algorithm isO(nlogn).

Figure 3:Steps of the objective reached by algorithms

4.2 Half-Grouped Classification Algorithm(HGC)

This algorithm is based on dividing the set of files into two groups.Initially,the two groups are empty.The number of files in the first group,G1isn1=.While the number of files in the second group,G2isn2=Nf-n1.In fact,G1={f1,...,fn1} etG2={fn1+1,...,fNf} whereF={f1,...,fNf}.The proposed algorithm uses three variants.For each variant,a solution is calculated,and the best solution is picked.In the first variant,there any sort of changes to the setFis made.After creating the two groups,G1andG2,two manners are applied to scheduling files.The first is to schedule all files inG1.After that the files inG2are scheduled.The second manner is to schedule all files inG2.After that,all files inG1are scheduled.The solution is calculated for this first variant.In the second variant,the files inFare sorted according to the decreasing order of their sizes.After creating the two groups,G1andG2,two manners are applied to scheduling files.The first is to schedule all files inG1.After that,all files inG2are scheduled.The second manner is to schedule all files inG2.After that,all files inG1are scheduled.The solution is calculated for this first variant.In the third variant,the files inFare scheduled according to the increasing order of their sizes.After creating the two groups,G1andG2,two manners are applied to scheduling files.The first is to schedule all files inG1.After that,all files inG2are scheduled.The second manner is to schedule all files inG2.After that,all files inG1are scheduled.The solution is calculated for this first variant.Denotes byDCs(A),the procedure that accepts a set of elements as input and sorts these elements according to the decreasing order of their values.WhileICs(A)is the procedure that accepts a set of elements as input and sorts them according to the decreasing order of their values.ProcedureSh(A)schedules the elements on the virtual machines one by one.The virtual machine is selected to schedule an element characterized by the minimum value ofTvi.The procedure of each variant denoted byHGCP()is detailed in Algorithm 1.This procedure returns the solutionsandwithk={1,2,3}.The execution details ofHGCare given in Algorithm 2.The complexity of the algorithm isO(nlogn).

4.3 Mini-Load Half-Grouped Algorithm(MLH)

This algorithm is based on the grouping method.The two groups,G1andG2are constructed by the same method detailed in the above algorithm (Step 1 in Algorithm 3).The proposed algorithm uses three variants.For each variant,a solution is calculated,and the best solution is picked.In the first variant,there is any sort of changes to the setF.After creating the two groups,G1andG2,the scheduling of files will be based on the minimum load of the two groups.Let “a load of a group”is the sum of all file sizes in the group.So,initially,after constructing the two groups,the load ofG1denotes byLG1issfj,and the load ofG2denotes byLG2issfj.IfLG1≥LG2the first file inG1is selected and scheduled (Step 4 in Algorithm 3).Otherwise,the first file inG2is selected and scheduled(Step 7 in Algorithm 3)and soon on until all files are scheduled.The solution in this manner is calculated and denoted byGpV1(Step 11 in Algorithm 3).In the second variant,the files are sorted intoFaccording to the decreasing order of their sizes.The two groups are created and apply the minimum load to choose between groups.The solution in this manner is calculated and denoted byGpV2(Step 13 in Algorithm 3).In the second variant,the files are sorted intoFaccording to the increasing order of their sizes.Two groups are created and apply the minimum load to choose between groups.The solution in this manner is calculated and denoted byGpV3(Step 15 in Algorithm 3).Denotes byShF(G)the procedure that schedules the first file in the setG.The execution details ofMLHare given in Algorithm 3.The complexity of the algorithm isO(nlogn).

4.4 Excluding the Nv-Files Mini-Load Half-Grouped Algorithm(ENM)

This algorithm is based on the grouping method.Firstly,theNvbig files are excluded.TheseNvfiles denoted byLNVare scheduled on the virtual machines.Each file will be assigned to an available virtual machine.After that,for the remainingNf-Nvfiles denoted byRFV,theMLHalgorithm is adopted to schedule these remaining files to the virtual machines taking into consideration theNvfiles already scheduled.The complexity of the algorithm isO(nlogn).

4.5 One-by-One Half-Grouped Algorithm(OHG)

This algorithm is based on dividing the set of files into two groups following the same way described inHGC.Three variants are used.For each variant,a solution is calculated,and the best solution is picked.In the first variant,there is no sort of changes to the setF.After creatingG1andG2,two manners are applied to scheduling files.The first is to schedule the first file inG1after that,the first file inG2,until the scheduling of all files and the solutionGpV1is calculated.In a second manner,all files inG2are scheduled.After that,all files inG1are scheduled.The solutionGpV2is calculated.The Minimum betweenGpV1andGpV2constitutes the solution of the first variant.In the second variant,the files inFare sorted according to the decreasing order of their sizes.After creatingG1andG2,the two previous manners are applied to scheduling files.The solution is calculated for this second variant.In the third variant,the files inFare sorted according to the increasing order of their sizes.After creatingG1andG2,the two previous manners are applied to scheduling files.The solution is calculated for this third variant.The best of these three solutions is picked.TheOHGinstructions are given in Algorithm 5.The complexity of the algorithm isO(nlogn).

4.6 Swap Two-Files Half-Grouped Algorithm(STH)

This algorithm is based on dividing the set of files into two groups.Three variants are used.For each variant,a solution is calculated,and the best solution is picked.In the first variant,there is no sort of changes to the setF.The two groups are created in the same way described inHGC.After that,the first file inG1denotes byF1 is swapped with the first file inG2denotes byF2.The swap is to moveF1 to the first position inG2and to moveF2 to the last position inG1.The two manners described inHGCare applied to calculate the first solution.In the second variant,the files inFare sorted according to the decreasing order of their sizes.After creating the groups,G1andG2,the first file inG1is swapped with the first file inG2.Next,the two manners are applied,and the second solution is calculated.In the third variant,the files inFare sorted according to the increasing order of their sizes.The two groups are created in the same way described inHGC.After that,the first file inG1is swapped with the first file inG2.The two manners described inHGCare applied to calculate the third solution.The best of these three solutions is picked.The complexity of the algorithm isO(nlogn).

4.7 Swap One-in-Tenth-Files Half-Grouped Algorithm(SOH)

This algorithm is based on dividing the set of files into two groups.Three variants are used.For each variant,a solution is calculated,and the best solution is picked.In the first variant,there is no sort of changes to the setF.The two groups are created in the same way described inHGC.LetSt=After that,theStfirst files inG1is swapped with theStfirst files inG2.The swap is to move theStfirst files inG1to the front inG2and to move theStfirst files inG2to the last positions inG1.The two manners described inHGCare applied to calculate the first solution.In the second variant,the files inFare sorted according to the decreasing order of their sizes.After creating the groups,G1andG2,theStfirst files inG1is swapped with theStfirst files inG2.Next,the two manners are applied,and the second solution is calculated.In the third variant,the files inFare sorted according to the increasing order of their sizes.The two groups are created in the same way described inHGC.After that,theStfirst files inG1is swapped with theStfirst files inG2.the two manners described inHGCare applied to calculate the third solution.The best of these three solutions is picked.The procedureSWPT(G1,G2)swaps theStfiles as described above.The complexity of the algorithm isO(nlogn).In the experimental results,letHGSbe the algorithm that returns the minimum value after the execution ofHGCandSOH.In addition,letHMEbe the algorithm,which returns the minimum value after the execution ofHGC,MLH,ENM,OHG,andSTH.Finally,letHSSbe the algorithm,which returns the minimum value after the execution ofHGC,STH,andSOH.

5 Experimental Results

The discussion of experimental results is presented in this section.The proposed algorithms are coded in C++and compared between them to show the best algorithm among all.The computer used that executes all programs is an i5 processor and eight memories.The operating system installed in this later computer is Windows 10.the proposed algorithms are tested through four classes of instances.These classes are based on the normal distributionN[x,y] and the uniform distributionU[x,y][54].The different values of the file-sizesfjare given as follows:C1:U[15,150],C2:U[90,350],C3:N[250,30],andC4:N[350,90].For each pair ofNfandNvand each class,ten instances are generated.The values of theNfandNvare detailed in Table 3.In total,there 1240 instances.

Table 3: Size files and virtual machines values

The metrics used in[10]to measure the performance of the developed algorithms are:

•Fis theGpVvalue returned by the presented algorithm.

•Pcis the percentage of instances when

•APis the average ofGafor a group of instances.

•Timeis the average execution time.The symbol“+”is marked if the execution time is less than 0.001 s.The time is given in seconds.

Table 4 shows the overall results measuring the percentage,the average gap,and the time.In this latter table,the best algorithm isHME,with a percentage of 91.3%,an average gap of 0.042,and a running time of 0.001 s.The second-best algorithm isHSS,with a percentage of 81%,an average gap of 0.043,and a running time of 0.001 s.The algorithm that gives the minimum percentage of 33.4%isSOH.Table 4 shows that for all algorithms the average gap is less or equal to 0.001 s.The execution time is very close for all algorithms.

Table 4: Overall results measuring the percentage,the average gap,and the time

The load balancing applied on the cloud environment solving the studied problem is not integrally used in the literature.However,the load of files through several storage supports is treated in[10].The best algorithm developed in this latter work isSIDAr.After coding this algorithm and executing it over the instances used in this paper,a comparison with the best-proposed algorithmHMEresults in Table 5.This latter table shows thatHMEgives better results thanSIDArin 23.5% of cases with 292 instances.However,SIDArgives better results thanHMEin 29.3% of cases with 363 instances.Finally,there are 585 instances whenHMEandSIDArobtained the same results.To summarize,the best algorithm in[10]does not dominate the best-proposed algorithms.Consequently,a new algorithm can be developed based on the combination ofHMEandSIDAr.

Table 5: Comparison of the best-proposed algorithm with the best from the literature

Table 6 shows the average gap values when the number of files changes for all algorithms.There are only four cases when the average gap is less than 0.001.These cases are reached whenNf={10,25}for theHMEalgorithm andNf={400,600}forHSS.

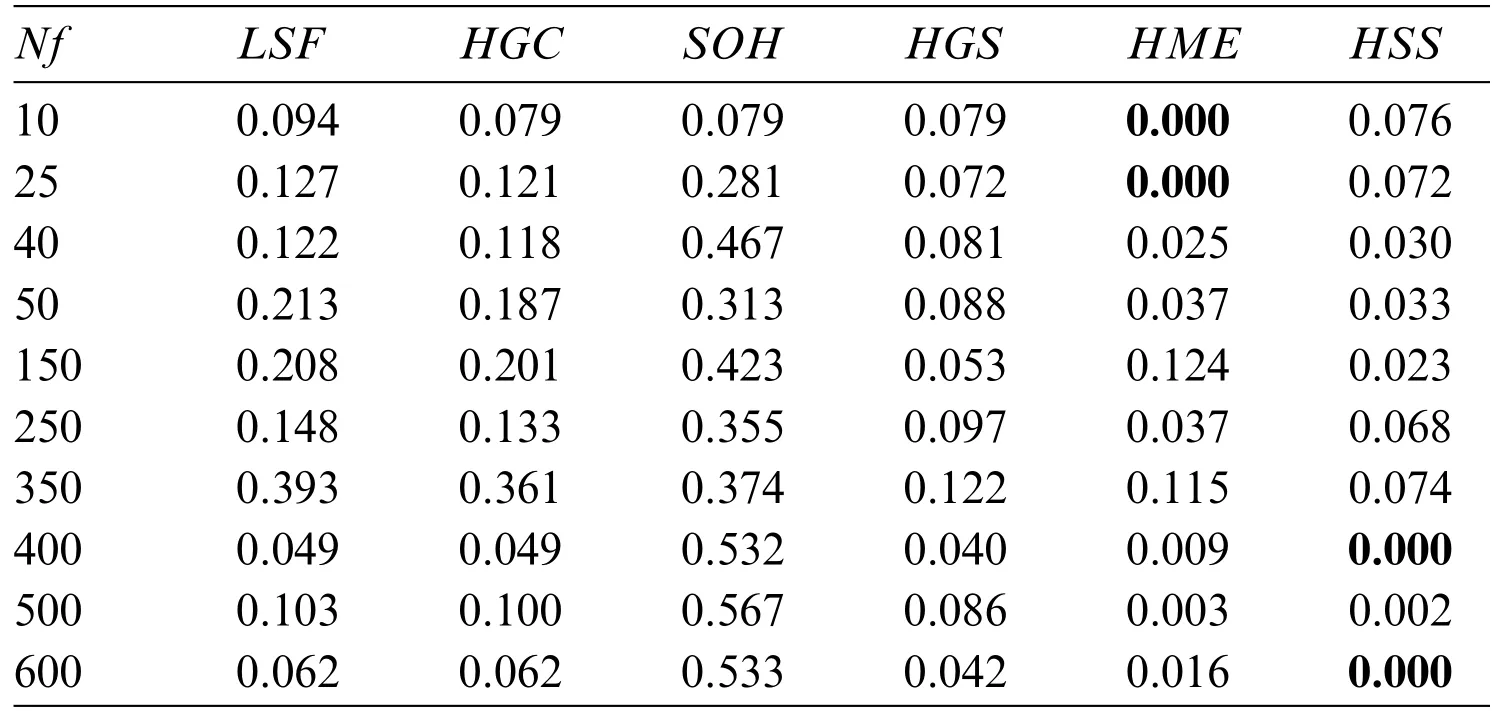
Table 6: The average gap criteria when the number of files changes for all algorithms

Table 7 shows the average gap criteria when the number of virtual machines changes for all algorithms.There are only two cases when the average gap is less than 0.001.These cases are reached whenNv={5,10}forHSS.The advantage to executeHMEis to reach a minimum average gap for almostNfvalues.The execution time ofHMEis polynomial.

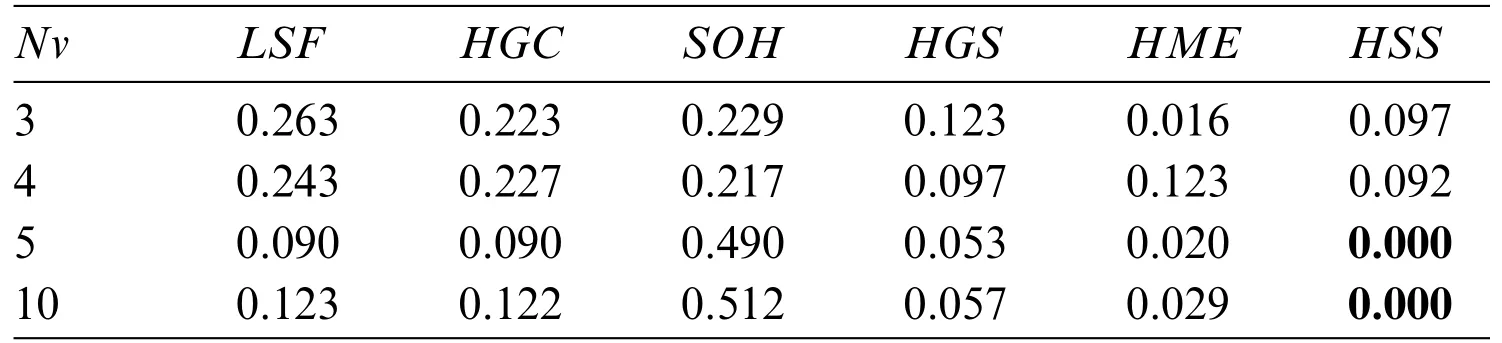
Table 7: The average gap criteria when the number of virtual machines changes for all algorithms

Table 8 presents the average gap criteria when the classes change for all algorithms.This table shows that forLSF,HGC,SOH,andHGSthe highest average gaps are observed for classes 3 and 4.This means that these classes are harder than classes 1 and 2 for these algorithms.However,forHME,the highest average gaps are observed for classes 1 and 2.This means that these classes are harder than classes 3 and 4 for this algorithm.Finally,forHSS,the highest average gaps are observed for classes 2 and 4.This means that these classes are harder than classes 1 and 3 for this algorithm.

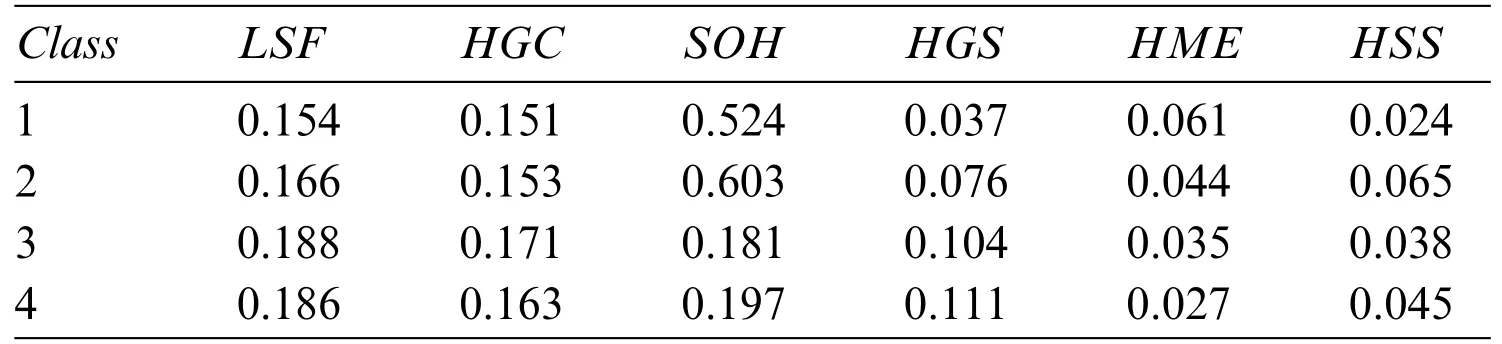
Table 8: The average gap criteria when the classes change for all algorithms

Fig.4 shows the average gap variation forSOHandHGSwhen the pair (Nf,Nv) changes.So,for each value(Nf,Nv),a pair value is given and presented in the figure with the related average gap.This figure shows that the curve ofHGSis always below the curve ofSOH.Indeed,the average gaps obtained bySOHare better than those obtained byHGS.

Fig.5 shows the average gap variation forHMEandHSSwhen the pair(Nf,Nv)changes.This figure shows that the curve ofHSSis 16 times below the curve ofHMEand 15 times the opposite.

Despite the performance of the proposed algorithms,a hard instance can be generated with bigscale ones.In addition,the studied problem does not take into consideration when the virtual machines do not have the same characteristics.Indeed,in the studied problem,we suppose that all virtual machines have the same characteristics.

Table 9 represents results comparisons with other state of the art studies.

Table 9: Results comparisons with other state of the art studies

Figure 5:The average gap variation for HME and HSS

6 Conclusion

In this paper,a new approach is proposed to schedule workflow in the cloud environment with utmost trust.Developed algorithms enable the scheduling process to choose the virtual machines that ensure load balancing.These algorithms provide more security to transferring workflow and minimize the time of data recovery in case of data loss.Our model is composed of three agents: the collector,

scheduler,and monitor.This model permits to visualization of the network links and node states permanently.The developed algorithms in the scheduler agent show promising results in terms of time and data protection.These algorithms are based on the grouping of several files into two groups.The choice of the file that is scheduled on the appropriate virtual machine is the most advantage of the work.Several iterative procedures are used in this paper.An experimental result is discussed using different metrics to show the performance of the proposed algorithms.In addition,four classes of instances are generated and tested.In total,there are 1240 instances in the experimental result.The experimental results show that the best algorithm isHME,with a percentage of 91.3%,an average gap of 0.042,and a running time of 0.001 s.The first line for future work is to enhance the proposed algorithms by applying several metaheuristics and considering the proposed algorithms as the initial solution.The second line is to propose a lower bound for the studied problem.The third line is to develop an exact solution and the last line is to develop intelligent algorithms for the monitor agent.After selecting the best algorithm,future research will focus on collector and monitor agents.The development of effective collection and monitoring agents enables the collection and analysis of meaningful information about virtual machines and intermediaries to decide on trusted bindings.

Acknowledgement:The authors extend their appreciation to the deputyship for Research&Innovation,Ministry of Education in Saudi Arabia.

Funding Statement:The authors extend their appreciation to the deputyship for Research &Innovation,Ministry of Education in Saudi Arabia for funding this research work through the Project Number(IFP-2022-34).

Author Contributions:Study conception and design:Mahdi Jemmali,Sarah Mustafa Eljack,Mohsen Denden;data collection: Mutasim Al Sadig;analysis and interpretation of results: Abdullah M.Algashami,Mahdi Jemmali,Sadok Turki,Mohsen Denden;draft manuscript preparation: Mahdi Jemmali,Sarah Mustafa Eljack.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:The data underlying this article are available in the article.All used materials are detailed in the experimental results section.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.