“认识角”的教学：从历史渊源中寻找启示

刘加霞 刘琳娜

【编者按】  数学史之于数学教育的价值已经取得共识。

近年来，北京教育学院刘加霞教授的团队在研读中外数学经典文献和数学史研究力作的基础上，聚焦小学数学的多个核心知识，深入挖掘与之密切相关的数学史料，适当选择数学史料融入教学的方式，开发了多个数学史融入数学教学（HPM）的课例。本期《专题研究》栏目聚焦“角”，依据数学史的梳理，对其教学展开探索。

摘 要： 小学数学中，“认识角”的核心内容是认识角的大小及其作用。

梳理《考工记》《几何原本》，发现：中国古代用规和矩作为基本工具进行几何操作，从而构建出一些特殊的角度，以满足技术规范的要求；古希腊数学则从360°分度体系的角度认识一般意义的角，将角度与圆弧对应起来，成为现代角的测量的本源。由此获得教学启示：突出直角的作用，体会度量单位产生的必要性；进一步感悟度量的本质——单位累加；用“长度”表示角的大小及其作用，有迹可循。

关键词：小学数学；数学史；角度；《考工记》；《几何原本》

一、引言

角是除了“点、线、面、体”之外的类似“原始概念”的一个概念，它既是一个图形，也是构成其他图形的基本要素。角的本质在于刻画直线的方向，因此，角的大小（角度）比角的定义更重要。

小学数学学习中，学生要分两次“认识角”，一般是在二年级和四年级。二年级主要是知道角的各部分名称，辨认角，知道直角、锐角与钝角，初步感悟“角的大小与角两条边的长度无关，是角两条边岔开的程度”；四年级主要是学习角的度量，知道平角与周角等。虽然两次“认识角”的深度不同，但是，核心内容都是认识角的大小及其作用，而非角的定义。

角的大小与长度、面积、体积等几何量有较大的差异。后三个量在本质上都是“单位的累加”。例如，作为最基本的几何量，（线段的）长度就是长度单位在同一方向上的顺次累加。因此，学生感知长度最为容易。但是，刻画角的大小有多种方法，角度单位的累加只是其中一种（没有量角器也可以刻画角的大小）。因此，学生认识角度要比学习其他几何量更有难度。教学中如何突破难点呢？

一门学科的历史是这门学科的教学指南，因为学生的理解具有历史相似性。早在19世纪，美国数学史家卡约黎就曾指出：“学生所遭遇的困难往往是相关学科的创建者经过长期思索和探讨后所克服的实际困难”，因此“数学史是数学教学的有效工具”。  ［1］ 由此，“认识角”的教学，可以通过追溯角度的发展史来突破难点。

中国古代和西方古代对角度概念和角度计量的建立有不同的發展路径。本文运用文献分析法对有关内容进行梳理，从中获得教学启示。

二、历史文献梳理

（一）《考工记》中特殊角度的表示方法及其运用

中国古代数学对角度的认识一直有欠圆满。  ［2］ 刘君灿曾断言：“中国除了直角之外没有一般的角度观念。”  ［3］ 关增建也曾指出：“中国传统计量中没有角度计量。”  ［4］ 角度在天文观测、农业生产、交通运输、文化娱乐、军事战争等领域有广泛的应用，如制造量器、农具、车辆、乐器、兵器等都涉及角度。没有角度的相关知识，中国古人是如何解决这些现实问题的呢？除了天文观测中涉及的角度问题（有学者认为，天文分度不是角度  ［5］ ）以外，古代技术百科全书《考工记》中有相关记载。《考工记》问世于两千多年前的春秋战国时期，据考是当时齐国的官书。它是我国最早的手工艺技术专著，重视“就事说事”，在解决不同领域问题时界定了各种特殊的角。

1.用“倨句”表示一般的角度

“在中国古代科技术语中，没有现代所用的角度这个词，古人利用‘倨句表示一般的角度概念。”  ［6］ 一般情况下，倨表示钝角，句表示锐角，倨句表示相应角度的大小。

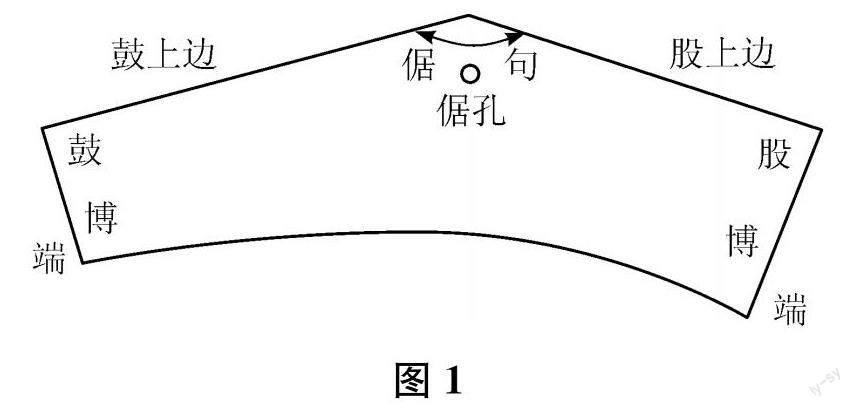
比如，《考工记·磬氏》中有：“磬氏为磬，倨句一矩有半。”这里的倨句指乐器磬（如图1所示）的“鼓上边”与“股上边”这两条边线的夹角，“一矩有半”是135°。

再如，《考工记·冶氏》中有：“戈广二寸，内倍之，胡三之，援四之，已倨则不入，已句则不 决…… 是故倨句外博，重三锊；戟广寸有半寸，内三之，胡四之，援五之，倨句中矩，与刺重三锊。”这段文字说明，兵器戈和戟的形制都与角度有关。具体来说，对于戈（如图2所示），要注意援和胡之间的角度关系：角度太钝，则不易啄入目标；角度太锐，则虽能创敌而不易割断之；二者间合适的角度应该是“倨句外博”，即比直角略大一些。对于戟（戈与矛的组合兵器），则要求“倨句中矩”，即援和胡纵横相交成直角。

2.“以矩生度”构造出以直角为基础的特殊角

中国古人对角度概念，首先是认识了一些特殊角。并且，中国古代技艺采取用特定的名称表示特定角度的方法，没有角度单位（如当下的1°角）的概念。具体来说，中国古人称“直角”为“矩”（矩本是画直角和方形的曲尺），以矩为基础角度，通过一些几何操作，进一步创生出其他角度概念。这样的方法称作“以矩生度”  ［7］ 。

比如，《考工记·车人之事》中有：“车人之事，半矩谓之宣，一宣有半谓之欘，一欘有半谓之柯，一柯有半谓之磬折。”若用现行分度法表示，这些角度的具体数值为：矩＝90°，宣＝ 1 2 ×90°＝45°，欘＝45°＋ 1 2 ×45°＝ 67°30′， 柯＝67°30′＋ 1 2 ×67°30′＝101°15′，磬折＝101°15′＋ 1 2 ×101°15′＝151°52′30″。用图形表示则如图3所示。矩、宣、欘、柯（在“车人为车”中柯也是长度单位，合今约60厘米  ［8］ ）、磬折就是一套特定条件下实用的角度单位制体系。《考工记》中，“韗人”制鼓、“车人”制耒、“匠人”兴修水利等都用到了“磬折”这个角度。因为“矩”是很容易得到的，所以这样的操作方法在实践中并不繁难。可见，中国古人就是在“具体问题具体分析”中摸索出解决实用角度问题的独特路径的。

需要注意的是，有文献认为，“磬氏为磬，倨句一矩有半”中磬的“鼓上边”与“股上边”的夹角就是磬折，因此，磬折的大小应该是“一矩有半”，即135°，但是，关增建认为，“磬氏制磬”中的倨句并没有明确地被称为磬折，因此，磬折的大小应该是“一柯有半”，即151°52′30″。  ［9］  史学界对于磬折到底是多少仍有争议，而对于倨句表示一般的角度概念则无争议。

3.“以规生度”构造出与周角相关的角度

“以矩生度”产生了宣、欘、柯与磬折，但是，仅有这几个特殊的角度，还不能满足生产生活需要，不能解决更多有关角度的现实问题。鉴于规和矩是古代最常用的几何工具，《考工记》中还采用了“以规生度”的方法来确定其他一些特殊角度。  ［10］

比如，《考工记·筑氏为削》中有：“筑氏为削，长尺博寸，合六而成规。”意思就是六把“削”（书刀）的刀背向外、依次排列而成一个圆（如图4所示）。由此，每把“削”的刀背弯曲成一个圆弧，其弧长是相应圆周长的六分之一，其所对的圆心角用现代360°分度系统来看就是60°。这里，实际上是用弧长刻画角度。

再如，《考工记·弓人》中有：“为天子之弓，合九而成规；为诸侯之弓，合七而成规；大夫之弓，合五而成规；士之弓，合三而成规。”这里，也都是用弧长表示角度。

《考工记》中记录的“以规生度”方法，可以看作弧度制的萌芽：虽然没有明确地用圆心角的度数表示角的大小，但是圆弧度量与角度度数表达在逻辑上是等价的。这种方法在描述星体的位置与运动方面有不可磨灭的价值。中国古代天文觀测中的盖天说、浑天说都是用圆弧长度刻画天体的位置，重在圆弧的线性度量。

总之，中国古代无论技艺器具还是天文观测中都没有发展出一般角的概念，重视的都是特殊角。由于中国古代数学中“矩”还指矩形，《周髀算经》《九章算术》中是用“隅”来称谓直角的，数学家们的注意力还是在“隅”这个特殊角上。《汉书·律历志》中有：“角，触也，物触地而出，戴芒角也。”这里，角虽然不再指兽角，但仍然表示尖锐的形状，而没有抽象为数学上的角。北宋沈括的《梦溪笔谈》中论及“隙出术”时所谈的角是方锥的顶角，即立体角。直到南宋杨辉的《详解九章算法》、明朝程大位的《算法统综》中所使用的“角”，才与现代角的含义基本上没有出入。中国古代数学著作中的角概念重在刻画边与边的交会空间，即重在图形角，研究角是为了研究几何图形，而不是抽象的角概念。 从技艺器具中的特殊角、天文观测中的圆弧度量到图形中的角，是角概念在中国古代发展的基本路线。中国古代几何中的“角”与天文中的“度”没有在“圆”中统一起来，是最大的遗憾。

（二）《几何原本》中对角度的界定及其对当下的影响

关于什么是“角”，西方几何学也有不同的观点，概述有三：角是两条直线方向的差别；角是从一边旋转到另一边的量；角是两条直线相夹的那部分平面。  ［11］

不同于中国古人“就事论事”地采用构造法解决角度测量的问题，早在古巴比伦时期，人们已经将圆周分为360度，每度分为60分，每分分为60秒。到了古希腊时期，人们已经有了清晰的角度概念，辅之以相应的测量仪器和测量方法，角度计量的建立也就水到渠成了。这一切，在古希腊数学名著《几何原本》中有完整的体现。

《几何原本》给出了角的一般定义，描述了角的分类、角的表示方法，以及如何对角进行比较。其中有关角度单位体系及角度单位的进位原则和具体测量方法的记录如下：

凡大小圆界，俱定为三百六十度，而一度定为六十分，一分定为六十秒，一秒定为六十微，一微定为六十纤。

夫圆界定为三百六十度者，取其数无奇零，便于布算。

凡有度之圆界，可度角分之大小。如甲乙丙角，欲求其度，则以有度之圆心置于乙角，察乙丙甲之相离可以容圆界之几度。如容九十度，即是甲乙丙直角；若过九十度者，为丁乙丙钝角；不足九十度者，为丙乙戊锐角。观此三角之度，其余可类推矣。

这里提到的“有度之圆界”就是现在学生学习角的度量必备的量角器，描绘的角度测量方法如图5所示。

需要说明的是，上面所引的内容出自清朝数学家梅珏成编纂的《数理精蕴》第二卷，来自意大利传教士利玛窦与明代学者徐光启合作编译的《几何原本》。由于所翻译的底本的差异，目前通行的汉语版《几何原本》（翻译的底本是西斯版，更符合《几何原本》的本意，而没有加入后人的解释）中并没有这些内容。

虽然利玛窦与徐光启合作编译的《几何原本》不能很好地体现《几何原本》的本意，尤其是不能凸显几何学的公理化思想，但是，他们把360°圆心角分度体系介绍到了中国。我们接受了360°圆心角分度体系，从而有了表示角度大小的单位划分，有了统一的单位制度就能进行测量，有了测量就能发展成为计量。当然，要建立真正的角度计量，还必须建立相应的角度基准（如检定角度块）和测量仪器，但是无论如何，没有统一的单位制度，就不可能建立角度计量，因此可以说，《几何原本》的引入为中国角度计量的出现奠定了基础。

综上，中国古代在没有角度定义和单位体系的情况下用规和矩作为基本工具进行几何操作，从而构建出一些特殊的角度，以满足技术规范的要求，重在解决实际问题。古希腊数学则从360°分度体系的角度认识一般意义的角，将角度与圆弧对应起来，成为现代角的测量的本源，重视通过公理化思想建构几何知识体系。中国古代数学关注“实用性”（当然，刘徽除外）与古希腊数学重视逻辑推理（强调理性精神）形成了鲜明的对比。

三、教学启示

通过有关角度的历史文献梳理，可得如下启示：认识事物可以从特殊到一般，小学生认识角可以从特殊的角度入手，感悟直角无处不在，再认识锐角、钝角等，然后进一步认识构成角的要素，辨别、描述一般的角。教学中，可以探究前述古代先民们创造的工具中的角度，了解这些特殊角的名称以及各个角之间的大小关系，感悟角也可以“分割、累加”，为用量角器测量角积累度量经验，并感悟悠久灿烂的中华传统文化。具体来说，二年级和四年级“认识角”的教学要重视以下内容：

第一，突出直角的作用，体会度量单位产生的必要性。在以往的教学中，为帮助学生认识角的度量单位，通常会让学生多次进行“用小角量大角”的活动，经历度量单位产生的过程，感悟统一度量单位的必要性。通过史料梳理，发现《考工记》中的角度大多以“矩”为源，而“矩”也是学生最常见的图形或角度。教学中，要以此为“切入点”和“主线”，贯穿角的分类、角的度量全过程。

第二，进一步感悟度量的本质——单位

累加。与以往学习的有关度量的知识联系起来，认识到角的度量不是一个孤立的知识模块，而与长度度量、面积度量具有内在的一致性——度量單位累加，当然也有不同——角的单位累加更复杂。教学中，不要急于让学生进行没有思维含量的“量角”活动（如机械记忆“二合一看”），而要重视“要量的角”如何与“量角器上的角”重合，如何读出量角器上角的度数，即重视“角的单位”是按顺时针还是逆时针依次累加的。

第三，用“长度”表示角的大小，有迹可循。古人在“以规生度”的过程中是用“弧长”表示“角度”的。基于历史相似性，学生用“长度”表示角的大小似乎很自然。课堂上隐约有很多学生是用“长度”表示角的大小的：当角的两条边长度固定时，用两条边另一端点连线的长度表示角的大小。教学中，不要忽视学生的一些思维生长点，而要撬开一个小口，鼓励学生基于学习兴趣深入研究，也为中学学习三角函数积累经验。

参考文献：

［1］ 汪晓勤.HPM视角下的小学数学教学［J］.小学数学教师，2017（7/8）：77 83+2.

［2］［11］ 李迪.数学史研究文集（第二辑）［M］.呼和浩特：内蒙古大学出版社，1991：6，6.

［3］ 刘君灿.影响中国传统数学发展的动因探索［J］.淡江史学，1990（2）：61 71.

［4］ 关增建.传教士对中国计量的贡献［J］.自然科学史研究，2003（增刊1）：33 46.

［5］［6］［7］［9］［10］ 关增建.中国古代角度概念与角度计量的建立［J］.上海交通大学学报（哲学社会科学版），2015（3）：52 59，52 59，   52 59 ，52 59，52 59.

［8］ 陈睿锋.《考工记》中初见端倪的原始角度计量技术［J］.中国计量，2015（6）：63 64.