用于批产卫星的稀疏红外灯阵空间热流模拟方法

姜 峰，孔 林，王建超，王殿君，柏 添

（长光卫星技术股份有限公司，长春 130033）

0 引言

卫星热平衡试验中常见的外热流模拟方法主要有红外加热笼、热辐射板和红外灯阵模拟[1]。外热流模拟的偏差直接影响卫星内各部件的温度水平。红外加热笼一直是空间外热流模拟最常用的手段。由于其是定制化的产品，对任何外观形状的卫星均能够根据热流模拟需求调整功率和加热带之间距离，所以能够同时保证卫星在轨高温和低温工况下的热流需求；但是其结构设计较为繁琐，制造成本较高，加工周期长，尺寸空间大，难以满足批产卫星的热流模拟需求[2]。用于模拟外热流的辐射板一般要求材料密度小、导热性能好以及可加工性强，因此常用染黑铝板，其模拟稳态热流均匀程度十分出色；但铝板厚度的增加会增强其热惯性，使瞬态热流模拟有一定偏差，而且辐射板对星体遮挡较强，难以保证低温工况的热流水平[3]。

本文在研究红外灯管功率特性、辐射特性及热流分布规律的基础上，提出针对批产卫星的稀疏红外灯阵热流模拟方法，要求热流不均匀度引起的卫星舱板温度最大值与最小值的差值（温度梯度）＜3℃、稀疏红外灯阵覆盖系数（灯阵总面积与被模拟表面的比值）＜5%、卫星热流模拟偏差＜3%。通过采用稀疏红外灯阵热流模拟方法，仅简单调整灯阵布局及位置就可重复用于不同型号批产卫星的热流模拟，从而提升热试验效率，满足卫星批量化的研制要求。

1 红外灯管特性

1.1 红外灯管选用及组成

图1 红外灯管尺寸Fig.1 Dimension of infrared lamp tube

1.2 红外灯管的伏安特性

每只红外灯的伏安特性会因灯管的制造工艺而略有差异，因此首先对红外灯的伏安特性进行测量，采用控制变量的方法，记录不同电流下的电压值[4]。实际测量值与理论计算值对比如图2 所示，可见，二者有一定差异。

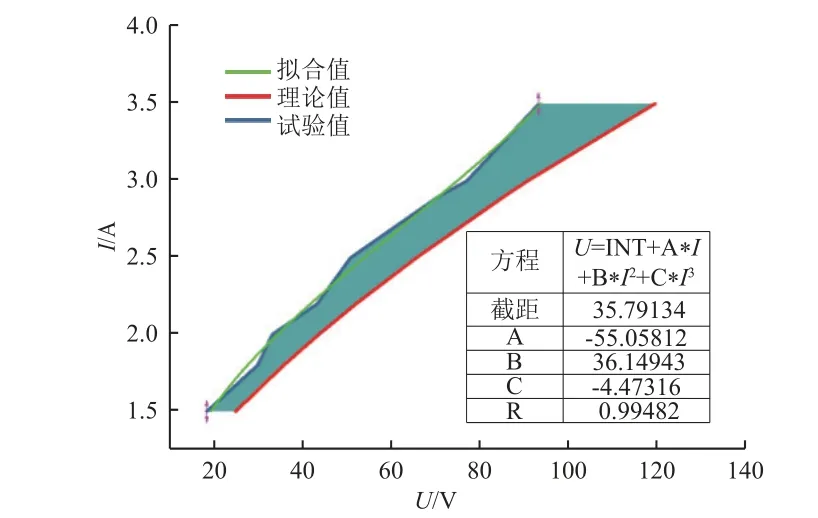
图2 红外灯管伏安特性Fig.2 Volt-ampere characteristics of infrared lamp tubes

灯管电压于电流测量值的拟合曲线表达式为

由式(1)得到的拟合结果与实际测量值之间相关性达到了0.99。通过式(1)计算灯管的电流与电压值，设定电源电流与电压以满足试验过程灯管功率输出需求。

1.3 红外灯的辐射特性

红外灯的光谱分布与灯丝的温度直接相关，而灯丝的温度取决于红外灯的功率，因此研究红外灯的功率特性是研究红外灯光谱分布的前提条件。

取灯丝的长度为150 mm、直径为1 mm，同时考虑到红外灯灯内钨丝的样式，则当达到热平衡时灯丝温度T可以按圆柱体发热计算，即

式中：P为灯丝功率；ε为灯丝发射率，此处取值为0.85；S为灯丝有效辐射面积，m2；σ为斯忒藩-玻耳兹曼常量，5.67×10-8W/(m2·K4)。根据式(2)计算出灯丝温度为2137 ℃。

灯丝发出的粒子到达石英灯管后可能被反射、透射或者吸收，因此将灯管视为灰体，不考虑辐射特性与频谱关系，红外灯管等效发射率取值为0.2，等效透射率取值0.8，在真空热试验中当达到热平衡时，石英玻璃的温度TD为[5]

式中：qD为灯管发热功率；η为石英灯管吸收热量比，η=1～0.8；由于灯管具有很强的透射性，灯管吸收灯丝热量后可通过内外表面向空间辐射，故SD为石英玻璃管内外表面积之和； εD为石英灯管的发射率。计算得出石英玻璃温度为713 ℃，后续对其进行仿真验证。

2 红外灯管热流分布研究

2.1 数值建模方法

根据上述红外灯管的尺寸及辐射特性等参数建立仿真模型如图3 所示，其中忽略了支架及安装孔等对结果影响较小的特征，灯管采用壳单元，灯丝采用实体网格。

坐在父母身边，父亲对母亲说：“你看老三这头发多好，油黑油黑的。”我冲二老一笑：“你们的老花眼哪能看到我冒出的白头发。”饭桌上，母亲一头白发，父亲一头稀发，我一头黑发，凑到一起大笑起来。墙上的老相框里，头发乌黑浓密的父亲、编着麻花长辫的母亲，一直面露他俩结婚时的喜悦笑容瞧着这个家，瞧了五十多年。

图3 红外灯管仿真模型Fig.3 Simulation model of infrared lamp tube

仿真结果如图4 所示，灯丝平衡温度为2175 ℃，石英玻璃平衡温度为750 ℃，环境温度-60 ℃，灯管发射功率500 W。仿真结果与解析计算结果基本一致，说明数值仿真模型可用于热流模型仿真计算。

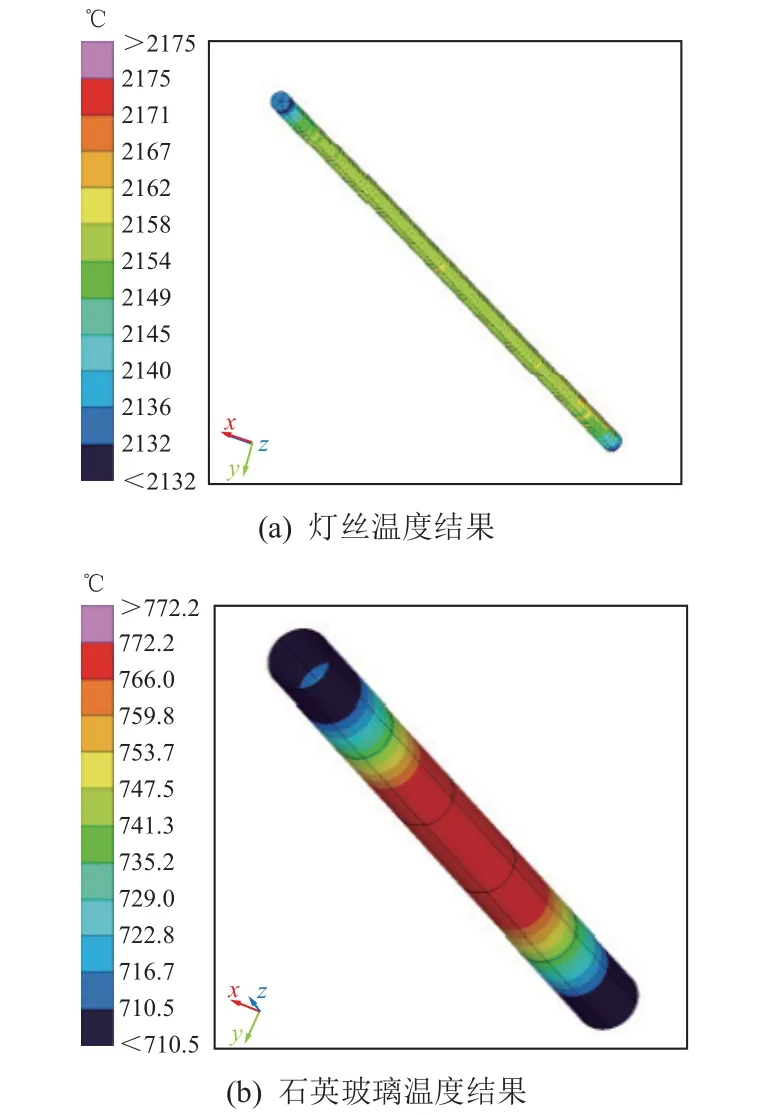
图4 红外灯管温度计算结果Fig.4 Temperature calculation results of infrared lamp tubes

2.2 单灯热流分布计算

红外灯管与被加热表面的距离直接影响热流的均匀程度：距离越远，热流均匀性越好，但有效热流越小；反之，距离越近，热流越不均匀，但有效热流越大[6-7]。考虑到真空容器的实际尺寸，为了便于后期试验验证，本文研究辐射距离为300 mm 的热流分布情况。

对单灯热流分布特性进行有限元仿真计算，环境温度为-60 ℃。建立500 mm×500 mm 铝板，其背部包覆多层隔热组件，其上均匀分布21 个热流计；灯管为水平状态，其中心位于垂直铝板平面且距铝板中心点300 mm 处。灯管与热流计布置如图5 所示，其中：Q1～Q21 为热流计编号；铝板平面中心为原点，x向为铝板平面内平行于灯管轴向，y向为铝板平面内垂直于灯管轴向。采用蒙特卡罗法计算得到的热流分布如图6 所示，可见：位于铝板中心的Q1 的热流为300 W/m2，在距离中心150 mm 的位置，即Q2～Q5，其热流平均值为206 W/m2；在距离中心210 mm×210 mm 的位置，即Q6～Q9，其热流平均值为155 W/m2；在距离中心250 mm 的位置，即Q10、Q11、Q16 和Q17，其热流平均值为139 W/m2；在距离中心350 mm 的位置，即Q18～Q21，其热流平均值为84 W/m2。

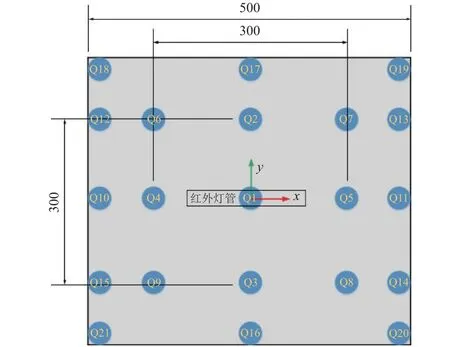
图5 热流计分布Fig.5 Layout of heat flow meters

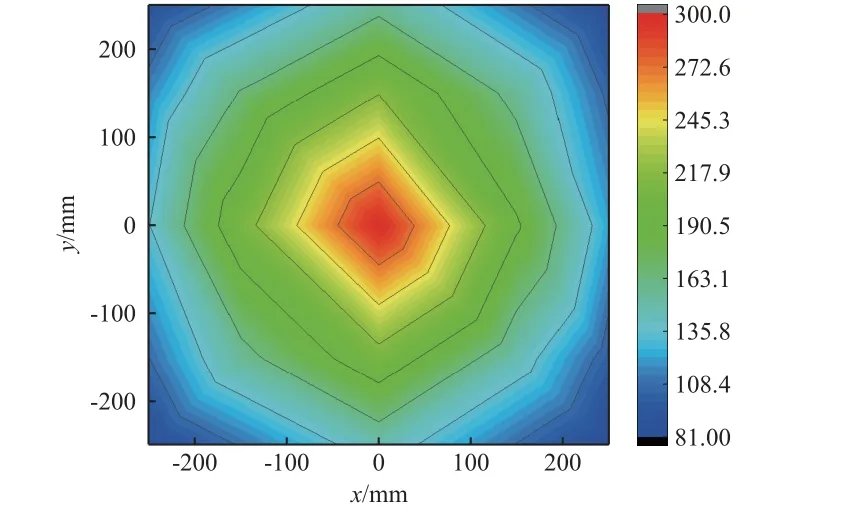
图6 单灯热流分布数值计算结果Fig.6 Numerical calculation results of single lamp heat flux distribution

2.3 热流分布试验测试

为了验证单灯热流分布的仿真结果与实际结果的吻合程度，采用与有限元仿真相同的设定条件开展单灯热流分布试验。试验状态如图7 所示。试验在真空度为6.65×10-3Pa、热沉温度为-60 ℃条件下进行；热流计采用带有补偿铜片式绝热型热流计，用以抵消安装板的热流影响[7-10]，其分布如图5所示。

图7 红外灯单灯热流分布测试试验Fig.7 Heat flux distribution test of a single infrared lamp

单灯热流分布试验测量结果如表1 所示。与仿真结果对比可知：距离铝板中心250 mm 以内，试验结果与仿真值的差异在10%以内。因此认为热流分布数值仿真计算方法可行。

表1 热流分布结果统计Table 1 Statistics of heat flux distributions

根据红外灯距离加热平面300 mm 的热流试验测试结果，拟合出热流分布计算公式为

式中：x和y分别为沿x轴和y轴（见图5）距中心点的距离；q1为铝板中心（Q1）的热流值，为298 W/m2。根据式(4)的计算结果绘制的热流分布规律如图8所示，可见：热流呈中心对称分布，中心热流值最大，且随到中心的距离的增大而减小。

3 红外灯管控制逻辑优化

灯阵热流控制的试验结果如表2 所示，可见：热流计温度与环境温度差异越大，热流的波动程度越大，同时所测量的热流平均值与设定值之间的偏差也就越大，分别为-1.02 W/m2、-3 W/m2、-4 W/m2、-7 W/m2。因此，要实现更高精密热流输出，就需要对现有控制逻辑进行优化设计。

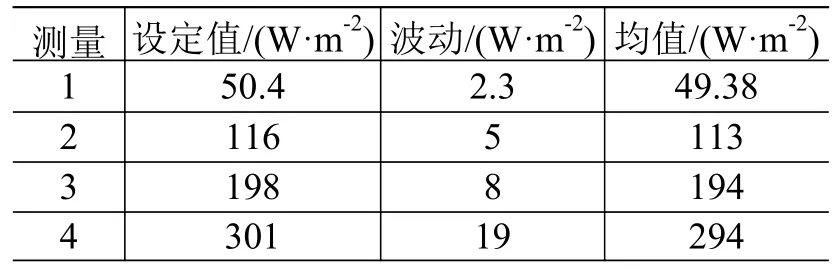
表2 红外灯阵不同热流输出控制结果Table 2 Differenct heat flux output control results of infrared lamp array

控温逻辑分为比例控温和门限控温两种方式。比例控温方式是按照当前温度在控温门限的区间将额定功率进行比例控制。门限控温是设置控温区间，低于区间温度下限以满功率对被控对象加热，高于区间温度上限则关闭电源输出。由于红外灯的阻值随输出功率变化，所以两种控温方式下结果均有一定偏差。为对比不同控温方式的效果，设计热流控制方案如表3 所示，其中：热流控制目标值设定为300 W/m2；方案1 为常用热流控温方式，因此设置其为对照组。

表3 红外灯阵热流控制方案Table 3 Heat flux control scheme of infrared lamp array

各方案下的热流控制结果与目标值的对比如图9 所示，可见：1）方案1 的热流波动最大，达到21 W/m2；2）当减小门限控温区间，与方案1 的结果相比，方案2 的热流波动降低了4 W/m2，方案3 的降低了5 W/m2，此时热流波动已经无法有效减小；3）方案4 已经将热流波动缩小至11 W/m2，但由于此时热流相较目标值偏低，所以将热流计控温上限继续上调，即方案5 的25 ℃和方案6 的30 ℃，此时热流波动均降低为3 W/m2；4）方案7 在方案5 的基础上调节了控温下限，热流控温精度进一步提高，为最优方案。

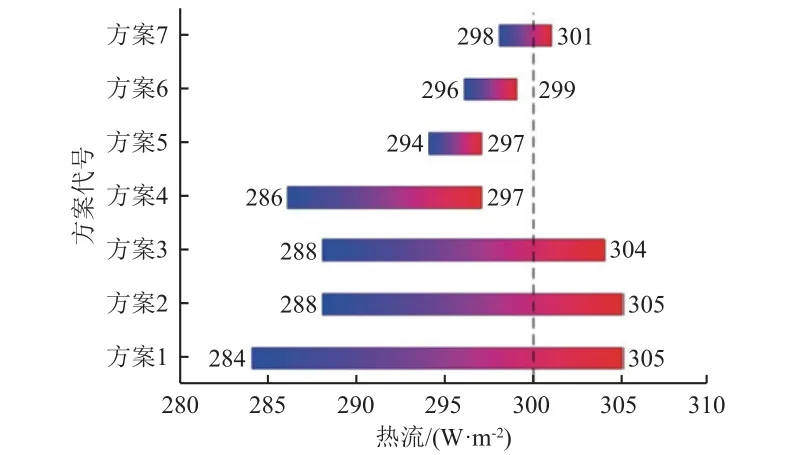
图9 不同方案热流控制结果Fig.9 Heat flux control results of different schemes

不同方案的热流控制结果表明：1）门限控温方式不适用红外灯阵的热流模拟；2）由于比例控温是针对不同温度区间按不同比例调制加热功率，所以增大控温上下限能够让温度波动更为稳定；3）比例控温方式下设置合适的比例控温区间能够实现外热流的精确模拟，例如方案7，将趋势控温的下限设定在较目标温度低1 ℃以内，同时将控温上限调至高于下限5 ℃以上，可以实现热流控制精度≤3 W/m2。

4 稀疏红外灯阵热流模拟方法

4.1 红外灯阵优化前

以热流不均匀度最小为目标，对500 mm×500 mm 的卫星铝板表面热流模拟展开研究。依据红外灯管热流分布规律，灯阵与加热表面的垂直距离选定300 mm，设计灯管数量及分布。热流分布不均匀度为[11-14]

式中qmax和qmin分别为最大和最小热流值。

选用10 根灯管，如图10 所示对称分布，其轴向为x向、垂直轴向为y向；灯管x向间距为200 mm、y向间距为160 mm。

图10 红外灯阵位置分布图Fig.10 Layout of infrared lamp arrays

铝板表面热流分布结果如图11(a)所示，可见其最大热流为306 W/m2，最小热流为278 W/m2；按式(5)计算的热流不均匀度ρ＜5%。卫星表面铝板温度分布如图11(b)所示，可见其温度梯度≤1 ℃。

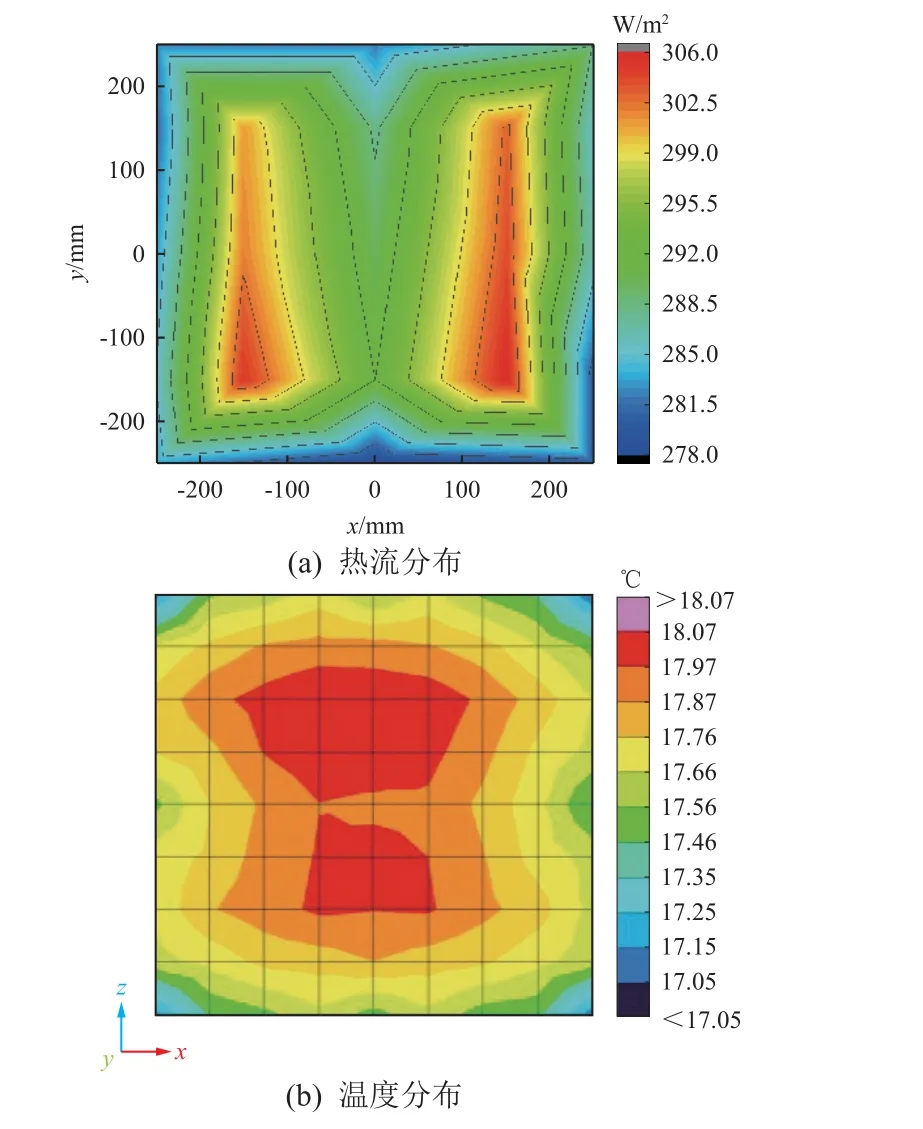
图11 均匀热流模拟下铝板表面热流分布和温度分布Fig.11 Distributions of heat flux and temperature of aluminum plate in uniform heat flux simulation

4.2 红外灯阵优化后

为了提高批产卫星试验效率，采用尽可能少的灯管实现热流等效模拟，本文提出稀疏红外灯阵热流等效模拟方法，即：不再以热流均匀性为目标，而是以卫星表面吸收的热量为目标来实现对卫星与环境间换热量的准确模拟。

同样以500 mm×500 mm 的卫星表面铝板为例，结合热流分布规律研究结果，对灯阵进行设计优化，其分布如图12 所示，仅采用4 根红外灯管，其x向间距为230 mm、y向间距为450 mm；通过比例控制方法（方案7）调节红外灯管功率，在保证铝板温度梯度＜3 ℃的情况下，同时对表面热流进行积分，使铝板表面吸收的总热量与设计值的偏差在5%以内。试验结果如图13 所示，可见，铝板表面热流不均匀度为9%、温度梯度为1.22 ℃。此时铝板表面吸收的总热量为63 W，与设计值相差1 W，热流模拟偏差为1.5%，对卫星温度影响很小，因此认为稀疏红外灯阵热流模拟方法可行。

图12 稀疏灯阵分布Fig.12 Layout of sparse lamp arrays

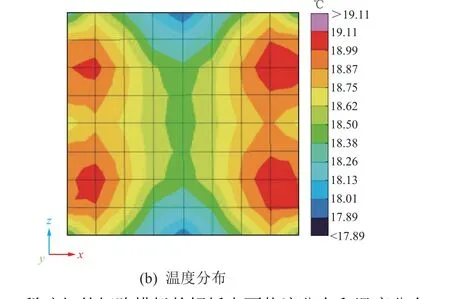
图13 稀疏红外灯阵模拟的铝板表面热流分布和温度分布Fig.13 Distributions of heat flux and temperature of aluminum plate in sparse infrared lamp array simulation test

5 结束语

本文针对批产卫星的红外灯空间热流模拟需求，开展了稀疏红外灯阵热流模拟方法研究。首先分析了红外灯管辐射特性以及功率特性，并进行了数值建模与仿真分析；然后试验测试了红外灯的伏安特性和热流分布特性，结果验证了数值建模与仿真计算方法是准确可靠的；继而对红外灯管控温逻辑进行研究，结果表明选取比例控温方式并且通过向温度上限拉偏控温门限能够保证红外灯阵热流控制精度与稳定性＜3 W/m2；最后提出优化的稀疏红外灯阵热流模拟方法，对表面热流分布积分计算结果表明，可以控制被模拟表面吸收总热量偏差＜3%、温度梯度＜3 ℃；分析结果显示表面热流不均匀度为9%的情况下，温度梯度为1.22 ℃，热流模拟偏差1.5%，说明稀疏红外灯阵热流模拟方法合理可行。