环形桁架式空间薄膜展开机构运动精度可靠性建模与分析

尹大勇，胡 明，孟少华，高 云，吴 梅

（1.北京卫星环境工程研究所，北京 100094； 2.浙江理工大学 机械工程学院，杭州 310018）

0 引言

空间薄膜展开机构是薄膜天线、太阳帆及太阳电池阵的重要组成部分。作为薄膜索网的支撑结构，环形桁架式空间薄膜展开机构主要由杆件构成，其展开到位后的姿态和位置精度会对薄膜索网的工作形态产生影响。加工装配误差、连接间隙及服役环境扰动等因素均可能导致机构展开运动存在误差，从而偏离预定姿态和/或位置[1]，这就是展开机构的运动精度可靠性问题。机构的运动精度可靠度是指机构最终的运动姿态和位置输出相较理想情况下的运动姿态和位置输出的偏差值在期望误差指标范围内的概率。研究环形桁架式空间薄膜展开机构的运动精度可靠性，对确保展开机构实现在轨功能和性能具有重要意义。

国内外对于空间展开机构可靠性已有诸多研究，如：Castet 等利用威布尔拟合和非参数分析对卫星及其子系统的可靠性进行了建模分析[2]；Hogstrom等对三棱柱形空间薄膜展开单元进行了运动精度可靠性仿真[3]；Jawale 等研究了杆件尺寸公差影响下四杆机构的运动精度[4]；Wang 等针对关节铰链间隙对运动精度的影响，提出了一种混合降维方法（HDRM），提高了仿真计算的效率[5]；Choi 等利用蒙特卡罗方法研究了制造公差和关节间隙不确定的机械手运动可靠性[6]；Ting 等针对关节间隙提出了N 杆机构末端运动精度量化模型，适用于包含旋转和棱柱形关节的单环连杆机构[7]；刘珺蕙应用非概率模型对星载薄膜天线展开可靠性进行了分析，并给出了求解方法[8]；陈建军等利用区间概率分析方法对星载展开天线结构在不同工作阶段的可靠性进行了研究[9]；靳宁将贝叶斯网络方法引入某星载薄膜天线展开系统多状态可靠性分析，得到了多种失效事件概率的计算方法[10]；高静丽采用模糊动态贝叶斯方法对天线展开系统进行了模糊可靠性建模与分析[11]；张建国等对周边桁架式星载薄膜天线建立了非概率运动精度可靠性模型，推导出了考虑尺寸误差及空间因素的非概率可靠性计算公式[12]；胡明等结合ADAMS 及Monte Carlo 方法对空间折叠展开机构运动精度可靠性进行了仿真分析，并求解了可靠度[13]。上述研究为空间薄膜展开机构运动精度可靠性建模与仿真提供了较好的基础。目前如何兼顾运动精度可靠性的精确建模及高效仿真是展开机构可靠性研究领域的热点问题。

本文以环形桁架式空间薄膜展开机构为对象，建立其运动精度可靠性理论模型，利用ADAMS/Insight 模块进行基于杆长误差的展开机构运动精度可靠性仿真，并求解其运动精度可靠度，从可靠性角度为环形桁架式空间薄膜展开机构的优化设计提供依据。

1 展开机构简介

空间薄膜展开机构中，环形桁架是最具大尺寸、轻质化发展潜力的结构之一，其主要由驱动部件、同步展开机构、缓释装置和锁定装置组成。该机构除可以实现正常的折展功能之外，还需满足以下要求：1）为保证折展动作的确定性，折展单元自由度应为F=1；2）无源驱动，通过缓释装置实现平稳展开动作，展开时间应在90 s 以内；3）运动副应避免使用复杂连接副，一般以平面低副为主，通常采用铰链连接。

环形桁架式空间薄膜展开机构折展单元构型如图1 所示，其中：展开杆4 个，分别为AB、AF、CD和DE；支撑杆4 个，分别为AS、LR、DS和QT；其余为活动杆件共13 个，转动副19 个。若以折展单元中杆AD为机架，则其折展单元自由度为

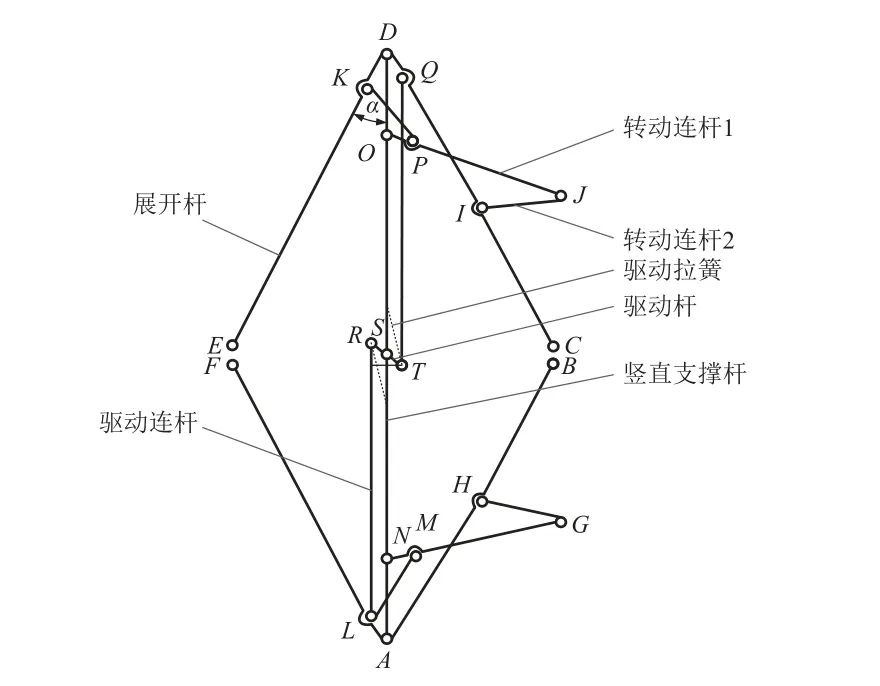
图1 环形桁架式空间薄膜展开机构折展单元构型Fig.1 Configuration of folding unit of the annular truss space membrane deployable mechanism

式中：N为活动杆件数；G为转动副数目。

为保证环形桁架式空间薄膜展开机构折叠展开运动过程的协调性，折展单元一般采用正多边形轮廓。本文所研究对象为由8 个折展单元构成的展开机构（如图2 所示），其采用模块化设计且每个折展单元以弹簧驱动展开，利用电机驱动绳索来约束弹簧驱动，以实现展开机构展开过程的平稳可控。

图2 环形桁架式空间薄膜展开机构的构型Fig.2 Configuration of the annular truss space membrane deployable mechanism

2 展开机构运动精度可靠性理论建模

作为空间天线的支撑结构，环形桁架式空间薄膜展开机构的展开到位精度决定了薄膜索网的工作形态。以展开到位时8 个竖直支撑杆支撑点的展开位置所拟合的空间圆心坐标位置（见图3）及半径误差作为特征参量，建立展开机构的运动精度可靠性模型。

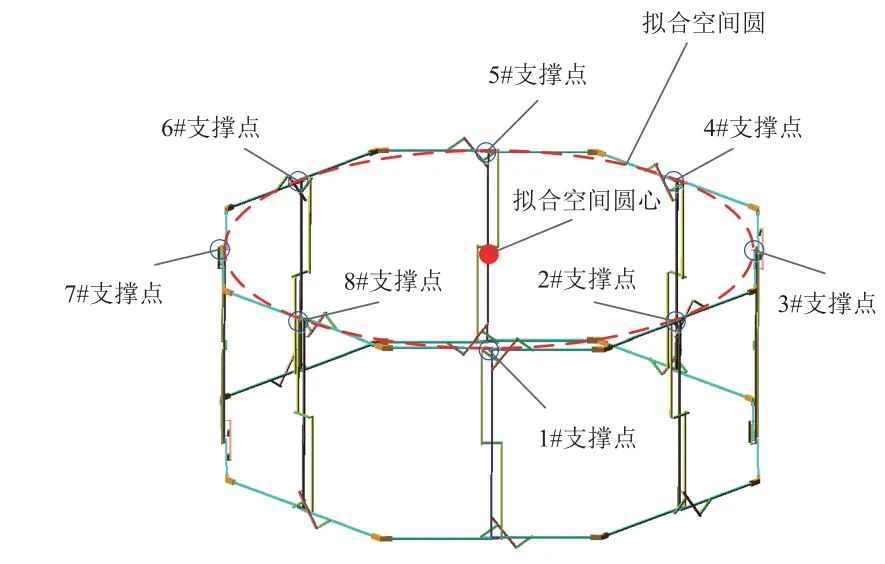
图3 环形桁架式空间薄膜展开机构展开到位状态下支撑点拟合空间圆示意Fig.3 Schematic of the spatial circle fitted by the supporting points of the fully deployed annular truss space membrane deployable mechanism

假设空间圆的圆心坐标(xc,yc,zc)在三个方向的位置误差允许值为[Δx, Δy, Δz]，半径误差允许值为Δr；若展开到位时空间圆圆心三个方向上的位置误差和半径误差均在允许范围内，即

则认为可展开机构展开可靠。式(2)中Δr为8 个支撑点的半径误差均值。

以图1 中1#单元支撑杆下端点A作为展开机构的全局坐标系原点O1，支撑杆AD作为z轴。根据右手定则分别确定x、y轴方向并建立全局坐标系O1x1y1z1，按逆时针方向对其余单元建立局部坐标系Oixiyizi，保证每个相邻单元的局部坐标系间夹角均为β。

设杆件AL、MN、DK和DQ的长度lAL=lMN=lDK=lDQ=50 mm，则 各 支 撑 杆 上 端 点Di的 坐 标(xDi,yDi,zDi)为

式中，lAB、lTQ和lRT分别为杆件AB、TQ和RT的长度。

假设展开杆lAB的展开角度为α，则输出运动参数矢量Ui=[xDi,yDi,zDi]T，输入运动参数矢量V=[α]。若每个折展单元的4 根展开杆的展开输入运动相同，则输入运动参数矢量V=[α]，结构参数矢量L=[lAB,lTQ,lRT]T，那么点Di的坐标(xDi,yDi,zDi)的表达式分别为：

由于各支撑点的位置误差计算方法相同，故选择支撑点D2(xD2,yD2,zD2)进行分析。利用一阶泰勒展开，点D2的位置误差表达式为

式中：u、v和w为空间圆所在平面参数，即ux+vy+wz- 1 = 0。

式(9)为超定方程组，进行最小二乘法求解得

将8 个离散点坐标分别代入式(11)，得

简化后为

由于圆心必须在拟合圆所在平面，所以满足

假设环形桁架式空间薄膜展开机构展开到位后，8 个支撑点所拟合的空间圆圆心坐标及圆半径满足正态分布，则x向的位置可靠度为

同理，替换成Δyc、Δzc和r，可求得相应的可靠度，得到拟合空间圆的圆心坐标及半径。

据此，环形桁架式空间薄膜展开机构的运动精度可靠性理论模型为

式中：Rxc、Ryc、Rzc分别为可展开机构拟合空间圆的圆心位置在x、y、z向的可靠度；Rr为可展开机构拟合空间圆半径尺寸的可靠度。

3 展开机构运动精度可靠性仿真分析

3.1 参数化仿真模型建立

基于ADAMS 仿真平台，建立环形桁架式空间薄膜展开机构的参数化模型。通过ADAMS/Insight模块进行机构的运动精度可靠性仿真[14]。结合运动精度可靠性模型、蒙特卡罗法及MATLAB 对仿真结果进行处理[15-16]，求解环形桁架式空间薄膜展开机构展开到位后各单元支撑点的空间坐标。

利用SolidWorks 对环形桁架式空间薄膜展开机构进行三维建模，确定机构的关键点位置，创建设计点及几何体模型，获取关键点坐标。由于环形桁架式空间薄膜展开机构主要由连杆铰接而成，所以在ADAMS 中可将关键点坐标参数化并创建设计点，同时将连杆与关键点关联，即在修改关键点位置时，连杆的尺寸会相应改变。

根据环形桁架式空间薄膜展开机构的运动精度可靠性理论模型，在参数化模型中选取图1 中杆件RT、AB和TQ的杆长作为设计变量（如表1 所示）；结合加工精度要求，选择加工公差等级为IT5。

表1 杆长设计变量Table 1 Rod length design variables

根据环形桁架式空间薄膜展开机构的折展单元各连接杆件关系，将上述设计变量代入式(4)、式(5)和式(6)，实现杆件尺寸的参数化。1 个单元中杆件端点参数化坐标见表2。当设计变量发生变化时，端点坐标也会随之变化，从而实现杆件尺寸的自动修改。

表2 杆件端点参数化坐标Table 2 Parameterized coordinates of the rod end points

将环形桁架式空间薄膜展开机构的8 个单元添加转动副，驱动（角速度）函数为STEP(time, 0,0d, 11.25, 1.0332d ) +STEP(time, 67.5, 0d , 78.75,-0.5166d )+STEP(time, 78.75, 0d , 90, 0d )，驱动函数仿真曲线如图4 所示。

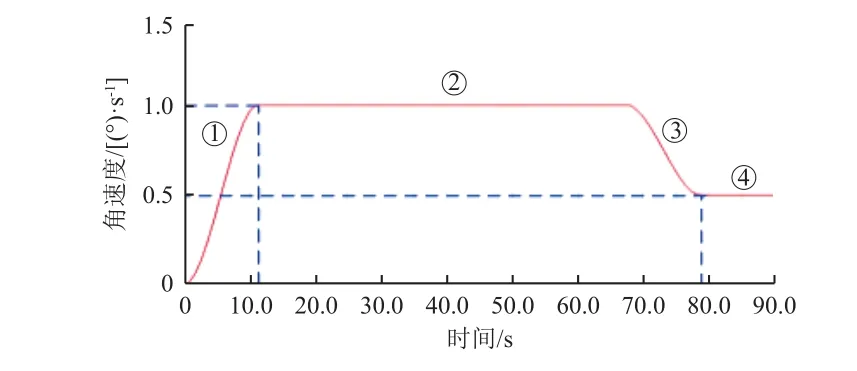
图4 空间薄膜展开机构转动副的驱动函数仿真曲线Fig.4 Drive function simulation curve of the rotating pair of the space membrane deployable mechanism

建立环形桁架式空间薄膜展开机构参数化仿真试验模型。在可靠性仿真试验之前，进行展开机构的运动功能仿真验证，得到展开杆的展开角度变化曲线，如图5(a)所示；选取图3 所示的2#，3#，4#，5#支撑点对应的竖直支撑杆，得到各竖直支撑杆展开位移与角度、展开速度和展开加速度随时间的变化曲线，分别如图5(b)、(c)和(d)所示。由图可知：环形桁架式空间薄膜展开机构的各折展单元的位移、速度和加速度变化趋势基本一致；且展开到位后，每个支撑单元杆展开角度相同。这表明各折展单元均能顺利展开至规定的位置。

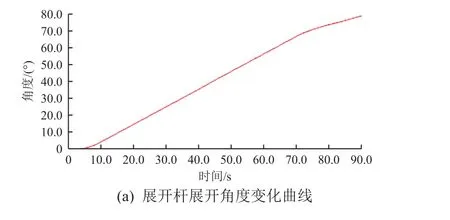
图5 空间薄膜展开机构运动功能仿真结果Fig.5 Motion function simulation results of the space membrane deployable mechanism

3.2 运动精度可靠性仿真求解

调用ADAMS/Insight 模块，完成环形桁架式空间薄膜展开机构在杆长误差影响下的仿真设置。这里，将杆长误差设置为服从正态分布，利用Monte Carlo 法生成随机数。

对环形桁架式空间薄膜展开机构的仿真模型参数化后，添加8 个单元中各自竖直支撑杆端点Di的位置坐标(xDi,yDi,zDi)作为输出量，基于杆长的随机尺寸进行运动精度可靠性仿真，仿真次数为104次[17]。将输出结果导出并进行数据处理，1#折展单元仿真第1～10 次的结果见表3。

表3 基于ADAMS/Insight 的空间薄膜展开机构运动精度可靠性仿真结果Table 3 Motion accuracy reliability simulation results of space membrane deployable mechanism by ADAMS/Insight

通过上述环形桁架式空间薄膜展开机构的运动精度可靠性仿真，输出2#～8#单元竖直支撑杆上端点D的坐标数据与理论标准值求解位置误差，对其分别求解误差参数的均值与均方差值。图6 为可靠性仿真中单次仿真结果的对比。

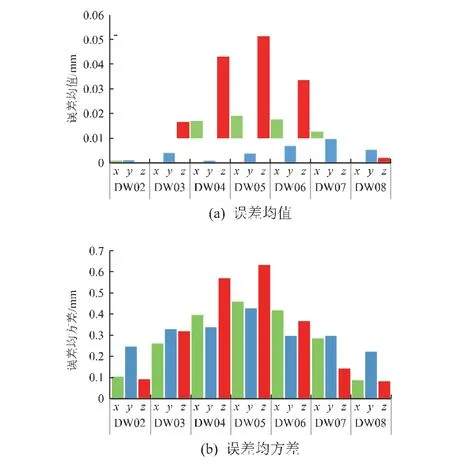
图6 折展单元竖直支撑杆D 点坐标x、y、z 方向误差对比Fig.6 Error comparison of point D coordinate in x, y and z directions for the vertical supporting rod of folding unit

基于MATLAB 将环形桁架式空间薄膜展开机构的8 个支撑点标准坐标进行空间圆拟合，104次的拟合结果如图7 所示。

图7 环形桁架式空间薄膜展开机构支撑点拟合空间圆过程Fig.7 Fitting for the supporting points of annular truss membrane deployable mechanism to a spacial circle

根据最小二乘法拟合的空间圆误差为

式中：S为残差平方和；σS为拟合误差。

确定允许拟合误差为项目允许误差（±1 mm）的1/10[18]，故排除拟合误差超过0.1mm 的拟合结果，得到有效拟合结果为6369 次。

对展开机构展开到位后的拟合空间圆圆心坐标误差与半径误差是否服从正态分布进行拟合，利用Normplot 函数进行正态性检验，结果如图8 所示，其中：红色点划线为正态分布线；蓝色散点为数据点。由图8 可知，空间圆圆心坐标与半径误差不服从正态分布，不能直接计算可靠度[19]。

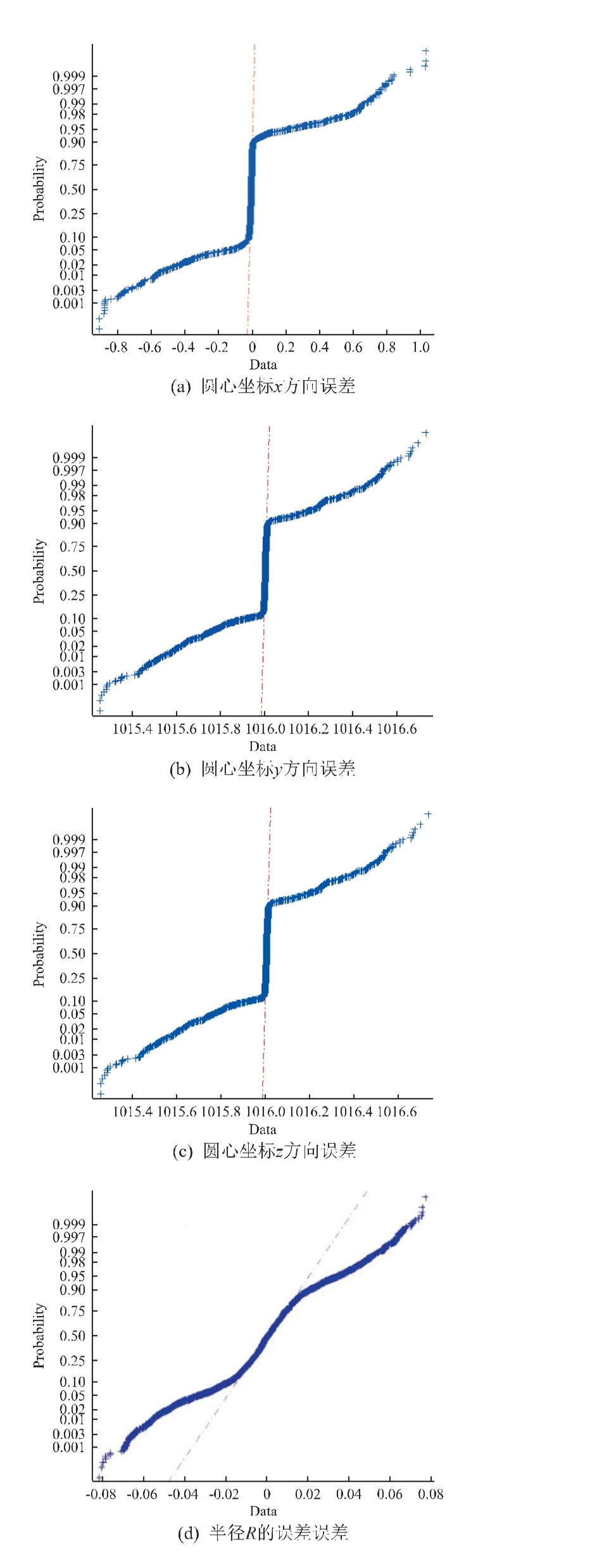
图8 空间圆圆心坐标与半径误差正态分布检验结果Fig.8 Normal distribution test results of spacial circle center coordinate and radius error

故由式(18)计算环形桁架式空间薄膜展开机构的运动精度可靠度，结果为R=RxcRycRzcRr=0.999 5×1×1×1=0.999 5。

4 结束语

本文针对环形桁架式空间薄膜展开机构，完成了机构运动精度可靠性理论建模；基于ADAMS/Insight模块建立了考虑杆长误差的参数化仿真模型，采用蒙特卡罗法进行了模拟试验；利用MATLAB 对输出数据进行了空间圆拟合，得到了相应的圆心坐标及半径，进行了正态分布检验，求解了环形桁架式空间薄膜展开机构的运动精度可靠度。结果显示：在允许误差为±1 mm 时，环形桁架式空间薄膜展开机构的运动精度可靠度为0.999 5。上述研究结果为空间薄膜展开机构的进一步优化设计提供了依据。