自适应正则化滤波化极方法研究
2024-03-11何涛王皓张义蜜王万银ColinFarquharsonKimWelford
何涛, 王皓, 张义蜜, 王万银,2,3*, Colin G. Farquharson,J. Kim Welford
1 长安大学地质工程与测绘学院, 西安 710054
2 海洋油气勘探国家工程研究中心, 北京 100028
3 中国科学院海洋地质与环境重点实验室, 山东青岛 266071
4 Department of Earth Sciences, Memorial University of Newfoundland, St. John′s, AlB 3X5, Canada
0 引言
磁力异常受到斜磁化的影响,对正确认识磁性体造成了困难.所以使用化极处理消除斜磁化的影响,成为利用磁力异常进行解释的首要环节.相比于空间域的褶积方法(Baranov,1957),在波数域(频率域)进行化极仅是简单的乘积运算(Bhattacharyya,1965),其表达式简单且效率更高,但在低纬度地区会出现不稳定性问题.因此众多学者针对低纬度地区化极的不稳定性问题做了大量的研究,提出了许多方法.在空间域,主要为等效源方法(Silva,1986;郭志宏,1997;骆遥和薛典军,2009;Li et al.,2014),该方法计算精度高,但是计算效率低.在波数域(频率域),主要采用滤波方法(Macleod et al.,1993;姚长利等,2003;Li,2008;石磊等,2012;Guo et al.,2013;Zhang et al.,2014;Stewart,2019;Ribeiro,2020)来提高化极的稳定性,其中比较典型的一类就是基于正则化思想的正则化滤波方法,包括维纳滤波法(Hansen and Pawlowski,1989;Keating and Zerbo,1996)、双曲正(余)弦法(张培琴和赵群友,1996)、直接阻尼法(姚长利等,2004;荆磊等,2017)、变频双向阻尼法(林晓星和王平,2012)和正则化法(曾小牛等,2016;张琪等,2018).正则化滤波方法是在化极因子中引入正则化滤波函数,来压制低纬度地区化极因子的放大作用.该类方法的关键在于正则化滤波函数的构建,前人一般采用正弦(余弦)函数,以保证其连续性、有限性,但是其中设计的控制参数较多,关键参数选择标准缺乏理论研究,从而降低了方法的实用性.因此为提高方法的实用性,当前广泛利用受磁化方向影响较小的磁场转换量与化极结果的相关系数来确定方法的参数(Dannemiller and Li,2006;Gerovska et al.,2009;Zhang et al.,2014;Rao et al.,2016;Li et al., 2017;Zhang et al.,2018;Hao et al.,2018).常见的受磁化方向影响较小的磁场转换量主要是解析信号振幅(Nabighian,1972)、磁场模量及其相关转换量(Stavrev and Gerovska,2000;Gerovska and Araúzo-Bravo,2006)以及归一化磁源强度(Wynn et al.,1975).其中,解析信号振幅较易获得,应用最为广泛,但是三度体的解析信号振幅仍然会受到磁化方向的强烈影响,此外还受地质体的埋深影响(Li,2006;王万银,2012).而磁场模量及其相关转换量和归一化磁源强度需已知磁场三分量才能有效地降低磁化方向的影响,但是在实际工作中,较多的情况为仅已知磁场总场,在低纬度地区,利用磁场总场求取磁场三分量同样存在不稳定性问题.故通过相关性确定化极方法的参数存在局限性,不能从根本上解决参数选择的问题.
此外,正则化滤波方法在压制放大作用的同时,由于其滤波尺度难以把握,所以普遍存在滤波过剩现象,损失了有用信号,降低了该类方法化极结果的精度.而迭代方法(Strakhov and Devitsyn,1965;徐世浙,2006)是解决位场数据处理与转换的不稳定性问题的另一重要方法,在低纬度地区的化极处理中也得到了广泛应用(Li,2008;骆遥和薛典军,2010;姚长利等,2012;Hao et al.,2018;He et al.,2022),该类方法仅需近似的化极因子,然后利用原始磁力异常进行约束,通过多次计算提高化极结果的精度.因此将构建的正则化化极因子作为一个近似因子,代入迭代过程,可以有效地提高正则化滤波方法的精度.上述所有研究者均聚焦于低纬度地区具体化极方法的研究,但是关于其应用条件“低纬度地区”这个概念的界定却十分模糊,即缺少高、低纬度地区的分界问题的研究.
综上,明确低纬度地区的范围和研究实用性强、精度高的低纬度地区化极方法具有重要意义.为此,本文依据理论研究确定了化极因子振幅引起放大作用的临界值,进而确定高、低纬度地区磁化倾角的分界值;其中,在低纬度地区依据正则化思想,提出自适应正则化滤波化极方法(The adaptive regularization filtering method of reduction-to-the-pole,ARF-RTP),并通过理论研究确定不同磁化倾角条件下该方法的参数值,提高方法的实用性.同时,结合迭代法解决正则化滤波作用导致的有用信号损失问题,提高方法的精度,有效地解决低纬度地区化极的不稳定性问题.最后,通过理论模型测试和实际资料处理验证了该方法的正确性、稳定性和实用性.
1 化极因子特征分析
波数域(频率域)磁场分量和磁化方向转换因子H(u,v)为(Bhattacharyya,1965)
H(u,v)=
(1)

将(1)式转换至极坐标,得到极坐标下转换因子表现形式H(θ)(Mendonça and Silva,1993):
(2)
式中,θ=arctan(v/u).如果仅进行磁化方向转换,式中保持分量方向在转换前后不变即可.同理,磁场分量方向转换也是相同.
当磁场分量方向和磁化方向一致时,(2)式可以简化为(Mendonça and Silva,1993)
(3)
磁场分量和磁化方向转换中最常使用的是化极(Reduction-to-the-pole,RTP),即转换到垂直磁化的垂直分量(I2=90°),其转换因子(Mendonça and Silva,1993)为
(4)
将其分解为振幅ARTP(θ)和相位φRTP(θ)形式(荆磊等,2017):
(5)
在波数域(频率域)转换时,振幅相乘,而相位则是执行相加运算.(5)式中相位满足-180°≤φRTP(θ)≤180°,在转换中仅起到改变原始波谱相位的作用,不会引起不稳定性问题,而振幅ARTP(θ)值域与磁化倾角I1相关,其参与的相乘运算会导致不稳定性问题.为了进一步说明化极因子振幅和相位特征,做出其相应的等值线图(图1).

图1 全倾角化极因子的振幅与相位等值线图(a) D=0°振幅; (b) D=0°相位; (c) D=45°振幅; (d) D=45°相位. 振幅图中等值线间隔按照对数函数(ln函数)值分布规律进行设置;振幅图中最大值为无穷大,为了便于成图,设置色标最大值为1000;相位图中等值线间隔为30.
对比图1a和图1c可以看出化极因子振幅在南、北半球变化特征相同,呈现明显的对称性,最小值为1;各磁化倾角的振幅均在θ-D=±90°处达到最大值,随着磁化倾角的减小,最大值逐渐增大,而磁化偏角决定了振幅放大的位置,但它本身不会影响振幅的放大效果.对比图1b和图1d可以看出相位的范围始终在-180°~180°之间,在θ-D=±90°时相位为0,在θ-D=±90°两侧由正(负)相位变为负(正)相位,随着磁化倾角的减小,相位曲线变得陡峭,而磁化偏角决定了相位反相的位置.
图1中,各振幅均以2为界(图中白色实线)呈现不同的特征.当振幅小于2时,等值线呈现非圆形特征,变化较缓慢,随着幅值逐渐增大,形状收敛于以放大中心(θ-D=±90°,0°)为圆心的圆形;当振幅等于2时,等值线形成以(θ-D=±90°,0°)为圆心,半径为45°的圆形;当振幅大于2时,等值线依旧保持以(θ-D=±90°,0°)为圆心的圆形特征,但是其等值线代表的值急剧增大,至圆心趋于无穷(各振幅图中最大值为无穷大,但网格化后显示为特征值,所以振幅图的色标显示有界,在这里为了便于成图,最大值设置为1000),说明在幅值2形成的圆内,无论是纵轴I还是横轴θ,其趋近于圆心(θ-D=±90°,0°)方向的相同变化量所引起振幅的变化量也是相同的,这种变化接近圆心时趋于无穷.
为了更清晰的研究化极因子振幅变化的特征,在这里使用总水平导数(Cordell,1979)研究其变化率,化极因子振幅总水平导数如图2所示.
图2显示振幅总水平导数以振幅2为界(图中白色线条).当振幅小于2时,振幅无论是在横轴I方向还是纵轴θ方向变化率均较小,其总水平导数值小于0.1;而当振幅大于2时,振幅变化剧烈,总水平导数值大于0.1且急剧增大,反映了振幅正向增大的变化趋势,在(θ-D=±90°,0°)处振幅变化率同振幅一样趋于无穷.
化极因子振幅无界,而最小值仅为1,幅值的量级变化非常大,讨论中受大值的影响,弱小信号会被湮没.而且在总水平导数计算过程中,其计算结果受网格间距影响较大,为使结果更具普适性,我们希望得到总水平导数特征的分界性而非幅值的分界,所以结合化极的反变换过程进行讨论,即由化极场转换到任意低纬度磁场的过程,该转换因子的振幅ARTP→Lowfield(θ)为
ARTP→Lowfield(θ)=cos2(I1)·cos2(θ-D1)+sin2(I1),
(6)
该因子与ARTP(θ)互为倒数,幅值在0~1之间,同样对其进行求导分析.

图2 全倾角化极因子振幅的总水平导数等值线图(a) D=0°振幅总水平导数; (b) D=45°振幅总水平导数. 等值线间隔按照对数函数(ln函数)值分布规律进行设置;图中白色线条表示振幅值为2的等值线.
图3表示ARTP→Lowfield(θ)的振幅以及其总水平导数图.该振幅(图3a,图3c)和化极因子振幅特征相同,在南、北半球呈现明显的对称性,最小值在(θ-D=±90°,0°)处,幅值为0.分别求其总水平导数得到图3b,图3d,其最大值反映了ARTP→Lowfield(θ)最大变化率,恰在ARTP→Lowfield(θ)=0.5(图中白色实线)处,当ARTP→Lowfield(θ)>0.5时,随着ARTP→Lowfield(θ)值减小,总水平导数值增大,说明其变化率增大,对应的ARTP(θ)<2;当ARTP→Lowfield(θ)=0.5时,其对应的ARTP(θ)=2;当ARTP→Lowfield(θ)<0.5时,随着ARTP→Lowfield(θ)值减小,总水平导数值也减小,说明其变化率减小,其对应的ARTP(θ)>2.所以0.5是ARTP→Lowfield(θ)幅值变化特征的分界,与之对应的2是ARTP(θ)幅值变化特征的分界.
结合ARTP(θ)的特征、ARTP(θ)的变化率特征、ARTP→Lowfield(θ)的特征以及ARTP→Lowfield(θ)的变化率特征,可以看出当ARTP(θ)≤2时,虽然其值逐渐变大但是其变化率较小,振幅最大值与最小值的偏差在0~1之间,保持稳定状态;当ARTP(θ)>2时,ARTP(θ)其值依旧保持变大趋势,但是其变化率较大,振幅在θ-D=±90°左右两侧对称的扇形范围内开始大于2,而且随着|I|的减小,这个扇形范围增大,扇形范围内振幅的值也增大,振幅最大值与最小值的偏差大于1,并趋于无穷,为不稳定状态.综上,幅值2为化极因子振幅稳定与非稳定状态的分界,其对应的磁化倾角|I|=45°,而|I|<45°的范围则为化极过程中存在不稳定问题的低纬度地区.

图3 全倾角化极场转换低纬度地区磁场转换因子的振幅与总水平导数等值线图(a) D=0°振幅; (b) D=0°振幅总水平导数; (c) D=45°振幅; (d) D=45°振幅总水平导数. 总水平导数图中白色线条表示振幅值为0.5的等值线;振幅图中等值线间隔为0.1;水平导数图中等值线间隔为0.001.
2 自适应正则化滤波化极方法
位场数据的处理和转换通常存在这样一类问题,其转换因子是如下的分数形式:
(7)
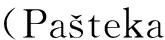
(8)
其中,对正则化滤波函数R(θ)的基本要求是该函数的引入仅是提高转换因子的稳定性,但是不能改变转换因子的基本特征.那么简单、高效的正则化滤波函数的求取是提高正则化方法实用性的关键.
2.1 自适应正则化滤波方法
化极因子的振幅形式类同于公式(7),其放大作用是由振幅的分母趋于零所引起的,因此可以利用正则化思想,通过在振幅的分母上引入正则化滤波函数,去压制放大作用.
在这里我们利用化极因子振幅构建正则化滤波函数:
(9)
式中,α为正则化因子,是一个非负实数,用来调节正则化滤波函数作用的大小.将(9)式引入到化极因子振幅的分母并化简,得到正则化的化极因子振幅:
Regulation_ARTP(θ)=
(10)
此时构建的正则化的化极因子振幅的分子与分母变化规律保持一致,可以实现自适应抑制化极因子振幅的放大作用,而且无须设置多余参数,在使用中仅需确定正则化因子α的值即可.
前文分析了化极因子的特征,其放大作用是由于振幅大于2所引起的,而振幅在1~2之间是稳定的,所以为了尽可能地保留化极因子本身的有效信号,同时提高稳定性,我们采用区域正则化,此时构建的正则化振幅AARF-RTP(θ)为如下形式:
(11)
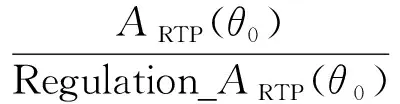
以上就是自适应正则化滤波化极方法的基本原理,其化极因子为如下形式:
ARF_HRTP(θ)=AARF-RTP(θ)·eiφRTP(θ),
(12)
其中,AARF-RTP(θ)表达见式(11),φRTP(θ)表达见式(5).因此,利用自适应正则化滤波化极方法计算化极场的具体公式如下:
RTP(θ)=[AARF-RTP(θ)·AΔT(θ)]·ei[φRTP(θ)+φΔT(θ)],
(13)
其中,RTP(θ)表示化极场波谱;AΔT(θ)为原始磁场振幅,与上文构建的自适应正则化振幅相乘;φΔT(θ)为原始磁场相位,与化极因子本身的相位相加.
2.2 正则化因子α的确定
本文通过理论研究确定正则化因子α的值.当α取不同值,可以得到不同θ处的AARF-RTP(θ)值,选择其最大值构建如下函数:
f(α)=max[AARF-RTP(θ)].
(14)
前文分析可知,当振幅大于2时,存在放大作用,因此以2作为约束,使f(α)函数满足下列条件:
f(α)≤2.
(15)
满足上述条件的α存在无穷多个,但是α越大,滤波作用越强,可能会出现过滤波问题,因此选择该条件下的最小α值,既保证了稳定转换,同时减小过滤波的影响.根据上述分析计算得到不同磁化倾角对应的最佳的α值(见表1).

表 1 各磁化倾角对应的α值表Table 1 α corresponding to each magnetization inclination
表1给出了各整数磁化倾角对应的α值,当磁化倾角为小数时,选择其相邻的两个整数磁化倾角对应的α值中的最大值即可,以保证完全压制.
将各倾角确定的α值代入式(11),得到全倾角自适应正则化滤波化极因子的振幅特征图(图4,可以看出该正则化振幅保持了其原来振幅对称性和连续型的特征,而且当|I|<45°时,正则化振幅最大值为2(图4a),在θ-D=±90°处达到极小值,向两侧对称的增大,直至达到最大值2之后又开始减小(图4b),但是部分倾角的最小值小于1,说明该正则化振幅可实现稳定转换,但是会引起信号损失.

图4 全倾角自适应正则化滤波化极因子振幅图(a) 振幅(D=0°); (b) 不同磁化倾角振幅对比(D=0°). 等值线间隔为0.1.
2.3 迭代法提高化极精度
滤波类化极方法的化极结果适用于定性解释,不利于定量解释(柴玉璞和万海珍,2020),其主要原因是在提高化极稳定性的同时,导致化极损失效应增强,进而影响化极结果的精度.而本次研究的自适应正则化滤波化极方法也属于滤波类方法,虽然其尽可能地保留了化极因子本身的有效信号,但依旧会产生损失效应.所以结合迭代法,以原始磁力异常作为约束,通过多次计算削弱损失效应,提高化极结果精度.
位场中数据转换的迭代法收敛通式为(姚长利等,2012)
|1-φ(θ)κ-1(θ)|<1,
(16)
其中,φ(θ)为近似转换因子,在这里为式(11)表示的正则化振幅因子;κ(θ)为真实转换因子,即式(5)中的真实振幅因子,将其代入(16)式得到:
(17)
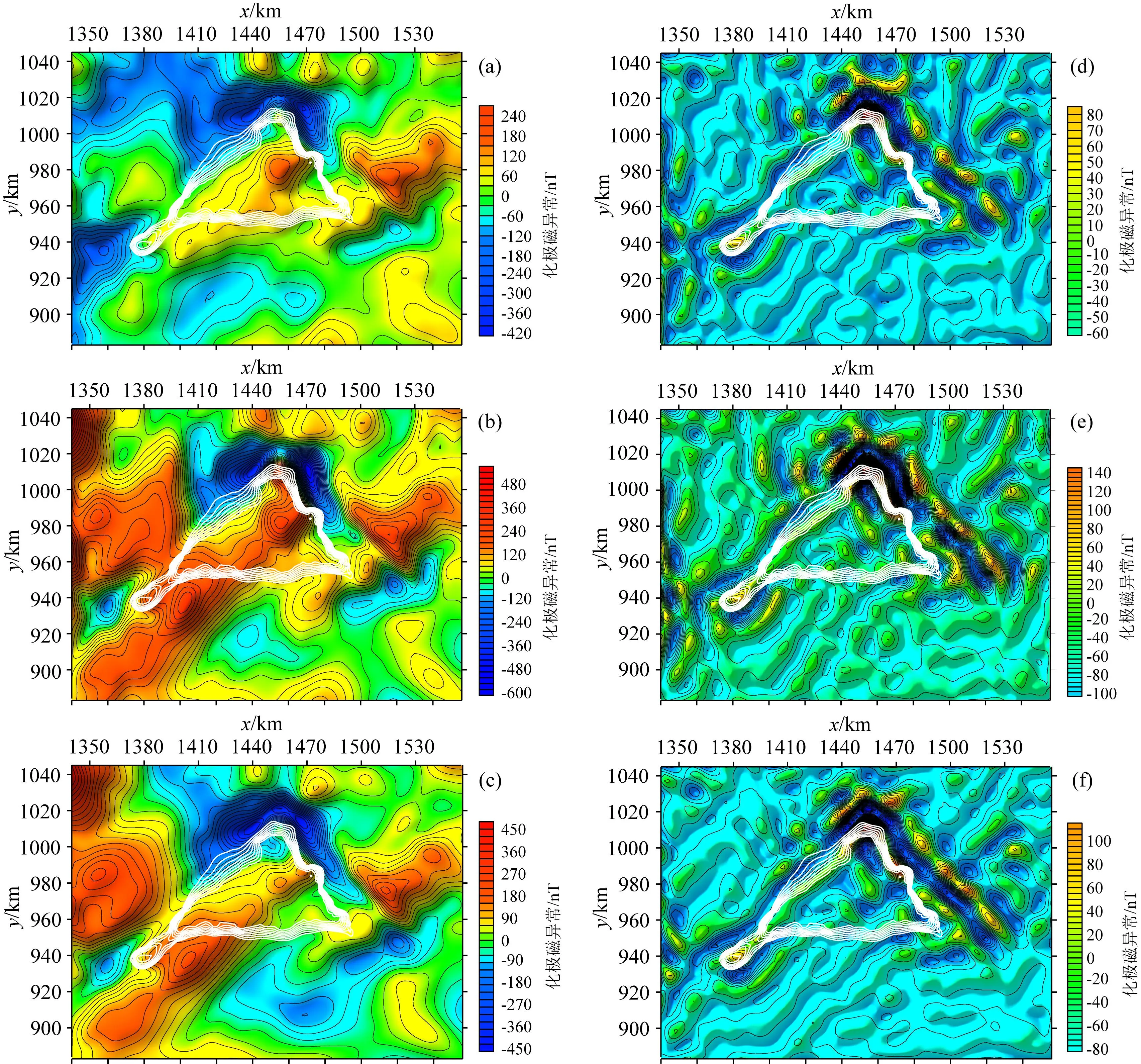
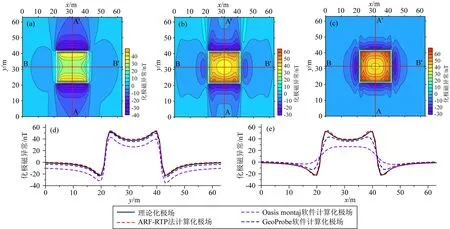
式中0 具体迭代流程(图5)如下: 图5 迭代法化极流程图 (1)根据式(13),进行自适应正则化滤波化极,得到初始化极磁力异常(RTP(1)). (2)利用化极磁力异常(RTP(1))计算磁力异常(ΔT(1)). (3)利用原始磁力异常ΔT与计算磁力异常ΔT(1)求取残差,即δΔT(1)=ΔT-ΔT(1). (4)判断残差δΔT(1)是否满足精度控制条件:δΔT(1)<ε(ε为迭代控制误差).满足精度条件,输出化极场;不满足精度条件,返回到步骤(1)对残差δΔT(1)进行正则化滤波化极处理,然后利用残差化极场δRTP(1)对初始化极磁力异常RTP(1)进行校正,得到RTP(2)=RTP(1)+δRTP(1). 依次重复以上步骤直到残差δΔT(k)满足控制要求输出化极异常RTP(k)即可. 化极转换是磁化方向和磁场分量同时进行转换的问题,因此当我们仅执行分量转换或者磁化方向单一转换时,均可按照上述的原理进行处理. 本研究分别设计单一模型和复杂模型模拟实际地质体测试方法的正确性和稳定性.采用目前较为广泛应用的商业软件Geosoft的Oasis montaj软件(8.4版本)和GeoProbe软件(4.0版本)与本文ARF-RTP方法进行化极效果对比.Oasis montaj软件中化极方法为伪倾角法;GeoProbe软件中化极方法选择为双曲余弦滤波法,上述两个软件所使用的相关参数为多次测试后化极效果较为理想的参数.通过求取理论化极磁力异常与计算得到的化极磁力异常之间的均方根误差: (18) 相对均方根误差: (19) 说明各个方法的精度.其中,M,N为点数和线数,RTP(i,j)表示第(i,j)点上正演的理论化极磁力异常值,RTPcal(i,j)表示第(i,j)点上计算得到的化极磁力异常值,RTPmax表示理论化极磁力异常的最大值,RTPmin表示理论化极磁力异常的最小值. 下文各图中白色线框表示形体的平面位置,文中计算得到的化极磁力异常与其对应的理论化极磁力异常的色标以及等值线间隔均保持一致. 单体模型选择由Hansen和Pawlowski(1989)设计的模型,该模型被众多学者用来测试各方法的化极效果,模型具体参数见表2(x1、x2,y1、y2,z1、z2分别为各直立六面体沿x,y,z方向的范围),设置观测界面为z=0.0 m(z坐标方向铅垂向下为正). 图6a为单体模型正演的I=0°磁化磁力异常;图6b为正演的I=90°磁化磁力异常,异常值在-22.43~62.40 nT之间,异常幅值为84.83 nT.为了更加直观的对比各个方法的化极效果,设置了通过主异常体的A-A′剖面(x=31.5 m)与B-B′剖面(y=31.5 m)(图6b中红色线条)对比化极结果. 表2 单体模型参数及测网参数表Table 2 Parameters and measurement network of the simple model 图6 单体模型正演磁力异常图(a) I=0°磁化磁力异常; (b) I=90°磁化磁力异常. 图中等值线间隔均为5 nT. 图7 单体模型磁力异常化极结果图(a) Oasis montaj软件化极结果; (b) GeoProbe软件化极结果; (c) ARF-RTP法化极结果; (d) A-A′剖面化极结果对比图; (e) B-B′剖面化极结果对比图. 图中白色线框表示形体平面位置,等值线间隔均为5 nT. 图7为图6a表示的磁力异常的化极结果.Oasis montaj软件中Amplitude correction inclination选择为20°,GeoProbe软件中滤波参数AS选择为12,BS选择为0.0001,本文ARF-RTP法中α值选择0.242. Oasis montaj软件(图7a)和GeoProbe软件(图7b)的化极结果在异常体正上方与理论化极异常(图6b)特征相差较大,受沿磁化偏角方向的拉伸现象的影响,并未完全形成与理论化极异常一致的圆弧形圈闭异常特征.本文ARF-RTP法计算的化极结果(图7c)明显减弱了沿磁化偏角方向的拉伸现象的影响,基本恢复了异常体正上方的异常特征.通过A-A′剖面(图7d)和B-B′剖面(图7e)整体可以看出,本文ARF-RTP法化极结果更接近理论化极异常,其次为GeoProbe软件,Oasis montaj软件效果最差.Oasis montaj软件、GeoProbe软件以及ARF-RTP法化极结果的均方误差和相对均方误差统计见表3,ARF-RTP法精度明显优于上述两个软件.细节方面,在A-A′剖面(图7d)方向ARF-RTP法、GeoProbe软件、Oasis montaj软件化极结果形态与理论异常形态基本一致,但是Oasis montaj软件化极结果与理论化极磁力异常存在背景差,而ARF-RTP法与GeoProbe软件化极结果没有表现出明显的背景差;在B-B′剖面(图7e)方向ARF-RTP法化极结果与理论异常形态基本一致,GeoProbe软件、Oasis montaj软件化极结果较理论异常光滑,表明GeoProbe软件和Oasis montaj软件方法在压制放大作用的同时,对垂直于磁化偏角方向的有效信息进行了较强的滤波. 表3 单体模型磁力异常化极结果误差统计表Table 3 Error statistics of RTP results of magnetic anomaly of the simple model 复杂模型选择由He等(2022)使用的模型,该模型利用五个大小、埋深各不相同的直立六面体构成.模型具体参数见表4,各参数代表意义与上述单体模型相同,设置观测界面为z=0.0 km. 表4 复杂模型参数及测网参数表Table 4 Parameters and measurement network of the complex model 图8 复杂模型正演磁力异常图(a) I=0°磁化磁力异常; (b) I=10°磁化磁力异常; (c) I=30°磁化磁力异常; (d) I=10°磁化含噪声磁力异常; (e) I=90°磁化磁力异常. 图中白色线框表示形体平面位置,等值线间隔为50 nT. 图9 复杂模型磁力异常化极结果(a) I=0°磁力异常Oasis montaj软件化极结果; (b) I=0°磁力异常GeoProbe软件化极结果; (c) I=0°磁力异常ARF-RTP法化极结果; (d) I=10°磁力异常Oasis montaj软件化极结果; (e) I=10°磁力异常GeoProbe软件化极结果; (f) I=10°磁力异常ARF-RTP法化极结果; (g) I=30°磁力异常Oasis montaj软件化极结果; (h) I=30°磁力异常GeoProbe软件化极结果; (i) I=30°磁力异常ARF-RTP法化极结果. 图中白色线框表示形体平面位置,等值线间隔均为50 nT. 图10 复杂模型磁力异常不同方法化极结果对比(a) A-A′剖面I=0°磁力异常化极结果对比图; (b) B-B′剖面I=0°磁力异常化极结果对比图; (c) A-A′剖面I=10°磁力异常化极结果对比图; (d) B-B′剖面I=10°磁力异常化极结果对比图; (e) A-A′剖面I=30°磁力异常化极结果对比图; (f) B-B′剖面I=30°磁力异常化极结果对比图. 图11 复杂模型含噪声磁力异常化极结果图(a) Oasis montaj软件化极结果; (b) GeoProbe软件化极结果; (c) ARF-RTP法化极结果; (d) A-A′剖面化极结果对比图; (e) B-B′剖面化极结果对比图. 文中所加噪声选择均值为0 nT,标准偏差为3 nT的高斯噪声,图中白色线框表示形体平面位置,等值线间隔均为50 nT. 图8(a,b,c)分别表示复杂模型正演的I=0°,I=10°,I=30°磁化磁力异常图;图8d表示对图8b表示的磁力异常加均值为0 nT,标准偏差为3 nT高斯噪声的含噪声磁力异常;图8e为正演的I=90°磁化磁力异常,异常值在-144.11-1092.29 nT之间,异常幅值为1236.40 nT.选择A-A′剖面(x=7 km)与B-B′剖面(y=12 km)(图8e中红色线条)进行化极结果剖面对比. 图9为图8a、图8b、图8c表示的磁力异常的化极结果.其中,在I=0°时,Oasis montaj软件中Amplitude correction inclination选择为10°,GeoProbe软件中滤波参数AS选择为6,BS选择为0.001,本文ARF-RTP方法中α值选择0.242;在I=10°时,Oasis montaj软件中Amplitude correction inclination选择为15°,GeoProbe软件中滤波参数AS选择为12,BS选择为0.001,本文ARF-RTP方法中α值选择0.250;在I=30°时,Oasis montaj软件中Amplitude correction inclination选择为30°,GeoProbe软件中滤波参数AS选择为12,BS选择为0.0001,本文ARF-RTP方法中α值选择0.249. 当I=0°与I=10°时,Oasis montaj软件(图9a,图9d)和GeoProbe软件(图9b,图9e)的化极结果中主体异常特征基本恢复,但是在形体的南北两侧均存在沿磁化偏角方向的拉伸现象,形成条带状虚假异常.而ARF-RTP法计算的化极结果(图9c)中沿磁化偏角方向的拉伸现象明显减弱,在I=10°时,其化极结果(图9f)已不存在拉伸现象,异常形态更接近理论异常形态.当I=30°时,Oasis montaj软件(图9g)与GeoProbe软件(图9h)化极结果中已无明显的沿磁偏角方向的拉伸现象,与理论异常形态较为接近,ARF-RTP法化极结果(图9i)与理论异常在形态和幅值上基本保持一致.不同磁化倾角条件下,Oasis montaj软件、GeoProbe软件以及ARF-RTP法的均方误差和相对均方误差统计见表5,ARF-RTP法精度明显优于上述两个软件,而且磁化倾角越小,这种优势越明显. 细节方面,与单体模型相同,在A-A′剖面(图10a,图10c)方向ARF-RTP法、GeoProbe软件、Oasis montaj软件化极结果形态与理论异常形态基本一致,但是在异常体上方(10 km至22 km之间)Oasis montaj软件与GeoProbe软件化极结果的幅值整体偏小,似乎存在背景差的影响,而ARF-RTP法化极结果与理论异常曲线基本重合;在B-B′剖面(图10b,图10d)方向ARF-RTP法化极结果与理论异常形态基本一致,GeoProbe软件、Oasis montaj软件化极结果较理论异常光滑,尤其在异常局部凸起和凹陷处(3~10 km之间)这种光滑现象尤为明显,反映了GeoProbe软件和Oasis montaj软件方法在压制垂直于磁化偏角方向的放大作用的同时,会对有效信息进行滤波.当I=30°时,在A-A′剖面(图10e)与B-B′剖面(图10f)处,ARF-RTP法、GeoProbe软件、Oasis montaj软件化极结果曲线与理论异常曲线基本重合. 图11为图8d所示的含噪声磁力异常的化极结果.Oasis montaj软件中Amplitude correction inclination选择为15°,GeoProbe软件中滤波参数AS选择为12,BS选择为0.001,本文ARF-RTP方法中α值选择0.250.添加噪声后,Oasis montaj软件(图11a)、GeoProbe软件(11b)和ARF-RTP法(图11c)计算的化极结果的异常形态与不含噪声磁力异常化极结果基本是一致的,仅是受噪声影响异常曲线存在锯齿状波动.剖面图11d和图11e显示存在噪声时,ARF-RTP法的化极结果仍然更接近理论化极场,而且异常曲线波动较小.各方法均方误差与相对均方误差统计见表5,当磁力异常含噪声时,ARF-RTP法对噪声可以进行较好的压制,化极结果的精度依旧明显优于Oasis montaj软件和GeoProbe软件. 表5 复杂模型磁力异常化极结果误差统计表Table 5 Error statistics of RTP results of magnetic anomaly of the complex model 为了测试方法在不同低纬度地区的实际资料处理中的实用性,选择位于磁赤道附近的Magur Islands研究区ΔT磁力异常(磁化倾角为2.78°,磁化偏角为3.66°)和纬度相对较高的惠北凹陷研究区ΔT磁力异常(磁化倾角29.0°,磁化偏角为-1.43°)分别进行化极处理. Magur Islands研究区位于卡罗琳板块与太平洋板块交界处,图12为其ΔT磁力异常图,该数据来源于EMAG2(V2)地磁网格(Earth Magnetic Anomaly Grid,2-arc-minute resolution).Magur Islands是卡罗琳板块热点的产物,属于火山岩岛屿,具有高磁特性(Wu et al., 2016),但是ΔT磁力异常呈现明显的低磁异常特征,而高磁异常主要分布在火山南北两侧,这是典型的磁赤道附近磁性体磁力异常的表现,这种异常特征与已知地质认识不符,需对其进行化极处理. 图12 Magur Islands研究区ΔT磁力异常图图中白色线条表示Magur Islands平面位置,等值线间隔为20 nT. 对图12所表示ΔT磁力异常进行化极处理得到化极磁力异常(图13).其中,Oasis montaj软件中Amplitude correction Inclination选择为60°,GeoProbe软件中滤波参数AS选择为2,BS选择为0.1,本文ARF-RTP方法中α值选择0.242.Oasis montaj软件(图13a)、GeoProbe软件(图13b)和ARF-RTP法(图13c)三类方法化极结果的异常特征大致相似,在Magur Islands处均对应高磁异常,整体呈现NE向高低值相间分布的条带特征,是太平洋洋壳磁条带的典型表现,与已知地质认识相符合.为了更加清楚的表现其化极结果是否稳定,即是否存在近NS向虚假异常,对上述化极结果进行分离,得到分离后的剩余化极磁力异常.Oasis montaj软件(图13d)与GeoProbe软件(图13e)的剩余化极磁力异常在研究区西部以及北部存在明显的近NS向的条带状异常,这种近NS向异常并非构造特征的表现,其主要是由低纬度地区化极的不稳定所引起的,由于近NS向的条带状虚假异常的影响,使分离的剩余化极场表现为NNE向与NNW向,而非研究区地质构造的NE与NW向.而ARF-RTP法的剩余化极磁力异常(图13f)并未出现近NS向的条带状异常,走向为NE向与NW向,与已知地质构造认识相符.剩余化极磁力异常的特征说明Oasis montaj软件与GeoProbe软件稳定性较差,而本文ARF-RTP方法稳定性更高. 惠北凹陷研究区位于我国著名的含油气盆地珠江口盆地内部,其ΔT磁力异常如图14所示(图中白色实线表示研究区内构造单元界线),该数据来源于南海北部海域的航测ΔT磁力异常平面图. 对图14所表示ΔT磁力异常进行化极处理得到化极磁力异常(图15).其中,Oasis montaj软件中Amplitude correction Inclination选择为35°,GeoProbe软件中滤波参数AS选择为12,BS选择为0.005,本文ARF-RTP方法中α值选择0.25.化极之后,异常正值向北偏移,GeoProbe软件(图15b)和ARF-RTP法(图15c)化极结果的异常特征大致相似,但是Oasis montaj软件化极结果(图15a)与二者相差较大,在惠州凹陷南部仍然是低磁异常,而GeoProbe软件和ARF-RTP方法在该处已过渡至高磁异常,可能是Oasis montaj软件中在压制放大作用的过程中使用了大于实际磁化倾角的Amplitude correction Inclination导致异常正值向北偏移不足.同样为了检验其化极结果是否稳定,对化极磁力异常分别进行分离,得到分离后的剩余化极磁力异常.Oasis montaj软件(图15d)、GeoProbe软件(图15e)与ARF-RTP法(图15f)化极结果分离得到的剩余化极磁力异常特征相近,均未表现出近NS向的条带状特征,说明三类方法的化极结果均是稳定的. 本文通过理论研究得到,在化极处理过程中化极因子振幅稳定与否的临界值为2,与之对应的磁化倾角为±45°;当振幅大于2时,磁化倾角在-45°~45°之间,该范围为低纬度区域,化极处理存在不稳定性问题.为实现低纬度地区稳定地自适应化极处理,本文依据正则化思想,利用化极因子振幅构建正则化滤波函数,进而提出了低纬度地区自适应正则化滤波化极方法(ARF-RTP),在该方法中以临界值2为约束,经过理论推导得到各磁化倾角对应的正则化因子的值,提高了方法的实用性;同时结合迭代通过多次计算提高了方法的精度,有效地解决了低纬度地区化极的不稳定性问题.通过理论模型试验和实际资料处理验证了本文提出的低纬度自适应正则化滤波化极方法的正确性、稳定性和实用性,而且其处理效果明显优于目前主流重、磁处理软件(GeoProbe和Oasis montaj). 本次研究是以固定磁化方向条件为前提,后续还需研究该方法在变磁化方向条件下的应用. 图13 Magur Islands研究区化极磁力异常图(a) Oasis montaj软件化极结果; (b) GeoProbe软件化极结结果; (c) ARF-RTP方法化极结果; (d) 图13a的剩余化极磁力异常; (e) 图13b的剩余化极磁力异常; (f) 图13c的剩余化极磁力异常. 图中白色线条表示Magur Islands平面位置,化极磁力异常等值线间隔均为30 nT,剩余化极磁力异常等值线间隔为5 nT. 图14 惠州凹陷研究区ΔT磁力异常图图中白色线条表示构造单元界线,等值线间隔为10 nT. 致谢感谢论文评审专家提出的修改意见,也感谢本文编辑对论文的加工和修改.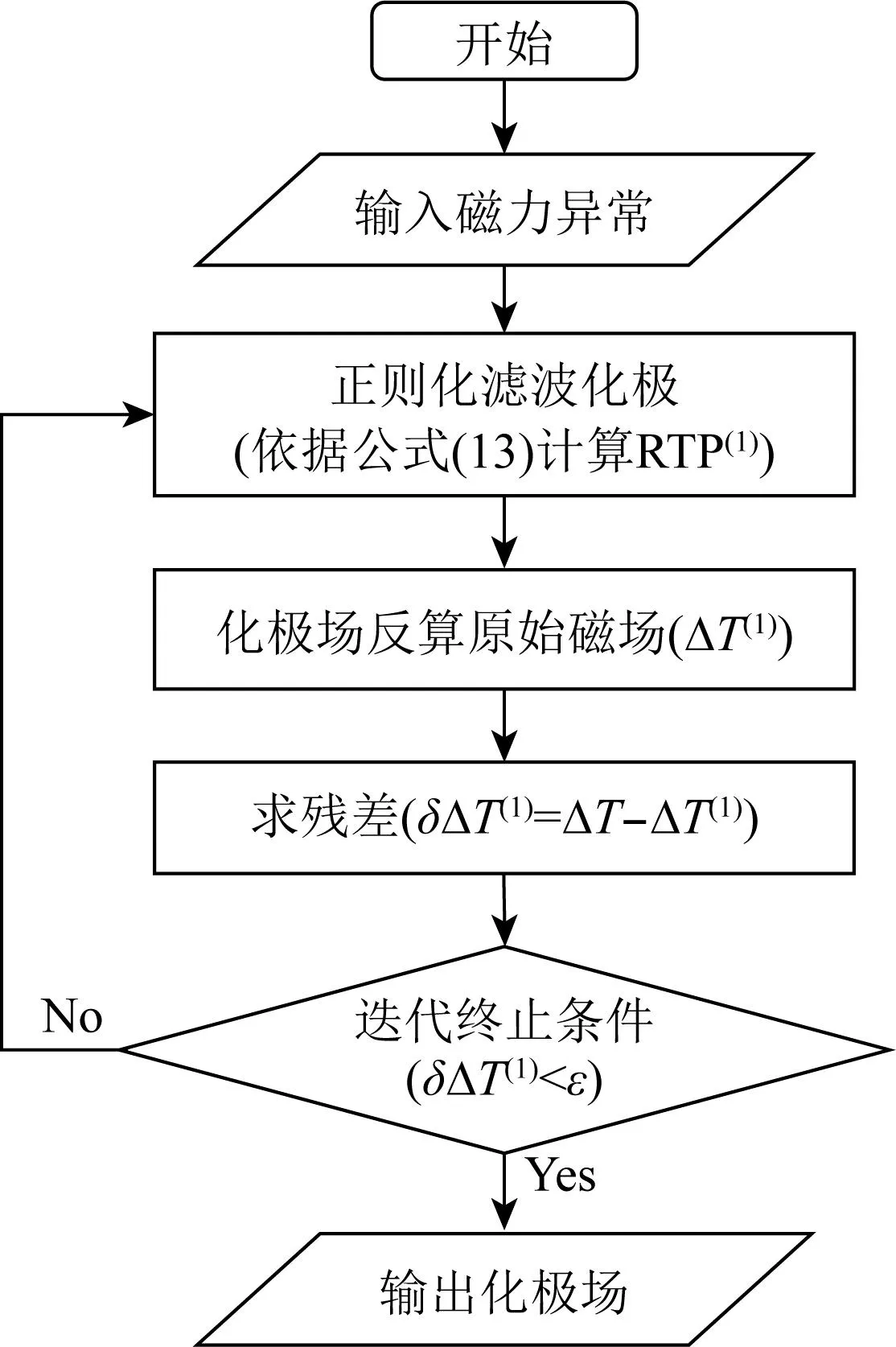
3 模型试算
3.1 单体模型测试



3.2 复杂模型测试






4 实际资料处理

5 结论及建议