长宁—昭通页岩气示范区小微地震地方性震级测定

陈颖, 田雯*, 吴庆举*, 姚志祥

1 中国地震局地球物理研究所, 北京 100081

2 中国地震局地震观测与地球物理成像重点实验室, 北京 100081

0 引言

震级是对地震强度大小的度量.在场地条件相似的前提下,地震的震级越高,其引发的灾害也就越严重,因此震级成为地震应急响应、地震救援和灾害损失评估的一个关键指标.根据地震震级及与震级有关的震源参数统计关系,还可以定量估算其他震源参数,例如地震的能量、地震矩、震源破裂时间、断层长度以及断层面积等(刘瑞丰等,2015).基于地震震级和地震频度之间关系反演获得的b值,常被作为一个反映区域构造应力状况的参考指标(Bender,1983;Schorlemmer et al.,2005).不论是从地震学基础理论研究的视角,还是从防震减灾的实际需求出发,精确测量震级的大小均是一项具有深远意义的重要工作(刘瑞丰等,2015).

1935年,里克特在美国南加州首次引入了震级的概念(Richter,1935),称为地方性震级ML.1959年,李善邦根据我国常用的两种地震仪(62型、64型短周期地震仪和SK型中长周期地震仪)的特性,分别建立了量规函数R1和R2,提出了我国地方性震级标度ML(李善邦,1981).由于我国地域辽阔、地质结构复杂,难以采用统一的量规函数准确测量所有的地震震级,大量的研究结果也证明了这一观点(王丽艳等,2016).1999年,许绍燮等编制了《地震震级的规定》(GB 17740—1999)国家标准,规定了用于测定我国境内发生地震震级的量规函数.王丽艳等(2016)依据大量观测资料重新测定了区域量规函数,应用于国家标准《地震震级的规定》(GB 17740—2017).中国国家标准(GB 17740—2017)重新规定了测量地方性震级时采用的五大分区量规函数,分别是东北与华北、华南、西南、青藏和新疆地区的量规函数,目前中国地震台网中心所采用的正是这一标准.

近年来,与页岩气和干热岩开发有关的诱发地震已成为全球研究热点.作为我国页岩气开发的重点地区,川南地区的历史背景地震活动性较弱,1970年前4级以上地震较少发生(何登发等,2019),1970—2008年上罗镇页岩气开采区也仅记录到60次ML>2.5地震(Lei et al.,2017),自2011年以来,该地区中小微地震数量急剧增加,长宁、筠连、兴文、珙县等多地发生了一系列破坏性地震(易桂喜等,2019;Lei et al.,2019,2020)(图1a).开展小微地震监测,准确测量小微地震的空间位置和震级大小,是评估、控制、降低工业活动触发构造地震风险的首要环节.目前国家标准使用的地方性震级量规函数震中距最小步长为5 km,已不能满足区域地震台网监测到的震中距在数公里范围内的小微地震地方性震级的测定精度要求(Yang et al.,2021).

中国地震局地球物理研究所承担了“川南国家级页岩气示范区地震活动性风险评估与对策研究”项目,自2021年4月起,在长宁—昭通页岩气示范区内布设了107个台站(图1b),监测长宁—昭通一带的小微地震活动.我们基于LOCFLOW流程,对流动台阵记录到的2021年的连续观测数据,开展微震检测、识别与定位,编制了基于LOCFLOW的地震目录(Tian, 2023).相较于中国地震台网中心发布的地震目录,LOCFLOW采用Hutton和Boore(1987)给出的美国南加州地方性震级公式测量震级,其量规函数可能并不适用于本研究区域,因此两个目录给出的震级存在明显的系统偏差(图2b).长宁—昭通页岩气示范区宽频带密集台阵记录的小微地震的震中距普遍在20 km以内,震源深度主要集中在10 km以浅.国家标准规定的量规函数是关于震中距的分段函数,一般适用于台间距较大的固定台站记录的浅源地震,并不适合研究区流动台阵记录的近场小微地震.现行国家标准规定的最小5 km步长的量规函数,按照0～5 km、0～10 km、0～15 km、0～20 km的震中距分档,每档采用相同的校正量对震中距变化在5 km范围内的台站记录振幅进行校正,对于构造复杂的盆地地区,不能准确补偿地震波振幅在数十米到千米尺度的空间变化,尤其是不能较好地对事件附近台站记录的振幅进行校正.

以往的研究中,国内的地方性震级校正方法大多采用参考震级校正方法(项月文等,2018;康清清等,2019;Yang et al.,2021),即以中国地震台网中心发布震级为参考,根据不同地区的衰减特征,分别获得不同地区的量规函数.本文基于参考震级校正和考虑台基校正的量规函数参数拟合反演两种方法,建立了针对长宁—昭通页岩气示范区的地方性震级公式.参考震级校正量规函数参数拟合反演方法以中国地震台网中心根据国家震级测量标准测定并发布的事件震级为参考,从事件目录中选取被研究区流动台阵记录到的所有事件波形数据并测量振幅,在最小二乘意义下极小化根据量规函数计算的震级与参考震级之间的误差,拟合获得研究区的量规函数,从而测定被区域测震台网遗漏但被流动台阵检测到的小微地震震级.考虑台基校正的量规函数参数拟合反演方法则根据多个台站记录到的地震事件的振幅,直接反演获得量规函数参数、震级、台站校正因子、里克特震级标定常数.通过对较小震中距范围的小微地震进行震源距校正,获得了适用于研究区小微地震的地方性震级,为地震活动性和地震风险评估提供更准确的震级.

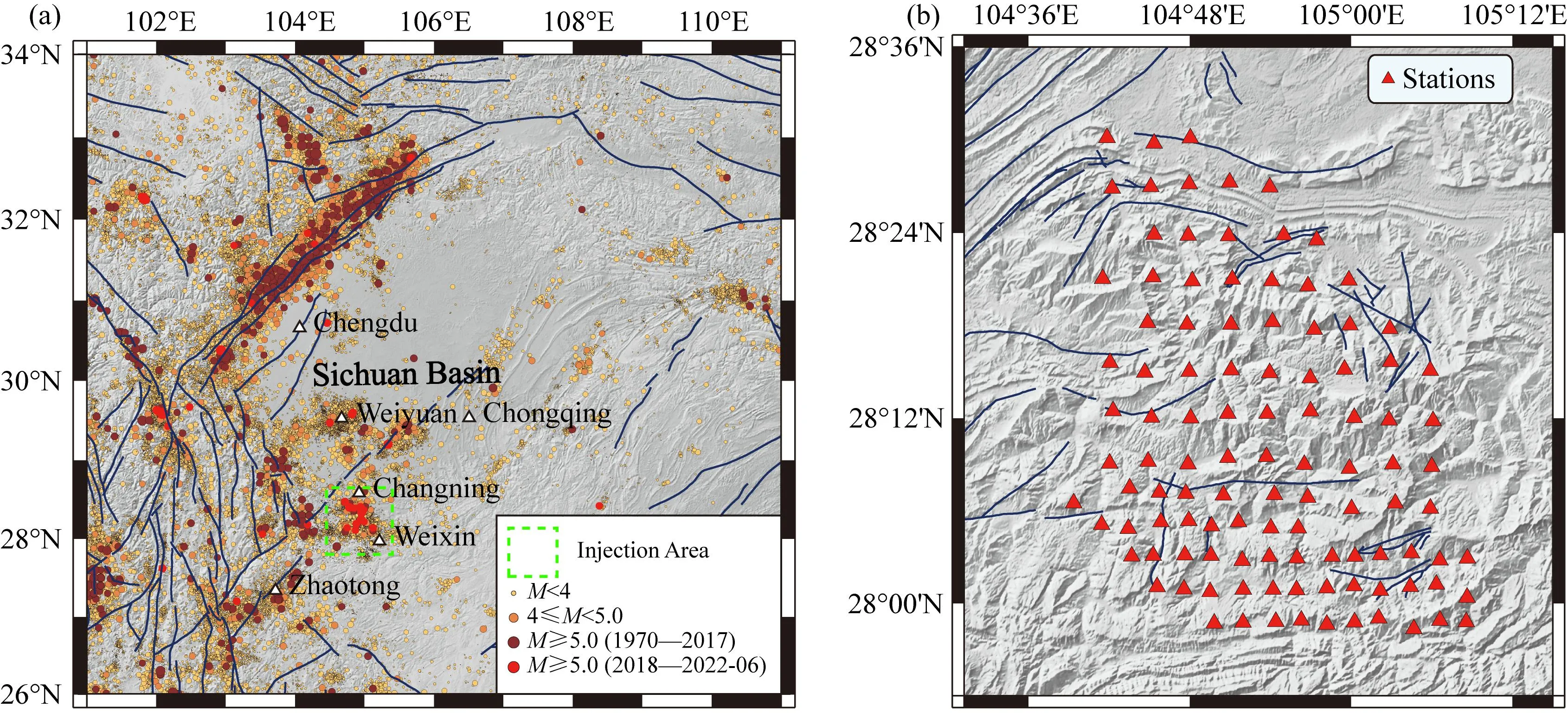
图1 四川盆地及邻区地震活动性及地震台站分布(a) 1970年以来四川盆地及周边发生的地震. 蓝色实线和绿色方框分别代表断层和研究区域,深红色、橘色和黄色的圆点分别表示1970—2017年期间发生的5级以上、4～5级和小于4级的地震,红色圆点表示2018—2022年6月期间发生的5级以上地震; (b) 长宁—昭通页岩气田的地震台站分布. 红色三角和蓝色实线分别代表台站和断层.

1 研究数据

本研究的观测数据来自在长宁—昭通地区布设的107套宽频带地震仪、2021年4月29日—10月29日记录的地震事件数据,台阵采用了CMG-3ESP地震计,装备了Reftek130B数据采集器.台站跨度约60 km,平均台间距约为5 km,覆盖了长宁背斜和建武向斜等小微地震密集区,为我们研究川南地区的地震活动提供了良好的数据基础.

对密集台阵的连续数据采用研究区的一维速度模型,应用LOCFLOW流程检测地震及定位(Zhang et al.,2022).其中,PhaseNet用于拾取震相到时(Zhu and Beroza,2019),HYPOINVERSE 用于绝对定位(Klein,2002),HypoDD用于相对定位(Waldhauser,2001).经质量控制后得到108727个地震事件,获得了长宁—昭通地区地震的精定位目录.震中距分布在0～50 km,震源深度集中在0～10 km,震级集中在0～3级,最大震级5.2级,也就是2021年9月3日发生在建武向斜南翼的MS4.7珙县地震(Tian, 2023).LOCFLOW中使用的震级公式为(Hutton and Boore,1987)：

ML=log10A+1.11log10Δ+0.00189Δ-2.09,

(1)

其中,A为转换到Wood-Anderson仪器记录位移的水平分量最大振幅算术平均值,单位为μm;Δ为震中距,单位为km.

2 研究方法

2.1 我国地方性震级计算国家标准

里克特1935年提出地方性震级概念使用的仪器为Wood-Anderson地震仪,定义震中距100 km记录的1 mm振幅对应于ML=3.0的地震.20世纪50年代中期我国地震台并没有安装Wood-Anderson标准地震仪,因此里克特提出的震级标度不能直接用于我国地方性震级的测定.

1959年,李善邦根据华北地区的地震波衰减规律,得到了一套适用于我国的震级测定方法(李善邦,1981),定义为：

ML=log10Aμ+R(Δ),

(2)

(3)

其中Aμ是以μm为单位的位移振幅峰值,R(Δ)是以震中距Δ标定的量规函数.AN,AE分别为南北向和东西向S波(或Lg波)最大振幅.不同地区地震波的衰减特性不同,因此ML具有明显的地方性特征.

ML使用S波(或Lg波)的最大振幅测定,一个地震事件的地方性震级是各个台站测量到的震级的算术平均值.根据中国地震震级国家标准(GB 17740—2017),震级计算前应将地震记录模拟为DD-1型地震仪的短周期位移记录,并且最大振幅应大于噪声水平的两倍(中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会,2017),然后再根据对应的量规函数,按照公式(2)计算震级(Dai and An,2020).

公式(2)的量规函数R(Δ)描述了地震波随震中距离的衰减特性,其衰减特性与传播路径密切相关(陈培善和秦嘉政,1983;薛志照,1992).GB 17740—2017将中国大陆分为五个区域,这五个区域分别以5 km的震中距为间隔定义了震中距介于0～1000 km范围各自的分区量规函数.黑龙江、吉林、辽宁、内蒙古、北京、天津、河北、山西、山东、河南、宁夏、陕西使用R11,福建、广东、广西、海南、江苏、上海、浙江、江西、湖南、湖北、安徽使用R12,云南、四川、重庆、贵州使用R13,青海、西藏、甘肃使用R14,新疆使用R15.位于四川南部的长宁—昭通页岩气田的密集台阵记录的小微地震震中距鲜有超过60 km,对应的量规函数R13列于表1.据图2a,本研究选取的小微地震震中距连续分布在0～50 km,图2b所示的LOCFLOW测定的小微地震震级与中国地震台网中心(CENC)发布的震级存在明显的系统偏差,两者之间的系统偏差表明现行国家标准规定的量规函数所采用的最小步长为5 km,可能不能准确反映小于5 km的振幅衰减特征以及台站场地特征.

表1 国家标准(GB 17740—2017)规定的四川地区的地方性震级量规函数R13Table 1 The local earthquake magnitude gauge function R13 applicable to the Sichuan region specified in the Chinese National Standard (GB 17740—2017)

2.2 基于参考震级校正的参数拟合反演方法

参考震级校正参数拟合反演方法的基本原理是,以中国地震台网中心提供的震级为约束,利用最小二乘拟合,最小化量规函数震级公式计算的震级与中国地震台网中心参考震级的误差平方和,反演获得能使计算震级接近参考震级的量规函数公式参数,给出参考震级校正公式,基于参考震级公式测定的震级在数值上接近中国地震台网中心测定的震级.

本文采用Havskov和 Ottemöller(2010)定义的地方性震级ML测量公式：

ML=log10A(D)+Qd(D),

(4)

其中,Qd(D)是位移校正项,即量规函数,A(D)是位移振幅峰值,表示为以 km为单位的震源距D的函数：

(5)

其中,A0是震源处初始振幅,β是几何扩展因子,v是S波速度,Q是质量因子.这些参数很难直接确定,因此我们通过构建目标函数,利用最小二乘拟合的方法,求取震级公式的拟合参数,从而免去计算式(5)中不便求取的A0,β,v和Q.

图2 震中距分布直方图、LOCFLOW震级和中国地震台网中心震级对比(a)研究区地震事件震中距步长分别为5 km(左)和1 km(右)的直方图;(b)相同地震事件LOCFLOW测定的震级(蓝色圆点)和中国地震台网中心发布的震级(红色圆点).

为了获得形似式(4)的公式,我们对公式(5)的两边取以10为底的对数得到：

(6)

则式(4)中的衰减项Qd(D)可以表示为：

(7)

将公式(7)代入公式(4),假设所有射线路径的v,Q和f不变,地方性震级ML便可以写成：

ML=log10A+m1log10D+m2D+m3,

(8)

其中,常数m1,m2,m3分别表示几何扩展因子、几何衰减因子和基准水平.

地震事件i在台站j测得的地方性震级可以表示成：

Mij=log10Aij+m1log10Dij+m2Dij+m3,

(9)

地震事件i的震级由多个台站测得的震级Mij的平均值得到：

(10)

其中Ns为记录地震事件i的台站数量.

设立目标函数F(m1,m2,m3),使目标函数最小,通过最小化量规函数预测震级与台网参考震级之间的差值平方和,反演获得公式(9)中的系数.

(11)

参考震级校正方法的具体步骤如下：

(2)对地震波形进行预处理,去均值,去除仪器响应,转换成Wood-Anderson仪器的位移;

(3)计算每个Wood-Anderson位移水平分量最大振幅的算术平均值Aij;

(4)通过最小化目标函数F求解式(11)的拟合参数m1,m2,m3;

(5)将拟合参数m1,m2,m3代入式(9)和式(10),获得每个事件的震级Mi.

通过与中国地震台网中心的地震编目的比对,以台网中心测定的震级为参考,本文从川南工业区流动地震台网定位获得的地震目录中,选取290个事件,将台阵记录的波形数据去除仪器响应并转换到Wood-Anderson仪器的位移记录,单位为μm.然后,在每个事件波形S波前后20 s的窗口内,计算两个水平分量峰值AN,AE的算术平均值作为位移振幅峰值Aij,如图3所示.

图3 水平分量最大振幅截取窗口(红色部分)

图5 参考震级校正方法的拟合结果(a)和(b)分别为北区拟合结果和南区拟合结果.横纵坐标分别为参考震级校正得到的震级和台网中心发布震级.

我们将研究区分成南北两个分区分别拟合震级公式,其中北区以长宁背斜为主,南区以建武向斜为主,事件分布如图4所示.在北区和南区的参考事件个数分别为108次和182次,拟合后获得的震级公式分别为公式(12)和(13),拟合结果如图5所示,从拟合结果看,南区拟合的震级更接近国家台网中心测定的震级水平.

ML=log10A-2.89log10D+0.02D+1.289,

(12)

ML=log10A-1.88log10D-0.03D+0.897.

(13)

将上述公式应用于南北两个分区未被区域台网记录的小微地震,即可得到与国家震级测量标准基本一致的小微地震震级.

2.3 考虑台基校正的参数拟合反演方法

考虑台基校正的参数拟合反演方法的基本原理是利用大量地震事件在多个台站记录的地震波形的振幅数据及震源距,根据量规函数公式反演获得相关的拟合参数与震级,并校正到里克特震级标准.不同于参考震级校正方法,台基校正方法采用里克特震级作为参考标准,计算转换到Wood-Anderson仪器响应的位移最大振幅和震源距,构造矩阵方程,利用奇异值分解反演得到与震源距有关的振幅校正参数、震级、台站校正项以及里克特震级标定常数,其中的台站校正项考虑了台站场地条件对地震波振幅的影响.里克特震级标定常数,也就是所谓的基准水平,则将震级校正到里克特标准.

Bakun和Joyner(1984)建立了适用于美国加利福尼亚中部地震的ML震级标度,采用的震级测量公式为：

ML=log10A+alog10R+bR+S+c,

(14)

其中,A定义为Wood-Anderson地震仪在震中距Δ测得的最大振幅,震中距和振幅的单位分别为km和nm,本文采用震源距R替代震中距,a和b分别表示振幅与几何扩散以及衰减有关的常数因子,S为台站校正项,c为根据里克特地方震级定义确定的震级校准常数,即将震中距100 km处Wood-Anderson仪器记录振幅1 mm、相当于481 nm实际位移的地震震级标定为ML=3.0(Richter,1935),本文称之为里克特震级标定常数.

研究表明,地方性震级测量须考虑地震波振幅随震中距衰减的区域变化特征(Alsaker et al.,1991;Kim, 1998;Keir et al.,2006;Saunders et al.,2012;Ottemöller and Sargeant,2013;Li et al.,2015).为了获得区域性的ML测量公式,一般基于区域内不同震中距范围内足够数量的观测数据,通过求解以下方程组,反演获得拟合参数：

-log10Aij=alog10Rij+bRij-MLi+Sj+c,

(15)

其中,i和j分别为地震事件和台站,MLi是事件i的平均震级,Sj是台站j的台站校正项,所有台站校正项的总和为0,故台站校正项是相对校正量.本研究采用奇异值分解反演该线性系统,求取a,b,MLi和Sj(Teukolsky et al.,1992;Ottemöller and Sargeant,2013;Menke,2018).构造如下的线性方程组：

(16)

其中m和n分别是反演所用到的地震事件数量和台站数量.

关于里克特震级标定常数c,大多数地方性震级测量均采用里克特震级定义,确定适用于不同区域的校正基准量.Hutton和Boore(1987)在编制美国南加州地区的量规函数时,建议采用震中距17 km 振幅10 mm对应ML=3.0作为标准,测量南加州地震的地方性震级.

采用与参考震级校正方法相同的分区,我们利用考虑台基校正的参数反演方法分别拟合北区和南区的震级测定公式,为对比两个分区独立反演获得的台站校正项,两个分区均使用所有107个台站的记录.考虑到矩阵方程未知数的数量,为保证反演结果的准确性,只使用被4个以上台站记录的地震事件,通过奇异值分解反演和里克特震级校正,分别获得南北两个分区的震级测量公式.

在北区共筛选了2595次地震事件,得到震级公式如下：

ML=log10A+1.115log10D+0.0015D

-2.063+Sj;

(17)

在南区共筛选了1332次地震事件,得到的震级公式如下：

ML=log10A+1.104log10D+0.0023D

-2.121+Sj.

(18)

反演获得北区与南区震级大小与每个台站的台站校正项如图6所示,参与反演的台站分布如图7所示,北区和南区独立反演获得的台站校正项之间的相关性如图8所示.

由于研究区地震事件的震中距均在60 km以内,缺失里克特震级定义的100 km附近的地震事件,故我们根据公式(17)和公式(18)的结果取平均值,定义震源距为6 km 振幅10 mm对应ML=3.0,作为川南地区的震级参考标准.

为对比台站分布范围对震级测定的影响,我们分别选取南北分区内部的台站,北区共筛选了1264次地震事件和25个台站,南区共筛选了1328次地震事件和82个台站,得到了基于分区内部台站数据获得的震级公式,北区和南区的震级计算公式分别为公式(19)和(20).北区与南区震级大小ML与各台站的台站校正项Sj结果如图9所示.

ML=log10A+1.118log10D+0.0019D

-2.109+Sj,

(19)

ML=log10A+1.125log10D+0.0026D

-2.193+Sj.

(20)

将上述公式应用于南北两个分区所有小微地震,即可得到与里克特震级标准基本一致的小微地震震级.

3 数据分析与结果讨论

参考震级校正和台基校正两种震级测量方法获得的小微地震震级对比如图10所示,不难发现,在整个研究区域,参考震级方法测得的小于1.5级与台基校正方法测得的小于1级的震级分布相关性较弱,在此水平之上的绝大多数地震的震级则存在明显的线性关系.

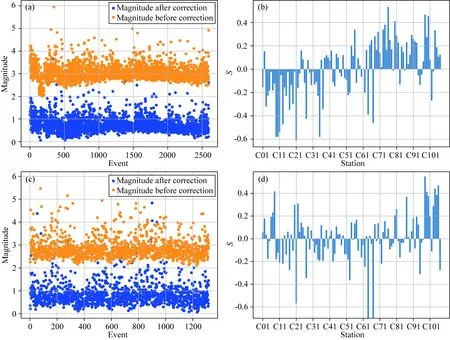
图6 台基校正方法的拟合结果,南北分区均使用全部台站(a)和(b)分别为北区2529次地震事件、107个台站反演得到的震级与台站校正项;(c)和(d)分别为南区1332次地震事件、107个台站反演得到的震级与台站校正项.橙色圆点和蓝色圆点分别表示奇异值分解后得到的震级和校正到里克特震级标准的震级.

图7 北区和南区独立反演获得的台站校正项(a)和(b)分别表示北区和南区地震事件独立反演获得的台站校正项.

图8 北区和南区独立反演获得的台站校正项之间的相关性

基于本文两种震级测量方法以及LOCFLOW内置算法获得的南北两个分区的地震震级,我们计算获得了南北两个分区的震级-频度关系式,南北两个分区的b值和震级分布如图11所示.

结果显示,LOCFLOW、参考震级校正和台基校正方法获得的北区完备震级Mc分别为0.6、0.8和0.6,b值依次为1.16、1.48和1.06.在南区,所对应的完备震级Mc分别为0.5、0.9和0.6,b值依次为1.12、1.32和1.06.

根据参考震级校正方法获得的b值与另外两种方法获得的b值差距较大,且地震目录完备性也低于后两种方法,可能是因为使用的位移数据是Wood-Anderson仪器仿真记录,而非国家标准规定的DD-1仪器记录,我们将在后续研究中开展深入分析.地方性震级宜通过考虑台基校正的参数拟合反演方法获得的量规函数直接测量,慎用以国家台网发布震级为参考震级,通过构建Wood-Anderson仪器仿真数据的量规函数的方法间接测量.

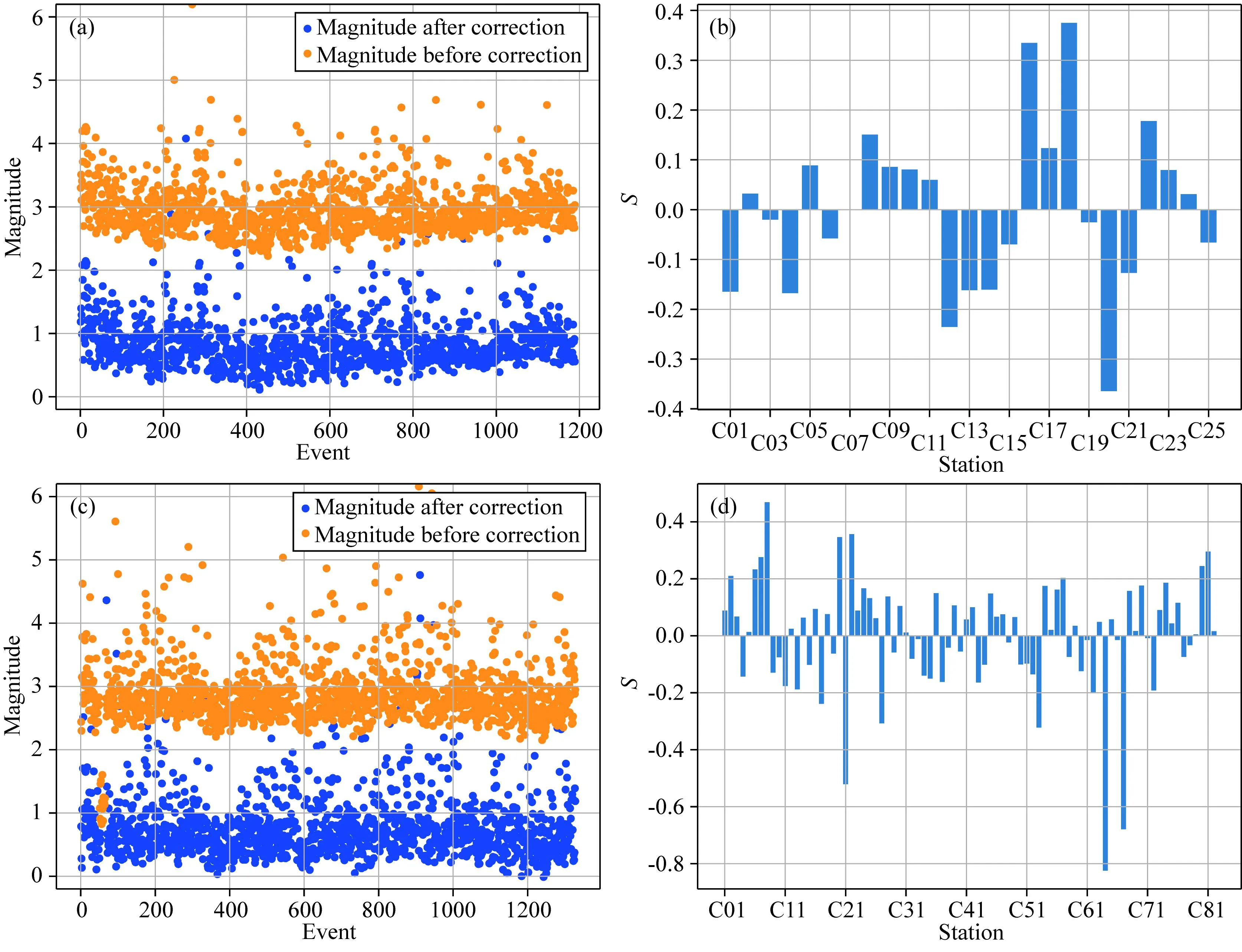
图9 台基校正方法的拟合结果,南北分区分别使用位于分区内部的台站(a)和(b)分别为北区1264次地震事件、25个台站反演得到的震级与台站校正项;(c)和(d)分别为南区1328次地震事件、82个台站反演得到的震级与台站校正项.橙色圆点和蓝色圆点分别表示奇异值分解后得到的震级和校正到里克特震级标准的震级.

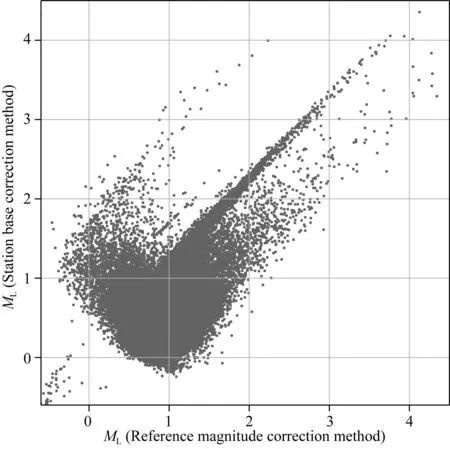
图10 基于参考震级校正方法和台基校正方法获得的震级对比

4 结论

本文使用参考震级校正和基于台基校正的参数拟合两种方法,用震源距替代震中距,针对长宁—昭通页岩气示范区内北区和南区,分别获得了小微地震的地方性震级测算公式,并将其应用于2021年4月至10月密集台阵的地震记录.两种方法都具有一定的参考价值,利用参考震级校正方法可以将密集台阵记录的地方性震级校正到与现行国家标准一致,利用台基校正方法可以将密集台阵记录的地方性震级校正到与经典的里克特震级标准一致.

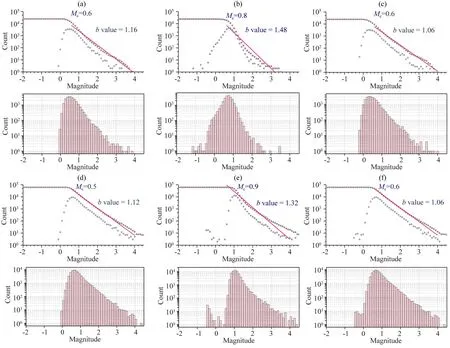
图11 基于三种方法获得的震级-频度关系(a)(b)(c)北区; (d)(e)(f)南区.从左到右依次为LOWFLOW流程、参考震级校正方法、台基校正方法.

在参考震级校正方法中,我们根据流动台阵检测到的地震事件目录,从国家台网中心地震编目中选取了290个被流动台阵检测到的地震事件作为参考事件,采用最小二乘拟合反演方法,确定了适用于长宁—昭通页岩气示范区的震级测算公式的最佳拟合系数,建立了基于参考震级的区域性量规函数.在台基校正方法中,我们利用众多台站记录到的大量地震事件的振幅和震源距数据,构造矩阵方程,反演获得了包括台站校正项在内的量规函数参数以及震级,并确定了里克特震级标定常数,相比参考震级校正方法,该方法考虑了不同台站场地条件对振幅的影响,且无需挑选参考震级作为约束,适用于缺少参考震级约束的小微地震震级测定.我们将震源距为6 km 振幅10 mm对应ML=3.0,作为川南地区的震级参考标准.

我们利用参考震级校正和考虑台基校正的参数拟合反演方法测定的震级,分别获得了研究区南北分区的b值和完备震级Mc,结果对比表明,台基校正参数拟合反演方法测定的震级所获得的b值和完备震级Mc与LOCFLOW流程更为接近,基于参考震级拟合反演方法所得结果与LOCFLOW流程、台基校正参数拟合反演方法存在明显不同,可能是因为本研究使用的位移记录是转换到Wood-Anderson仪器响应的位移,而国家震级测量标准则采用DD-1仪器响应的位移.建议小微地震震级测定采用考虑台基校正的参数拟合反演方法,构建区域性的量规函数,直接测量地方性震级.

致谢谨以此文祝贺滕吉文先生90华诞暨从事地球物理工作70年.感谢中国地震台网中心、国家地震科学数据中心(http：∥data.earthquake.cn)提供数据支撑.感谢长宁—昭通页岩气示范区的台阵布设人员的野外工作以及数据处理.本文图件主要由 GMT(Wessel et al.,2013)程序完成.