基于最小二乘法的新能源出力时序数据重构方法

李锐锋，周 刚，凌汝晨，操晨润，蔡淼中

(国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314000)

0 引言

发展和推动清洁能源消纳，是调整能源结构、节能减排、合理控制能源消费总量、实现能源可持续发展、转变经济发展方式的必然选择。我国清洁能源资源丰富，分布广泛，发展清洁能源对我国能源安全、节能减排和可持续发展都有着重大的战略意义。

风力、光等清洁能源发电具有很强的随机性和波动性，因此，如何实现大规模的消纳是一个全球性的问题。由于我国的资源特性、电力系统条件、电力市场机制等原因，使得消纳清洁能源的任务更加艰巨。随着大规模的清洁能源开发，部分区域消纳矛盾日益突出，导致了风能、光伏的弃用等问题。下面提出时序数据重构方法，为解决我国新能源消纳问题提供对策和方法。

1 新能源出力特性

1.1 风电出力特性

风能是风力发电的能源来源，风电的出力特性与风场的特点有很大关系。由于自然风的强度和方向无时无刻不在变化，具有一定的随机性和间断性，所以风力发电机或风电场的输出功率也会随着季节、时段的变化而产生一定的波动。

一般情况下，一个大型风电场由数十、数百、甚至数千个风力发电机组组成，由于风电场面积、场地地形、机组排列方式等原因，每个机组会有不同的风速，从而造成不同的机组输出功率。一般而言，风机间距愈大，两台风机间的风速关联度愈低，说明两台风机间的风速差异愈大，其输出功率间的互补性愈强。在相同的时间尺度上，随着机组数目的增加，以及空间分布规模的增大，风力发电功率的变化幅度逐渐减弱，并呈现出明显的聚合效应。

风力发电机组的出力与风速有直接关系，其输出功率与风速呈非线性关系，用来描述二者关系的曲线叫做风机功率特性曲线，其形式和表达方式多种多样。图1 是一种典型的风机功率特性曲线。其输出功率可按式(1)计算。

图1 典型风机功率特性曲线(非线性)

当采用近似线性特征进行等效时，可以将风机的输出功率特征用分段函数表达为：

式(1)～(5)中，Pr为风电机组额定出力，vr为额定风速，vci为风机切入风速，vco为切出风速，v为风力发电机组轮毂高度上的风速。

风机线性功率特性曲线如图2 所示。

图2 风机线性功率特性曲线

1.2 光伏发电出力特性

光伏发电的周期性、随机性和间断性是由于受到季节、日夜、气候和天气等因素的影响。从年度来看，夏季太阳辐照强度较大，光伏电站出力较大；冬季太阳辐射强度较小，光伏电站出力较小。总体来说，5—7 月是一年当中太阳辐照最强的三个月，此后逐渐减小，到12 月降到全年最低。从一天来看，上午随着太阳时角的增大，太阳辐照强度逐渐增大，直至正午增加到最大，下午逐渐减小。晴天时，邻近日之间光伏电站日发电量和出力曲线存在显著的相关关系，规律性强；在多云和阴雨天气条件下，邻近日之间的光伏出力曲线存在很大的差别。当太阳被快速通过的云团频繁遮挡时，光伏出力表现出很强的随机波动性。

描述光伏电站输出波动特性的典型方法包括1 min 变化量、10 min 变化量及1 h 变化量。一般来说，时间间隔越长，引起的输出变化量越大。

国家电网有限公司光伏发电相关规定指出，在光伏发电站并网以及太阳辐照强度增大过程中，光伏发电站有功功率变化应满足电力系统安全稳定运行的要求，其约束条件取决于接入电网的调频特征，应该由电网调度控制部门确定。光伏发电站有功功率变化限制可参考表1，该要求也适用于光伏发电站的正常停机。允许出现太阳辐照强度降低而引起的光伏发电站有功功率变化超出有功功率变化最大限值的情况。

表1 光伏发电站有功功率变化限制

由于太阳光的特性，很大区域内太阳光几乎同时到达，光伏电站输出在相当分散的地理位置上往往具有高度的相关性，天气晴好时通过地理分散来减小整体输出的波动性不如风电场明显。但在多变天气条件下由于不同区域太阳辐照变化较大，大型光伏电站输出具有一定的平滑作用。

2 新能源发电出力的相关性

2.1 光伏电站出力相关性量化分析

以某西部省份A 光伏电站和B 光伏电站为例。光伏发电站出力相关性以皮尔逊(Pearson)相关系数作为量化指标，显著性检验水平α=0.01，对两个光伏电站在不同时段(日、周、月、年)的相关性进行分析，计算其不同时间尺度内的相关性指标(表2～5)。

表2 光伏电站日出力相关性

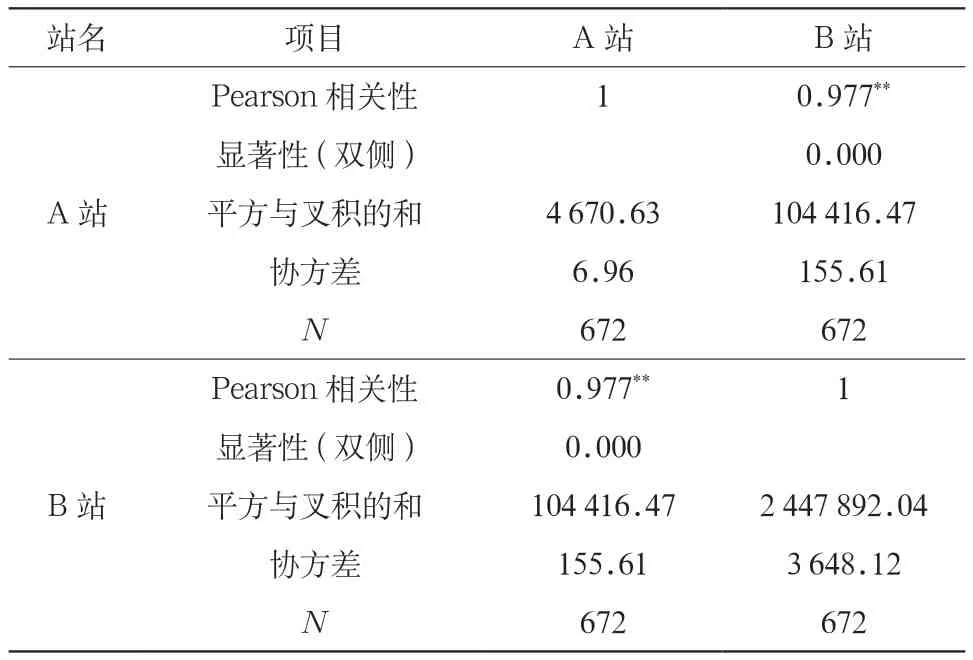
表3 光伏电站周出力相关性

表4 光伏电站月出力相关性

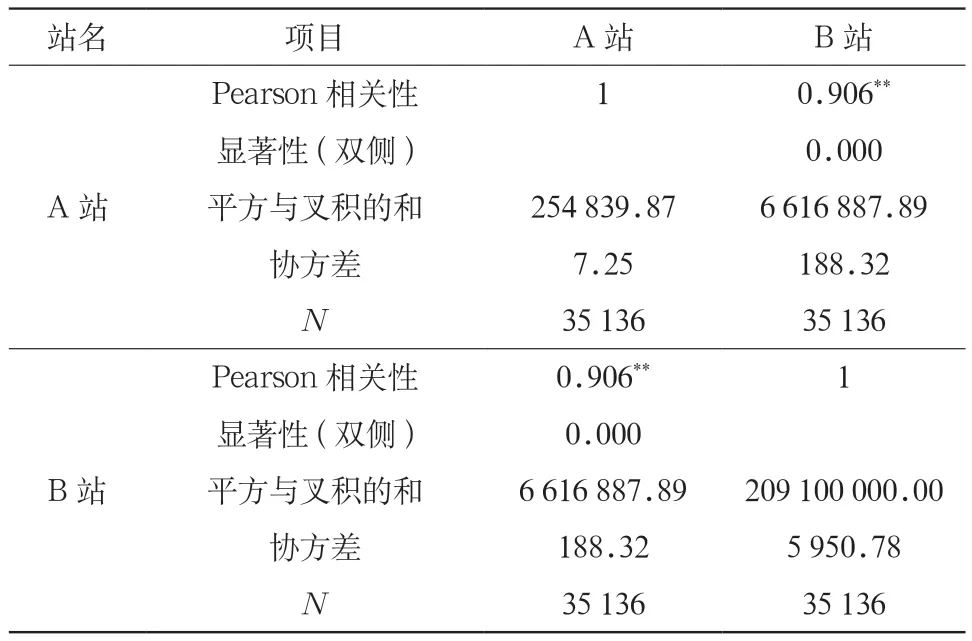
表5 光伏电站年出力相关性

2.2 风电场出力相关性量化分析

以某西北部地区C 风电场和D 风电场为例，风电场出力相关性以皮尔逊(Pearson)相关系数作为量化指标，显著性检验水平α=0.01，对两个风电场在不同时段(日、周、月、年)的相关性进行分析，计算其不同时间尺度内的相关性指标(表6 ～9)。

表6 风电场日出力相关性

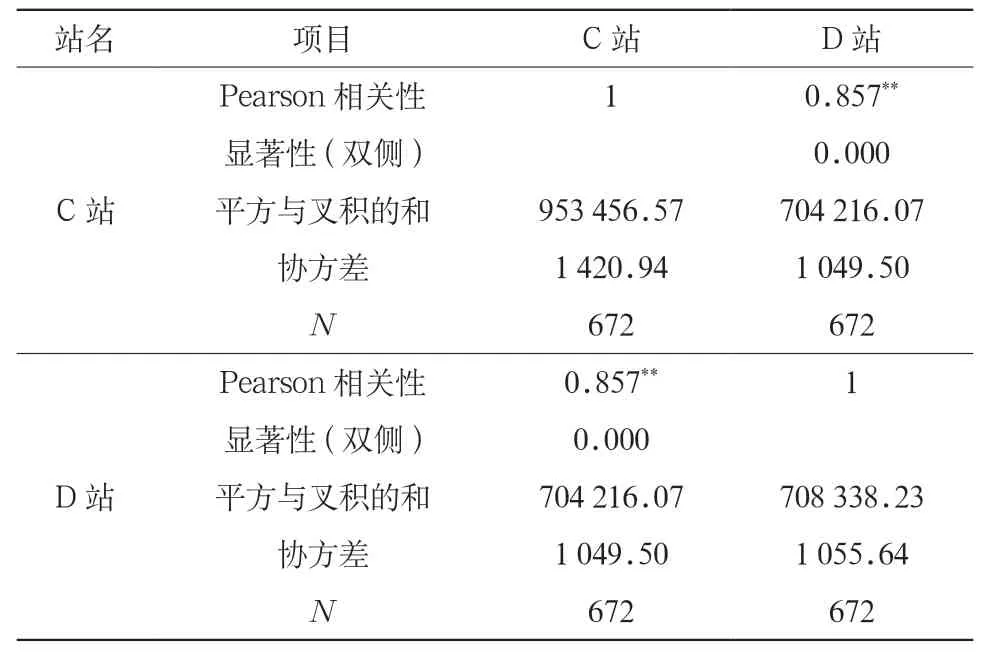
表7 风电场周出力相关性

表8 风电场月出力相关性

表9 风电场年出力相关性

3 新能源出力概率模型

3.1 风电出力概率模型

有许多模型用于模拟风速的概率分布，例如韦布尔(Weibull)分布、瑞利(Rayleigh)分布等，两参量的Weibull 分布是目前应用最广的模型。假定风场的风速序列采用两参量Weibull 分布，其分布函数和概率密度函数为：

式(6)～(7)中，c是Weibull 分布的尺度参数，k是Weibull 分布的形状参数，v是指风电场风速，V是指定的风速，其中c可以体现风电场的平均风速，k需通过参数估算法求出。

当c=10.531 2，k=1.920 0 时，Weibull 分布概率密度曲线如图3 所示。

图3 Weibull 分布概率密度曲线1

当c=7.654 2，k=2.371 8 时，Weibull 分布概率密度曲线如图4 所示。

图4 Weibull 分布概率密度曲线2

3.2 光伏出力概率模型

光伏系统的输出功率取决于太阳辐照强度、光伏阵列面积和光电转换效率。在350～1 000 W/m2的辐照强度下，太阳能电池的输出功率与其辐照强度成正相关。整个光伏发电系统的输出功率为：

其中，r表示太阳辐照强度，A表示光伏阵列面积，ρ表示光电转换效率。通常，最常用的太阳辐照强度都是服从贝塔(Beta)分布，其概率密度函数如下：

其中，r表示太阳辐照强度，rmax表示最大太阳辐照强度值，α、β表示Beta 分布的形状参数。在Beta 分布中，α、β的改变会使Beta 分布曲线的形状发生改变。

在同一个区域内，有许多因素会对太阳辐照强度产生影响，而气象条件是一个重要的因素。在不同气象条件下，其太阳辐照强度的概率密度函数所用的参量是不同的。

将现有的光伏发电功率输出公式与太阳辐照强度概率函数相结合，得到光伏发电功率输出的概率密度函数如下：

其中，Pmax表示光伏出力的最大值，可以利用下式求得：

因此，光伏出力也服从Beta 分布，相应气象条件下的太阳辐照强度概率密度函数的形状参数用参量估算法求出。

当α=3.986 4，β=7.404 2 时，Beta 分布概率密度曲线如图5 所示。

图5 Beta 分布概率密度曲线

4 新能源出力时序数据重构

4.1 参数估计方法——最小二乘法

最小二乘法是最常用的参数估计方法。下面利用最小二乘法对两个参量进行参数估计。

在几何上，求取与给定点(xi，yi)的距离平方和最小的曲线y=p(x)，而求拟合函数或最小二乘解p(x) 的方法叫做曲线拟合的最小二乘法。

4.2 新能源出力数据重构步骤

由于风电、光伏出力的概率分布服从典型概率模型(Weibull 分布、Beta 分布等)，因此基于典型出力时序曲线，采用参数估计方法，可以得到该场景下的新能源出力的概率模型参数，进而得到对应的出力概率模型。最后根据概率模型进行抽样实现出力数据的重构。具体流程如图6 所示。

图6 新能源时序出力数据重构流程

5 结论

风能和光伏是我国常见的清洁能源。以上在分析风电出力和光伏发电出力的基础上，结合实际案例对风电和光伏发电的出力相关性进行了量化分析，进而得到新能源出力的概率模型，风电出力服从Weibull 分布，光伏出力服从Beta 分布。基于最小二乘法提出新能源出力时序数据重构步骤，为新能源合理利用和并网优化提供指导。