基于化学反应动力学的氨-氢混合无碳燃料燃烧爆炸机理研究

滕霖，单志伟，李西贵，李卫东，罗宇，江莉龙

福州大学化工学院，福州 350108

0 引言

氨（NH3）被认为是世界未来经济的重要资源，其应用涉及能源行业、运输业、制冷业、农业以及其他行业［1］。氨成为国际低碳替代燃料的选择和可再生氢（H2）的载体［2］，氢也被视为最有潜力的可替代燃料、无碳燃料［3］。Khatee 等［4］得出氨-氢空气混合物具有稳定的火焰和较低的一氧化氮排放量，具有作为燃料的巨大潜力，但是氨、氢的能量密度均较高，具有易泄漏、爆炸范围广（氢气的爆炸极限为4.1% ～ 74.1%、氨气的爆炸极限为15.5% ～27.7%）、点火能量低（其中氢气仅为0.017 MJ）、火焰传播速度快等问题［5］，所以氨在分解制氢等应用环节一旦遇到意外的点火源，极易在有限的空间内产生爆炸，进而导致严重的人员伤亡和损失［6］。

已有研究对氨-氢混合气体燃烧爆炸机理的研究较为有限［7-8］。早期描述氨燃烧化学的尝试主要集中在氮氧化物（NOx）的形成。受此启发，一些学者［9-13］对包括氨-氢-氧和氨-氧在内的一组预混火焰进行了系统和详细的研究，确定了自由基·NO和·NH2与·N 反应形成N2以及确定·NO 转化路径的重要性，旨在开发与各种燃烧系统相关的可行氨-氢反应机理。

Zhu 等［7］使用了详细的化学反应机理，在充满氨-氢-氧的混合物的二维阻塞通道中模拟了火焰传播和从爆燃转变为爆轰的过程。Li 等［14］研究了氢-氨-空气云爆炸特性，并揭示了火焰行为和最大爆炸压力之间的相关性。Zhou 等［15］证明了向氨-氧混合物中添加微量氢可以定性地将爆炸极限从单调情况改变为非单调情况，并且爆炸极限图像具有多个转折点。Liu 等［16］基于灵敏度和特征值分析方法，研究氨-氢-氧混合物的爆炸极限特性，并构建了高效的氨-氢爆炸极限预测机制。Liang 等［17］研究氨-空气火焰特性和爆炸超压，通过实验获得了火焰行为、层流燃烧速度和超压动力学等特征。

上述对氨-氢气体的研究，均集中在氨-氢燃烧爆炸压力和爆炸极限体系，得到的均为压力方面特性，而关于燃烧爆炸机制的研究屈指可数，造成采用数值模拟计算氨-氢系统燃烧爆炸过程消耗了大量计算资源，无法高效指导氨-氢混合无碳燃料的燃烧过程及爆炸防控。为此，优选出目前已有的详细氨-氢燃烧机理，利用带有误差传播的有向关系图（DRGEP）法与耦合误差传播和敏感性分析的直接关系图（DRGEPSA）法简化详细机理。将简化机理的点火延迟时间和层流火焰速度的模拟值与实验值相比较，验证机理的可行性。进而将简化后化学反应机理与计算流体动力学（CFD）耦合，开展燃烧过程的数值模拟研究。分析在特定爆破压力条件下，简化机理和详细机理的平均激波速度，以期完善对氨-氢混合气体燃烧爆炸机理的认识，推进氨-氢燃烧模拟技术的发展。

1 化学反应动力学

1.1 反应机理优选

对多个氨- 氢燃烧反应机理［18-24］与实验结果［25-29］进行对比研究，以期优选出合适的反应机理（见图1、图2）。在预测点火延迟时间方面，Song等［18］、Tian 等［19］和Klippenstein 等［21-22］的模型普遍低于实验值；Otomo 等［24］和Dagaut 等［20］的模拟值与实验值达到了良好的一致；Mathieu 等［23］改进了Dagaut 等［20］的模型，通过增加关键的基本反应和调整反应速率常数，优化了模型，优化后的模型也能准确预测了点火延迟时间，但在预测氨燃烧火焰速度方面明显高于实验值。在预测层流火焰速度方面，Otomo 等［24］的模拟值与实验值十分吻合，但其他机理均未能准确重现火焰速度的实验结果。因此只有Otomo 等［24］的机理符合需求。

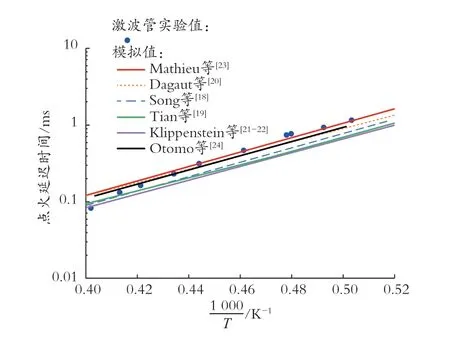
图1 大气压下激波管点火延迟时间实验值与各种机理模拟值的对比关系

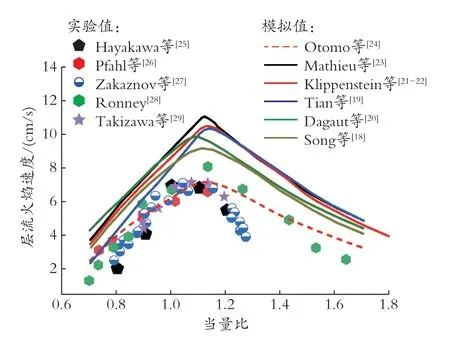
图2 不同当量比下层流火焰速度实验值与各种机理模拟值的对比关系（初始压力为1 atm）

由图1 和图2，点火延迟时间和层流火焰速度在使用Otomo 等［24］的机理得出的模拟值均与实验高度一致。并且Otomo 等［24］基于Song 等［18］的模型，对氨氧化反应机制作出相应改进。在目前的模型（Otomo 机理）中，包括自由基·NH2、·HNO和·N2H2的反应在改进模型中发挥了关键作用。在Otomo 等［24］的研究中，详细机理已被广泛用于实验验证［30-32］和模拟研究［32-34］，所以本次研究基于Otomo 等［24］的机理（包含33 种组分和213 个基元反应），对氨-氢燃烧的详细机理开展进一步简化研究。的表示方法是阿伦尼马斯方程的一个变形，用于描述温度如何影响反应速率。

在机理简化方法方面，Lu 等［35］最初引入了有向关系图（DRG）法，成功地将乙烯机理从70 个物种和463 个反应简化为33 个物种和205 个反应的简化机理。后续Zheng 等［36］融合了误差传播策略，提出了DRGEP 版本。但这些方法仍有缺陷，如DRG法在识别多余反应上存在短板，DRGEP 法因线性耦合会产生误差。为改进上述问题，Niemeyer 等［37］开创了结合误差传播和敏感性分析的DRGEPSA 法，将DRG 法、DRGEP 法、DRGASA 法、DRGEPSA 法这4 种简化方法应用于正庚烷的详细机理分析，对它们的的有效性进行验证，在特定条件下（1 atm、1 000 K、当量比为0.5 ～ 1.5）进行了实验。该复杂机理涉及561 种化合物和2 539 个反应过程，误差限定在0.5% ～ 40%。如图3 所示，DRGEPSA 法在整个误差范围内，能够形成更精简的骨架机理。特别是当误差范围超过20%后，化学反应的数量变化减小，这表明多余反应已被有效剔除，而进一步的剔除可能导致重大影响。DRGEPSA 法因其在移除无效组分和反应时，更精准地保持了关键氧化反应，被认为是一种高效的方法［38-41］。因此，本研究采用DRGEPSA 法来简化机理并实现包括对直接相互作用系数（DIC）的改进定义。这种改进是必要的，因为在涉及快速模式的长化学反应路径的情况下，原始定义存在缺陷［42］。DRGEP 法利用DRG 来描述反应系统中物种耦合的依赖关系，图4 所示展示了DRG中物种之间的典型关系。箭头表示一种物种对另一种物种的依赖方向，宽度表示依赖的强度。因此，对于必须保留的物种A 来说，可以看到物种A 依赖于物种B，但物种B 不依赖于物种A。此外，由于物种B 和物种D 紧密耦合，它们形成了物种A 的依赖集｛B,D｝，必须保留以正确预测物种A。然而，物种C、E、F 可以被消除，因为它们既不被物种A需要，也不被物种A 的依赖集中的任何物种所需。此外，在紧密耦合的群体内，如｛B,D｝和｛E,F｝，物种应该被一起保留或一起消除。

图3 使用DRG、DRGEP、DRGASA 和DRGEPSA 生成正庚烷骨架机理误差限制函数的物种数量

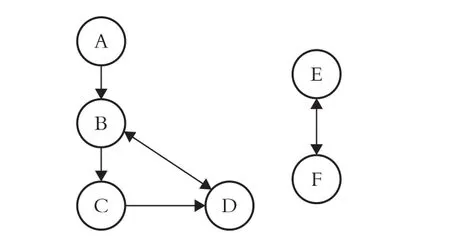
图4 DRG 法物种典型关系示意

为了获取简化机理，首先将详细机理导入CHEMKIN 软件的零维均质模型中，初始条件设定为温度为1 000 K、1 250 K 和1 500 K，当量比为0.5、1 和2，初始压力为9.87 atm、39.48 atm 和59.22 atm，并以点火延迟时间、·H、·OH、·NH2、·HNO 和·N2H2的摩尔分数作为目标参数；设定10%的误差阈值；得到初步简化机理；再通过加入敏感性分析，保留敏感性系数较大的基元反应，并剔除敏感性系数较小的基元反应，得到最终的氨-氢简化机理。考虑到基于氨-氢的化学机制的复杂性，本研究在详细机理的基础上未修改速率系数、温度指数等参数。通过采用DRGEPSA 法去除了详细机理中的冗余反应，最终得到了一个包含19 种组分和100 个基元反应的简化机理。图5 表示氨-氢化学反应机理的简化过程。

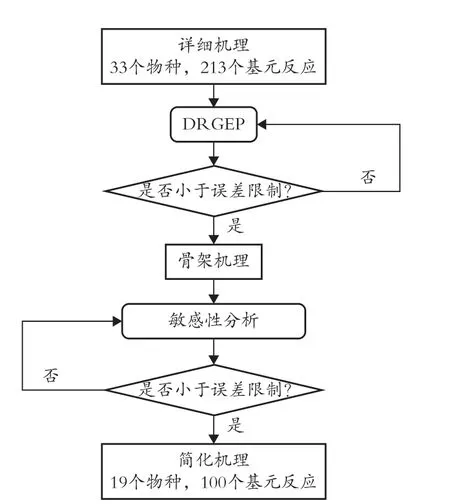
图5 DRGEPSA 机理简化流程

1.2 化学反应动力学验证

点火延迟时间和层流火焰速度对自然燃烧爆炸的影响至关重要［43-44］。点火延迟时间描述混合气体从点燃至燃烧的时间差，关系到爆炸的突发性；层流火焰速度反映火焰在无湍流的情况下的传播快慢，决定燃烧强度［45-46］。以上2 个参数是评估燃烧和爆炸潜在危险性的关键，以下对其进行详细验证和探讨。

1.2.1 点火延迟时间验证

将简化机理在CHEMKIN 中得出的模拟数据与Mathieu 等［23］在激波管上测量得到的氨点火延迟时间的实验数据作为参照。初始条件：当量比为0.5、1.0 和2.0，初始压力为1.4 atm、11.0 atm 和30.0 atm，初始温度为1 500 ～ 2 500 K。图6 表示了详细机理和简化机理的点火延迟时间的数值结果和实验值的对比，可以看出，详细机理和简化机理在氨点火延迟方面均表现良好，而详细机理显示出更高的准确性。当量比为0.5，压力为1.4 atm 时，相较于详细机理，简化机理与实验数据的吻合程度更高；当量比为0.5，压力分别为11 atm 和30 atm 时，在较高的温度下，与详细机理对比，简化机理低估了点火延迟时间，但是和实验值更加吻合，在较低的温度下，与详细机理和实验值对比，简化机理高估了点火延迟时间。这是由于简化机理去掉了部分参与对低温敏感的的组分及基元反应，使得低温下的反应预测较详细机理略微不准确。

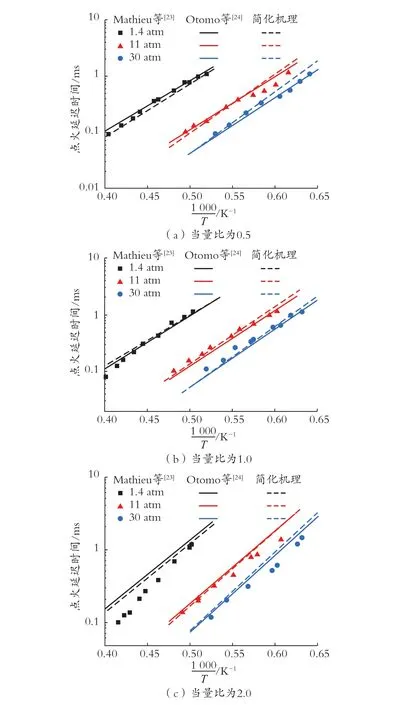
图6 不同当量比下的点火延迟时间验证

1.2.2 层流火焰速度验证

图7 展示了压力为1 atm、3 atm 和5 atm 下的氨-氢-空气混合物的层流火焰速度，经过与实验数据的对比，进一步验证本模型的准确性。结果显示，在不同压力条件下，详细机理和简化机理均能良好地模拟氨-氢的层流火焰速度。在压力为3 atm和5 atm 下，与Song 等［18］、Tian 等［19］机理得出的模拟值相比，简化机理和详细机理模型更加符合实验值。而在压力为1 atm 下，Song 等［18］和Tian 等［19］的机理对实验值的预测比简化机理和详细机理更为准确。因此，可以得出简化机理和详细机理模型在高压条件下能够很好地预测实验值的结论。在H2占比较小时（摩尔分数小于0.2），详细机理和简化机理比Song 等［18］和Tian 等［19］之前的模型更加符合Ichikawa 等［47］在3 atm 和5 atm 下的实验值，但是详细机理比简化机理更接近实验值。在H2摩尔分数较高区域，本模型和之前的模型之间的差异较小，这是由于氨-氢-空气混合物中以H2燃烧为主导。值得注意的是，与详细机理相比，简化机理与实验值的吻合程度更好。

图7 氨-氢-空气混合物层流火焰速度验证

1.2.3 基元反应敏感性分析

图8 显示了对氨-氢混合物点火延迟时间进行的归一化敏感性分析（各基元反应具体信息见附录A）。实验条件为：初始压力和温度分别为69.08 atm和1 500 K，添加的氨气浓度分别为5%、10%和15%。基元反应R1 和R13 对温度的敏感性最为显著，它们在整体反应中起主导作用。其中，基元反应R1 在燃烧过程中扮演了重要的推动反应，推动燃烧向高温方向发展。而基元反应R13 则是重要的抑制反应，限制了燃烧向高温方向发展。此外，基元反应R1、R3、R4、R13、R14、R15 和R17 的敏感性系数随氨气浓度的增加而降低。然而，氨气的添加却促进了基元反应R21 和R23 对温度的敏感性，其中，R21 促进了反应的进行，而R23 则抑制了反应的进行。因此，增加氨气浓度导致点火延迟时间增加。需要注意的是，基元反应R21 表明在氨-氢混合燃料中，NH3的分解产生了H2，而H2的生成又促进了氨-氢混合物的燃烧。

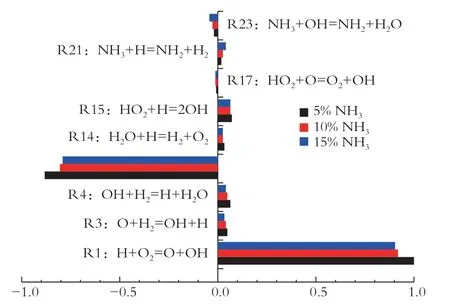
图8 归一化的不同基元反应的敏感性系数

2 CFD 模型验证

2.1 边界条件和网格无关性验证

本研究采用高压气体泄漏自燃的CFD 模型来验证氨-氢简化机理［51-54］，所建物理模型如图9 所示。在左侧高压区域，氨-氢按一定比例预混。计算域为5 mm×900 mm 的矩形管。计算区域的左边界为定义为压力入口边界条件。管道末端定义为压力出口边界条件。爆破片将高压区与低压区隔离开来。无论打开过程如何，爆破片都被认为是瞬间破裂。高压储罐和管道的壁面定义为绝热壁面边界条件。

图9 物理模型示意

为确保数值模拟结果的准确性，本研究进行了网格无关性验证。如图10 所示，在爆破压力为69.08 atm 时，对比了3 种网格数（13 264 个、14 480 个和16 064 个）下的管内最高温度随时间的变化。结果表明，13 264 个网格数的模拟结果误差较大，14 480 个网格数和16 064 个网格数的模拟结果误差较小，管内最高温度曲线基本重合。因此，本研究中CFD 模型使用的网格数为14 480 个。

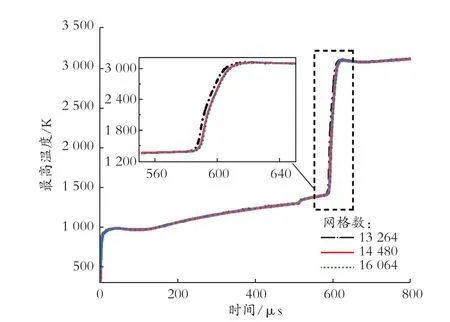
图10 网格独立性验证

2.2 简化机理的CFD 验证

本研究将简化的氨-氢混合燃烧爆炸机理与CFD 模型耦合，并与详细机理进行对比的效果。采用了ANSYS FLUENT 19.0 软件作为计算引擎，并使用基于控制体积的有限体积法进行求解。在求解过程中，选择双精度、基于压力的求解器，采用二阶迎风格式以提高计算精度。为处理湍流-化学相互作用并进行燃烧计算，采用RNG k-ε 湍流模型（基于雷诺平均Navier-Stokes 方程的用于模拟湍流流动的计算模型，适用于各种复杂流体流动和湍流强度较高的情况）、EDC（Eddy Dissipation Concept，涡流耗散概念）燃烧模型以及提出的氨-氢简化机理。为减少计算时间，采用原位自适应建表（ISAT）算法［52］进行数值积分。同时，考虑到链式反应的化学反应速率差异较大，本研究采用刚性化学求解器以提高化学反应计算的稳定性和收敛性。使用PISO 算法进行压力-速度耦合。在模拟过程中，采用时间步长为10-9s 的瞬态求解。并假设爆破片瞬间破裂，混合气体被定义为理想气体。最后将简化机理和详细机理分别耦合到之前建立的高压氨-氢泄漏自燃CFD 模型中。

为了验证数值模拟的准确性，Xu 等［53］的高压氢气泄漏自燃实验被选中来验证CFD 模型的合理性和准确性。在模拟中，CFD 模型选择与实验相同的条件和参数。实验结果与仿真结果对比如图11 所示，对比了爆破压力为59.61 atm 和69.77 atm 条件下，简化机理、详细机理和实验的平均激波速度。

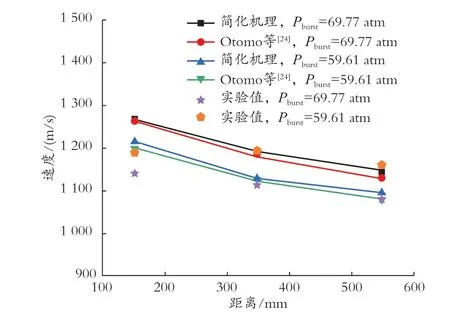
图11 简化机理与详细机理平均激波对比

从图中可以观察到，简化机理和详细机理的仿真结果均与实验数据吻合较好。在实际过程中，较高的释放压力（Pburst=69.77 atm）下爆破片的多级破裂过程中产生的压缩波叠加现象更为明显，这将增大了激波传播速度［54-56］。爆破片破裂结束后，由于流体黏性、管壁摩擦等能量耗散作用，激波会稳定地衰减，激波传播速度也会随之下降［53,57］。因此，在实验过程中，激波传播速度先增加后缓慢下降。由于简化机理去除了一些反应，使得平均激波速度稍大，更符合氢气燃烧的特性。在爆破压力为59.61 atm 下，与详细机理的最大相对误差仅为1.55%，平均相对误差为1.37%；在爆破压力为69.77 atm 下，最大相对误差仅为1.40%，平均相对误差为1.16%。综上所述，简化机理的可靠性得到了验证，这将大幅缩短氨-氢CFD 燃烧模拟的计算需求。

3 结论

本研究通过应用DRGEPSA 法成功简化了Otomo等［24］提出的详细氨氢燃烧爆炸机理。简化过程不仅保留了原始机理的核心特征，同时显著提高了计算效率，使得该机理更适用于实际工业应用。简化后的机理在预测氨-氢混合物的燃烧和爆炸特性方面显示出良好的准确性和可靠性，对于分析和优化氨-氢能源的储运及利用过程至关重要，特别是在安全性评估方面，为快速评估氨-氢能源系统的安全风险提供了有效的工具。此外，本研究也为无碳燃烧技术的发展提供了参考。简化机理有利于优化燃烧过程，实现更高的能量效率和更低的有害排放。本文也将简化机理的预测结果与实验数据和其他研究者的模拟值进行了比较，重点关注点火延迟时间和层流火焰速度。得出以下结论：

（1）在压力为1 ～ 30 atm，温度为298 ～ 2 500 K，当量比为0.5 ～ 2.0 时，简化机理在点火延迟和层流火焰速度计算方面与详细机理和实验数据吻合较好，具有良好的性能。模型验证了简化机理的可靠性。

（2）在H2占比较小时（摩尔分数小于0.2），详细机理更符合实验数据。在高H2摩尔分数的区域，简化机理与实验数据的吻合程度更好。这表明本研究中建立的氨-氢燃烧简化机理比Otomo 等［24］的详细机理更适合高氢气含量的工况。

（3）基元反应R1、R3、R4、R13、R14、R15和R17（详细反应方程见附录A，下同）的敏感性系数随氨添加浓度的增加而降低；基元反应R21 和R23 的敏感性系数随氨添加浓度的增加而升高。在氨-氢混合燃料中，基元反应R21 表明NH3分解形成H2，而H2的形成促进了氨-氢混合气体的进一步燃烧。

（4）通过分别耦合简化机理和详细机理的高压氨-氢泄漏自燃CFD 模型，在爆破压力为59.61 atm和69.77 atm 条件下，简化机理和详细机理的平均激波速度变化趋势一致，均十分接近实验数据，但简化后的机理大大缩短了氨-氢CFD 燃烧模拟的计算需求，这表明在模拟方面，简化机理更加适合氨-氢混合气燃烧。