基于正交试验的土体动力等效线性模型参数敏感性分析

张富有,葛 凯,周强强,魏宇辰

(1.河海大学 土木与交通学院,江苏 南京 210024;2.中建中环生态环保科技有限公司,江苏 苏州 215000)

土体力学性质的研究在岩土工程领域具有重要意义,对于确保工程结构的安全性和可靠性至关重要。其中土体本构模型参数的敏感性分析是保证工程分析准确性的关键步骤。过去的研究主要集中在土体静力本构模型参数的敏感性分析上,而对土体动力本构模型参数的深入研究相对较少。在岩土工程静力分析中,邓肯-张模型是最常用的本构模型之一[1-2],前人对其参数敏感性已有较多的研究。李炎隆等[3]基于正交试验法对混凝土面板坝坝体的竖向位移和水平位移进行了邓肯-张E-B模型参数的敏感性分析,结果表明参数Kb、φ0、K、Rf对坝体变形计算结果影响显著,而参数m、n、Δφ对计算结果影响较小。陈斌等[4]通过分解应力球量与应力偏量,导出了位移对参数偏导数的计算公式,并通过算例得出参数的敏感性与位移值的变化趋势相似的结论,且内粘聚力c敏感性最大,弹性模量系数K、破坏比Rf和内摩擦角φ也较敏感;而后又在文献[5]通过算例分析指出邓肯-张E-B模型参数对位移的敏感性除了考虑几何效应外,还应考虑荷载效应和自身取值效应的影响。邓成发等[6]研究了邓肯-张E-υ模型参数对基坑支护结构变形的敏感性,表明影响基坑支护结构变形的主要参数为K、G、Rf和n。在弹塑性模型方面,范益群等[7]为研究弹塑性模型参数的位移敏感度,以Drucker-Prager准则为例将应力球量与应力偏量进行分解,导出一个有限元计算中位移对参数灵敏度的闭合形式公式。

在动力反应分析中,土体的动力模型目前常用的主要包括基于粘弹性理论[8]的等效线性模型和基于弹塑性理论[9-11]的非线性模型两种。等效线性方法通过不断迭代来近似地反映土体的非线性,不仅计算效率高、而且适用于大多数情况[12-13]。在进行动力模型参数敏感性分析时,通常需要同时考虑多个试验因素,传统的参数敏感性分析方法只能考虑单因素对基准指标值的影响[3],若进行全面试验,则试验的规模将很大,而正交试验则利用正交表选出最优水平组合进行分析,极大地减小了工作量。

堰塞坝坝体由滑坡体形成,其本身材料具有大粒径、宽级配、不均匀性等特点,动力参数存在一定的不确定性。因此本文以某堰塞坝为例,坝体和坝基材料静力模型采用邓肯E-B模型,动力模型采用等效线性模型,基于正交试验法,对堰塞坝坝体竖向地震峰值加速度和竖向永久变形进行等效线性模型参数的敏感性分析,这一研究旨在为土体等效线性模型参数的选取提供有针对性的参考,特别是在考虑动力因素不确定的情况下,对于提高工程分析的准确性和可靠性具有重要意义。

1 等效线性模型

土体等效线性模型[14]由于计算效率高,在动力计算中广泛运用。它是由粘弹性理论发展而来,通过反复迭代计算近似反应土体的动力特性,其应力应变关系[13]为

τ=Gγ+ηGγ

(1)

式中,G为剪切模量,kPa;τ为剪应力,kPa;γ为剪应变;ηG为剪切粘滞系数,按下式计算:

ηG=2Gλ/ω

(2)

式中,ω为圆频率,rad/s;G和λ分别为土体的剪切模量和阻尼比,可以采用沈珠江[15]提出的以下公式进行计算:

(3)

(4)

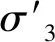
(5)

2 永久变形计算

对土石坝的永久变形,可以采用残余应变势模型计算。该方法通过静力计算得到九个应力分量以及动力计算得到最大动剪切应变,结合动三轴试验所得的残余应变结果,最终得到残余应变列向量。本文采用沈珠江模型[13,15]计算土石料残余体积应变增量Δεv及残余剪切应变增量Δγ,公式如下:

(6)

(7)

式中,N和ΔN分别为总振动次数与其时段增量;c1、c2、c3、c4和c5为5个试验参数。

3 等效线性模型参数的敏感性分析

以世界上首座堰塞坝综合水利枢纽工程为例,堰塞坝最大坝高169 m,坝长601.2 m。上下游蓄水高度分别为133.7和49.3 m,混凝土防渗墙贯穿坝身到坝底。堰塞坝是由滑坡体改造而成,因此考虑坝体为一次性形成,不进行坝体分步填筑模拟。上游分4步蓄水至坝顶,坝体分区由堰塞体1、堰塞体2、滑坡体、河床1、河床2组成。坝体横断面如图1所示,邓肯-张E-B模型材料参数、等效线性模型参数以及残余变形参数如表1、表2和表3所示。坝底为岩土层,防渗墙采用混凝土材料,两者浮密度均为1.5 g/cm3,弹性模量分别为6.0和28 GPa,泊松比分别为0.3和0.2。

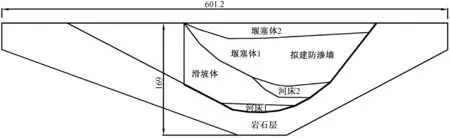
图1 坝体横断面(单位:m)

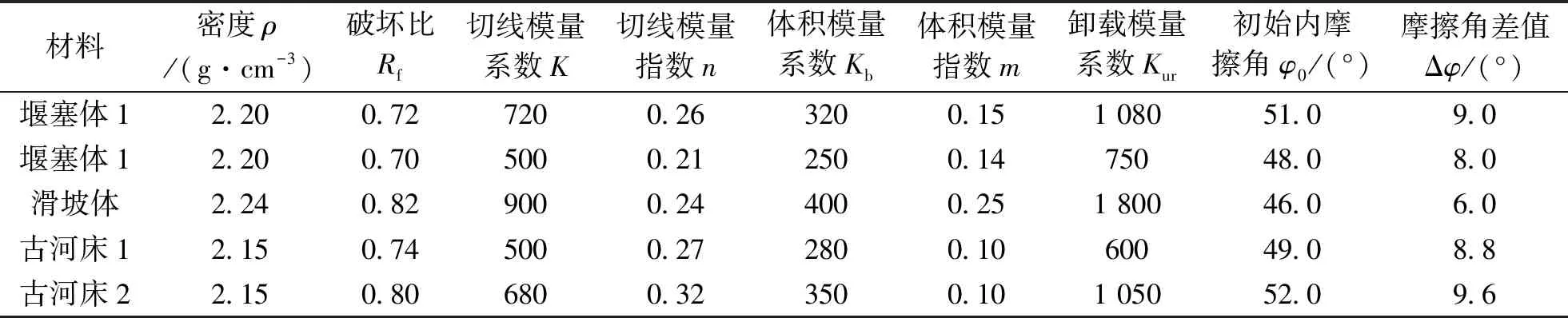
表1 邓肯-张E-B模型材料参数

表2 等效线性模型材料参数

表3 残余变形材料参数

工程区抗震设防烈度7度,且用于地震动力计算的地震波从岩石层底部输入,同时考虑顺河向、横河向和竖向三向输入,其加速度时程曲线如图2所示。

图2 地震加速度时程曲线

3.1 计算模型

采用8节点6面体单元对堰塞坝模型进行网格划分,共划分为89 862个单元,67 498个节点,堰塞坝坝体网格划分如图3所示。混凝土防渗墙与坝体之间刚度差异显著,通过设置接触面进行接触分析,实现防渗墙网格精细化划分。堰塞坝坝体分区如图4所示。

图3 堰塞坝坝体网格划分图

图4 堰塞坝坝体分区图

3.2 正交试验设计

正交试验是利用正交表来安排和分析多因素试验的设计方法,在工程中应用广泛[16-19]。选取坝体竖向峰值加速度和竖向永久变形作为试验指标,对等效线性模型中的k1、k2、n、v、λmax5个参数进行敏感性分析,并将坝体中的滑坡体作为正交试验分析的研究对象。以设计工况下(试验水平2)的材料参数为基础,将试验水平2的材料参数(因素)向下浮动20%作为试验水平1,向上浮动20%作为试验水平3,总计3个试验水平。具体试验参数及其对应的因素水平取值见表4。表4中共5个试验因素,3水平试验,如将全部水平进行组合,共有243种试验方案;若进行全面实验工作量大,耗费时间长,因此本文设计了16种正交试验,将实验因素的取值随机分配到正交表中,以此来模拟全面实验。

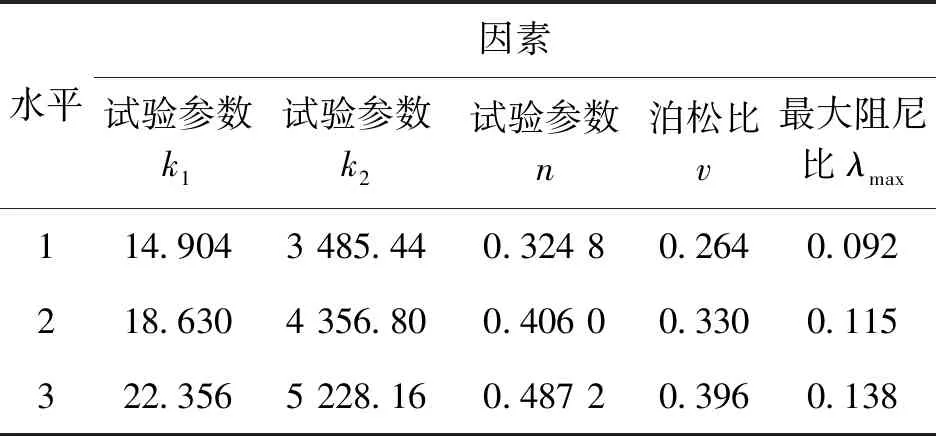
表4 正交试验因素水平取值

3.3 试验结果分析

正交试验的具体方案如表5所示,表中的每一行代表一个试验方案,从A1到A16共16种试验方案;表中的1、2、3分别代表表4中各参数的3种取值方案。对各方案进行三维动力分析,整理考核指标坝体的最大加速度和竖向永久变形的计算结果,如表5所示。表中显示,方案A13坝体的加速度峰值最小,为2.54 m/s2;方案A10坝体的加速度峰值最大,为4.80 m/s2;方案A15坝体的竖向永久变形最小,为45.1 cm;方案A9坝体的竖向永久变形最大,为47.34 cm。将峰值加速度最大的方案A10坝体最大纵断面的竖向地震峰值加速度和横断面的永久变形等值线画出,如图5和图6所示,图中显示,最大纵断面坝体竖向峰值加速度最大值为4.8 m/s2,最大永久变形为46.27 cm,坝体加速度的分布规律符合一般土石坝的加速度反应规律。

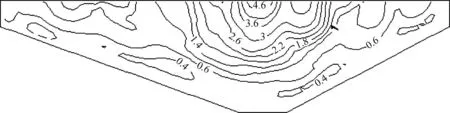
图5 竖向峰值加速度(单位:m/s2)

图6 竖向永久变形(单位:m)

表5 正交试验方案及试验结果

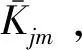
表6 竖向加速度峰值影响因素极差分析结果

表7 竖向永久变形影响因素极差分析结果

图7 堰塞坝各试验指标参数敏感性对比结果

4 结论

本文以堰塞坝为例,基于正交试验法研究了土体动力等效线性模型参数的敏感性,计算结果表明动力模型中参数k2、n、λmax对于堰塞坝坝体的地震反应影响较大,其中k2影响最为显著,k1、v对堰塞坝的地震响应影响较小;参数k2、k1、λmax对坝体竖向永久变形的影响较大,其中k2影响同样最为显著,n、v对竖向永久变形影响较小,以上结论可为土体动力本构模型参数的选取提供参考。