塑性混凝土咬合桩防渗墙变形机理研究

梁 超,李 斌,刘 润,朱 楠,李青欣

(1.天津大学 水利工程智能建设与运维全国重点实验室,天津 300072;2.港口岩土工程技术交通行业重点实验室,天津 300222;3.中交第一航务工程局有限公司,天津 300461;4.中交天津港湾工程研究院有限公司,天津 300222;5.天津市港口岩土工程技术重点实验室,天津 300222)

咬合桩是桩与桩之间有部分重合交错,形成一排钢筋混凝土与素混凝土交叉排列的桩墙围护结构。咬合桩采用“荤桩”与“素桩”搭配使用,能够起到良好的止水作用,相比于地下连续墙节约了大量的材料成本和施工工期,具有较强的工程应用前景[1-3]。国外对钻孔咬合桩支护结构的研究和应用较早,在变形计算、基坑监测以及变形约束措施上都有相关研究。Bryson等[4-6]介绍了钻孔咬合桩在美国芝加哥地铁车站的地下支护方案。Di等[7-8]介绍了钻孔咬合桩作为止水帷幕,作用在美国的Walter F. George蓄水坝的防渗工程中,取得了良好的止水效果。Tony[9]提出对钻孔咬合桩不仅要注重素混凝土桩28天强度,还要注重7天强度,应在2～7 MPa之间。

钻孔咬合桩这种新工法支护结构在我国出现较晚,最早的应用是在深圳地铁的隧道工程中。王安龙[10]、张中安[11]以深圳地铁隧道明挖段的深基坑支护工程为实例,对咬合桩的设计方法以及施工方案等内容进行研究,提出施工顺序、施工精度等对于工程质量的影响和相应解决办法。近些年来,随着钻孔咬合桩在工程中的成功应用,吸引了大量的学者对其进行探索和研究。范恒秀等[12-13]根据杭州地铁秋涛路站咬合桩的使用情况,提出了套管钻机加旋挖钻机配合钻孔咬合桩成孔的方法,并对咬合桩超深钻进时桩体垂直精度的控制问题提出了解决办法。康涛等[14]讨论了某市轨道交通线车站基坑开挖咬合桩围护工程,咬合桩围护采用全荤桩的搭配形式,提出了解决矩形钢筋笼在起套管时被带扭曲这一问题的解决办法。杨建学等[15]以福建某基坑工程为研究对象,研究了在临海条件地层下咬合桩的围护效果。秦东平等[16]以北京地铁某线暗挖隧道工程为例,探究了咬合桩作为止水帷幕的施工优化方法。张晓涛等[17]通过数值分析方法研究了咬合桩直径、桩间距变化对围护结构、基坑及地表最大位移变形的影响。李恒等[18]通过室内试验研究了咬合桩桩长对抗弯性能的影响。

综上所述,国内对咬合桩施工工艺、现场支护效果检测和桩基材料性能方面进行了广泛研究,但对咬合桩的工作机制和变形机理尚缺乏系统研究,尤其是塑性混凝土咬合桩作为防渗结构的研究中缺乏土压力和水头荷载作用下的受力变形研究,因此本文结合大连湾沉管隧道工程基坑止水帷幕监测数据,采用数值分析手段,开展塑性混凝土咬合桩受力机制和变形机理研究,明确了关键影响因素,为咬合桩的设计和应用提供理论基础。

1 数值模型建立及验证

1.1 工程概况

大连湾海底隧道建设工程在南岸设置接岸段,南岸工程深基坑分为港池部分和陆域部分,其中港池部分平面布置如图1所示,港池深基坑围堰止水采用了塑性混凝土防渗墙,本文以3#码头前设的斜坡式围堰为研究对象开展数值分析工作。围堰顶宽14 m,顶高程2.84 m,坡比为1∶1.5,围堰提心采用开山石碴回填,塑性混凝土咬合桩防渗墙距离3#码头前沿线6 m,咬合桩桩径1.0 m,咬合0.25 m。

图1 港池平面示意图

1.2 数值模型的建立与验证

1.2.1 模型建立

数值计算模型采用PLAXIS 3D有限元分析软件,模拟3#码头前沿临时围堰并分析塑性咬合桩防渗墙的工作性能,模型中对围堰结构进行了适当简化,主要包含咬合桩防渗墙、回填料及地基土,整体计算模型如图2所示。

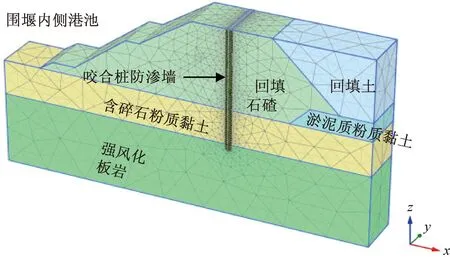
图2 计算模型示意图

模型中所有单元均为实体单元,土体遵循摩尔-库伦强度准则,塑性咬合桩采用弹性模型,模型x方向长60 m,y方向(咬合桩布置方向)长10 m,z方向长45 m。

1.2.2 模型参数

塑性防渗墙咬合桩结构桩长27.74 m,进入强风化板岩层2 m,围堰港池内水头高程-12.34 m,外侧水头高程-1.5 m,模型具体参数如表1所示,地基土体及回填料参数如表2所示。

表1 咬合桩材料参数

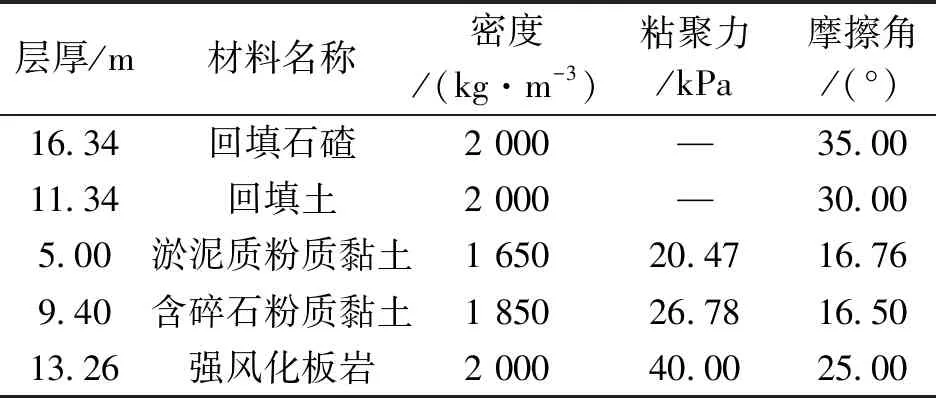
表2 土层及回填料参数

在实际工程中一般按等效抗弯刚度原则将咬合桩结构等效为一定厚度的地下连续墙来进行计算,此方法适用于咬合桩结构为有筋桩与无筋桩的搭配形式(图3),等效地下连续墙厚度h可根据截面等效抗弯刚度确定,如式(1)—式(4)所示。

图3 咬合桩结构的等效

咬合桩II序桩截面惯性矩为

(1)

等效地下连续墙矩形截面惯性矩为

(2)

按照等效抗弯刚度原则I1=I:

(3)

推导出:

(4)

式中,d为咬合桩直径,m;r为半径,m;t为相邻两荤桩间距,m;h为等效后的墙体厚度,m。

1.2.3 计算步骤

计算第一阶段建立初始地基土层,通过K0过程方式产生初始应力场,在该阶段所有的结构构件均处于冻结状态;第二阶段为建立3#码头围堰结构;第三阶段为浇筑咬合桩结构(咬合桩开始施工之前周边土体已在重力的作用下达到稳定状态,所以在模型中应该将前两阶段产生的位移重置为0);第四阶段为变化咬合桩防渗墙的两侧水头,分析咬合桩在水压力及土压力作用下的变形机制。

1.2.4 结果分析

在咬合桩防渗墙结构施工之前,周边土体已在自重作用下趋于稳定,故只对结构在第三阶段以后发生的位移进行分析。为更直观地观察咬合桩结构的侧向位移及水头在桩身上的分布情况,提取其位移云图及两侧水头变化云图如图4和图5所示。

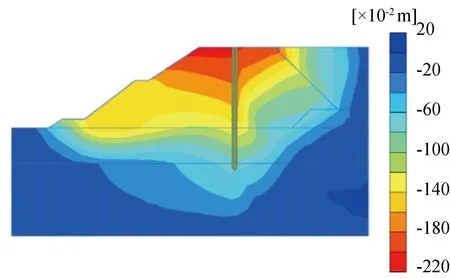
图4 水平向位移分布

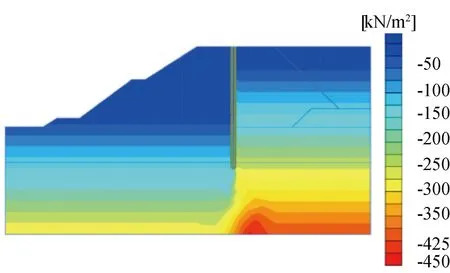
图5 孔隙水压力分布

结合图4可以看出,整个土体有发生滑坡的趋势,坡顶处土体的水平向位移最大,坡脚处土体的水平向位移较小。从图5可以看出咬合桩的防渗作用较为明显,由于桩身嵌固进入强风化板岩2 m,阻断了两侧土体渗流的发生,有效地避免了防渗桩左侧水位的抬升。与此同时由于两侧始终存在的水头差,导致桩身始终受水平力作用。为更好地观察桩身变形及应力变化,提取桩身的水平向变形及弯矩如图6和图7所示。

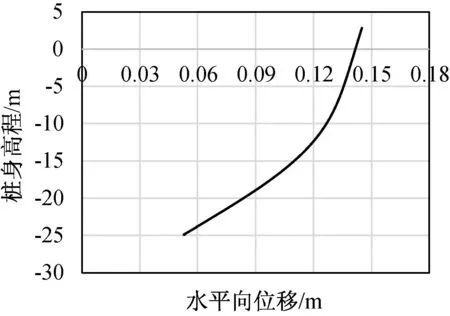
图6 桩身水平向位移分布

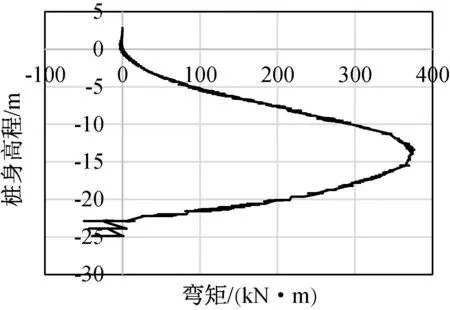
图7 桩身弯矩分布

如图6所示,在土压力及水压力的联合作用下,咬合桩发生指向围堰内侧水平向变形,且桩身变形呈现出桩顶位移最大,随着咬合桩埋深增大桩身变形逐渐减小的趋势。其中,由于强风化板岩其节理裂隙极发育,结构大部分破坏,岩芯破碎,部分石块手可折断,遇水易软化,对于嵌固在其中的桩体不能实现完全约束,因此即使桩身嵌固进入强风化岩石中2 m,仍然会发生一定程度的位移。图7中,桩身弯矩在高程为-13 m时,即约桩身1/2位置处取得最大值为376 kN·m。当咬合桩埋入强风化板岩后,桩身弯矩表现为与上部桩身相反的方向,为负值。

3#码头围堰分别布置了止水墙水平位移监测点及坡顶水平位移监测点,将计算结果与监测数据进行对比,如图8所示。

图8 数值结果与实测数据对比

数值模拟所得围堰坡顶的水平向位移为151 mm,与实测数据所得的169 mm相差为10.7%。数值模拟计算得到止水墙顶的水平向位移为145 mm,与实测数据所得的149 mm相差为2.7%。且实测数据可反映止水墙顶的水平向位移小于围堰坡顶水平向位移的规律,验证了本文模型计算的可靠性。

2 咬合桩变形特性分析

水头及土压力的耦合作用会导致咬合桩及其内、外侧土体发生不同情况的位移,若不加以控制会严重影响整体结构安全,因此需对咬合桩变形机理进行分析,明确其变形控制的关键影响因素。基于以上问题开展不同因素对塑性混凝土咬合桩防渗墙结构水平位移及桩身弯矩的影响研究。

2.1 土压力对咬合桩变形的影响

基于上述有限元方法建立模型将防渗墙两侧的水头差调整为0,从而达到咬合桩仅受土压力作用的目的。为探究土压力作用下咬合桩的变形机理及整体结构的变形发展模式,提取整个断面的总位移云图及水平向位移云图,如图9所示。

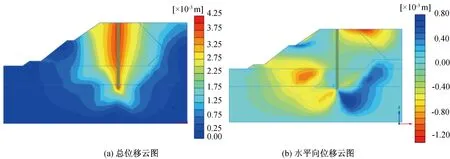
图9 位移分布

为了更好地观察桩身变形及应力变化,提取桩身的水平向变形及弯矩变化如图10和图11所示。

图10 桩身水平向位移分布

图11 桩身弯矩分布

由图10和图11可知,当仅有土压力作用时,桩身最大水平向位移为0.6 mm,正向最大弯矩为3.83 kN·m,负向最大弯矩为-2.89 kN·m,整个桩身几乎未发生变形。此时桩侧的主被动土压力较小,且嵌固入岩石的2 m长桩身对整个桩身提供了一个固定约束,致使整个桩身的位移被控制在1 mm的范围内。

2.2 水压力对咬合桩的影响

在上述模型的基础上将防渗墙两侧的土体调整为一类土体,同时两侧土体表面位于同一高程,恢复咬合桩两侧水头差,从而达到咬合桩仅受水压力作用的目的,提取咬合桩两侧土体的孔隙水压力和水平位移分布云图,如图12、图13所示。

图12 孔隙水压力分布

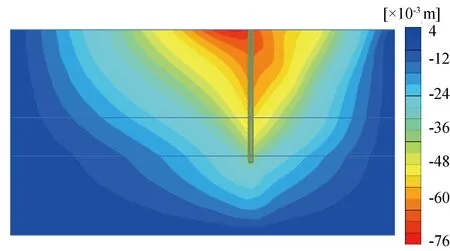
图13 水平向位移分布

从图12、图13中可以看出,咬合桩存在水头差,即咬合桩由于受到水头差导致的水压力作用进而产生水平向的附加位移变形,为探究在水压力作用下咬合桩的变形机理及整体结构的变形发展模式,提取桩身的水平向位移及弯矩变化曲线如图14、图15所示。

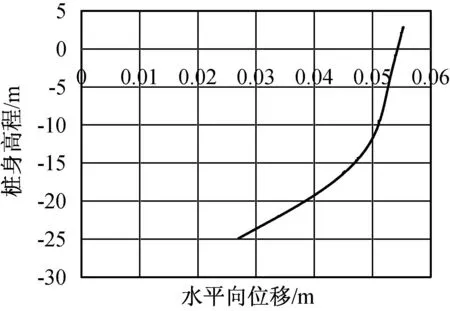
图14 桩身水平向位移分布(单水头差)

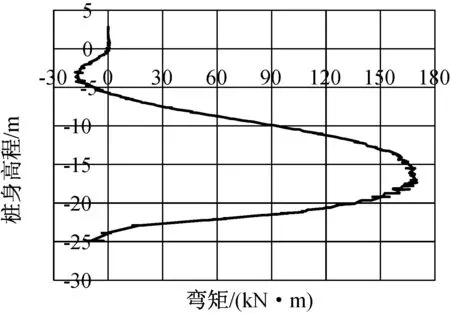
图15 弯矩分布(单水头差)

如图14、图15所示,当仅有水压力作用时,桩身最大的水平向位移位于桩头位置处,为0.055 m,桩身正向最大弯矩为170 kN·m,负向最大弯矩为-18.2 kN·m。相比土压力单独作用的情况,水压力单独作用下桩身产生更大水平向变形,桩身的弯矩也更大。将土压力、水压力单独作用工况与土压力、水压力共同作用工况进行对比,如图16及图17所示。

图16 咬合桩水平向位移分布

图17 咬合桩弯矩分布

从图16和图17可以看出,当土压力与水压力共同作用时,桩身位移和弯矩最大且二者的共同作用效果大于土压力、水压力单独作用时的桩身位移之和。产生这种现象的原因是当水压力与土压力共同作用时,由于左侧填筑形成的斜坡状围堰,导致咬合桩左右两侧受到的土压力大小不一致,土体对于咬合桩左侧的约束作用较弱,此时在指向左侧的水压力作用下桩身产生更大的变形。与之相对应,土坡整体也产生较大的位移。与此同时,当土压力与水压力共同作用时,桩身弯矩最大值为367 kN·m,大于土压力、水压力单独作用时的桩身最大弯矩之和。

综上可知,水压力对于桩身的变形起主导作用。然而当同一方向的土压力与水压力共同作用在咬合桩上时,土压力会加强水压力的作用效果,使包括桩结构在内的整个土体产生更大的变形及弯矩。

2.3 水头变化的影响

为研究水头对咬合桩变形的影响,建立水头差分别为6.0、8.0、10.0、12.0及14.0 m的模型进行计算,以水头差8和12 m为例给出了整体水平向位移分布情况,如图18所示。

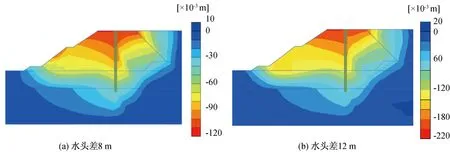
图18 不同水头下的土体位移云图

图18结果显示,不同水头差作用下,咬合桩及土体的水平向位移均在围堰坡顶处达到水平向位移最大值,在水压力及土压力的耦合作用下,土体内部形成近似贯穿多个土层的滑裂面。随着水头差的增大,咬合桩及土体的位移幅值逐渐增加。为定量地比较不同水压力作用下桩身的水平向位移及弯矩的发展规律,提取桩身水平向位移及弯矩变化曲线如图19和图20所示。

图19 不同水头下咬合桩水平向位移分布

图20 不同水头下咬合桩弯矩分布

从图19和图20结果可以看出,水头差与咬合桩结构的水平位移及桩身最大弯矩成正比,且随着水头差增大,桩顶相对于桩底的位移量也逐渐增大。当两侧水头差为10 m时,咬合桩顶部的最大水平位移值为0.124 m,桩身最大弯矩为346 kN·m;两侧水头差为6 m时,咬合桩顶部的最大水平位移值为0.06 m,桩身最大弯矩为204 kN·m,与水头差为10 m相比分别降低了51.6%及41.0%;两侧水头差为14 m时,咬合桩顶部的最大水平位移值为0.162 m。通过数据对比可以发现,咬合桩两侧水位的变化对咬合桩结构水平位移以及桩身弯矩的影响较大,当两侧水位相差较大时,咬合桩结构的变形会更加明显,对围堰土体的扰动也会相应增加。

2.4 土体坡度的影响

为研究土体坡度变化对咬合桩防渗结构变形的影响,建立土体坡度分别为1∶1.25、1∶1.5、1∶2、1∶2.5的模型进行计算。以1∶1.25和1∶2.5坡度为例给出了整体模型水平向位移分布,如图21所示。

图21 不同坡度下的土体位移云图

由图21可知,咬合桩左侧土体坡度不同时,整个断面的水平向位移云图基本一致,均在围堰坡顶处达到水平向位移最大值。在水压力及土压力的耦合作用下,土体内部形成贯穿多个土层的近似圆弧状的滑裂面。随着土体坡度逐渐变缓,可以明显看出围堰坡顶处的位移幅值随之逐渐减小。为定量比较不同土体坡度作用下桩身水平向位移及弯矩的发展规律,提取桩身水平向位移及弯矩变化曲线如图22和图23所示。

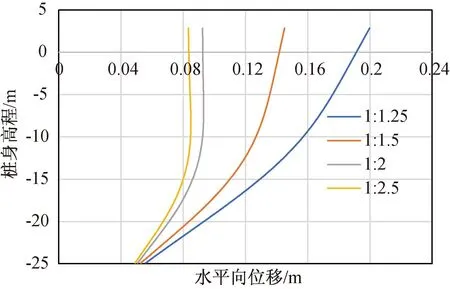
图22 不同土体坡度咬合桩水平向位移分布

图23 不同土体坡度下咬合桩弯矩分布

分析图22和图23的结果可知,当土体坡度为1∶1.25时,即咬合桩左侧内围堰坡度相对较陡时,桩身最大位移位于桩顶,为0.20 m,桩身弯矩为389.63 kN·m;当围堰坡度为1∶1.5时,桩身最大位移为0.15 m,桩身弯矩为376.46 kN·m;当围堰坡度为1∶2时,桩身最大位移为0.09 m,桩身弯矩为348.32 kN·m;当围堰坡度为1∶2.5时,桩身最大位移为0.08 m,桩身弯矩为325.30 kN·m。随着土体坡度的增大,桩身水平向位移及最大弯矩呈现出持续减小的趋势。当土体坡度小于1∶1.5时,在此范围内变化土体坡度对桩身水平向位移及弯矩的影响较小。当土体坡度由1∶1.5增大至1∶2时,可以看出此时桩身最大位移及弯矩均发生明显降低,且桩顶相对于桩底的位移也呈现减小的趋势。当土体坡度大于1∶2时,此时在土压力及水压力的作用下,桩身变形及弯矩分布较为相似。因此在进行咬合桩围护结构设计过程中,从围堰土体坡度这一角度出发,土体坡度应尽量放缓,不宜小于1∶1.5。

2.5 桩长的影响

在上述计算实例咬合桩原桩长的基础上增加4组桩长作为研究对象,具体计算工况如表3所示。

表3 不同桩长计算工况

以桩长16.34 m和27.74 m的计算工况为例,提取咬合桩及土体的水平向位移云图,如图24所示。

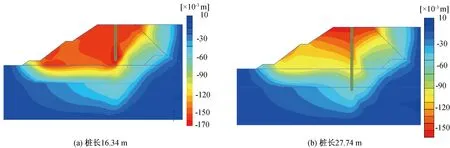
图24 不同桩长下土体位移云图

由图24可知,随桩长变化,咬合桩周围的土体变形及桩身应力变化有所差异。当桩长为16.34 m时,此时桩身未能嵌固在岩石中,桩体完全与回填石碴接触。在水压力及土压力的耦合作用下,桩身随着土体发生变形,土体形成完整连续的圆弧形滑裂面,此时桩身最大应力分布靠近桩底;随着桩长继续增大,当桩身嵌固在含碎石的粉质黏土或强风化板岩中时,有嵌固段的桩体土体中存在连续但不圆滑的滑裂面,桩身最大应力分布位于桩身约二分之一位置处。为定量比较不同桩长的咬合桩水平向位移及弯矩发展规律,提取桩身水平向位移及弯矩变化曲线如图25、图26所示。

图25 不同桩长下咬合桩水平向位移分布

图26 不同桩长下咬合桩弯矩分布

由图25和图26可知,当桩长较小未能嵌固在岩石中或嵌固深度较小时,此时桩身的水平向位移曲线存在明显差异。当桩长较小时,咬合桩随着土体产生变形,未能实现对于整体围堰结构的加强作用,此时桩结构的最大位移出现在桩底,桩长为16.34、18.34 m时最大位移分别为0.13、0.127 m,桩身弯矩曲线也较为类似,最大弯矩均出现在靠近桩底约四分之一位置处;当桩长增大出现嵌固段时,嵌固段的存在可充分发挥咬合桩对于结构的加强作用,桩身最大位移出现在桩顶位置处,当桩长为23.74、25.74及27.74 m时,桩身最大水平向位移分别为0.126、0.136及0.145 m,由于桩身长度的增大导致桩身挠度的增加,桩身最大变形随桩长增加而增大。

2.6 桩径的影响

桩径决定了咬合桩防渗墙桩身刚度,从而影响桩身变形的发展,为此建立不同桩径大小的咬合桩模型来分析桩径对咬合桩结构水平位移及桩身弯矩的影响,不同桩径计算工况见表4。

表4 不同桩径计算工况

以桩径800、1 200 mm的计算工况为例,提取咬合桩及土体位移云图,如图27所示。

图27 不同桩径下的土体位移云图

如图27所示,不同桩径下,土体断面变形较为类似,均在咬合桩左侧围堰坡顶处达到水平向位移的最大值,由于咬合桩的存在一定程度上限制了咬合桩右侧土体的变形,使得咬合桩右侧土体的水平向位移小于左侧水平向位移幅值,整个土体形成相对较连续的滑裂面。为定量比较不同桩径下的咬合桩水平向位移及桩身弯矩的发展规律,提取桩身水平向位移及弯矩变化曲线如图28、图29所示。

图28 不同桩径下咬合桩水平向位移分布

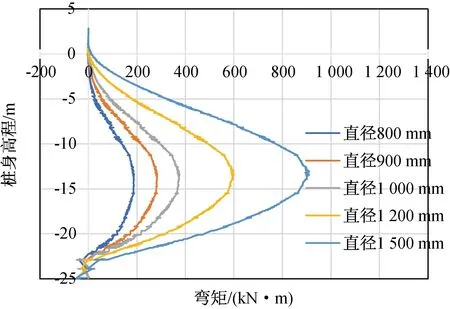
图29 不同桩径下咬合桩弯矩分布

由图28可以看出,随着桩径的增大,靠近桩顶约五分之一的桩身长度其水平向位移幅值逐渐增大,当桩径由800 mm增加至1 500 mm时,桩身处最大水平向位移由0.143 m增加至0.151 mm。其余部分桩身的水平向位移随着桩径增大呈现逐渐降低的趋势,从图中可以看出桩径对于桩身的水平向位移影响较小,当等效桩径增大83%时,桩身水平向位移变化仅为5.6%。如图29所示,随着桩径变化,桩身弯矩沿桩身分布规律较为一致,且均在桩身约二分之一位置处达到最大值,随着桩径增大,桩身弯矩由189 kN·m增大至910 kN·m。

3 结论

本项研究建立了分析塑性混凝土咬合桩防渗墙变形特性的三维数值计算模型,通过大连湾沉管隧道工程实测数据验证了数值模拟方法的正确性,并探究了咬合桩防渗墙变形特性随不同影响因素的演化规律,具体结论如下:

1)当土压力与水压力单独作用在咬合桩上时,水压力的作用更为显著,导致咬合桩产生更大的变形及内力。当水压力与土压力共同作用在咬合桩上时,水压力将占据主导地位,对咬合桩的变形及内力分布产生较大影响。

2)咬合桩两侧水头变化对咬合桩变形产生的影响较大,随着作用在咬合桩上水压力的增大,桩身变形及最大弯矩随之增大,对围堰土体的扰动也会相应增加。相比水头,土体坡度对桩身结构变形的影响较小,土体坡度越缓,桩身水平向位移及弯矩越小。对于一些深度大、对周边环境要求比较严格的围堰工程来讲,土体坡度应尽量放缓,建议不小于1∶1.5。

3)通过对桩身嵌固深度的研究,发现咬合桩桩长变化对其变形影响较大。当桩长较小桩身未能嵌固在岩石中时,在外部压力作用下,桩身随着土体发生变形,土体形成完整连续的滑裂面,随着桩长增加,桩身嵌固段加长,桩身最大位移出现在桩顶位置处,土体中存在连续但不圆滑的滑裂面,桩身最大应力位于桩身约二分之一位置处。随着桩径的增大,桩顶变形及桩身最大弯矩均呈现逐渐增大的趋势,弯矩沿桩身分布规律较为一致,且均在桩身约二分之一位置处达到最大值。