基于改进遗传算法的离场航班时刻优化
2024-03-09王大军
王大军
(兰州中川国际机场有限公司运行指挥中心, 兰州 730000)
现有的航班时刻安排往往只考虑一个小时内的航班量,而忽视了机场实际运行能力的多样性。因此现有的大多数航班时刻管理一般针对某一个整点小时内的航班容量进行约束,容易造成因航班时刻安排不均匀引起的某时间内航班密集,增加管制员的压力。例如,某机场在09:00—10:00的容量为28架次,但是在这个小时内,航班分布可能并不均匀。可能前半小时只有2架次的航班,而后半小时有26架次的航班量。虽然总航班数没有超过机场一个小时的运行容量,但这种安排明显不符合机场的实际运行能力,可能导致拥堵和效率低下。因此航班时刻的合理安排对于提高机场运行效率、降低空中和地面拥堵、保障航班安全具有重要意义。
从19世纪末开始,国内外学者就该问题展开研究。1993年,Abela等[1]引入人工智能算法,将航班排序与时刻问题视为0~1混合整数规划问题,并通过对20个架次的航空器数据进行验证。2006年,Aditya和Slater[2]提出了一种组合优化方法,用于改善进场航班时刻。2018年,Benlic[3]为了合理分配每个机场在机场网络中的航班时刻,开发了一种启发式算法,并通过不断迭代来优化航班时刻的分配结果。同时,国内学者也进行了相关研究,陈霞和陈浩文[4]基于单亲遗传算法(patheno-gentic algorithm,PGA)建立了以最小化航班延误总时间为目标的进场航班时刻优化模型,通过仿真计算验证其在延误时间方面远优于先到先服务。陈肯等[5]针对繁忙机场高峰时段的资源限制和不合理航班计划,引入基尼系数定义公平性,建立了航班时刻调整总量最小和各航空公司公平性最优的双目标优化数学模型。左杰俊等[6]考虑实际放行能力和航班调度难度,利用遗传算法建立了离场航班优化调度模型,并在上海虹桥国际机场验证。曾伟华等[7]从机场实际运行出发,利用航班优先级,构建航班时刻优化模型,旨在最小化航班请求时刻和分配时刻偏移量,通过增加机场进离港点容量约束,以上海浦东机场为案例验证。卢婷婷等[8]通过建立繁忙程度矩阵,并以最小化航班运行延误和减少目的地机场影响为总目标的航班时刻优化模型,结合粒子群算法,以武汉天河机场为例进行优化。方策[9]通过建立总延误成本最小的时刻优化模型,以京津冀机场群为例,通过改进后的匈牙利算法进行求解,运用 SIMMOD软件对优化后航班时刻进行仿真验证,通过对机场群航班时刻经过资源优化配置,减少了整体的航班延误。林雍雅[10]根据实际运行数据引入了进离场航班自跑道至共用航路点的飞行时间,提出了分级优化的求解方法为各方向航班分配优先级,并以京津冀机场群的日航班时刻为例,使用CPLEX软件进行算例研究,提出了以航班时刻序列为出发点建立机场群周航班时刻战略层优化模型。曾维理等[11]根据延误传播因果关系强弱来表征延误传播代价,建立了以最小延误传播代价和最大公平性的双目标函数,以上海浦东国际机场为例,从资源利用率和运行效率两方面进行了试验验证,证明优化后的航班时刻在时空分布上更加合理,能够显著提高资源利用率和航班正常率,降低航班延误。吕晨辉[12]通过对机场航班波特性分析、航班时刻分配影响因素和航班时刻市场分配效益三个关键问题展开研究,建立以净增效益最大为目标函数的运输机场增量航班时刻分配模型,使用TAAM (total airspace and airport modeller) 仿真软件进行实例验证,验证运输机场增量航班时刻分配最佳方案。
本文从机坪管制和合理安排离场航班时刻、提高航班放行正常率角度出发,在假设进场航班时刻不变的情况下对离场航班时刻进行优化研究。设计具有自适应交叉概率的遗传算法,采用航班时刻字符型自然数编码方法,对离场航班时刻数学模型进行智能优化,达到前后离场航班时刻调整时间偏差总量最小目标。通过仿真手段,对所提算法在航班时刻优化问题中的有效性和优越性进行验证。
1 问题描述
把时间分成5 min时间片段,并分别对连续15 min和60 min的机场容量进行了限制。主要目标是根据实际的运行保障能力来调整航班时刻。考虑了3个时间片的容量限制和调整量约束。在保持进场航班时刻不变的情况下,安排离场航班时刻和时间片内数量不会超过机场的实际运行容量以及前后离场航班时刻调整时间偏差总量最小,避免离场航班拥堵或跑道头等待,有效提高机场航班放行正常率。
2 模型建立
2.1 目标函数
以最小化离场航班时刻调整时间偏差总量为主要目标,建立以下目标函数:
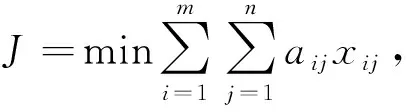
(1)
(2)
式中:aij为航班时刻调整量;xij为决策变量;m为待优化的航班数;n为可用的时刻数;以5 min为一个单位时刻。
2.2 约束条件
航班时刻受唯一性约束,每个航班有且仅有被分配的一个时刻。
(3)
在实际运用中,还应当考虑航空公司的经济利益,尽可能减少航班的时刻调整量。对航班时刻调整范围约束。
(4)
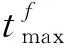
为了使结果符合实际运行情况,制定更加平滑和精细的航班计划,将以5 min作为时间片段,对任意连续时间片长度为5 min、15 min、60 min内的离场航班时刻容量进行限制。
(5)
(6)
(7)
式中:i=1,2,…m;j=1,2,…,n;C5 min、C15 min、C60 min分别为连续5 min、15 min、60 min的离场航班时刻容量值。
3 算法实现
3.1 算法改进
交叉概率pc和变异概率pm能够根据适应度自动调整。当种群各个体适应度趋于局部最优或者趋于一致时,使pc和pm增加; 而在种群适应度分散较大时,使pc和pm减小。同时,对于适应度高于群体平均适应值的个体,保持其在下一代中的存在; 而低于平均适应值的个体,对于较低的pc和pm,将其淘汰。
因此,自适应的pc和pm能够提供相对某个解的最佳pc和pm。自适应遗传算法在保持种群多样性的同时,保证遗传算法的收敛性。自适应遗传算法中,pc和pm按如下公式进行自适应调整:
(8)
(9)
式中:f′为要交叉两个个体中较大的那个的适应度值;favg为每代群体的平均适应度值;fmax为群体中最大的适应度值;f为要变异个体的适应度值。
3.2 算法设计
把问题的特征进行编码是设计遗传算法的首步,进行的编码方法需要能够表达问题的解。
在对本文问题的求解当中,为了降低算法数据操作维数和运算量,将对航班时刻的编码转化为对航班序号的编码操作。每个航班的允许调整时刻受可接受最大时刻调整量限制。取原有航班时刻为基准0,对该最大时刻调整量限制范围内的有效航班时刻以5 min时间片段间隔进行时刻偏移量的整数序列编码,就产生一个具有正负符号的维数较小的时刻偏移量编码序列。每个航班的航班时刻偏移量时间片段倍乘因子,从该时刻偏移量编码序列中随机选取,建立航班与时刻偏移量倍乘因子间的一一对应关系。
一个染色体的基因位置顺序号固定不变对应原始时刻表中全体离场航班顺序号。基因位置顺序号对应着原始航班时刻并作为基准0时刻。该染色体的基因值也取为离场航班序号。对染色体基因值的遗传编码操作,映射为对时刻偏移量倍乘因子的操作。根据染色体基因位置顺序号与其对应的基因值间的关系,计算离场航班的变动或优化时刻。
这种确定航班时刻的方法,大大降低了遗传编码数据的操作量和运算量。
(1)编码设计:采用随机正整数编码的方式对染色体进行编码。该编码方式使每个航班号对应一个染色体内的一个唯一的随机正整数。需要排序的航班数与编码长度一致。一条染色体刚好对应一个全体离场航班排列,数字的大小代表着航班的次序先后。
若有10架次航班需要排序,命名而F1~F10,则该编码方法在1~10随机生成10个整数按大小映射到航班序列上,生成了1条染色体:
航班序列:F9 F5 F1 F3 F7 F4 F2 F10 F8 F6
染色体: 9 5 1 3 7 4 2 10 8 6
(2)交叉运算:由于采用了正整数编码,在交叉运算当中不可避免地会产生无效解,故采用部分映射杂交方法,选择双交叉点进行染色体基因交换操作。下面将进行举例说明。
首先对种群中的染色体进行配对,每组将会有两个染色体进行两个交叉点的交换。如确定了以下父代染色体A和父代染色体B的两个交叉点位置,对交叉点内数据进行交叉操作。
父代染色体A:9 5 1 3 7 4 2 10 8 6
父代染色体B:10 5 4 6 3 8 7 2 1 9
则得到子代染色体A1和子代染色体B1。
子代染色体A1:9 5 16 3 82 10 8 6
子代染色体B1:10 5 43 7 47 2 1 9
交叉后,发现同一个个体出现重复数字现象,将导致出现无效解,对此,不重复数字将会被保留,冲突数字用*取代。
子代染色体A1:9 5 16 3 82 10 * *
子代染色体B1:10 5 *3 7 4* 2 1 9
采用部分映射的方法消除出现的冲突数字,根据父代染色体A和B,利用中间段的对应关系进行映射,得到:
子代染色体A1:9 5 16 3 82 10 4 7
子代染色体B1:10 5 83 7 46 2 1 9
(3)变异运算:采取随机抽取2个位置的基因片段进行互换操作。如随机选择父代染色体A的第4和第7个基因进行互换,结果如下。
父代染色体A正常状态:
父代染色体A:9 5 137 4210 8 6
变异后的子代染色体为
父代染色体A1:9 5 127 4310 8 6
3.3 算法流程
航班时刻优化的遗传算法流程如图1所示。
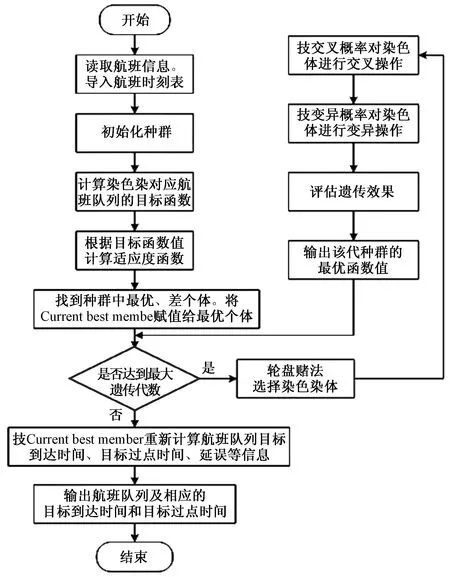
图1 航班时刻优化遗传算法求解流程
实现遗传算法的具体步骤如下。
步骤1:读取需要排序的航班信息。
步骤2:初始化种群。
步骤3:计算染色体对应航班队列的目标函数。根据染色体确定的航班序列,按间隔要求和约束条件计算计划过点时间以及延误值,将不满足最大允许位置交换约束的航班加10 000 s,计算目标函数值。直到计算出整体队列。
步骤4:根据目标函数计算适应度函数。
步骤5:找到种群最优和最差个体,最优个体赋值给Current best member。
步骤6:判断进化代数是否满足小于最大代数的条件。若满足,代数加1并按顺序执行,否则转到步骤13。
步骤7:轮盘赌选择。
步骤8:按自适应交叉概率对染色体进行交叉操作。
步骤9:按变异概率对染色体进行变异操作。
步骤10:依次执行步骤3、步骤4和步骤5。
步骤11:评估遗传效果,若当前最优个体优于Current best member,将其赋给Current best member,反之则被Current best member取代。
步骤12:输出这代种群平均和最优函数值。
步骤13:按Current best member重新计算航班队列的目标到达时间、目标过点时间、延误等信息。
步骤14:输出航班队列及相应的目标到达时间和目标过点时间。
4 实例与仿真验证
选取兰州中川国际机场某日455起降架次的历史进离场航班时刻表进行优化。其中进场航班230架次,离场航班225架次。
求解的遗传算法采用MATLAB编程语言编写程序。程序参数设置如下:种群规模为160,最大进化代数为200,变异概率为0.2,pc1=0.9,pc2=0.6,pm1=0.1,pm2=0.001。
根据兰州中川机场实际运行情况,机场离场小时容量为每小时21架次,15 min离场放行能力约8架次,5 min离场放行能力约4架次;C60 min=21,C15 min=8,C5 min=4。
同时,为了使调整后的时间具有普适性和实用性,优化的时间调整量范围限制设置为前后不超过15 min,换言之,如果某航班调整前的起飞时间为08:15,那个该航班优化后的时刻为08:00—08:30的一个合适的值。
对从历史航班时刻表中提取的离场航班时刻表使用本文算法进行优化。相对起始,优化后的离场航班时刻调整时间偏差总量共减少了268 min,减少了38.98%。优化调整的离场航班41个。求解时间为111.8 s,目标函数值从第32代收敛,历代目标函数值迭代曲线如图2所示,可以判断为得到本次运算优化解。算法收敛并有效。
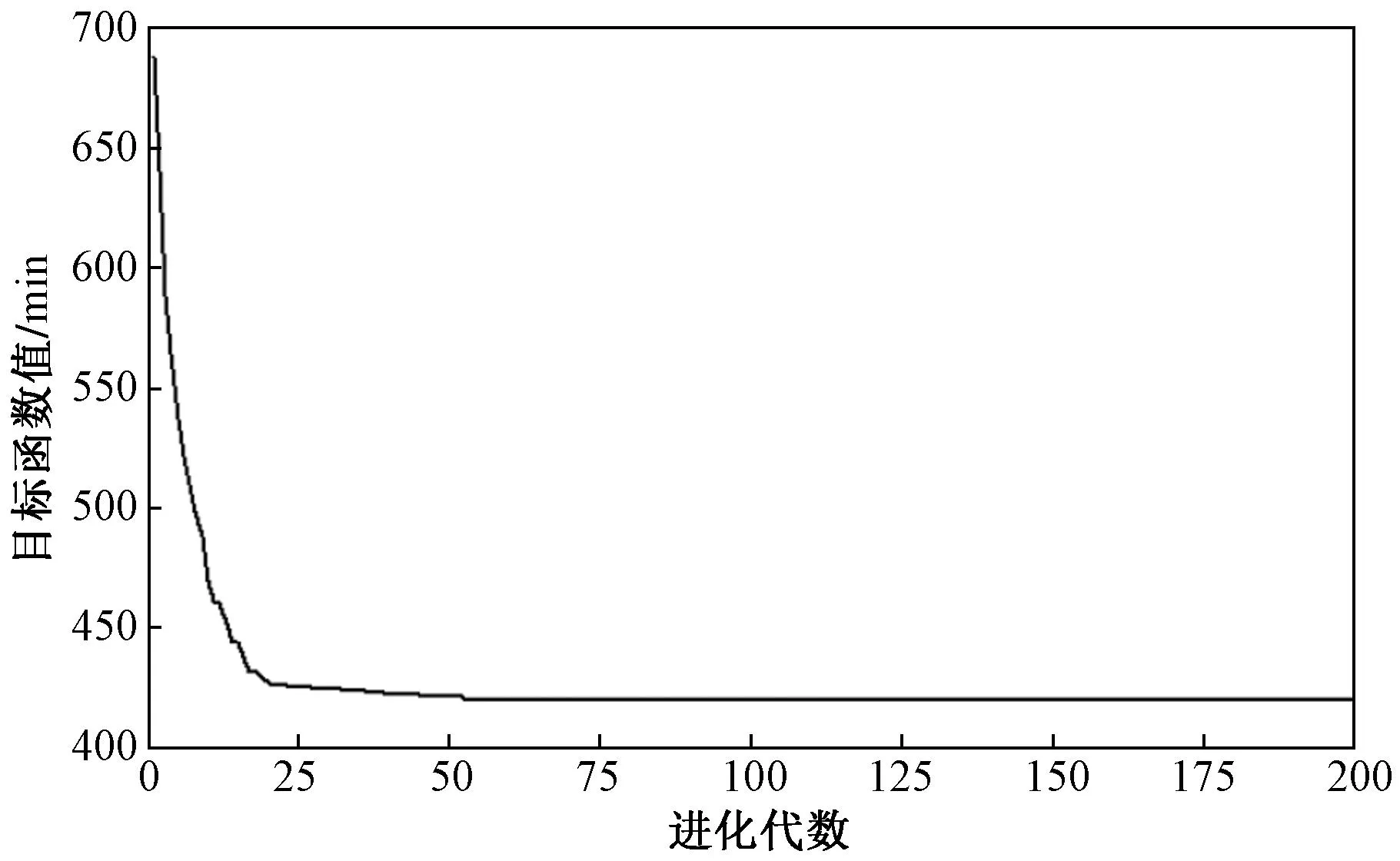
图2 历代目标函数值迭代曲线
依据优化后的离场航班时刻,替换原始历史进离场航班时刻表中离场航班时刻形成优化的进离场航班时刻表。将原始的和优化后的进离场航班时刻表分别导入已经建立的兰州中川机场的全空域和机场TAAM仿真模型,建立优化前后的两种仿真场景并分别进行运行仿真。兰州管制区和兰州机场仿真模型与仿真场景如图3和图4所示。
图3 兰州管制区3D仿真场景

图4 兰州机场3D仿真场景
仿真后分别获取两种场景的仿真数据库中航班仿真运行时间数据,分别计算两种场景下平均航班延误时间和航班放行正常率。优化前后两种场景下的结果比较如下表1所示。
由表1可知,优化离场航班时刻后,航班平均延误时间降低了1.04 min,达12.8%;离场航班平均延误时间降低了2.42 min,达22.3%;离场航班延误架次减少了27架次,达42.8%;航班放行正常率从72%提高到了84%,提高了12%。主要原因是由于优化了离场航班时刻,有效降低了跑道头的航班拥堵,减少了跑道头等待的离场航班架次和等待时间,从而提高了机场航班放行正常率。
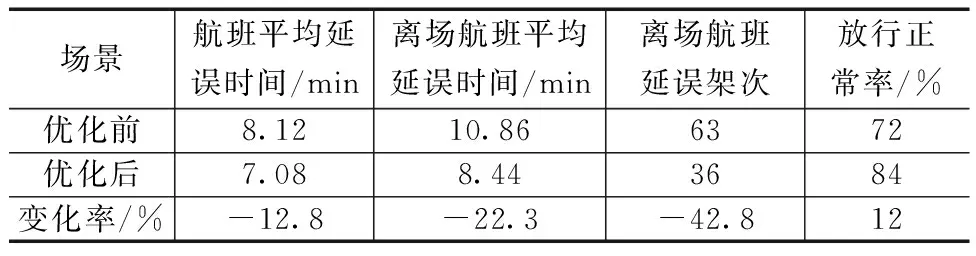
表1 优化前后仿真结果比较
5 结论
对机场离场航班时刻进行重新排序与优化,可以明显减少离场航班跑道头拥堵、等待离场航班数量和等待时间延误,提高机场航班放行正常率。采用基于自适应交叉概率的遗传算法可以有效优化离场航班时刻问题,得到合理的可行解,降低航班延误,提高航班放行正常率。基于自适应交叉概率的改进遗传算法能够为航班排序和时刻优化决策辅助系统开发和应用提供重要价值。未来的研究可以考虑扩大研究范围,涵盖更多的航班数,以更全面、准确地评估遗传算法在空中交通系统优化中的应用效果。
